加速度场下陀螺光纤环形变的影响分析

王斌华，黄迟航，胡 桥，孔 军，陈 平

（1.长安大学 道路施工技术与装备教育部重点实验室，陕西 西安 710064；2.西安交通大学 陕西省智能机器人重点实验室，陕西 西安 710049；3.西北工业大学 机电学院，陕西 西安 710072；4.中国航空工业集团公司 西安飞行自动控制研究所，陕西 西安 710065）

引言

光纤陀螺是用来检测运动角速度的理想传感器，已广泛应用于惯性导航系统、姿态稳定与控制系统等[1]。光纤陀螺需要保持高效性和可靠性，但在实际工作环境中，光纤陀螺与航天器载体固联，因此将直接承受航天器大机动运动时的加速度影响，作为光纤陀螺光学核心部件−光纤环，其折射率和偏振特性对外部和内部的结构应力荷载非常敏感，因此，在高动态环境下，研究大机动或强振动时直线加速度场对光纤陀螺的结构形变机理，是光纤陀螺精确定位并保持装备运行正常的关键，对提高输出精度具有显著意义。

许多研究者针对角加速度引起的误差进行建模和分析，利用信号处理软件实现了误差抑制。文献[2]提出了一种补偿光纤陀螺随机误差的滤波方法，能有效地去除光纤陀螺漂移噪声，提高光纤陀螺的测量准确度。文献[3]建立了闭环光纤陀螺的角速度误差模型，指出了影响光纤陀螺角加速度误差因素包括控制回路总增益及控制周期等，建议应结合系统对陀螺的测量精度要求配置合适增益参数，最后通过实验测试验证了该误差模型。文献[4]研究了振动影响下光纤陀螺干涉信号表现形式，为了提高光纤陀螺的稳定性和测量精度，通过改进信号调理方案有效抑制信号噪声和漂移。文献[5]建立了全数字闭环光纤陀螺动态模型，分析了光纤陀螺跨条纹工作机理和条件，提出了适应高频冲击环境的结构设计和软件优化方案。文献[6]基于自动控制原理和光纤陀螺闭环控制方案，指出角速度是导致摇摆误差的主要因素，并建立了光纤陀螺摇摆状态的简易模型，基于等效输入原理的动态测试方法针对不同摇摆频率进行了摇摆误差测试和补偿。零漂是衡量光纤陀螺精度的最重要、最基本的指标。学者们进行了有关陀螺零偏的研究。文献[7]推导出方波调制误差与陀螺零偏输出的关系，并经实验验证得出了陀螺内部电子元件间的电磁干扰是引起陀螺温度零偏变化的主要因素。文献[8]研究了温度和磁场对陀螺零偏误差的影响。文献[9]进行了在变温工况下陀螺输出及零偏不稳定性的实验研究，以解决陀螺的光路是否存在偏振串扰的问题。文献[10]建立了光纤陀螺随机漂移模型，通过滤波处理有效提升光纤陀螺的输出精度。另外，学者们发现陀螺输出角速度噪声特性中的随机游走性能是影响陀螺精度的主要因素，可从陀螺设计和工作参数设置方面改善游走性能，例如设定合适入射光功率和偏置工作点[11]。文献[12]研究了反馈延迟对光纤陀螺振动的影响，并对不同反馈延迟下光纤陀螺的跟踪性能以及输出进行仿真分析，实验对比研究表明减少反馈延迟可以改善振动环境下光纤陀螺的输出精度。文献[13]研究了光纤环的温度特性对光纤陀螺角速度误差和零偏稳定性的影响。

综上所述，角加速度是影响高精度光纤陀螺测试性能的客观因素，可以从信号处理、结构设计和工作参数设置等方面进行误差抑制。很多学者都从温漂误差处理和振动处理对光纤陀螺进行研究和改进。但是，实际航天器载体在大机动或者强振动的环境中，直线加速度场作用对光纤陀螺测试精度的影响研究较少。针对该问题，本文首先进行了正交各向异性结构的光纤环复合材料细观力学的代表性体积单元（RVE）的有限元分析，获得其等效材料参数以准确模拟光纤环形变，再建立了陀螺光纤环组件的空间有限元模型，分析了光纤环在不同加速度场作用下的变形结果，研究了直线加速度场下的光纤环形变机理，为改善光纤陀螺仪的结构稳定性、提高光纤陀螺仪的测量精度以及对后续高精度光纤陀螺研制提供指导。

1 光纤环组件结构和材料参数

1.1 结构组成

光纤环组件由圆周均布的12 颗M3 不锈钢螺钉固定在光纤陀螺基座上，其由U 型槽、顶盖和光纤环3 部分组成。光纤环通过胶粘剂粘接在U 型槽内，与其同心，顶盖与U 型槽装配后，激光焊接固定，构成壳体，光纤环组件如图1 所示。

图1 光纤环组件结构示意图Fig.1 Schematic diagram of fiber-optical ring assembly structure

1.2 U 型槽和顶盖的材料参数

光纤环组件中的U 型槽和顶盖采用了软磁合金1J79，其材料弹性模量为200 GPa，泊松比为0.3，密度为8 600 k g/m3；胶粘剂弹性模量为584.62 MPa，泊松比为0.33，密度为1 179 k g/m3。

1.3 光纤环材料组成

光纤环为光纤陀螺提供大面积的闭合回路，其稳定性和抗干扰能力直接影响陀螺的性能[14]，因此本文进行了加速场作用对光纤环形变影响的研究。光纤是构成光纤陀螺光学回路的传感部件，需要根据环路中的顺、逆时针传播光的相位差来敏感转动速率，为提高检测的灵感度，一般光纤的长度为几百米到几千米不等[15]。本文光纤环是由长度为1 km 的光纤按一定的方式缠绕而成，光纤的间隙由胶粘剂填充。绕制完成后的光纤为各向异性复合材料结构，含有石英、光纤内涂层、光纤外涂层和粘胶剂等多种材料。光纤的结构示意图如下图2 所示，所含材料参数如表1 所示。

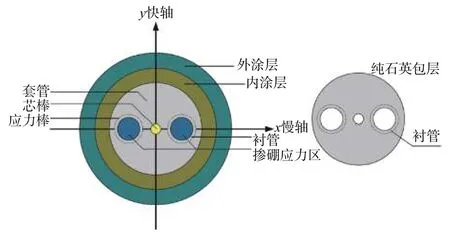
图2 光纤结构示意图Fig.2 Structure diagram of fiber-optic

表1 光纤所含材料参数Table 1 Material parameters contained in fiber-optical

1.4 光纤环等效材料参数

1.4.1 RVE 模型建立

由于光纤环各向异性和均匀化特性，故采用基于RVE（代表性体积单元）分析的细观有限元模型，通过施加周期性边界条件[16]获得RVE 的细观力学响应，以准确获得材料的细观结构与有效模量间的“定量”关系[17]，分析获得光纤环复合材料的基本力学性能参数，以准确模拟光纤环形变。光纤环结构示意图和光纤环横截面视图分别见图3所示。

图3 光纤环结构示意图和横截面视图Fig.3 Schematic diagram and cross-sectional view of fiberoptical ring structure

将光纤环分成多个RVE，因为所有的RVE 都是相似的，所以它们应该表现出相似的应力、应变场，于是可以用一个RVE 中的应力、应变场来反映复合材料体的细观应力及应变场。复合材料承受均匀的远场外载时，由于所有的RVE 都是相似的，那么它们应该表现出相似的应力应变场。因此，从总体上看，应力应变场也应表现出周期性。故可用周期性条件与连续性条件来约束RVE 的边界变形[18]。

一般周期性边界条件的提出是建立在完整RVE 单胞基础上的，RVE 的建立和选取方式是很重要的。由图2 中的光纤结构示意图可知，相对于光纤横截面，芯棒和掺硼应力区的面积占比小，且芯棒和掺硼应力区的主要成分是二氧化硅，因此，为了减少图4 中RVE 单元的节点数，提高计算效率，本文定义芯棒和掺硼应力区的材料为二氧化硅，不在RVE 模型中单独划分芯棒截面。RVE 的选取方式有正方形、菱形、六边形和随机排列。本文选取的RVE 单胞模型为六边形，性能较好，如图4 所示。周期性位移边界条件的施加，都是通过

图4 RVE 示意图Fig.4 RVE schematic diagram

在单胞平行相对面上相应网格节点处建立线性约束方程来实现的，故周期性边界条件也称为“方程边界条件”。周期性边界条件应包括位移连续条件和应力连续条件[19]，这样才能实现不同RVE 间的应力连续和位移连续。

本文采用的周期性边界条件包含刚体位移约束、面上节点约束、棱边节点约束和顶点约束，即施加6 组线性不相关的宏观应力场，分别对6 个节点自由度施加相应的集中力，计算完成后通过有限元后处理，由节点位移求得连续体宏观平均应力值和宏观平均应变值，再运用RVE 的等效本构方程（1），获得复合材料宏观弹性常数[16]。

1.4.2 方法验证

为验证本文所建立模型和程序的准确性，对文献[20]中的算例B/Al 复合材料进行对比验算，对比结果如表2 所示。算例与本文都是对于B/Al 复合材料进行RVE 计算，并对两种方法进行验证，其中算例设定纤维方向为纵向，与纤维方向垂直方向为横向，且该复合材料为横观各向同性材料，而本文根据实际工况设定为各向异性材料，将横向分为两个方向，设为1 和2。表中：Et1为1 向的横向弹性模量；Et2为2 向的横向弹性模量；Ea为纵向弹性模量；Ga1为1 向的面内剪切模量；Ga2为2 向的面内剪切模量；Gt为纵向剪切模量；va为纵向泊松比；vt1为1 向的横向泊松比；vt2为2 向的横向泊松比。

表2 本文与算例的B/Al 复合材料等效弹性性能参数计算结果对比Table 2 Comparison of calculation results of effective elastic performance parameters of B/Al composites in this paper and reference

由对比结果可知，两者计算数据一致性较好，说明本文的建模方法和程序正确可行。

1.4.3 光纤环等效材料参数计算

针对所建立的光纤环RVE 施加周期性边界条件，通过有限元分析获得6 组线性不相关的宏观应力场和变形云图（见图5），图中坐标系方向为：RVE 的x方向为光纤环轴向，y方向为光纤环径向，z方向为光纤环切向。

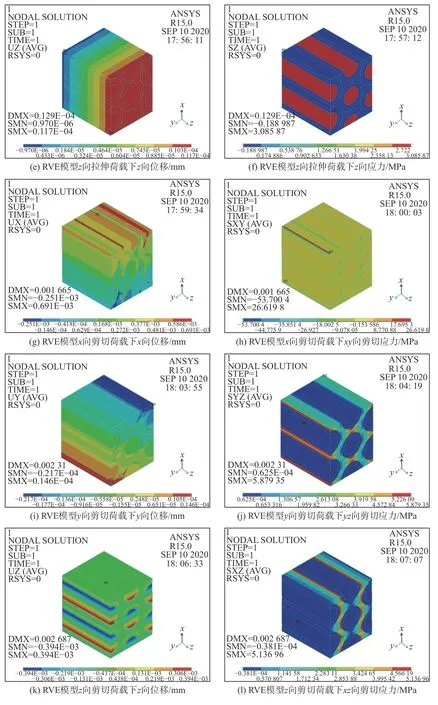
图5 RVE 模型在拉伸与剪切载荷下的应力和位移云图Fig.5 Stress and displacement cloud diagram of RVE model under tensile and shear loads

由图5 中的应力和变形图可以得出：由于光纤环RVE 沿z向材料均匀分布，因此在z方向荷载作用下沿z向的位移场也是均匀变化的，但是由于组成光纤环的各向异性复合材料包括石英、光纤内涂层、光纤外涂层和胶粘剂，它们的材料弹性模量差异显著，因此各材料内结构应力场分布均匀，而各材料间的应力不一致，而且具有超高弹性模量的石英应力最大，说明石英承受的载荷最大；由于光纤环RVE 沿y向材料分布不均匀，因此在y向拉伸载荷作用下，RVE 沿y向的位移场是不均匀的；对比x、y和z向3 种拉伸载荷作用下的x、y和z向位移场可知，前两者的变形相差不大，且都显著高于z向拉伸荷载时的z向变形，这说明RVE 单胞z向的等效弹性模量最大，该结果与实际一致。由3 个方向的剪切载荷计算结果可知：在x向剪切荷载作用下，RVE 的光纤外涂层和胶粘剂所承受的应力较小，沿x向的位移是增加的；在y向剪切荷载作用下，RVE 的光纤外涂层和胶粘剂所承受的应力较大，沿y向的位移是增加的；在z向剪切荷载作用下，RVE 的光纤外涂层和胶粘剂所承受的应力较大，石英部分的位移较大。

通过定义数组，计算出6 种线性不相关的应力场下光纤环RVE 的平均应力、应变。根据1.4.1 节中的RVE 等效本构方程，计算得出RVE细观材料参数，因而光纤环等效材料参数如表3 所示。由于RVE 的坐标系与光纤环组件中的坐标系存在坐标转换的问题，因此表3 定义其中1 方向为光纤环的径向，2 方向为光纤环的轴向，3 方向为光纤环的切向。表中E1、E2、E3分别为正交各向异性RVE 在各方向上弹性模量，G12、G23、G31分别为正交各向异性RVE 单胞模型在各方向上剪切弹性模量，vij为单独在j方向作用正应力σj时i方向的应变与j方向应变比值的负数，即为泊松耦合系数[21]。

表3 光纤环等效材料参数Table 3 Equivalent material parameters of fiber-optical ring

2 光纤环组件有限元分析

2.1 有限元模型建立

利用有限元程序ANSYS 建立光纤环组件的空间有限元模型，采用SHELL 单元模拟壳体（U 型槽和顶盖）、SOLID 单元模拟光纤环和胶粘剂。

2.2 工况和计算模型选择

根据光纤环组件实际工作环境，施加直线加速度场，计算工况包括：1） 工况1，+X向10 g；2） 工况2，+Y向10 g；3） 工况3，−Y向10 g。本文将+X向10 g 加速 度 场 定 义为施加 在 沿+X方向10 g 的重力加速度，其他方向类似定义，其中X方向为光纤环平面方向，Y方向为光纤环轴向，方向如图6（a）所示。

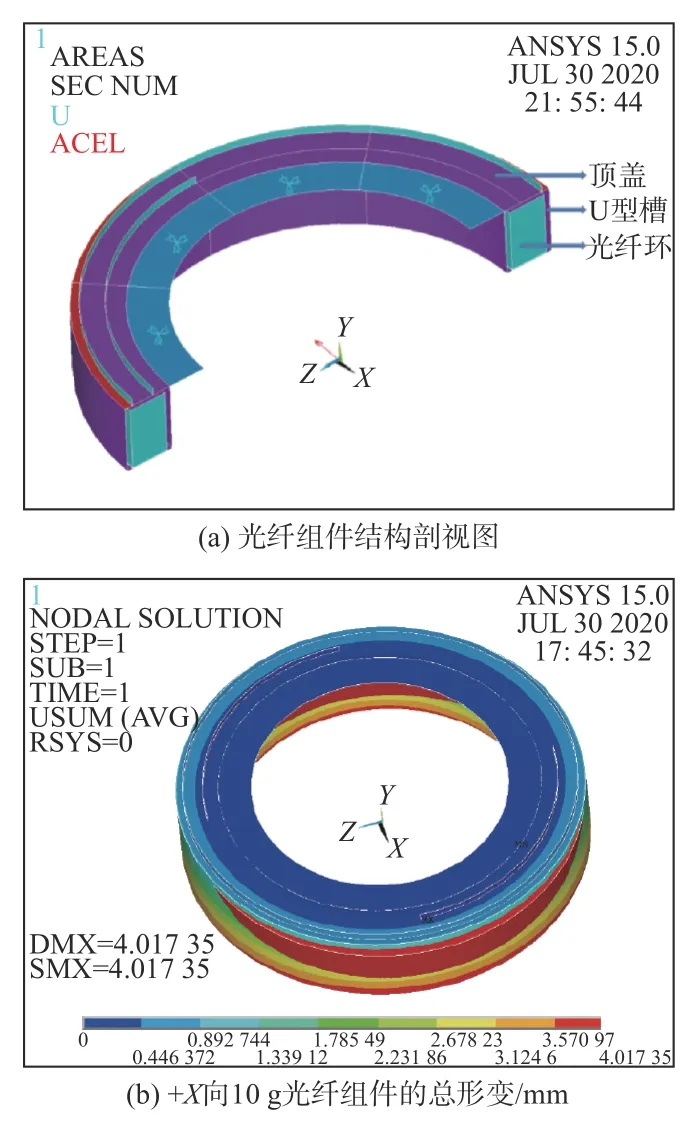
图6 +X 向10 g 光纤环组件的有限元模型和总形变图Fig.6 Finite element model and total deformation diagram of fiber-optical ring assembly structure at 10 g in + X direction

另一方面，根据+X向10 g 加速场作用下的光纤环形变分析结果，如图6（b）所示，光纤环组件的总形变为4.017 mm，已超出光纤环与顶盖、U 型槽间隙，见图6（a），因此，在光纤环的形变过程中可能会受到光纤环与顶盖、U 型槽间的接触挤压影响，即光纤环与壳体的接触影响。故本文需考虑该接触效应，以探讨接触效应与光纤环形变之间的关系。为了便于分析光纤环的形变原因，本文分别选择含壳体与光纤环接触的光纤环组件、不含壳体与光纤环接触的光纤环组件和仅含光纤环本体结构的3 种有限元模型进行对比分析。

2.3 光纤环组件的变形结果分析

工况1：+X向10 g 的有限元计算结果如图7所示。为方便叙述，设定d1为含接触效应的光纤环组件中的光纤环最大变形，d2为不含接触效应的光纤环组件中的光纤环最大变形值，d3则为仅含光纤环本体结构的最大变形值。

当加速场为+X向10 g 时，|d2−d1|=|4.017−2.631|=1.386 mm，说明接触效应可使光纤环形变减小1.386 mm；|d2−d3|=|4.017−0.224|=3.793 mm，说明壳体形变使光纤环形变增加3.793 mm，仅分析光纤环本体结构的变形为d3=0.224 mm。通过分析图7（d）的+X向10 g 接触示意图，光纤环与U 型槽、顶盖产生接触，且光纤环与U 型槽的最大接触压力为10.285 MPa。

因此可知，光纤环与U 型槽、顶盖的接触效应和壳体形变对光纤环的变形产生显著影响，但对于光纤陀螺的高精度测试要求，光纤环本体结构形变d3仍需要考虑。

图7 +X 向10 g 3 种不同接触效应的光纤环总形变和接触压力图Fig.7 Total deformation and contact pressure of optical fiber ring with three contact effects from 10 g in + X direction

图8 +Y 向10 g 和−Y 向10 g 的光纤环总形变Fig.8 Total fiber ring deformation of 10 g in + Y direction and 10 g in − Y direction

如图8 所示，对比工况2 与工况3，即+Y向10 g与−Y向10 g，当−Y向10 g 时，|d2−d1|=|1.684−1.684|=0 mm，说明两者变形一致，当+Y向10 g 时，|d2−d1|=|1.684−1.224|=0.46 mm，因此，当+Y方向施加加速度时，顶盖与光纤环本体结构发生接触挤压现象，该接触效应会影响光纤环的测试结果；而−Y向加

速度时，光纤环所受的力向下，顶盖、U 型槽都不与光纤环本体接触，故接触效应没有影响光纤环的测试结果。

此外，本文还分析了加速度大小变化时光纤环的形变情况，当加速度为6 g 时，加速度载荷减小，U 型槽与光纤环之间仍发生了接触挤压现象，虽然3 种工况中的光纤环组件变形结果减小，但形变规律与加速度为10 g 时一致；当加速度为2 g 时，由于加速度显著减小，且U 型槽与光纤环之间接触挤压较小，因此含接触效应与不含接触效应时的光纤环变形几乎一致。

图9 +X 向10 g、+X 向6 g 和+X 向2 g 含接触效应的光纤环上表面总位移Fig.9 Total displacement of upper surfaces of optical fiber ring with contact effect at 10 g in + X direction, 6 g in+ X direction and 2 g in + X direction

由图9 和图10 光纤环的上表面单元变形云图 可 以 发 现：1） 当+X向10 g、+X向6 g 和+Y向10 g 3 种工况时，由于光纤环与U 型槽、顶盖的接触效应，光纤环产生了较明显的非线性变形，即光纤环与U 型槽、顶盖的接触效应导致结构局部非线性变形，该非线性形变会影响光纤陀螺的失准角测量准确度；2） 当+X向2 g、+Y向6 g 和+Y向2 g 3 种工况时，由于加速度较小，所产生的接触效应影响较小，未发生明显的非线性形变。另外，由图11 可 知，当−Y向2 g、−Y向6 g 和−Y向10 g 3 种工况时，三者情况下的变形不明显，说明光纤环组件受到−Y向的加速度作用，光纤环不与顶盖接触，因此不产生接触效应，光纤环不产生非线性形变。

图10 +Y 向10 g、+Y 向6 g 和+Y 向2 g 含接触效应的光纤环上表面总位移Fig.10 Total displacement of upper surfaces of optical fiber ring with contact effect at 10 g in + Y direction,6 g in + Y direction and 2 g in + Y direction

图11 −Y 向10 g、Y 向6 g 和−Y 向2 g 含接触效应的光纤环上表面总位移Fig.11 Total displacement of upper surfaces of optical fiber ring with contact effect at 10 g in − Y direction, 6 g in Y direction and 2 g in −Y direction

3 结论

本文通过细观力学有限元分析方法获得了光纤环的正交异性材料特性参数，并建立了光纤环组件的空间有限元模型，分析了直线加速度方向和大小影响下的光纤环形变机理，通过以上分析可以得出以下结论：

1） 通过建立光纤环RVE 单胞模型，并施加一般性周期边界条件，计算得出单个RVE 的平均应力、应变，利用本构方程中柔度矩阵与宏观等效应力、应变间的变量关系，可得出光纤环的等效弹性性能参数，实现了各向异性光纤环的有限元模拟，为光纤环组件结构形变分析提供了基础。

2） 根据光纤环组件在不同方向和大小的加速度场作用下的有限元分析，得出光纤环形变影响因素包括3 个方面，即光纤环与U 型槽、顶盖的接触效应，U 型槽、顶盖的形变以及光纤环本体结构产生的形变。例如当加速场为+X向10 g时，接触效应可使光纤环形变减小1.386 mm，壳体形变使光纤环形变增加3.793 mm，光纤环本体结构的变形为0.224 mm，前两者的影响较大，其他工况规律类似。该方法可以为实际工程中减少陀螺光纤环形变和提高光纤陀螺的测量精度提供参考依据。

3） 接触效应使光纤环产生了非线性形变，因此大机动或强振动的高加速度场下，光纤环组件的结构设计应通过结构优化避免光纤环结构件与光纤环的接触挤压，该分析结果为后续光纤环组件的结构优化研究提供了方向。