经历建模过程 感悟模型思想
孙保华

摘 要:模型思想作为一种数学思想,要真正让学生有所感悟需要经历从简单到复杂、从具体到抽象的过程,使学生积累经验,掌握建模方法,逐步形成模型思想。在课堂中,教师需引领学生经历构建数学模型和运用模型解决实际问题的过程,逐步感悟数学模型思想,从而提升学生的思维能力和应用能力。
关键词:小学数学;模型思想;建模;感悟
中图分类号:G623.5 文献标识码:A 文章编号:1009-010X(2021)01-0022-04
数学模型思想就是要让学生经历从具体事物和复杂问题情境中舍弃非本质因素,发现本质要素和数量关系,并加以抽象概括建构数学模型并实现问题解决的过程。要让学生真正感悟模型思想,教师必须要循序渐进地引导学生掌握数学建模的一般方法。只有掌握了数学建模的方法,学生才能初步形成模型思想,感悟模型价值,树立用数学模型解决实际问题的意识。
一、选择素材,让建模有根源
好的素材一方面要和学生的生活实际相结合,另一方面要和学生的实际能力相结合,后者也许更为重要。因为数学模型的建立一定是基于学生对情境的抽象和对问题的表征,然而受限于小学生年龄特征与认知水平,建模前的抽象和表征是基于学生的实际操作,有利于学生经历从发现问题到建立模型再到求解验证的活动过程。因此教师要努力提供与学生日常生活有联系、典型且熟悉的素材,让学生在观察、操作、抽象、概括的过程中形成一般的模式表达。
(一)典型的素材
建立模型思想的本质就是要让学生体会和理解数学与外部世界的联系。为了实现这个目的,教师要为学生提供典型的素材,这样有利于学生更好地观察现实情境,启发思考并提取有用的信息,激发学生探究的欲望,抽象出数学模型。
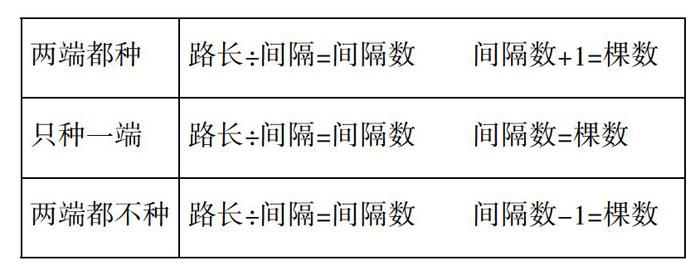
例如,用植树的素材讲解间隔计数问题就比较恰当,因为植树的素材中清晰地蕴含着分割点和间隔,很好地体现了分割点和间隔之间的关系。教学中,可以让学生进行模拟植树,就会发现不同情况下棵数与间隔数之间的关系。这种舍去植树问题的一些非本质属性,形成纯数学的间隔计数问题的关系结构,并用文字语言进行表达(如下图),从而渗透模型思想。
(二)熟悉的素材
弗赖登塔尔认为:数学化的对象就是学生熟悉的现实,而不是成人熟悉的现实。因此,在教学中要尽可能选择学生现实生活中经历过的真实事情和熟悉故事。这些学生熟悉的素材简洁、易懂、容易让其产生亲近感,便于激活已有经验,从而帮助学生建立数学模型。
例如,建立加法运算模型时,教师依次呈现了多个生活实例。
① 同学们在做纸花,小明做了4朵红花,小红做了3朵黄花,两人一共做了多少朵花?
② 草地上有3只白兔,2只黑兔,一共有多少只兔?
这些问题都是学生熟悉的素材,在解决此类问题时,让学生感到不管是求“一共做了多少朵花”,还是求“一共有多少只兔”,其共同点都是将两部分合并起来。教师适时引导学生归纳:把两个数合并成一个数都可以用加法计算。
二、经历过程,让建模有思路
有经历才有感受,只有让学生在思考、探究、交流和求证等数学活动中合理建构数学模型,充分经历从生活原型到数学模型的转变,才能有效培养模型思想。因此在教学中,我们要引导学生通过自主探索、合作交流,经历将实际问题抽象成数学模型的过程。让学生在这一过程中理解、掌握有关知识和技能,积累数学活动经验,感悟模型思想的本质。
(一)抓住建模起点,鼓励提出问题
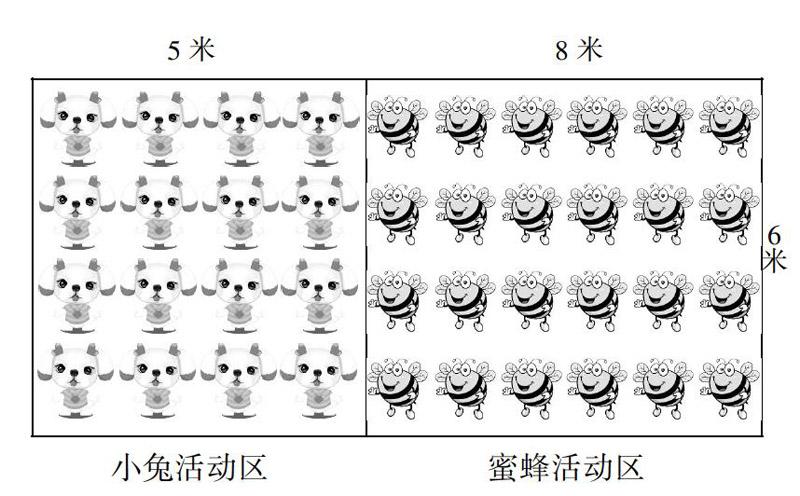
数学模型是以具体问题为载体,学生在建模的过程中要接触多侧面、多层次丰富的现实问题原型。因此,选择的问题要有代表性,要能激发学生建模的兴趣,努力创设利于建模的问题环境,让学生产生学习需要。用数学的眼光观察生活情境并发现和提出问题是数学建模的起点。教师要抓住起点,找准学生认知的最近发展区,引导其提出有价值的研究问题,引发真思考。如“乘法分配律”的教学,出示情境图:
根据小学生的年龄特点和认知水平,课堂上呈现给学生的问题应该是直击知识核心,并能准确反映教学内容的。教师鼓励学生观察情境图,从中获得哪些数学信息,能提出什么数学问题。学生可能从只数出发提问“这里一共有多少只小动物”,也可能从面积出发提问“动物活动区的总面积是多少”。对于这样的典型问题,教师要做到心中有数,只有对典型问题进行深入探究才能让情境成为数学模型的范例。
(二)关注建模抽象,鼓励自主表达
学生提出了有价值的数学问题,教师组织学生在充分感知大量感性材料的基础上,经历观察、比较、操作等活动,引导学生逐步发现这些问题的共性,逐步抽象概括。每个学生的认知水平不同、思维方式各异,因此解决问题的思路也不尽相同,鼓励学生用不同的方式进行表征,从而满足不同层次学生的认知能力和学习需求。
①围绕问题尝试列式,说出思路。要解决“动物活动区的总面积是多少”“这里一共有多少只小动物”这两个问题,要让学生写出思考过程,针对每个问题写出两个算式,并说出想法。
(5+8)×6=5×6+8×6
(4+6)×4=4×4+6×4
每一个问题所列出的两个算式,思路不同,结果相同,可以用等号连接,就形成了一个等式。
②观察等号两边算式,说出发现。等号两边都有加法和乘法,左边是两个数的和乘一个数,右边是两个数分别与这个数相乘,然后再相加。
③多途径多视角验证,增强感悟。提问:像这样的等式是否都有这个规律并进行验证。
计算验证:(70+35)×4 ○ 70×4+35×4
(5+6)×7 ○ 5×7+6×7
舉例验证:一个足球80元,一个排球65元,各买4个,一共需要多少元?
画图验证:
求a b两部分合起来的大长方形的面积也可以说明乘法分配律的合理性,即8×4+3×4=(8+3)×4。
④建立知识间的联系,完善认知。在举例验证的基础上,要让学生思考为什么会有这个规律。其实可以通过运算意义来理解,从而揭示规律的本质。
(5+6)×7 〇 5×7+6×7
11 5个7加6个7
11个7 11个7
⑤运用多种方式表征,丰富模型。情境表征:(上衣的价钱+裤子的价钱)×套数=上衣的价钱×套数+裤子的价钱×套数
文字表征:两个数的和与第三个数相乘,等于这两个数分别与第三个数相乘,再把所得的积加起来。
符号表征:(□+△)×○=□×○+△×○
字母表征:(a+b)×c=a×c+b×c
不同的表征方式表達的是同一个意思,可以在互相借鉴中去寻找既简洁又概括的表达方式。在这样的过程中,学生既有自己的独立思考,又有同学的资源共享,在观察比较中抽象出数学符号的表达式,凸显了用字母表达的优势。
三、灵活应用,让建模有价值
要让学生掌握模型思想,就要让学生运用所建立的数学模型迁移运用到结构相似、具体情境不同的问题解决中,感受模型的应用价值。因此,教师可以在学生经历了建模过程后,引导他们利用这一模型寻找生活中的原型、利用模型解决生活中的实际问题和感悟模型的结构内涵。
(一)根据模型寻找原型
根据数学模型让学生寻找生活的原型,通过举例,讲故事等方法给模型赋予情境。让学生从模型的角度亲近数学、了解数学,有助于他们实现知识的内化,加深对模型的理解,增强其应用数学模型的意识。
例如,“单价×数量=总价”是一个基本模型,学生经历抽象、概括得到这一模型后,可以鼓励其应用该模型寻找生活中的原型。
生1:我去超市买了4支钢笔,每支钢笔6元,一共付了24元。
生2:买了4本练习本,每本3元,一共需要12元。
学生在寻找生活中与“单价×数量=总价”有关的原型并转化为用自己的语言表达出来,沟通了已有经验和新知识的联系,真正实现了思维的转化。
(二)利用模型解决问题
学生用数学模型解决实际问题是对数学模型的再认识,使已经构建的模型不断得到丰富,有助于加深对模型的理解,体验模型的价值。教师可以根据数学模型设计不同的问题,但这些问题一定要源于生活,具有现实意义,这样才可能激发学生解决问题的欲望,让他们看到模型在生活中的广泛应用。
例如,在学生寻找了“单价×数量=总价”的生活原型后,可设计与其相关的实际问题,引导学生将解决该问题的方法和思路进行运用。
问题:学生用的橡皮是2元/块,10元可以买多少块?
①理清问题。首先引导学生理解文字信息,条件有橡皮的单价、购买橡皮的总价,问题要求购买橡皮的数量,显然是有关购物的问题。
②确定数据。购物问题的基本数量关系是总价、数量、单价之间的关系。根据题意,单价和总价都直接提供了,要求的是数量。
③运用模型。根据购物问题模型:单价×数量=总价,但本题要求是数量,所以将此模型变式为:总价÷单价=数量,接着运用这一模型求出橡皮的数量。
④解答问题。10÷2=5(块),从前面的解答过程看,小学数学模型的应用其实并不复杂,按照步骤,一般都能比较容易使问题得以解决。在这里,难点可能是模型系统的确定。
(三)感悟模型结构内涵
对于小学生而言,数学模型建立的过程,本质上就是“数学化”的过程,是学生在数学学习中获得某种带有“模型”意义的数学结构的过程。结合解决实际问题教学,设计“一题多变”练习,有助于学生感悟原型间的联系,体会数量关系(模型结构)的魅力。例如:
河滨小学有块长方形水池,长36米,宽16米。改建后长缩短4米,宽缩短3米,改建后面积减少多少平方米?
河滨小学报告厅原来每排36个座位,有16排,改建后,每排减少4个座位,减少3排,改建后共减少多少个座位?
河滨小学原打算买36个排球,每个16元,实际每个降价4元,且少买了3个,实际比计划少花多少元?
情节虽然不同,但数量关系(数学模型)是相同的。通过这样的变式训练,能让学生感悟到此类问题其实都是来源于同一个模型系统。
四、拓展延伸,让建模有发展
在应用模型的过程中,不能让学生简单套用模型,而应引导学生展示解决问题的思维过程,并对程序的各个部分进行剖析,促进学生分析、解决问题能力的发展与提高。在深入理解模型的基础上,教师可适当地拓展延伸,变换问题情境引导学生通过知识的迁移体会数学模型的一般化思想方法,增加建模的思维厚度,深化模型的内涵。例如:
(1)一条长80米的小路,工人要在路的一边栽树(两端不栽),相邻两棵树之间的距离是5米。一共要栽多少棵树?
(2)学校大门前有一条120米的路,工人要在路的一边栽树。每隔5米栽一棵(一端栽、一端不栽)。一共要栽多少棵?
针对这两种情况,由“两端都栽”的模型“间隔数+1=棵数”,依据前面的基础模型合作探究推导出“两端都不栽”的模型“间隔数-1=棵数”和“只栽一端”的模型“间隔数=棵数”。
(3)李大伯准备在圆形池塘周围栽树。池塘的周长240米,如果每隔20米栽一棵,一共要栽多少棵树?
通过引导学生将只栽一端的线段两个端点重合,理解封闭曲线上植树和只栽一端两种情况的联系。帮助学生直观理解不同情况下植树棵数、分割点和间隔数之间的关系,由此真正理解和建立“植树问题”所有情况的数学模型。学生不仅获得了数学结论,更重要的是在建模的过程中将知识内化、模型内化和思想升华。
总之,模型思想在实际教学中的渗透,不仅有利于学生更好地理解和掌握所学的知识,还有利于学生从数学结构的角度去阐述这些知识的本质。教师在教学实践中要有渗透模型思想的意识,让学生在建立数学模型的过程中,理解数学模型的价值与作用,解释和应用数学模型,增强应用意识。
参考文献:
[1]王永春.小学数学与数学思想方法[M].上海:华东师范大学,出版社,2014.
[2]吴正宪.张 丹.发展学生数学关键能力[M].北京:教育科学出版社,2017.

