一道耐人寻味的二次函数中考题赏析

沈岳夫

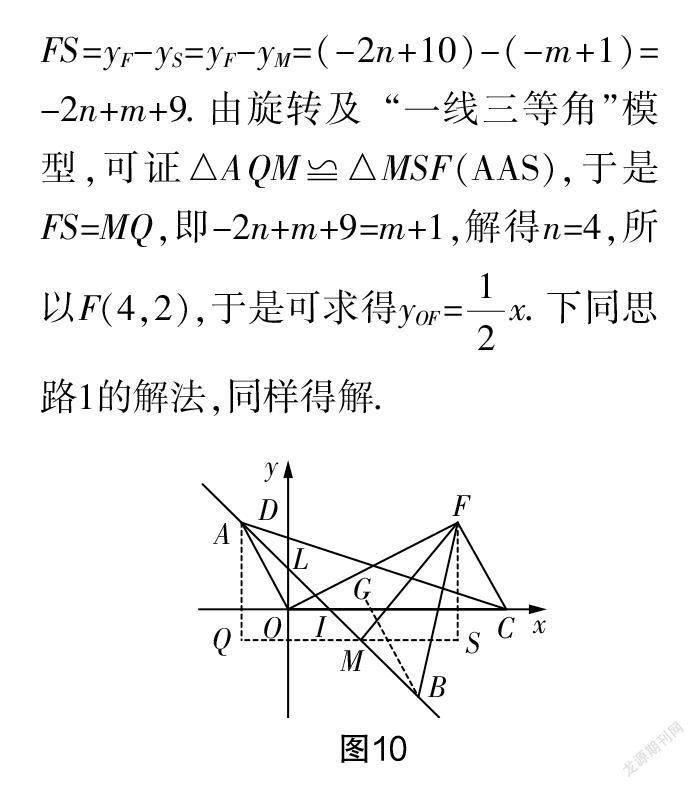
[摘  要] 在研习2020年的各地中考卷时，江苏淮安的一道以二次函数为背景的动态压轴题看似常规，但又不常规，有创意、有难度，思维含量高，成为整卷得高分的“坎”.对于如何化解该题，文章从模型挖掘、一题多解两方面对其第（3）问进行重点剖析，望能对教学有所启迪和帮助.

[关键词] 二次函数;动态问题;解题策略

数学家哈尔莫斯说过，“问题是数学的心脏”. 对问题进行研究是教师的一项基本功，通过研究，挖掘其隐含的问题的本质，获得丰富的教学资源. 这样做，不仅能提高教师自身的专业素养，还有利于开阔学生的思路，培养学生的创新能力. 现以2020年江苏淮安的中考压轴试题为例，着重研究第（3）問的解题思路，不妥之处，请同行指正.

评注 此题解法很多，实际就是面积“斜化直”问题，具有挑战性，有较大难度. 其实第（2）问的设置已搭建起一座精巧的桥梁，有了很好的铺垫.思路1是利用面积的分割，借用“宽高公式”顺势而为;思路2是把已知关系式S1-S2=6进行变形转化，直达本真，化繁难为简捷，充分体现了转化的思想.由此可见，通法、“模型”是数学常规解题的一种有效手段，教学中要让学生理解常见方法，并将该方法领悟透彻，落实到位！

评注 此题含有转化变形的技巧，有一定的灵活性.考生看到此问时，或许会被∠FBA+∠AOD-∠BFC=45°这个条件“吓”得束手无策.究其原因，主要表现在：一是转化意识缺乏，没有把条件等价变形为∠FBA-∠BFC=45°-∠AOD;二是猜想意识贫乏，没有通过画图猜想点F的轨迹（即AF∥x轴）;三是模型意识匮乏，如MA绕点M顺时针旋转90°得线段MF，没有联想到隐藏的“一线三等角”模型.基于此，思路1是通过导角，先有FG∥AO，再判断AF∥OC;思路2先添加平行线，再导角证平行;思路3在证得平行的基础上，构造“一线三等角”. 这三种思路都利用了通过导角证平行的常用方法，试题虽然不难，但对变形能力和推理能力有着较高的要求，因此，这三种不同的变形方式也对提升学生的变形能力及逻辑推理能力大有裨益.

类题迁移

几点思考

1. 提取信息，有效构图

通过对题目的认真阅读，提取有效的关键信息，根据题意构造出分离的几何图形（如图6和图7），灵活运用平时积累的模型，做到“生题寻旧题，联想生思路”，这样解决问题时就如囊中探物，轻而易举.

2. 思路迁移，分类讨论

以二次函数为背景的动态性问题，所涉知识点众多，覆盖面广，条件隐蔽，关系复杂，思路难觅，解法灵活，这就需要考生在充分理解题意的基础上多方位思考、多角度着手、多层次探索（如图8和图9）. 运用类比、归纳、联想、分类讨论以及数形结合、转化等数学思想方法多管齐下，达到化繁为简、化难为易的解题效果.

3. 一题多问，提升思维

解题时设置一系列类题，从形式上看，一问接一问，一环套一环;从内容上看，问问相连，环环紧扣;从目标上看，步步紧逼，层层深入，让问题处于学生思维的“最近发展区”，才能把学生的思维引向一定的高度和深度，进而总结问题的解决策略，高屋建瓴地把握解题方向，提高学生的核心素养.

综上所述，在探索和解决问题的过程中，有序思考，分层推进，凸显了数学解题的三个递进的境界：一是知其然，二是知其所以然，三是如何知其所以然.在日常解题教学中，教师要善于选取、归类、整合典型的试题作为教学素材，注重挖掘题目的通法，提炼解题模型，从而提升学生的思维能力和解题素养.

1196501186315