探究思维障碍成因 引导突破思维障碍

单正凤

[摘  要] 若常常对数学中的错误视而不见、听之任之，久而久之就会形成思维障碍. 若不能突破思维障碍，就会使学生产生畏难心理，不利于健康解题心理的塑造，影响数学思维的发展. 因此，教学中教师应关注错误，分析问题成因，通过启发、训练、疏导等方式帮助学生排除思维障碍，让学生体验成功，树立学习的信心.

[关键词] 思维障碍;畏难心理;突破

在数学学习中，学生常常因思维受阻而中断解题，或是在解题时出错，同时又因思维缺乏多样性和变通性，使得解题陷入了死循环. 久而久之，学生便产生了心理障碍，在遇到新问题时往往情绪烦躁，思路混乱. 是什么造成了学生的思维障碍？教学中应如何进行疏导？笔者选择了几个具有代表性的案例，分析了产生思维障碍的成因，以期和同行交流.

先入为主，影响知识迁移

学生在解题时习惯于使用常用的方法和知识点，对用得较少的知识点或新接触的知识点常感觉不适，从而造成思维障碍.

案例1 有理数及其运算.

师：我们学习了有理数的运算，下面请同学们比较一下分数的大小. （教师PPT展示题目）

-，-，-，-，-

生1：这个很简单，只要通分就可以比较大小了. （很多学生表示赞成）

师：现在给大家几分钟的时间进行计算. （学生积极运算，结果发现分数的分母都是互质的，如果用通分的方法比较，分子会很大，计算起来比较麻烦）

生2：如果用通分的方法计算量很大，那是否可以考虑利用统一分子来进行比较呢？分子的最小公倍数就是60，操作比较简单.

生2的思路提出后，大家豁然开朗，轻松地得出了答案. 在学习中，学生习惯于使用常用方法解题. 比如比较分数的大小时，学生往往先通分，再根据分子的大小来判断分数的大小，而忽视了若分子相同，根据分母的大小也能判断分数的大小，若分子和分母的计算量都很大，则可以通过两两比较的方式，一个一个地突破. 产生这种现象的原因是教学中教师侧重强化训练，忽视了对学生基础知识和基础技能的培养，从而造成学生解决问题的思路过于单一，没有真正认清问题的本质，从而掉入了预设的“陷阱”.

教学反思  要改变这一现状，就要让学生突破先入为主的思维障碍. 首先，学生要养成多观察、多思考的好习惯. 数学题目灵活多变，单一的强化训练只能在短期内提高学生的解题速度，不利于知识的积累和思维的发展. 教学中可以通过一题多解、多解归一等方法，引导学生认清问题的本质，让学生养成善观察、勤思考的好习惯. 其次，注意题目的多样性. 教师在选取练习题时，要注意题目的多样性，善于利用反例让学生经历挫折，从而培养其思维的多样性.

思考角度单一，思维缺乏变通性

学生思考问题时常常从单一知识点或者单一形式出发，缺乏变换，多角度思考问题意识淡薄，从而造成解题思路单一、僵硬、烦琐，思维缺乏变通性.

案例2 七年级兴趣小组实践题.

题目：甲、乙两人步行且同时相向而行，其速度都为1米/秒. 这时丙骑车与甲同时出发，其速度为2米/秒，丙遇到乙后立即返回，遇到甲后又向乙骑行，丙在甲、乙中间往返，直到甲、乙相遇. 若甲、乙两人步行的距离为100米，请问丙共骑行了多少米？

师：请同学们分组讨论，分享一下你们的解题思路.

生1：我们组认为可以分段考虑，首先计算丙与甲同时出发遇到乙时骑行的距离，然后计算从乙到甲的距离，分段计算后再相加.

师：你能知道分为几段吗？

生1：这个算起来好像有点复杂，要一段一段地慢慢计算，可能需要一些时间.

师：是否还有其他的思路呢？比如是否可以求出甲、乙相遇共需多长时间？（教师发现学生纠结于分段数的计算，及时进行引导）

生2：哦！根据路程和甲、乙的速度，可以求出他俩在步行50秒時相遇，丙的骑行时间也为50秒，再根据丙的速度为2米/秒，可以得出丙骑行的距离为100米.

该案例中，学生刚开始分段进行考虑，但解题时碰壁，教师便引导学生从整体出发，换个思路求解，于是解题变得易如反掌. 在数学学习中，学生常常陷入一种解题思路而无法自拔，其主要原因是缺乏多角度思考问题的能力. 解题时学生习惯于模仿和套用固定方法，其思维缺乏变通性，当思维受阻后便束手无策.

教学反思  在数学学习中，如果思维缺乏变通性，成绩就很难得到提高. 因此，教师在平时不妨通过改变问题、改变已知、改变结论等变式训练，让学生经历题目的“变”，从而引发思维的“变”，进而培养学生多角度思考问题的好习惯. 这样既有利于学生突破思维障碍，又能培养学生的自主探究能力.

分类讨论意识薄弱，思维缺乏严谨性

分类讨论思想是初中生必须掌握的一种数学思想，合理分类可以让复杂的问题简单化、模糊的问题清晰化. 若不能准确地把握分类标准而盲目进行分类，往往会使求解方式产生偏差或错误. 教学中教师必须引导学生确定分类标准，知晓何时分类，善于利用数形结合解决问题，从而使学生的思维更加严谨和缜密.

案例3 代指不明.

（为检测学生的数学思维能力，教师采用了问卷调查的方式. ）

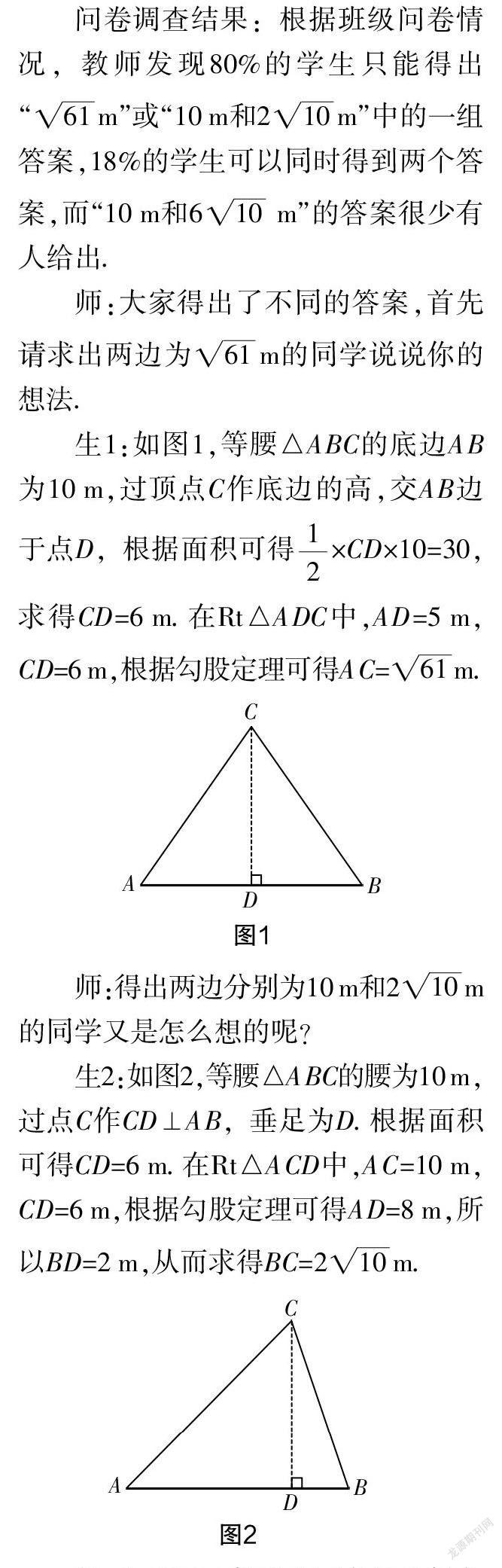
某小区欲铺设一个等腰三角形草坪，草坪的面积为30 m2，已知一条边的长度为10 m，请问另两条边的长度分别为多少？

问卷调查结果：根据班级问卷情况，教师发现80%的学生只能得出“m”或“10 m和2m”中的一组答案，18%的学生可以同时得到两个答案，而“10 m和6 m”的答案很少有人给出.

师：大家得出了不同的答案，首先请求出两边为m的同学说说你的想法.

生1：如图1，等腰△ABC的底边AB为10 m，过顶点C作底边的高，交AB边于点D，根据面积可得×CD×10=30，求得CD=6 m. 在Rt△ADC中，AD=5 m，CD=6 m，根据勾股定理可得AC=m.

师：得出两边分别为10 m和2m的同学又是怎么想的呢？

生2：如图2，等腰△ABC的腰为10 m，过点C作CD⊥AB，垂足为D. 根据面积可得CD=6 m. 在Rt△ACD中，AC=10 m，CD=6 m，根据勾股定理可得AD=8 m，所以BD=2 m，从而求得BC=2m.

师：生1和生2都认为三角形为锐角三角形，难道就没有其他的可能性了吗？

从问卷调查的结果和解题过程来看，学生的分类意识不强，分类也不准确. 首先大部分学生给已知边强加了条件，认为已知边是底边或者是腰;其次学生又对三角形的形状做了限定. 造成这一现象的原因可能是学生缺乏日常的分类训练，以致分类意识淡薄，忽视了分类讨论的重要性.

教学反思  分类讨论思想的应用十分广泛，比如当出现图形位置不确定、图形形状不确定、边角指代不明等情况时都需要进行分类讨论. 教师在教学中要有意识地对学生进行训练和引导，让学生掌握分类的方法，知晓为什么分类、何时分类，克服分类的盲目性和主观性，从而培养学生思维的严谨性和全面性.

消除畏难情绪，树立学习信心

部分学生的学习意志薄弱，遇到外界环境干扰时就很难静心思考，从而使情绪受到影响. 当产生情绪障碍后，学生思维受阻，认知混乱，面对题目无從下手，从而产生畏难情绪，导致学习效率低下. 长此以往，当遇到陌生题目时学生就会紧张，以致心理失衡，进而导致思维失衡，无法正确解答问题.

案例4 已知a，b为实数，ab≠1，且2a2+1234567890a+3=0，3b2+1234567890b+2=0，求的值.

题目解析：由于题目给出了庞大的数字作为干扰项，学生看到后心情烦躁，感觉无从下手，于是便产生了严重的畏难情绪. 在畏难情绪的影响下，学生思维混乱，失去了基本的分析能力. 如果定心分析，不难发现a是方程2x2+1234567890x+3=0的一个根;b是方程3x2+1234567890x+2=0的一个根，即为方程2x2+1234567890x+3=0的一个根. 又因为a≠，所以=a·=.

教学反思  学生在遇到庞大的数字或者不熟悉、不擅长的内容时，常常不知所措，不断给予自己心理暗示，认为这个题目很难求解，从产生厌烦的情绪. 教学中教师必须重视这种现象，及时疏导学生的情绪，让学生多体验成功，加强学生克服困难的决心和勇气，逐渐培养学生的自信心.

总之，学生做题时产生的思维障碍是日积月累形成的，若想消除思维障碍，就必须建立长期的目标. 在教学中，教师应善于观察和分析学生的心理变化，启发学生从多角度思考问题和解决问题，进而突破思维障碍，使思维得到锻炼和健康地发展.

1820501186380