数学问题解答
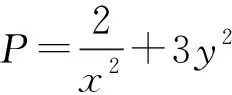
(安徽省六安第二中学 陶兴红 237005 )
解由y3(5-2x3)=3,可得
所以由均值不等式得
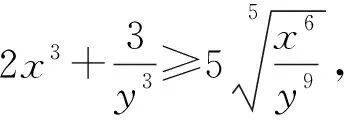
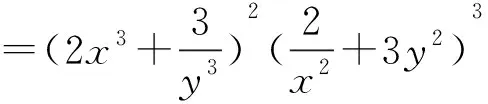
即52P3≥55,所以P≥5,
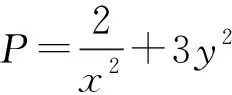
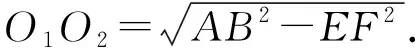
(河南辉县一中 贺基军 453600)
证明设四边形AEFB的周长为p1,△CEF的周长为p2,由题设知p1=p2,过点B作直线BG∥AD,延长CA交直线BG于点G,如图.
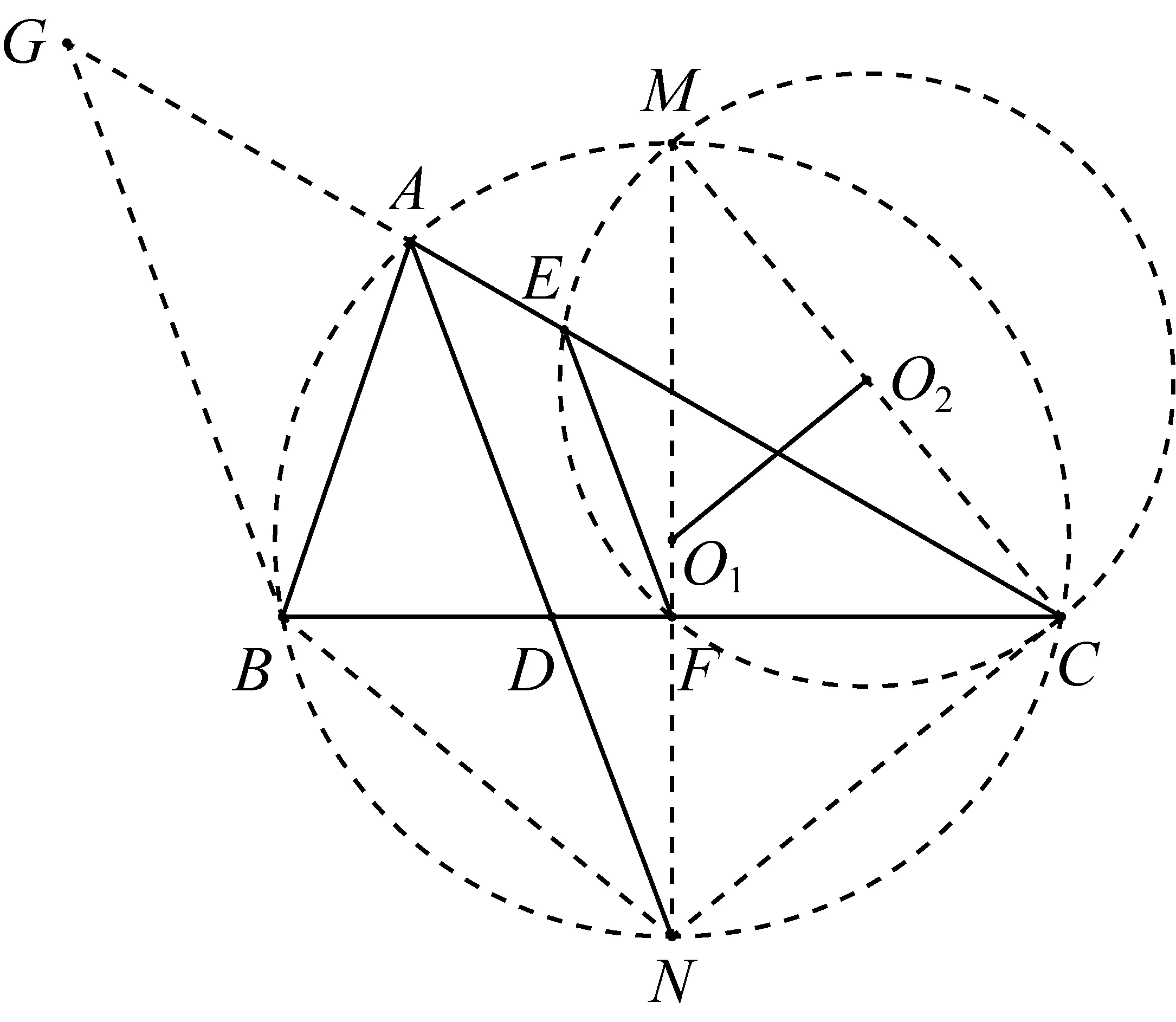
因∠AGB=∠CAD=∠BAD=∠ABG,
故AG=AB,EG=EA+AB.
在△CGB中,EF∥AD∥GB,
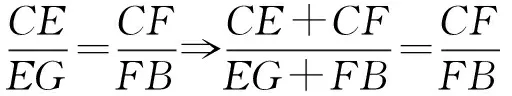
由p1=p2得CF=FB.
根据题设,△ABC的外接圆记作圆O1,△CEF的外接圆记作圆O2. 延长AD交圆O1于点N,连接并延长NF交圆O1于点M,连接BN,CN和MC.
在圆O1中,由∠BAN=∠CAN知BN=CN,又由BF=CF知直线FN垂直且平分BC,因此MN是圆O1的直径,MN的中点是O1.
由∠CEF=∠CAN=∠CMF知M,E,F,C四点共圆即M在圆O2上,因此圆O1与圆O2除交点C外另有交点M.
在圆O2中,∠MFC=90°,因此MC是圆O2的直径,MC的中点是O2.
在△ABC和△CEF中,由正弦定理得
由∠ACB=∠ECF=30°得
O1M=AB,O2M=EF.
在△O1O2M中,可得∠O1O2M=90°,
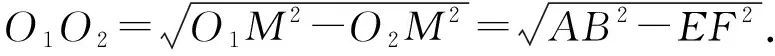
2578已知正实数x,y,z满足x+y+z=1,求证:
(浙江省海盐县元济高级中学 张艳宗 314300;北京航空航天大学图书馆 宋庆 100191)
证明首先证明如下不等式.
当x,y,z>0时,
9(x+y)(y+z)(z+x)
≥8(x+y+z)(xy+yz+zx).
由于
9(x+y)(y+z)(z+x)-8(x+y+z)(xy+yz+zx)
=(x+y)(y+z)(z+x)-8xyz
=x(y-z)2+y(z-x)2+z(x-y)2≥0
上式即证.
由柯西不等式,
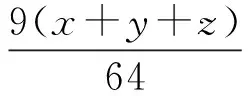
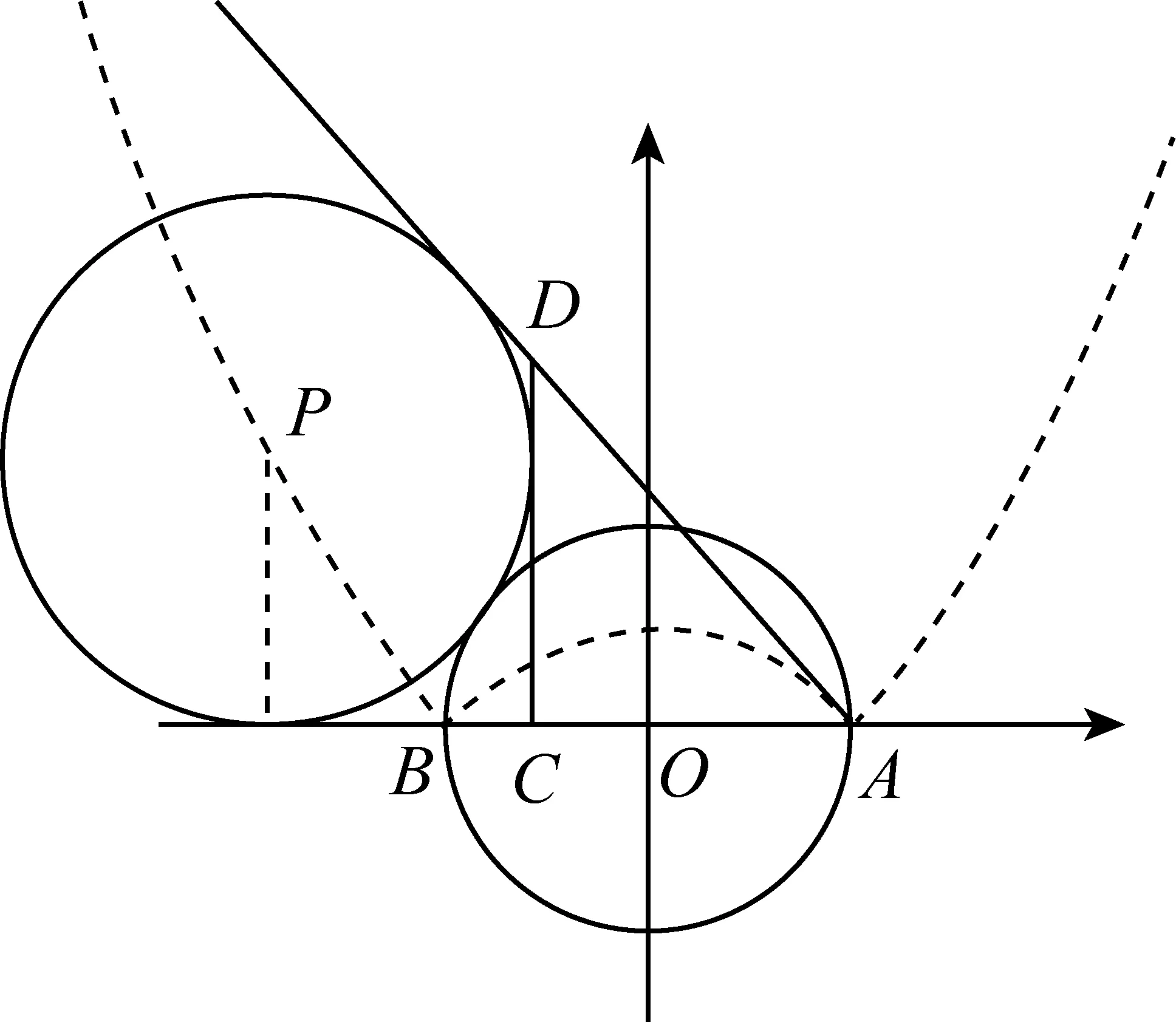
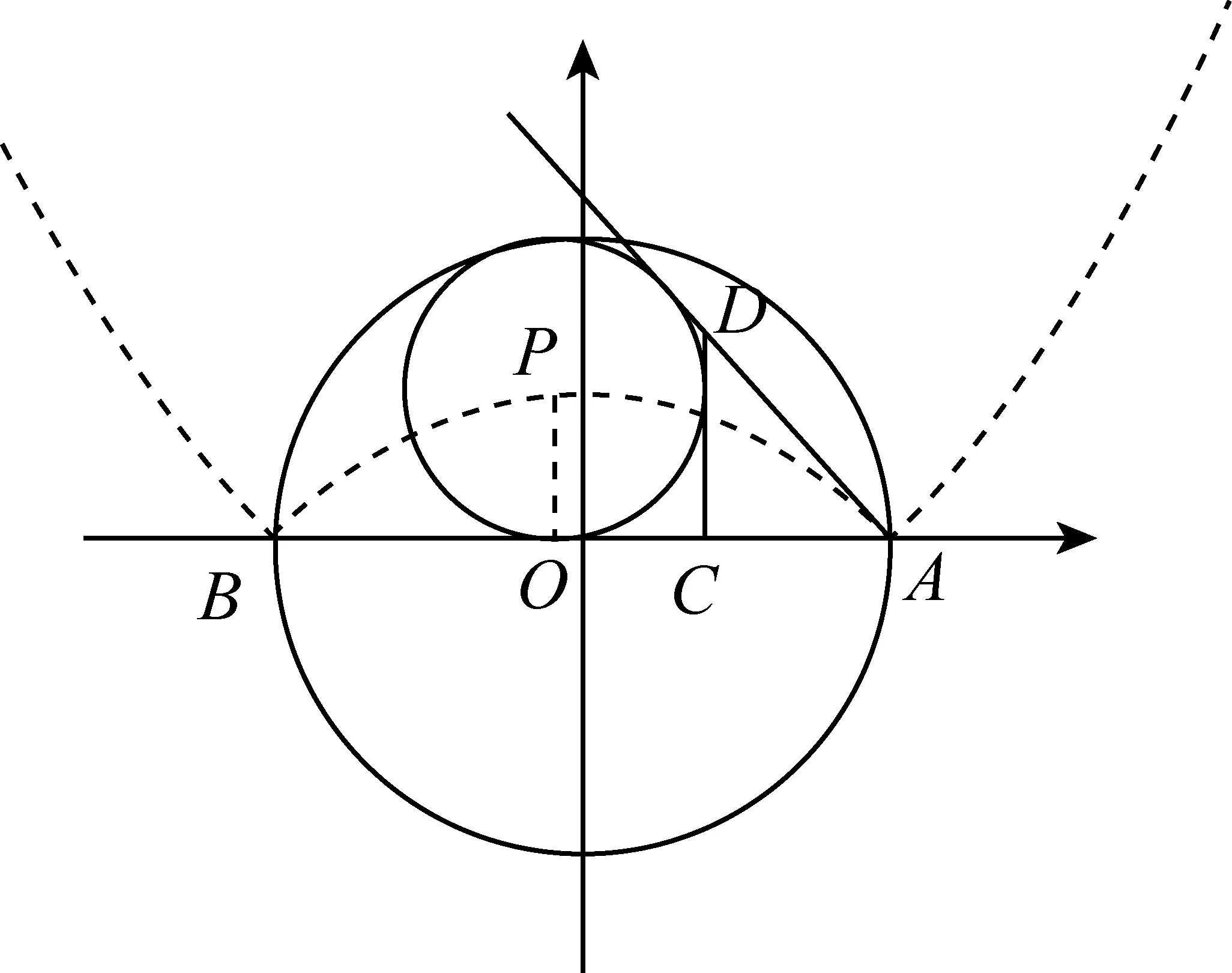
2579以AB为直径的圆⊙O的方程为x2+y2=1,A(1,0).C为射线AB上一个动点,D位于直线AB上方,DC⊥AB于C点,△ACD的CD边的旁切圆⊙P与⊙O相切.试证:P点的轨迹方程为2y=|x2-1|,(x<1且x≠-1).
(浙江台州市洪家高级中学 邬天泉 318000)
证明以BA为x轴,BA的垂直平分线为y轴建立直角坐标系,A(1,0),设C(a,0).以AB为直径的圆的方程为x2+y2=1,
(1)
设△ACD的CD边的旁切圆的方程为
(x-a+b)2+(y-b)2=b2,
(2)
这里P(a-b,b),(b>0).
联立(1)(2)得两圆的根轴方程为
2(a-b)x+2by=(a-b)2+1,
(3)
由于上述两圆相切,
则原点O到直线(3)的距离为1,
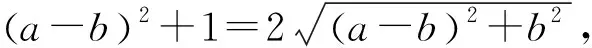
即 |(a-b)2-1|=2b,
(4)
即动点P的轨迹方程为
2y=|x2-1|.(x<1且x≠-1)
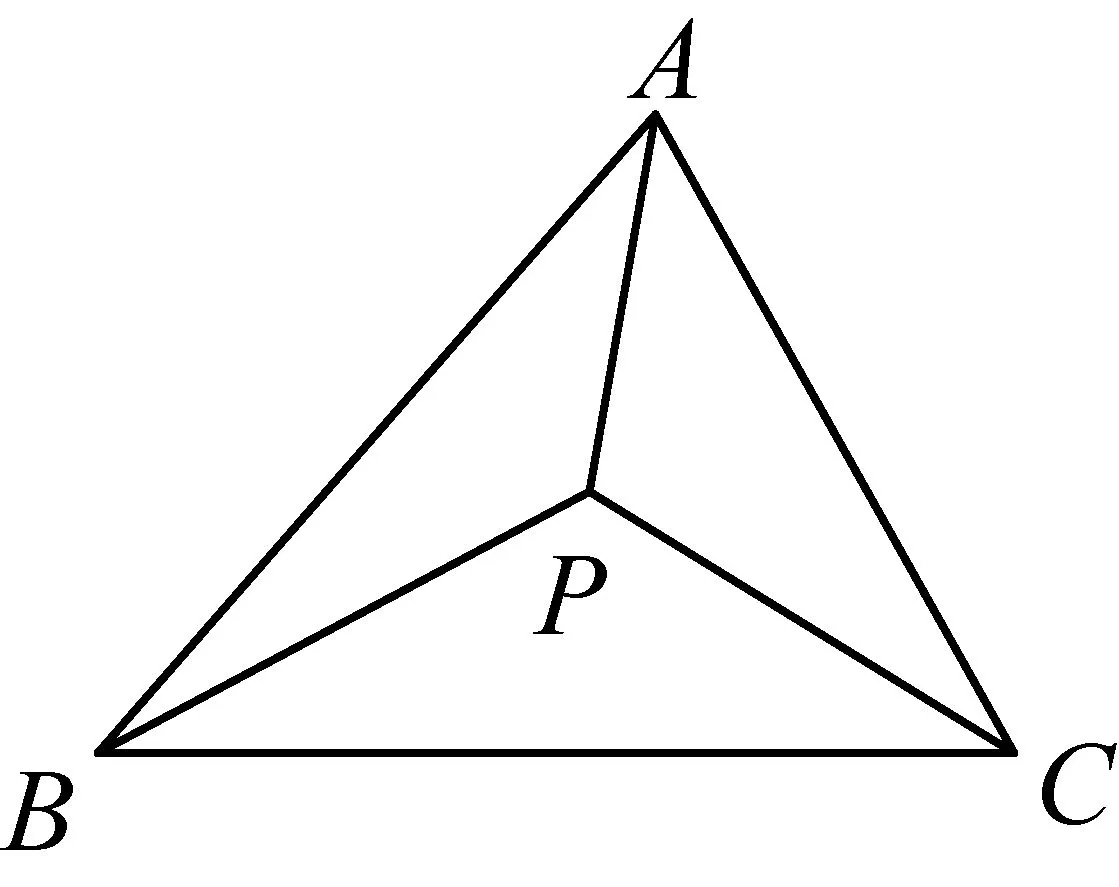
2580如图所示,在△ABC中,三内角A,B,C的对边分别为a,b,c,P为△ABC内一点,且∠PAB=∠PBC=∠PCA(即P为△ABC的勃罗卡点),△ABC的外接圆半径为R,△PBC,△PCA,△PAB的外接圆半径分别为R1,R2,R3,则
(1)R1R2R3=R3;
第三,后期维护由所有权人负责。较大规模的工程,一般是建立工程管理机构,由其负责供水管理以及包括管道工程在内的工程维护;小规模的供水工程,一般由受益村自用自管。
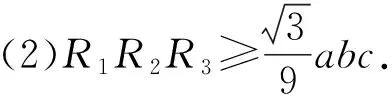
(河南质量工程职业学院 李永利 467001)
证明设∠PAB=∠PBC=∠PCA=α,
则在△PBC中有
∠BPC=π-α-(C-α)=π-C,
由正弦定理可知
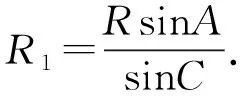
以上三式相乘即得(1)式.
由(1)式和恒等式abc=4Rrp可知,
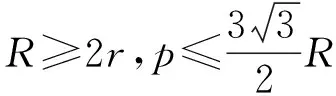
故(2)式成立.
2021年1月号问题
(来稿请注明出处——编者)
2581如图1,半径为r、R的⊙B、⊙C外切于点A(R>r),两圆的一条外公切线与⊙B相切于点D,与⊙C相切于点E,点H1、H2在BC上,且BH1=CH2.过点A作DE的垂线,与过点H1垂直于BC的直线相交于点F1,与过点H2垂直于BC的直线相交于点F2.
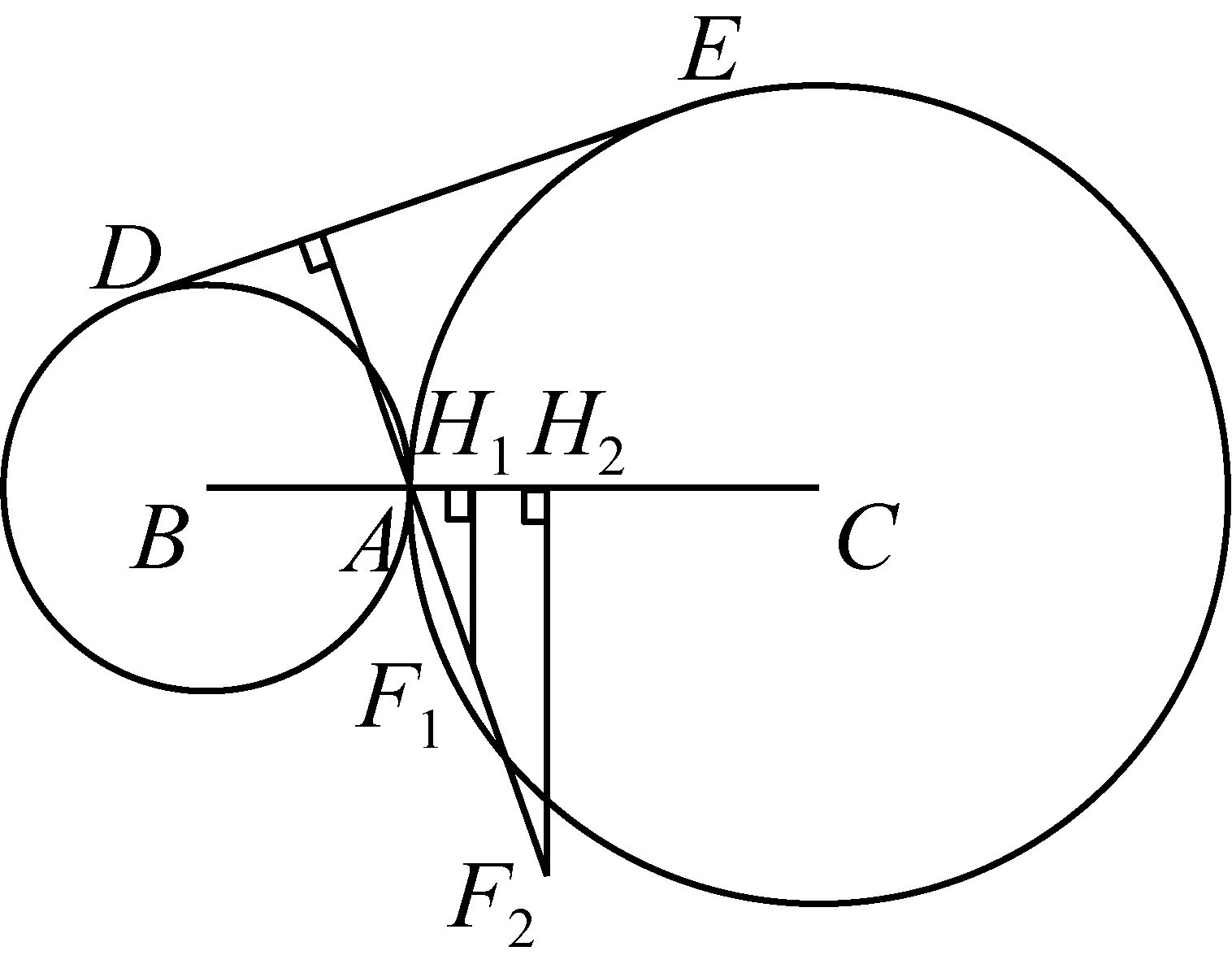
图1
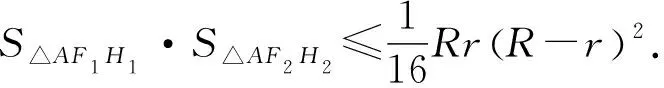
(北京市朝阳区教育研究中心 蒋晓东 100028;北京市朝阳区芳草地国际学校富力分校 郭文征 100121)
2582设a,b,c,d>0,a+b+c+d=4.求证:
abcd(a2+b2+c2+d2)≤4.
(陕西省咸阳师范学院教育科学学院 安振平 712000)
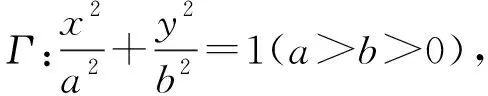
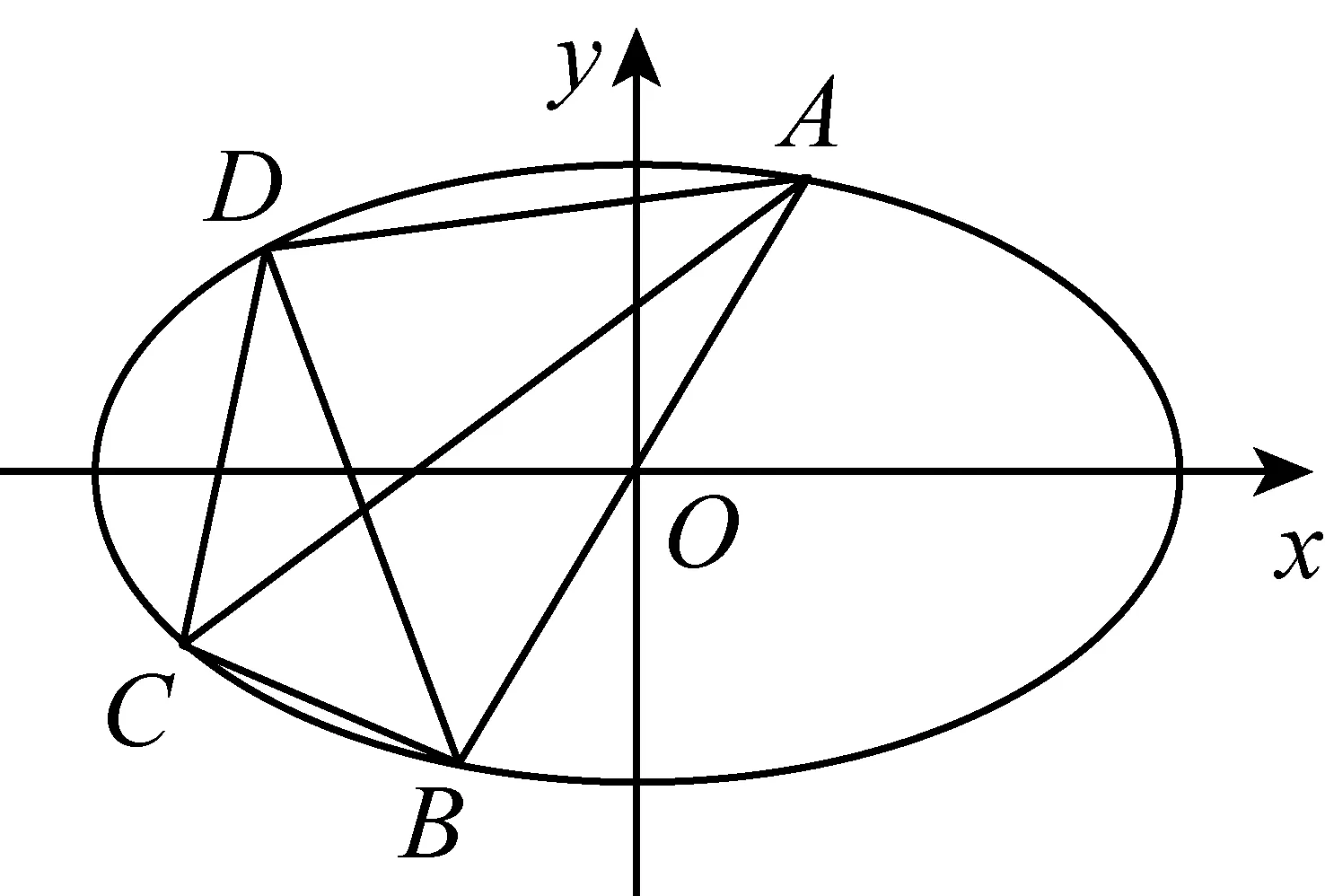
(江苏省徐州市第一中学 张培强 221140)
2584在△ABC中,三内角A、B、C所对边长分别为a,b,c,外接圆、内切圆半径和半周长分别为R、r和s.试证:
(浙江湖州市双林中学 李建潮 313012)
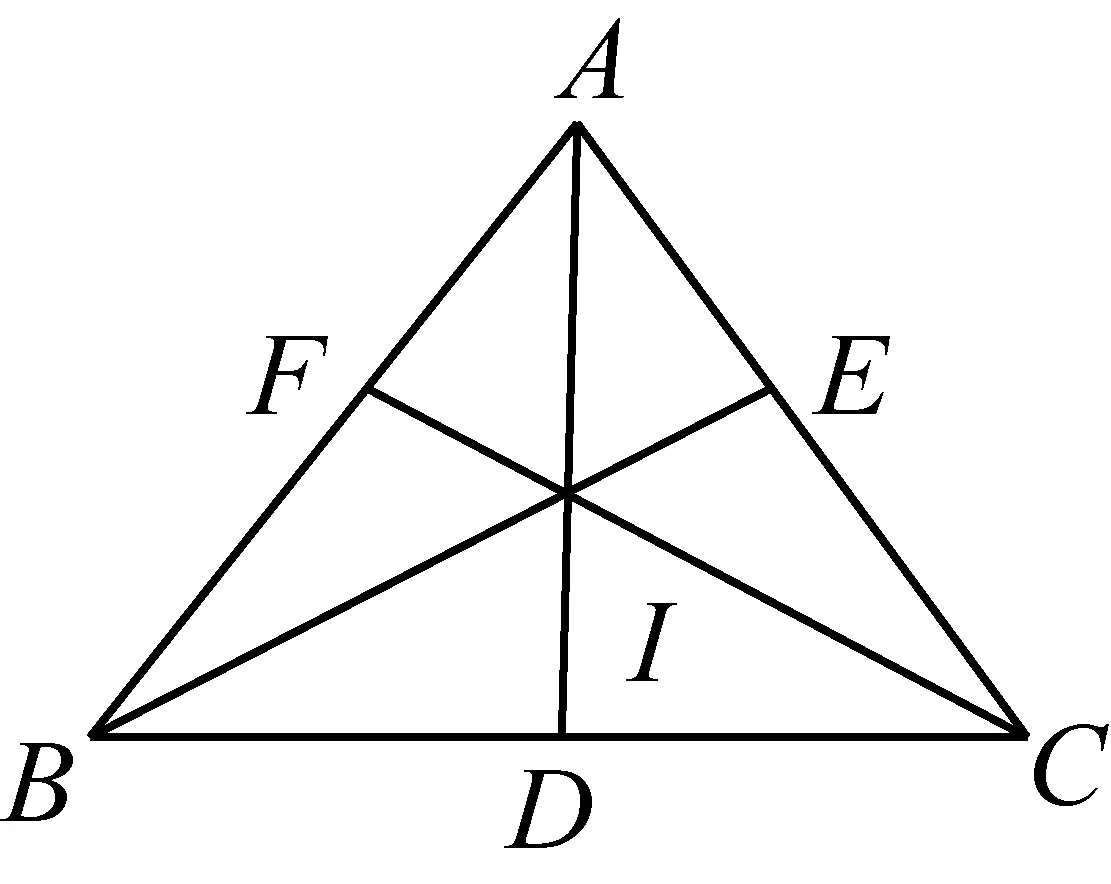
2585如图,点I为△ABC的内心,直线AI,BI,CI分别交线段BC,CA,AB于点D,E,F,记S△BID=s1,S△CID=s2,S△CIE=s3,S△AIE=s4,S△AIF=s5,S△BIF=s6,求证:
(山东省泰安市宁阳第一中学 刘才华 271400)

