顺应学生思维 寻找突破路径①

张文海

(江苏省苏州实验中学 215011)

1 问题背景

《普通高中数学课程标准(2017年版)》指出：“数学教学既要关心学生学习的结果，更要重视学生学习的过程.在学习的过程中掌握数学方法，解决实际问题，促进数学思维发展，形成规范化思考问题的品质，养成不惧困难、严谨求实的科学精神.”因此，在数学教学中，教师应掌握学生的最近发展区，顺应学生思维的发展，找准思维的障碍节点，带领学生一起攻克困难，亲历难点突破的过程，才能让学生提高学习数学的信心，真正掌握解决数学问题的方法.

近期我校高三年级进行了一次数学测验，其中一道解析几何题的答题情况让人大吃一惊.本题第(1)问4分，第(2)①问6分；②问6分，最终笔者所任教理化班的班级均分只有10.59，全班44人只有6人将(2)②问完全解答正确，8人得到△PQG面积的表达式后无疾而终.究其原因，其与解析几何教学中的一些弊端有关.

目前，解析几何的教学存在重思路分析、轻运算示范的现象，导致学生想想都会，一算就错的情况.针对解析几何中运算繁琐的直接思路，笔者认为不宜简单越过，选择其他的解决方法，而有必要沿着学生的思路，站在学生的角度实施教学计划，帮助学生将解题的“最后一公里”打通，这对学生关键能力及必备品格的培养是重要的.

2 题目再现

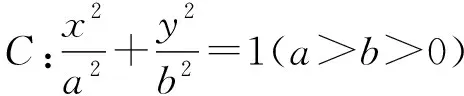
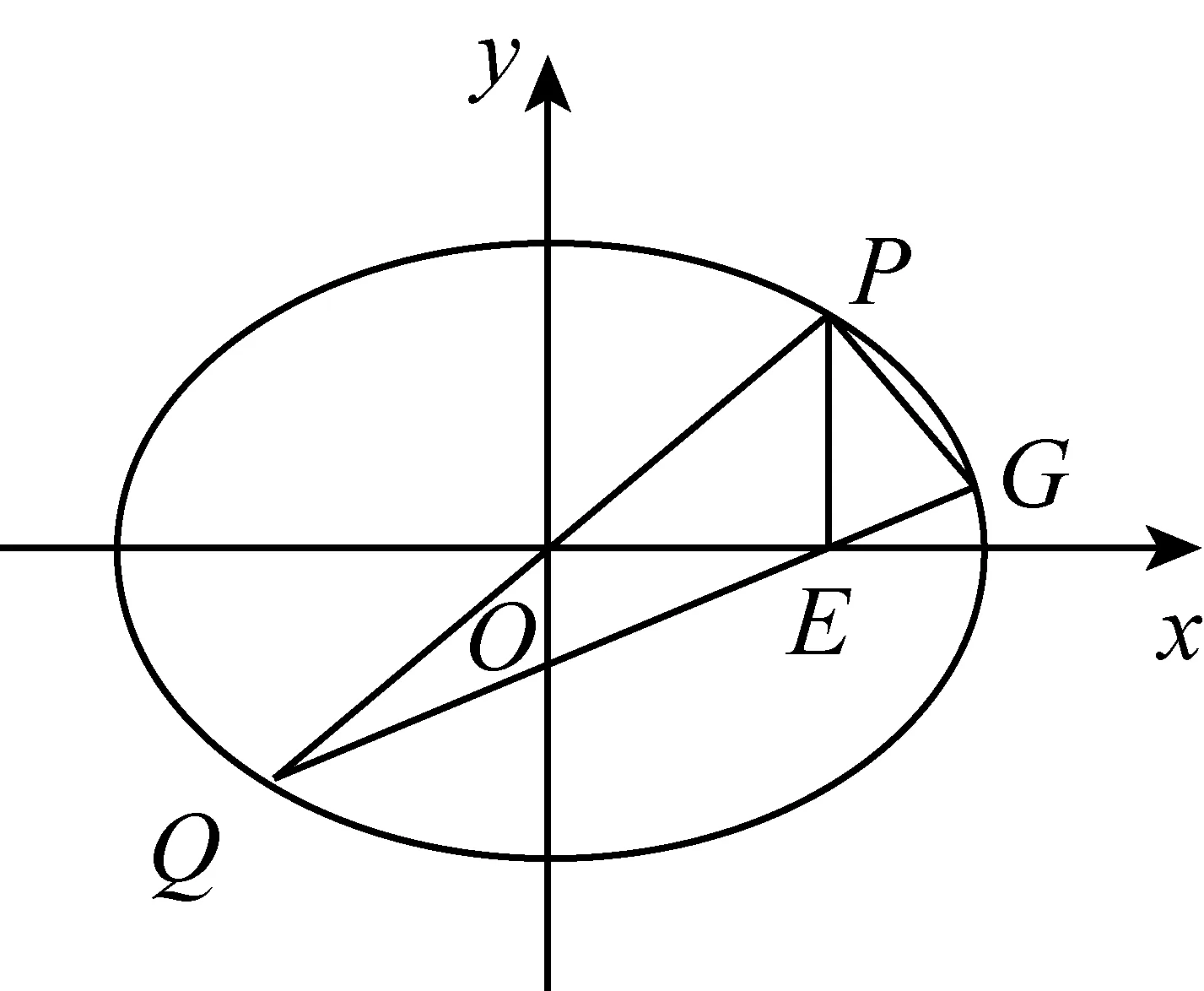
(1)求椭圆C的标准方程；

(2)过坐标原点的直线交C于P，Q两点，点P在第一象限，PE⊥x轴，垂足为E，连QE并延长交C于点G.

①求证：△PQG是直角三角形；②求△PQG面积的最大值.

3 展学生之惑，寻突破之道

从学生的答题情况来看，主要存在两个问题：一是对图形结构特征认识不清，没有能够表示出面积的表达式；二是建立了面积的数学模型，但对式子的本质认识不到位，没能找到恰当的解模方法.今天这节课，我们一起来探讨如何突破这两个难点．

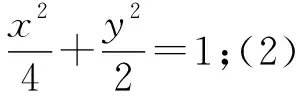
3.1 教学片段1：观察图形，合理选择面积表征路径

《普通高中数学课程标准(2017年版)》明确指出：数学运算是在明晰运算对象的基础上，依据运算解决数学问题的素养．由此可见，运算的基础基于运算对象，表示运算对象的路径选择不同，运算方法的选择也不同，导致运算的长度和繁简程度也不尽相同．因此，在直观感知图形建立运算模型时，结合自己已掌握的基本知识、基本方法以及基本活动经验，从大脑中选择相应的元认知对图形信息进行最近的表征，在观察比较分析中，合理选择面积的表征路径．

师：要解决第②问的问题，我们首先要把△PQG的面积表示出来，大家有哪些想法？

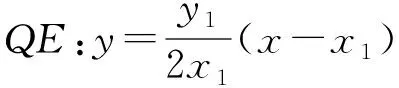
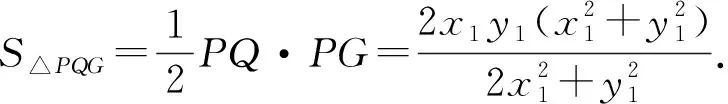
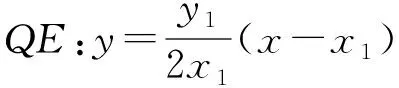
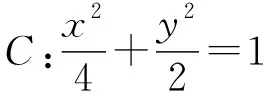
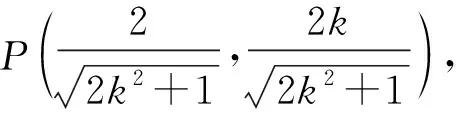
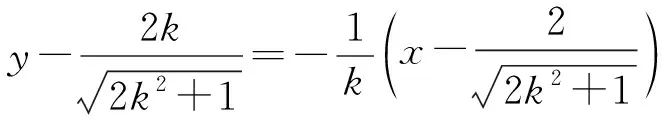
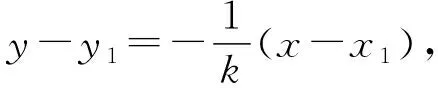
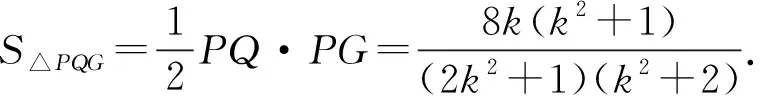
生5：我发现点O是线段PQ的中点，PE⊥x轴，由此我们可以换一种方式来建立面积模型，

S△PQG=S△PQE+S△PGE=2S△POE+S△PGE

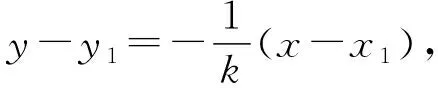
大部分同学发现点P是一个“主”动点，只要它的位置确定，其余点的位置随之而定，故采用了路径(1)、(2)设点坐标的方法来建立面积函数.路径(1)是直线和椭圆联立解二元二次方程组，路径(2)是两条直线联立解二元一次方程组.从运算的繁琐程度来看，可以发现解二元一次方程组比解二元二次方程组要简单，所以路径(2)要更优化.路径(3)、(4)是先设直线PQ的斜率写出方程，求出点P、G的坐标，再表示面积.问题在于点G的坐标不易表示，导致解题失败.路径(5)利用图形的几何特征，将三角形进行分割表示，解题过程相对简洁.

对于多个动点变化的问题，以“主”动点为研究对象是常规思路之一，它的优势在于表示其他点的坐标较为方便，劣势在于目标中至少会含有两个变量以上，消参对学生来讲是一个棘手的问题.设斜率作为变量表示目标，也是处理解析几何问题的常规思路之一.它的优势在于变量少，学生心理感受好，易于接受，敢于下笔，劣势在于表示点的坐标略显繁琐，导致运算量增大，也是导致运算无法进行到底的主要障碍.故在选择解题路径之前，应结合题目的具体条件，确定大致的解题方向，预估解题的运算量，合理选择设“点”法或设“斜”法.此外，解析几何研究的对象是几何图形，既强调用代数的方法刻画几何图形，也强调用几何特征来引导代数的运算和证明.这就是“先用几何眼光观察，再用坐标法解决”，也是解决解析几何问题的一种基本思想．

3.2 教学片段2：分析算式，恰当预判运算过程方法

解决数学问题的过程实质上是从未知到已知的转化过程．要实现这种转化，必须坚持科学的观察方法和理性的思维方式．对同一数学材料进行观察，如所选择的观察角度不同，往往会产生不同的处理方式．我们要用数学的思维方式去分析题目条件和目标数式的结构特征，激活原有的知识和经验,恰当预判运算过程方法，不仅能培养学生良好的观察能力、分析能力和知识的综合运用能力,同时每一个问题的解决过程都是一次知识的重组和整合,对建构良好的认知结构有促进作用.

路径1直面问题，消元求导，夯实运算硬功夫

生众：第1个，变量只有一个，可以求导处理.

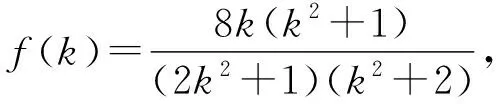
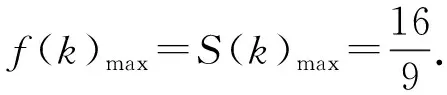
导数法是研究单变量函数最值问题的常用方法之一，它对求导公式的掌握及因式分解的能力要求较高，需要我们具备扎实的基本功和运算能力.

师：如果当初建模时，选择的是设点法，得到目标函数中就含有两个变量，那么又该如何处理呢？处理双变量或多变量函数的基本方法是什么？

生6：利用消元法将双变量减为单变量，再用导数法求解.

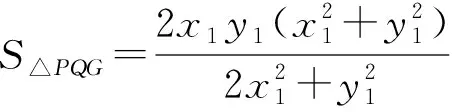
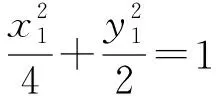
师：你说说，怎么消元？

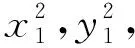
师：生6的问题，谁能帮忙解决的？

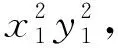
师：大家思考一下生7的想法可行吗？

生众：行.可是次数有点高，恐怕有点繁.

师：我们来试试，既然理论上行得通，我们来实际操作一下，看到底行不行得通.

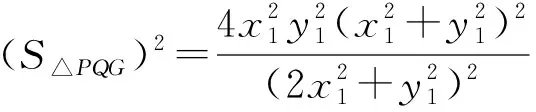
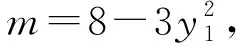
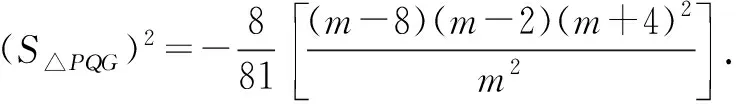
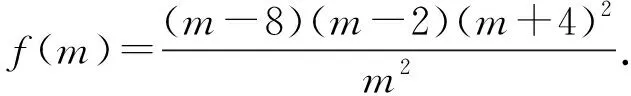
师：接下来，是作为分式函数求导，还是将分子展开，转化为一个多项式函数求导方便？

生8：因为分子是三个因式之积，而分母很简单，所以我认为后者方便一些.

师：分析得有道理！

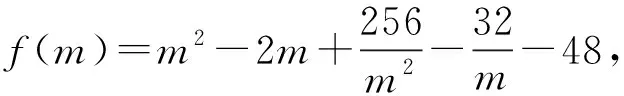
令f′(m)=0，因为m∈(2,8)，所以解得m=4，当20，故y=f(m)单调递增，从而当m=4时，f(m)min=-32，

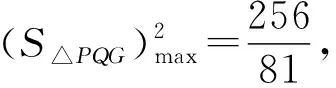
路径2观察结构，构造齐次，激活直觉新思维

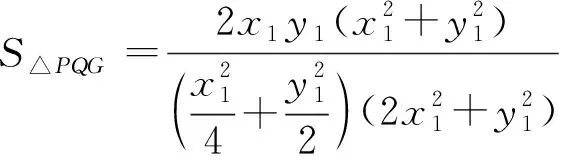
对于二元齐次分式，我们常见的处理方法是什么？

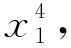
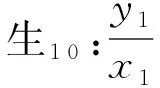
路径3引参变换，三角换元，妙用转化巧突破

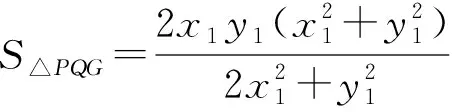
生众：三角换元.

师：运用三角换元的好处在于可以让变量之间的内隐关系外显，有利于根据式子的结构，寻求到合适的处理方法.

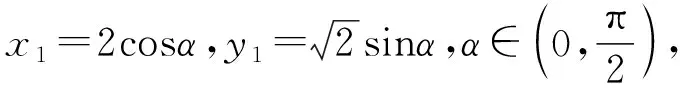
师：大家观察一下这个式子的结构，结合三角函数的知识，你会如何处理？

生11：因为这是一个分式，所以我想到“弦化切”，但它又不是齐次式，需要在分母上添加“sin2α+cos2α=1”构造齐次分式，将面积转化为关于“tanα”的单变量函数.

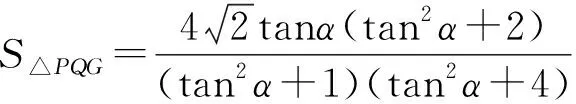
对于上式，我们还可以有如下两种处理方案：

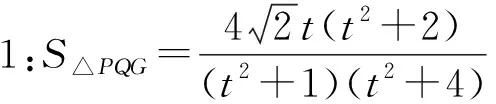
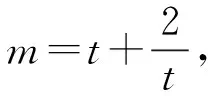
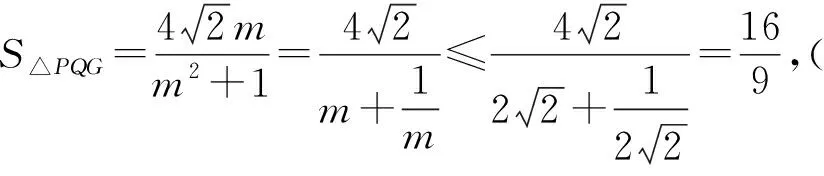
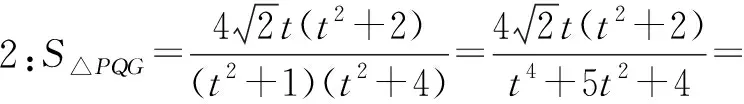
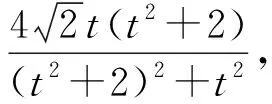
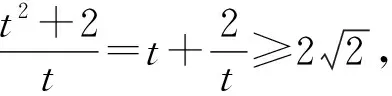
一般而言，研究二元或多元函数的问题，消元法是其中的主要方法之一，它包含直接消元和间接消元两种.直接消元就是将其中一个变量用另一个变量来表示，特别要注意的是被消去变量的范围要转移给留下来的变量；间接消元就是引进第三个变量来表示原有的变量，便于沟通之间的关系，常见的有三角换元、均值换元等.对于单变量函数的最值问题，导数法是有效手段之一，除此之外还可根据式子结构的特征，采用不等式的方法求解.

反观上述解题过程，可以发现思路易得，运算不易，主要原因在于直接运算繁琐，字母参数多，内在联系隐晦.对于这类问题，在平时的教学中，我们要以学生的思维方式、认知心理为教学起点，让教师的思维顺应或契合学生的思维，才能使教的过程和学的过程融入一体.不仅要注重思路分析，更要手把手地亲身示范，带领学生一起经历障碍突破的过程，才能培养学生不畏艰难困阻的自信心，提高学生的理解能力、运算能力和思维能力.

新一轮课程改革已经拉开帷幕，核心素养理论指导下的数学课堂教学应如何进行？学生的思维能力怎样才能得到更好培养？我认为，核心素养下的数学课堂应循着学生的思维轨迹，让学生不断地产生“冲突”，思考“冲突”，化解“冲突”.从学生的视角解决问题，不仅能让学生“知其然”，还能“知其所以然”.如果不考虑学生已有的认知，一味地将自己的想法强加给学生，那么课堂探究只能流于形式，不仅不能促进学生数学思维的发展，反而会对他们的思维发展起到负面影响.数学知识是学生自己建构的，数学教学应为学生有效自主建构而教.因此，数学教师要营造学生自主建构知识的氛围与条件，遵循学生的思维特性，只有以学生的思维为起点设计教学活动，指导建构数学知识的策略与方法，才能引起学生思维的共鸣，让学生建构起自己的数学理解，真正达到发展数学思维的目的.