初中数学毕业考试命题变革的思考与实践

吴增生

(浙江省仙居县教育局教研室 317300)

初中数学毕业考试是对学生初中阶段学习结果的终结性评价，同时兼顾升学选拔功能,对数学教育教学具有重要的导向作用.当前，初中学业水平考试还存在着价值趋向不一致，试题质量不够高等问题.基于此，教育部于2019年发布了《关于加强初中学业水平考试命题工作的意见》(下文简称《意见》)，提出了坚持正确导向，提高命题质量等一系列要求，明确了今后命题改革的基本方向.以这一《意见》为导向，分析当前初中毕业考试命题的不足，提出研究改进命题的可操作的方案，并进行实践研究，这具有重要的理论和现实意义.

1 初中毕业考试的现状和存在的问题

自从本世纪初第一轮课程改革以来，学业考试评价也经历了近20 年的改革，全国各地的毕业考试的价值取向发生了根本性的变革，命题技术得到了长足的发展，为促进教学方式的变革，保障新课程的实施做出了积极的贡献.主要体现为：(1)考试的根本属性从选拔性常模参照评价转变为标准参照评价兼顾升学选拔要求；(2)从原来只重视结果性知识转变结果与过程并重，重视知识形成过程中数学思想方法的考核，重视知识形成过程中“观察、实验、猜测、计算、推理、验证”[1]等数学活动的考核.重视知识的应用，减少了繁、难、偏、旧的传统考核内容；(3)命题技术有长足的发展.通过近20年的考试评价改革，对知识的形成过程及应用的考核技术逐步成熟.比如，创建适当的问题情境(包括数学情境、现实情境、学习情境、科学情境、社会人文情境等)考核学生对知识的理解和应用水平，用开放性、探索性试题评价学生的数学研究和问题解决能力，等等.

尽管初中数学毕业考试改革总体上是成功的，为课程改革做出了重要贡献，但是，当前命题中仍然存在一些不容忽视的问题，需要进一步地补短板和变革.

1.1 缺乏统一可操作的学业水平划分标准

教育部《关于加强初中学业水平考试命题工作的意见》指出初中学业考试必须依据课程标准科学命题.但2011版的义务教育数学课程标准，没有构建学业水平的整体分级标准，也没有提出针对具体内容学业水平的分级标准，评价建议也比较抽象，缺乏可操作性[2].这就导致了不同地区对学业水平标准的不同理解，各地考试的价值取向、难度水平的巨大差异.如果能制定全国统一的学业水平划分标准，给出命题要求和命题技术指导，制定命题的负面清单，那么，就可以进一步提高全国各地毕业考试价值取向的一致性，提高命题的质量，形成一致的教学导向，这对改进数学教学，推进课程改革，具有很好的促进作用.怎样依据课程标准，以数学学科综合素质为导向，整体构建初中数学学业水平分级标准？《普通高中数学课程标准(2017版)》给出了数学核心素养的水平划分，提出了核心素养为导向的学科质量标准[3]，教育部考试中心研发了“一体四层四翼”的高考评价体系，明确以数学“必备知识、关键能力、学科素养、核心价值”为考查目标[4]，这为建立学科综合素质导向下的初中数学学业质量标准提供了启发；王立东，杨涛,王烨晖，史宁中,宋乃庆，刘晓玫，马复等从国家义务教育质量监测视角，分析了国际国内学生学业表现能力的理论与实践，构建了国家质量监测中的五维基本学习表现能力指标体系：数学运算能力、空间想象能力、数据分析能力、推理能力、解决问题能力[5].这为构建核心素养关键能力引领下的初中数学学业水平分级标准提供了方向性引领和可参照的方案.

1.2 命题技术发展滞后于课程改革进程

随着课程改革的不断深入，数学核心素养逐步进入课程目标体系中，《义务教育数学课程标准(2011版)》用“数感、符号意识、空间观念、几何直观、推理能力、运算能力、数据分析观念、模型思想、应用意识、创新意识”[6]等核心关键词描述数学核心素养，教育部的《意见》中也明确提出重视基础知识、基本技能、思维能力、分析问题和解决问题能力、创新意识等学科综合素质考核的命题要求.意见中的这些要求，是《义务教育数学课程标准(2011版)》在考试评价上要求的具体体现，是今后学业考试命题的基本准则和改革方向.但是，当前初中毕业考试命题的双向细目表是以知识的认知维度(了解、理解、掌握)为基准，进行逐题设计，缺乏关联知识、技能、思想方法和思维活动的纽带与桥梁——学科大观念、关键能力等内容.缺乏学科大观念和关键能力的引领，试卷就可能成为缺乏思想灵魂的题目拼凑，试题的教学导向也可能出现偏颇.

1.3 当前初中数学毕业考试试题中存在的主要问题

1.3.1 函数试题出现了普遍的解析化倾向

全国各地的毕业考试试题中，以函数图象为背景，运用代数运算方法研究几何问题的压轴题出现频率很高(2019年达到80%以上)，这与函数的数学本质相违背，超越了课程标准的要求，降低了试题的效度和信度，加重了学生不必要的课业负担[7].

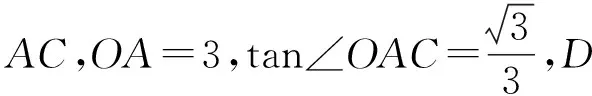
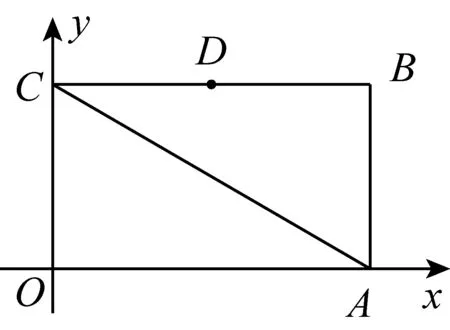
图1-1

(1)求OC的长和点D的坐标；

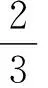
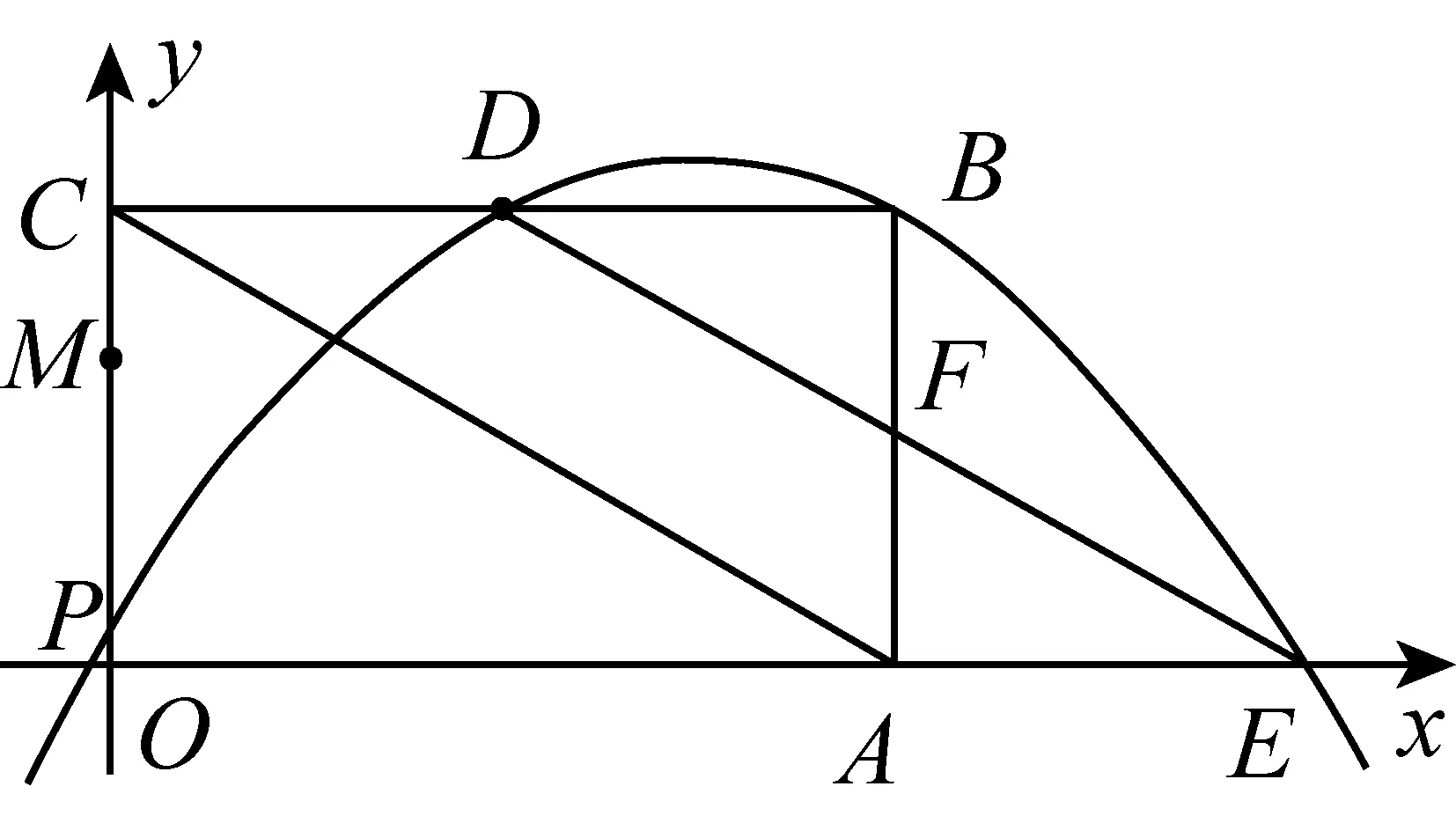
图1-2

①将△DBF沿DE所在的直线翻折，若点B恰好落在AC上，求此时BF的长和点E的坐标；

②以线段DF为边，在DF所在直线的右上方作等边△DFG，当动点P从点O运动到点M时，点G也随之运动，请直接写出点G运动路径的长.

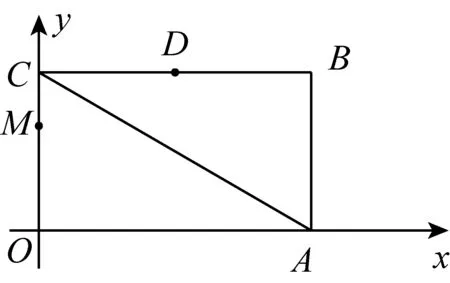
图1-3

本题与二次函数关联很少，考核函数的效度很低，事实上，去除坐标系和抛物线改编成纯几何题，试题测评几何知识及直观想象能力、逻辑推理能力的效度更高.

1.3.2 几何试题繁、难、偏现象抬头

近几年来，几何压轴题技巧性越来越强，试题拼凑，缺乏逻辑性现象比较普遍，这偏离了几何的核心育人价值，降低了几何试题评价空间观念、几何直观和推理能力的效度.初中几何内容的核心育人价值是发展学生的空间观念、几何直观以及推理能力.史宁中认为，一个简单推理是有逻辑的充要条件是这个简单推理具有传递性[8].有逻辑的几何推理应该是有序地研究几何图形，获得其属性和关系.几何试题逻辑性的具体要求是：①问题明确；聚焦研究对象；②研究具有层次性；③研究具有系统性，题干与各小题之间应该前后连贯，逻辑一致.

例2已知：MN为⊙O的直径，AB,CH是⊙O的两条弦，AB⊥OE于D，CH⊥MN于点K，连接HN,HE.HE与MN交于点P.

(1)如图2-1，若AB与CH交于点F,求证：∠HFB=2∠EHN;

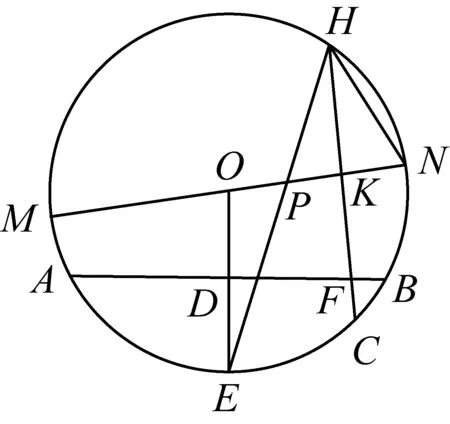
图2-1

(2)如图2-2，连接ME,OA.OA与ME交于点Q,若OA⊥ME,∠EON=4∠CHN,求证：MP=AB；

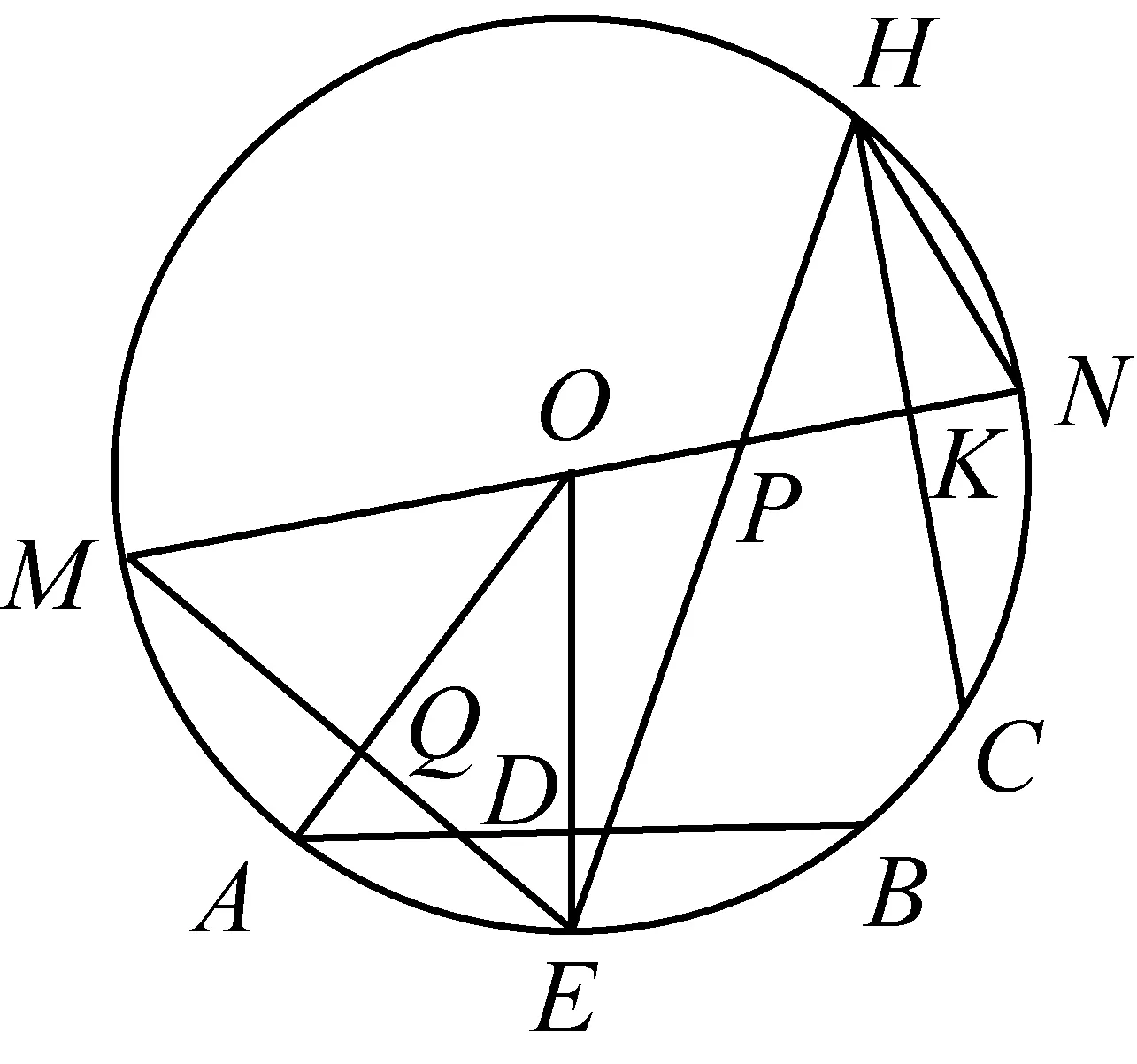
图2-2

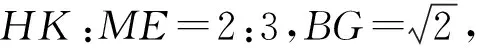
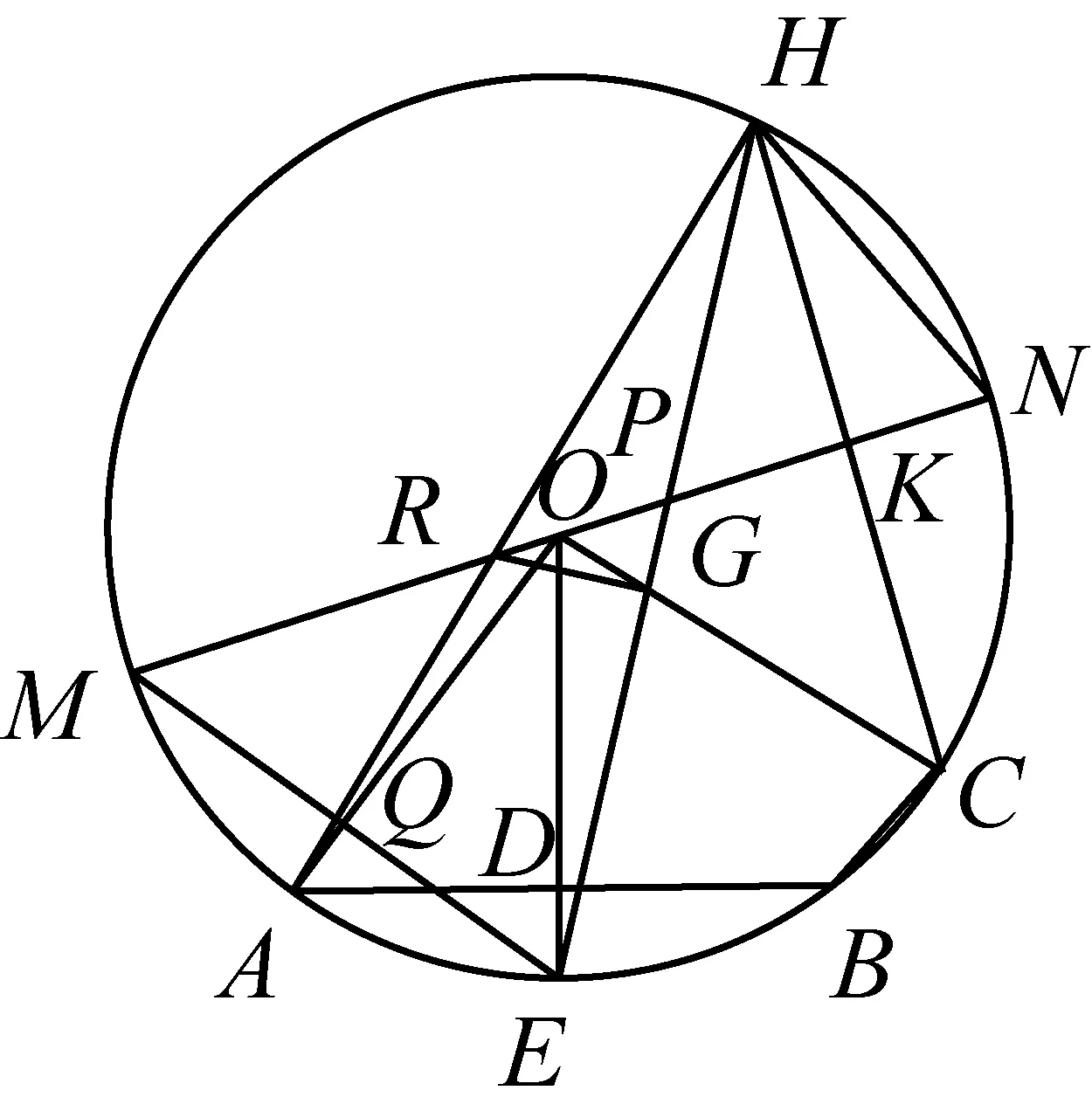
图2-3

本题中，研究对象不聚焦，第(1)小题研究的是∠HFB与∠EHN关系，第(2)小题研究线段MP，AB的关系，第(3)小题又求线段RG的长，小题之间没有必要的逻辑关联，图形繁杂，令人厌烦，没有体现几何问题本来应有的“图形简约，内涵深刻，具有美感，引人入胜”的特点，偏离了几何的核心育人价值，降低了试题测评空间观念、几何直观和逻辑推理能力的效度和信度.

1.3.3 统计与概率试题出现了许多只计算统计量的“伪”统计题

统计与概率内容的核心育人价值是发展学生的数据分析观念，所谓数据分析观念指的是：

“了解在现实生活中有许多问题应当先做调查研究，收集数据，通过分析做出判断，体会数据中蕴涵着信息；了解对于同样的数据可以有多种分析的方法，需要根据问题的背景选择合适的方法；通过数据分析体验随机性，一方面对于同样的事情每次收集到的数据可能不同，另一方面只要有足够的数据就可能从中发现规律.数据分析是统计的核心”[9].

但是，各地的统计概率试题中，简单计算、填空、填图而没有数据分析的“伪统计”试题依然存在，例如“数据2，7，5，7，9的众数是▲．”，等等.

2 怎样的试卷和试题是好的试卷和试题

2.1 怎样的试卷是好试卷

毕业考试的目的是评价学生经过初中阶段学习后对课程标准中学习要求的达成度，因此评价试卷质量的根本标准在是：它是否有效、可靠地评价了学生的数学学业水平.这可以用教学评价中的效度、信度、区分度等指标来分析.保证试卷的效度和信度各有一些命题要求，如为了保证效度，需要提高试卷的适标性、自洽性、思想性等；为了保证信度则要做到试题的科学性、表述通俗易懂简洁无歧义，等等.以课程标准为依据，能力立意，重视数学思想和方法，这是一份试卷的灵魂，也是保证试卷整体效度的需要.

2.2 怎样的试题是好试题

试题是试卷的最小独立组成部分，怎样的试题是好的试题呢？首先要消除以下两种误解：一是认为好试题一定是难题，二是认为好试题一定是考核内容多，知识综合的题.

(1)试题的有效性与可靠性.能从学生的解题过程中比较可靠地推断出学生的真实知识技能及关键能力水平的试题就是好试题，这可以用教育评价学的效度、信度、区分度等指标来分析.

(2)试题的教育性.试题的教育性指的是试题可以作为重要的资源进行教学，并能获得好的育人价值.这就要求试题“关注本质、表述简约、内涵深刻、具有美感、引人入胜”，那种表述繁杂、牵强拼凑、结构凌乱、令人厌烦的试题就不是好试题.具有发展性，能从试题出发生成一系列具有创新研究价值的问题，这是试题教育性的重要标志.

(3)试题的教学导向性.所谓教学导向性指的是试题考核内容及要求对师生教和学行为的导向作用.数学学业考试应该导向教师积极探索基于情境、问题导向、深度思考、高度参与的教育教学方式,引导学生自主、合作、探究学习，理解数学本质,导向提高学生综合素质.这也是教育部《意见》的要求.

3 学科综合素养导向下的初中毕业考试命题实践

3.1 借鉴学科素养的“三会”概括解释，融合“四基”“四能”，整体划分初中数学学业水平

史宁中给出数学学科核心素养的概括解释“用数学的眼光观察世界、用数学的思维思考世界、用数学的方式表达世界”[10]，喻平在此基础上把核心素养分成知识理解、知识迁移、知识创新三级水平[11].借鉴《普通高中数学课程标准(2017年版)》中学业质量标准及及国家义务教育质量监测的学业表现力五维结构(见文献[5])，以关键能力为纽带，融合“四基”“四能”，以“情境与问题”、“思维与表达”、“交流与反思”三个维度为顶层架构划分出三级学业水平.水平一、二、三分别对应着合格、良好和优秀等级.这三个维度既对应着数学学科素养中的“三会”，也对应着“四能”,还融合进了国家义务教育质量监测的学业表现力五维要素.“情境与问题”对应着通过数学直观想象与抽象观察客观世界，也对应着引入研究对象，理解、发现和提出数学问题；“思维与表达”对应着数学推理、运算和建模等数学思维活动过程，也对应着分析问题和解决问题的过程；“交流与反思”则对应着用数学的方法进行反思交流，也对应着解决问题后的反思总结.

水平一：

①情境与问题.能够在熟悉的情境中理解数学概念、规则、符号、模型，理解数学问题的背景及其数学表达.能在熟悉的问题情境中通过观察、想象和抽象发现数量和数量关系，几何图形及其关系，通过归纳发现和提出熟悉的数学命题.理解字母表示数的意义，能在熟悉的情境中了解数、代数式、方程、不等式、函数的实际背景及其数量关系的符号表示，明确其研究的核心问题;会阅读一次函数、二次函数、反比例函数图象，了解变量的依赖关系和变化规律；能从熟悉的实物中发现和理解几何图形及其关系，理解几何概念、性质及判定，会区分几何中熟悉命题的条件和结论，能通过类比和归纳的方法从熟悉的情境发现几何中熟悉的命题；会想象图形的变化过程，理解用坐标刻画图形的位置及其变化的方法；知道数据分析的过程，能收集和整理数据，会阅读简单的统计图表，会辨别不同的统计量，知道概率的意义.

②思维与表达.会借助数学符号、图表、概念、规则和模型理解数量和数量关系、几何图形及其关系，会进行简单的运算和推理，能模仿已学的解题过程分析和解决熟悉情境中简单的数学问题.会用已学的运算法则、运算律和公式按照要求进行简单的数与代数式的运算(运算不超过3步)、解方程(数字系数一元一次方程、二元一次方程组、可化为一元一次方程的分式方程)和解不等式(数字系数一元一次不等式(组)，会通过字母表示数把数量关系推广到一般，通过符号运算获得数量关系的一般规律；能证明课程标准中要求证明的重要几何定理，会应用基本事实、定理、推论在熟悉的情境中进行简单的推理和计算(不超过5步，两个“大前提、小前提、结论”循环)；会计算简单的统计量(平均数、中位数、众数、方差)，会用简单枚举方法求随机事件的概率.

③交流与反思.能模仿例题的解题过程有条理地书写解题过程，并通过反思和总结判断思考过程的合理性，通过交流体会解题的通性通法.

水平二：

①情境与问题.能在关联的情境中抽象出数学概念、规则、符号和模型，并进一步发现和提出简单的数学问题.能通过函数解析式及其图象理解一次函数、二次函数、反比例函数的性质，能通过具体例子理解一次函数、一次方程及一元一次不等式之间的关系；能从关联的情境中抽象几何概念、几何图形及其关系的性质和判定，能根据文字命题画出图形、写出已知求证，能在想象图形结构及其变化过程的基础上，借助图形结构及其变化理解几何概念和命题、发现和提出熟悉的几何命题；能根据现实背景提出简单熟悉的数据分析问题，能在具体实例中理解不同的统计图表和统计量的特点，会借助概率的意义理解用列表法和画树状图法求古典概型概率的原理，能通过具体实例体会数据的随机性.

②思维与表达.会借助数学符号、图表、概念、规则和模型表示数量和数量关系、几何图形及其关系，能用符号运算、逻辑推理和数学建模的方法分析和解决关联情境中的数学问题.能根据运算对象选择合理的算法进行数、代数式的准确运算，能说明运算的依据；能熟练地解数字系数一元一次方程、一元二次方程、可化为一元一次方程的分式方程、二元一次方程组及一元一次不等式(组)，能用代数式、方程、不等式、函数模型分析和解决关联情境中的问题，研究一般规律；理解互逆命题，能通过归纳、类比和逆向思考的方法提出新命题，并能用演绎推理方法加以证明.能用自然语言、图形语言、符号语言和坐标表示图形及其变换的性质(坐标法只要求表示多边形顶点位置及其课标中特定的轴对称、平移、中心对称、位似变换的顶点坐标关系).能根据数据的背景选择适当的统计量分析数据，能用列举法求简单随机事件的概率.

③交流与反思.能读懂他人的解题过程，能独立、有条理地书写解题过程，能解释解题过程的依据，反思和总结解题过程的思想方法.

水平三：

①情境与问题.能在陌生和综合的情境中抽象出数学概念、规则、符号和模型，引入研究对象，发现和提出新的数学问题.能从解析式和图象两个角度阐释函数的性质，从变化过程、数和形三方面阐述一次函数、一次方程、一元一次不等式之间的联系，并能通过类比推广到一般，能从大小、运算和对应关系出发提出数量关系方面的研究问题；理解从背景到几何概念到命题体系的局部逻辑结构，能通过类比和归纳的方法系统提出一类几何图形研究的问题系列，能用统一的思想和方法抽象出几何图形的研究思路、研究内容、研究方法，整理研究结果，理解几何图形的概念指的是什么、几何图形的性质指的是什么、几何图形特例和关系的判定指的是什么，抽象出三角形、四边形、圆等内容的知识体系，能用统一的思想和方法抽象出三角形的全等与相似的知识体系以及图形的轴对称、平移和旋转(包括中心对称)的知识体系；能阐释不同统计图和统计量的含义、特点和差异，能举例说明数据的随机性.

②思维与表达.能综合运用数学符号、图表、概念、规则和模型适当地表示数量和数量关系、几何图形及其关系，能综合运用符号运算、逻辑推理和建立模型的方法分析和解决新的综合情境中的问题.会综合运用运算法则和运算律，选择和综合应用算法对符号进行准确运算，并能阐述算理，理解算法背后的数学思想，能建立代数式、方程、不等式、函数的综合模型(如简单的分段函数模型，函数方程不等式整合模型等)解决新情境中的问题；能独立研究一类几何图形及其关系，基于图形变换的观点，运用联想、类比、归纳和演绎的方法提出新的命题，能运用演绎推理的方法建立命题之间的局部逻辑体系，能借助图形结构及其变化表示数学问题，用“前推法”“后推法”和“两头凑”法分析解决问题的思路；掌握用样本估计总体的方法，能根据数据背景综合和创新数据分析方法分析数据，做出判断和决策.

③反思与交流.能总结数与代数式、方程、不等式研究的核心思想和方法——符号(包括模型)抽象、符号运算和推理；函数研究的思想和方法——建模模型表述变化过程，用数形结合的方法及符号运算和推理的方法研究变化过程;图形与几何研究的思想和方法——几何图形及其关系的抽象，直观想象和逻辑推理；数据分析的核心思想方法——根据问题背景选择适当的数据分析方法，通过随机抽样和样本估计总体方法，基于用频率估计概率分析和把握随机现象的规律.能通过总结和交流，体会抽象、推理、模型三种基本数学思想的作用和思考步骤，总结分类讨论、数形结合、特殊化与一般化、数学转化、数学建模、类比、归纳、几何变换等思想方法有什么用、怎样用和注意要点，并能迁移到新的情境.

3.2 制作融合知识、思想方法和关键能力的双向细目表

在上述学业水平划分的基础上，结合拟考核内容,规划不同关键能力在试题中的分布，制作包含知识内容、思想方法、关键能力及水平要求的双向细目表[12].依据义务教育数学课程标准，参照高中质量标准体系和国家义务教育质量监测的做法，把初中数学的关键能力分为：符号抽象(包括建立数、代数式、方程、不等式、函数等模型抽象)能力、逻辑推理能力、数学运算能力、直观想象能力(空间观念、几何直观、数形结合能力)、数据分析能力以及这些能力融合后形成问题解决的能力.关键能力的中、低水平考核可以在简单题、中等难度试题中安排落实,高水平的关键能力体现在综合性试题中，往往用问题解决类型的试题来体现.基于双向细目表，整体规划、分类实施，综合考查学生的基础知识、基本技能、数学思想方法和数学关键能力，评价学生的整体学业水平.

例如：本次命题中的部分细目表(数与代数领域)如表1(试卷实测总体难度0.746，数与代数领域实测难度0.75)：

3.3 基于学科大观念构建不同知识领域的命题主线

大观念(big ideas )指的是组织某一领域核心概念、原理、思想方法和解决问题方法的顶层观念和思想[13],也是对知识形成、发展和应用过程所反映的思想方法的再概括[14]，认知科学研究表明，大观念对于组织知识体系，形成解决问题策略具重要导向作用，David Niemi, Julia Vallone, Terry Vendlinski(2006)研究了用数和方程的大观念(运算与运算律，等式性质)引领下的美国七年级学生的代数学业水平评价研究，形成了系列的研究成果[15].分析初中数与代数、图形与几何、统计与概率不同领域的大观念，形成相应的命题主线，不仅可以明确相关领域的核心知识，而且可以基于知识的发生发展和应用过程命制出能有效评价学生“四基”“四能”的好试题，真正把学科综合素质的评价落实到毕业考试中.

3.3.1 数与代数领域的命题——以符号抽象、运算、推理和数形结合为主线

数学是研究数量关系、空间形式的一门科学.数学源于对现实世界的抽象，基于抽象结构，通过符号运算、形式推理、模型建构等，理解和表达现实世界中事物的本质、关系和规律[16].《义务教育数学课程标准(2011版)》对数与代数领域提出的课程总目标是：体验从具体情境中抽象出数学符号的过程，理解有理数、实数、代数式、方程、不等式、函数；掌握必要的运算(包括估算)技能；探索具体问题中的数量关系和变化规律，掌握用代数式、方程、不等式、函数表述的方法[17].这些课程总目标，本质上是符号抽象(包括建立模型)、运算和推理的过程以及用数形结合思想研究函数的变换规律和变化趋势过程.因此，以“符号抽象、运算与推理”为主线命制考核数与代数领域的关键能力，具有知识领域针对性，可以提高试题评价特定领域关键能力的效度.另外，借助平面直角坐标系，利用函数图像，直观地研究函数性质，这体现了课程标准中对几何直观的要求，也是直观想象这一关键能力在函数研究过程中的体现.具体做法是：在符号抽象、符号运算、符号推理、数形结合四个维度设置考核不同水平的试题，达成对关键能力考核.

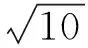
A．2和3之间 B．3和4之间

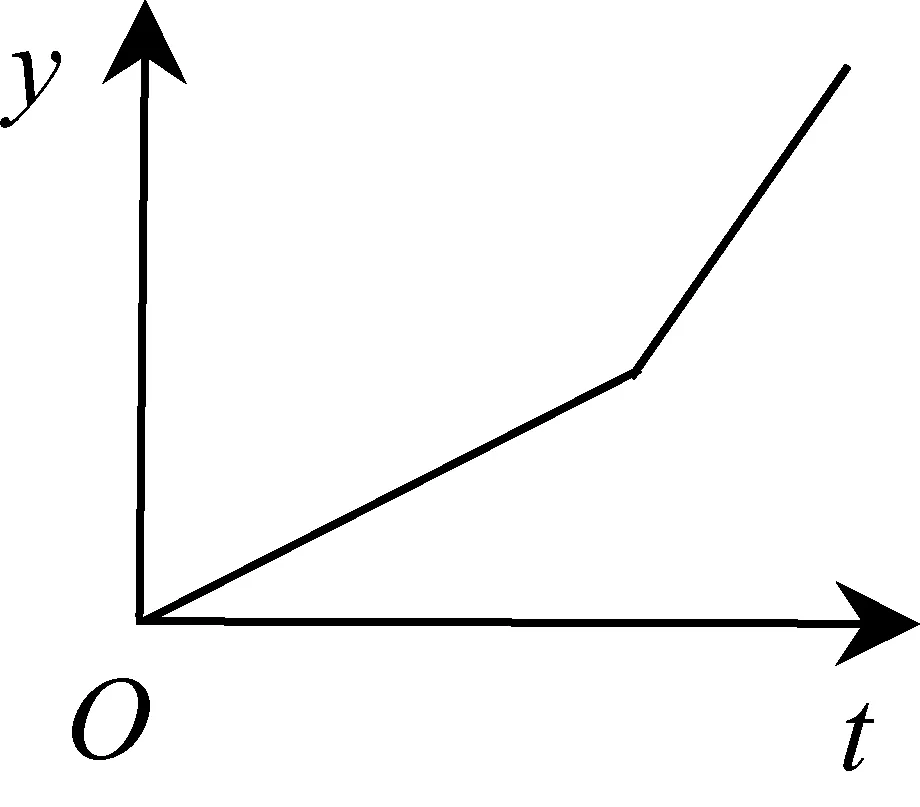
B

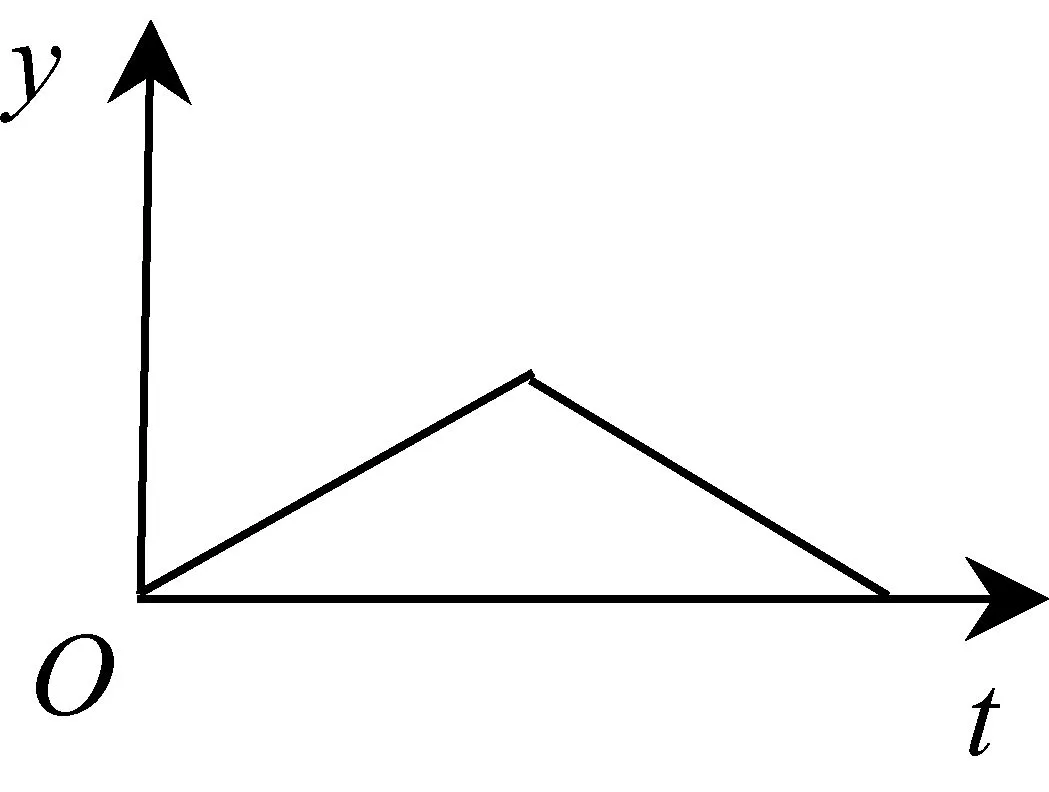
A

C．4和5之间 D．5和6之间

D

C

本题考核对用有理数估计无理数的大小，考核数学运算(估算)能力，属水平2.

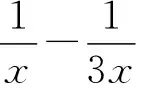
本题考核分式内容中的符号运算能力，属水平1.

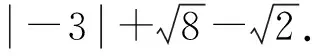
本题考核数学运算能力，属水平2.

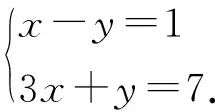
本题考核解二元一次方程组中的消元思想，考核符号运算能力，属水平2.

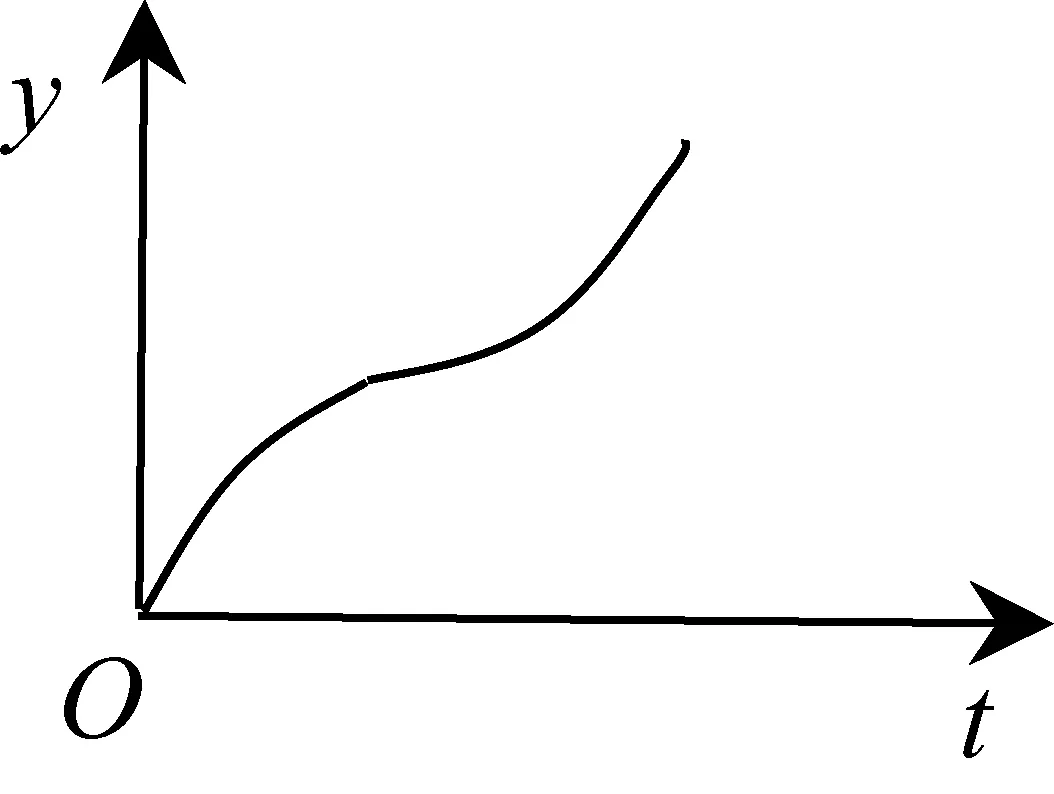
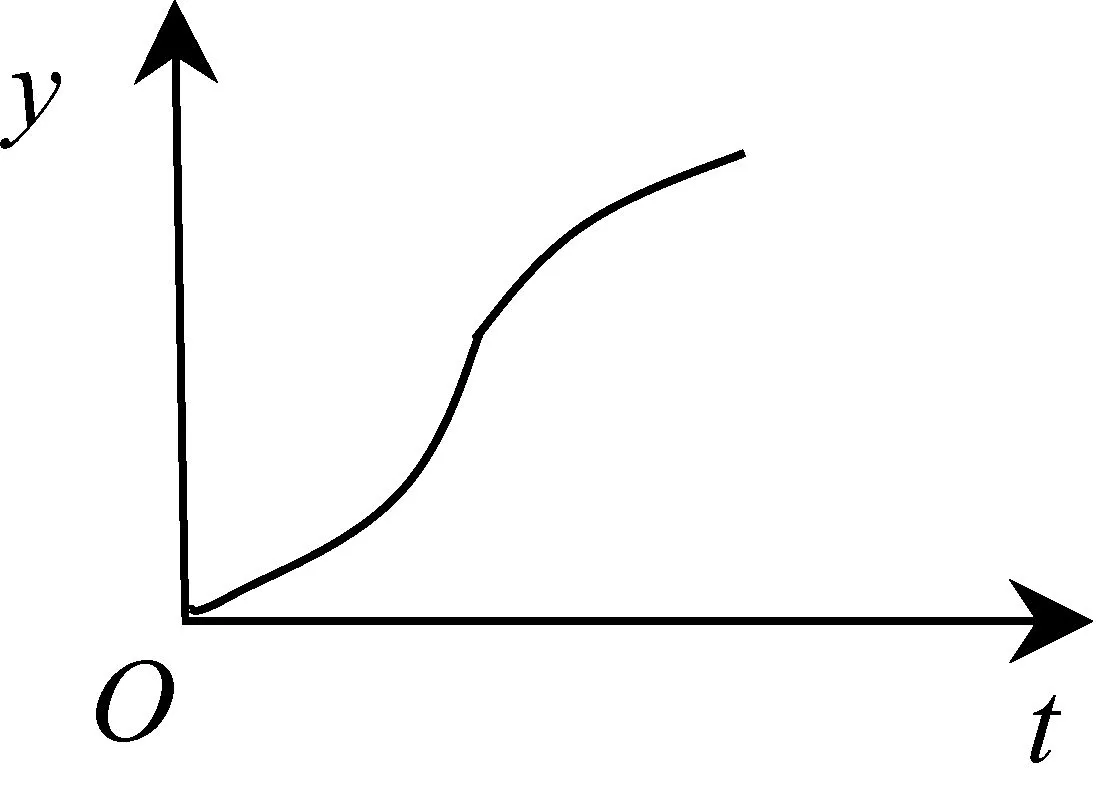
例7如图3-1，小球从左侧的斜坡滚下，到达底端后又沿着右侧斜坡向上滚，在这个过程中，小球的运动速度v(单位：m/s)与运动时间t(单位：s)的函数图象如图3-2，则该小球的运动路程y(单位：m)与运动时间t(单位：s)之间的函数图象大致是( ▲ ).

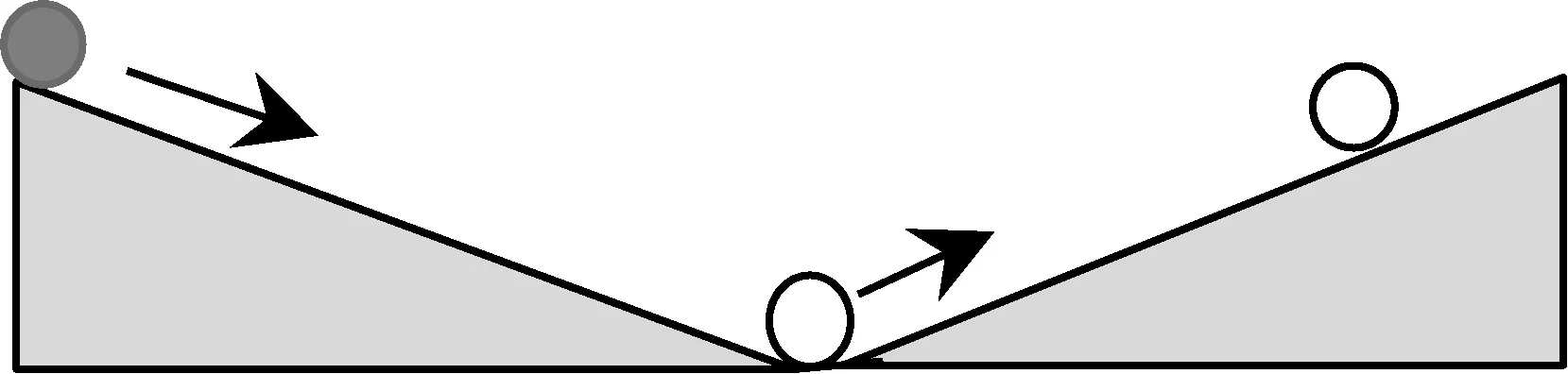
图3-1

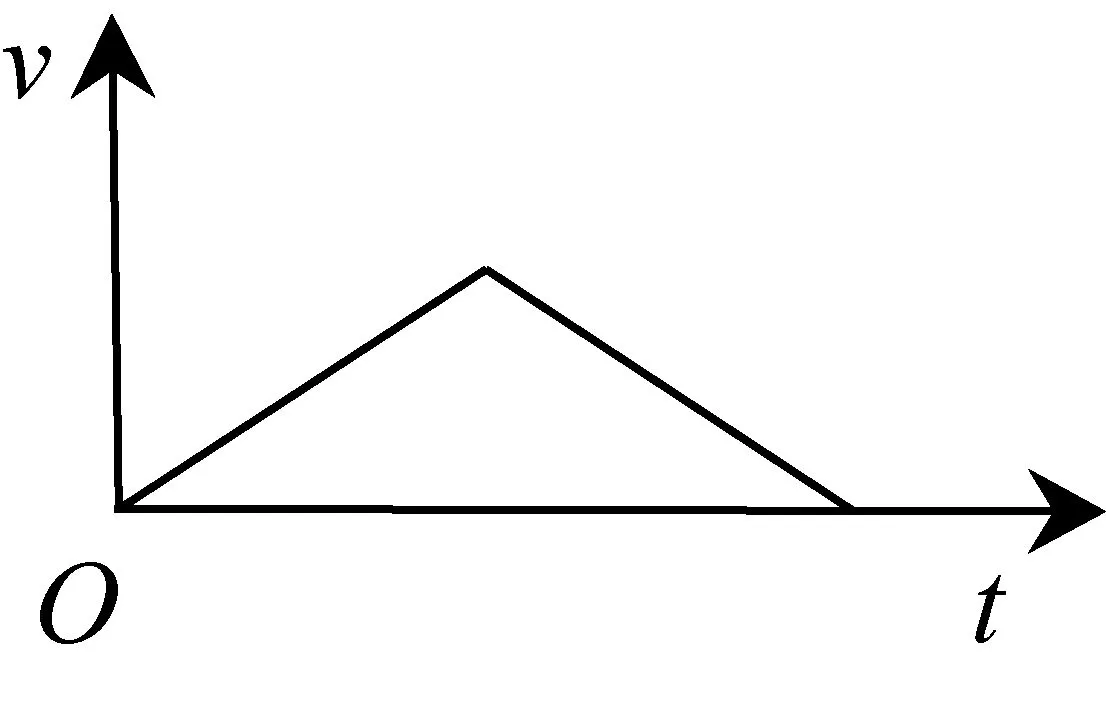
图3-2

本题考核借助图象理解函数的变化趋势和变化规律，考核直观想象能力，属水平3.

例8小明同学训练某种运算技能，每次训练完成相同数量的题目，各次训练题目难度相当．当训练次数不超过15次时，完成一次训练所需要的时间y(单位：秒)与训练次数x(单位：次)之间满足如图4所示的反比例函数关系．完成第3次训练所需时间为400秒．

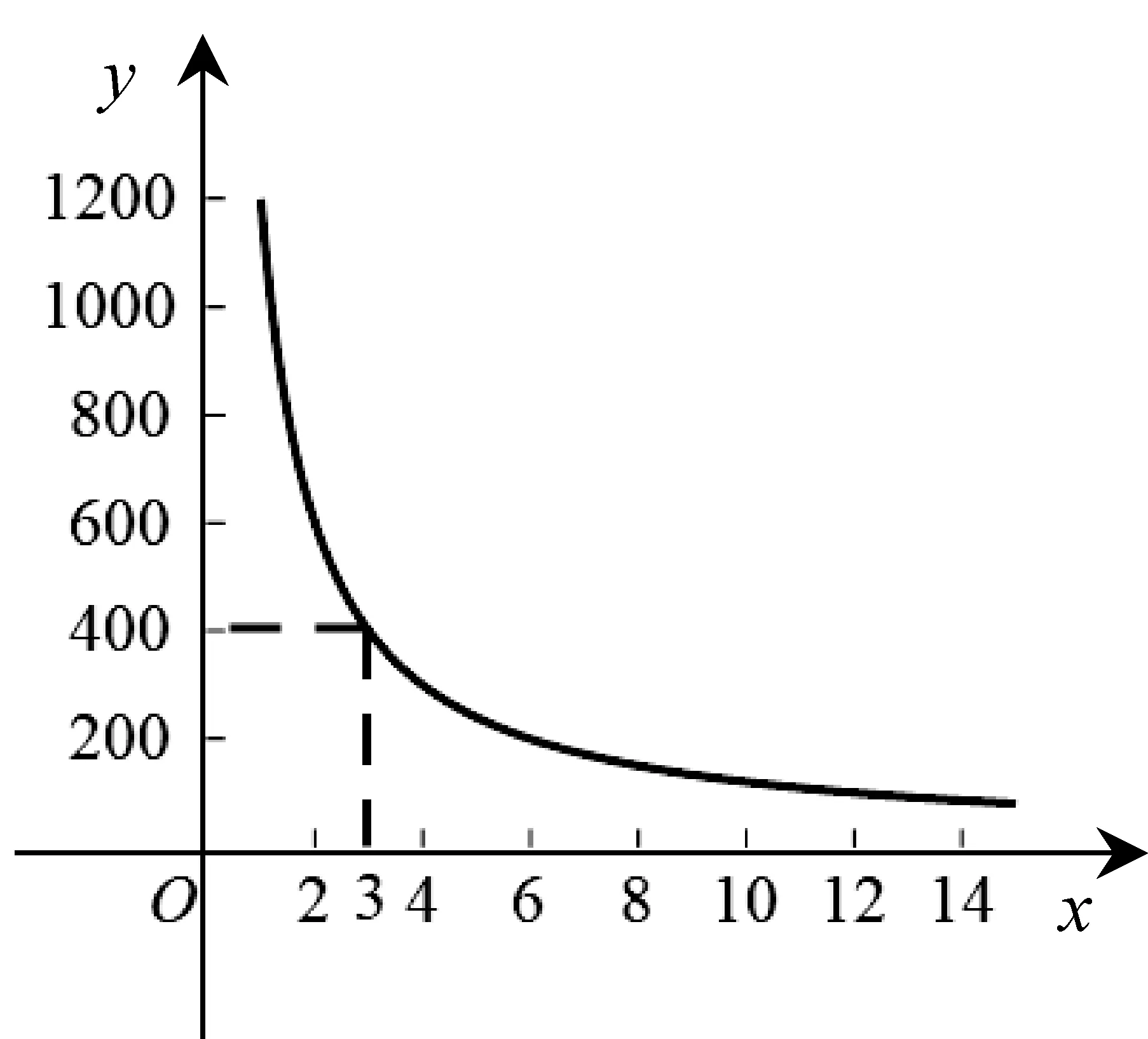
图4

(1)求y与x之间的函数关系式；

(2)当x的值为6，8，10时，对应的函数值分别为y1，y2，y3，比较(y1-y2)与(y2-y3)的大小：y1-y2▲y2-y3.

本题考核建立反比例函数模型解决问题中的符号抽象、运算和推理能力，属水平2.其中第(2)问学生可以直接计算结果比较也可以依据变化趋势来比较，考核根据图象直观理解变化趋势的直观想象能力，属水平2.

例9用各种盛水容器可以制作精致的家用流水景观(如图5-1)．

图5-1

科学原理：如图5-2，始终盛满水的圆柱体水桶水面离地面的高度为H(单位：cm)，如果在离水面竖直距离为h(单位：cm)的地方开大小合适的小孔，那么从小孔射出水的射程(水流落地点离小孔的水平距离)s(单位：cm)与h的关系为s2=4h(H-h)．

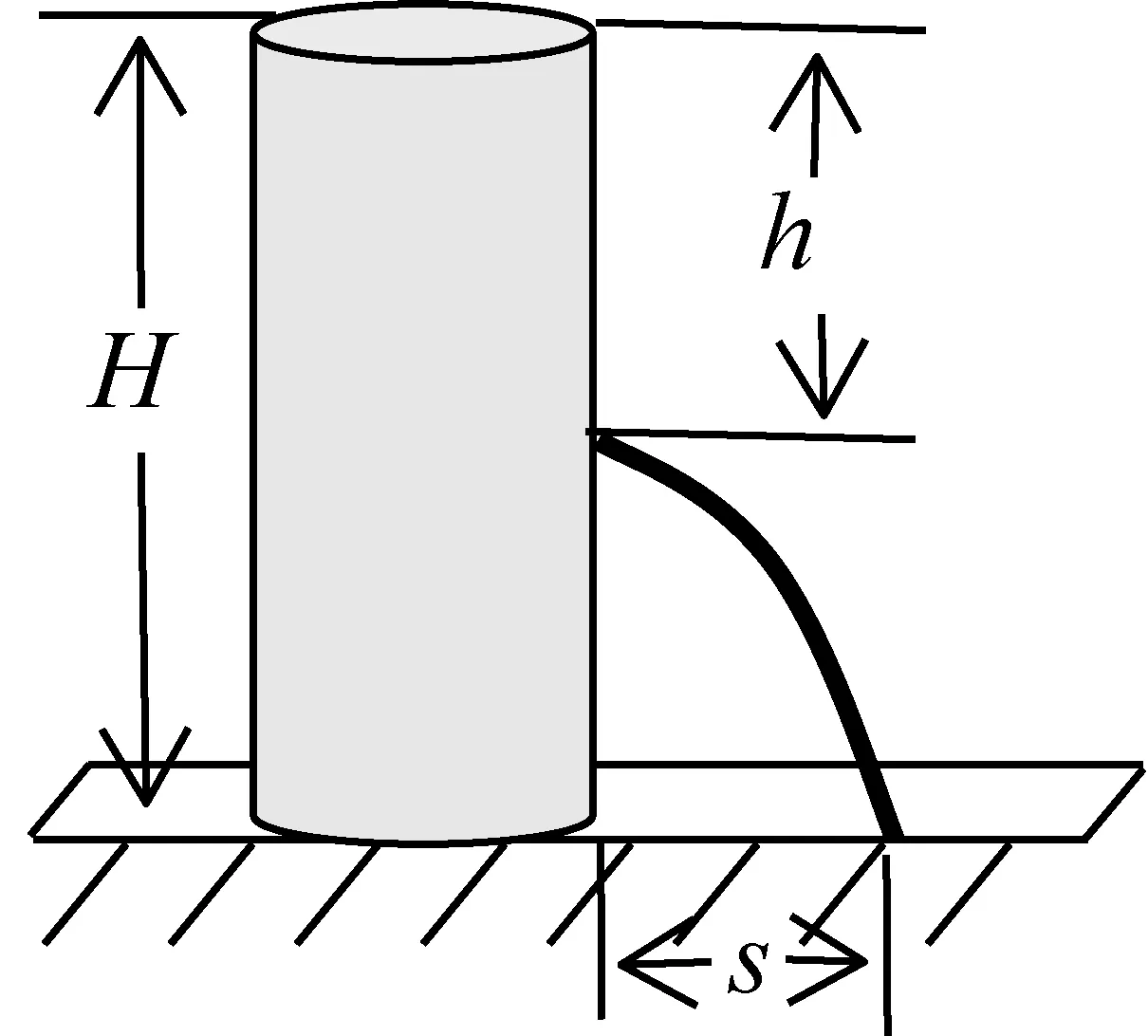
图5-2

应用思考：现用高度为20 cm的圆柱体塑料水瓶做相关研究.水瓶直立地面，通过连续注水保证它始终盛满水，在离水面竖直距离hcm处开一个小孔.

(1)写出s2与h的关系式；并求出当h为何值时，射程s有最大值，最大射程是多少？

(2)在侧面开两个小孔，这两个小孔离水面的竖直距离分别为a，b，要使两孔射出水的射程相同，求a，b之间的关系式；

(3)如果想通过垫高塑料水瓶，使射出水的最大射程增加16 cm，求垫高的高度及小孔离水面的竖直距离．

本题以跨学科问题解决的形式考核学生符号抽象、建立模型、符号运算与推理、直观想象等综合能力. 本题(1)考核理解和建立函数模型的能力，通过符号运算利用函数图象解决问题的能力，属水平3；本题(2)考核符号运算和推理能力，直观想象能力，属水平3；本题(3)考核抽象符号(设未知数)，建立函数模型的能力和基于抽象符号进行运算推理的能力，其中隐藏着分类讨论，属水平3.

3.3.2 图形与几何领域的命题——以直观想象和逻辑推理为主线

《义务教育数学课程标准(2011版)》对空间与几何的课程总目标是：探索并掌握相交线、平行线、三角形、四边形和圆的基本性质与判定，掌握基本的证明方法和基本的作图技能；探索并理解平面图形的平移、旋转、轴对称；认识投影与视图；探索并理解平面直角坐标系及其应用[18].

自从菲利克茨·克莱因提出用变换群来分类经典几何学以来，变换观点在几何研究中被普遍接受.2011版的课程标准明确地提出了图形变化的课程目标，而且，图形变换是直观想象能力中感知空间图形的位置及其变化的直接体现，也是用变换观点理解欧几里得几何的重要思想方法.因此，在图形与几何领域的考试命题中，聚焦图形结构、图形变换设计情境命制试题，聚焦研究对象，重在研究图形的构成要素与相关要素的关系，进行前后连贯、逻辑一致的设问，这是命制图形与几何领域试题的重要策略.

例10如图6，把△ABC先向右平移3个单位，再向上平移2个单位得到△DEF，则顶点C(0，-1)对应点的坐标为( ▲ ).

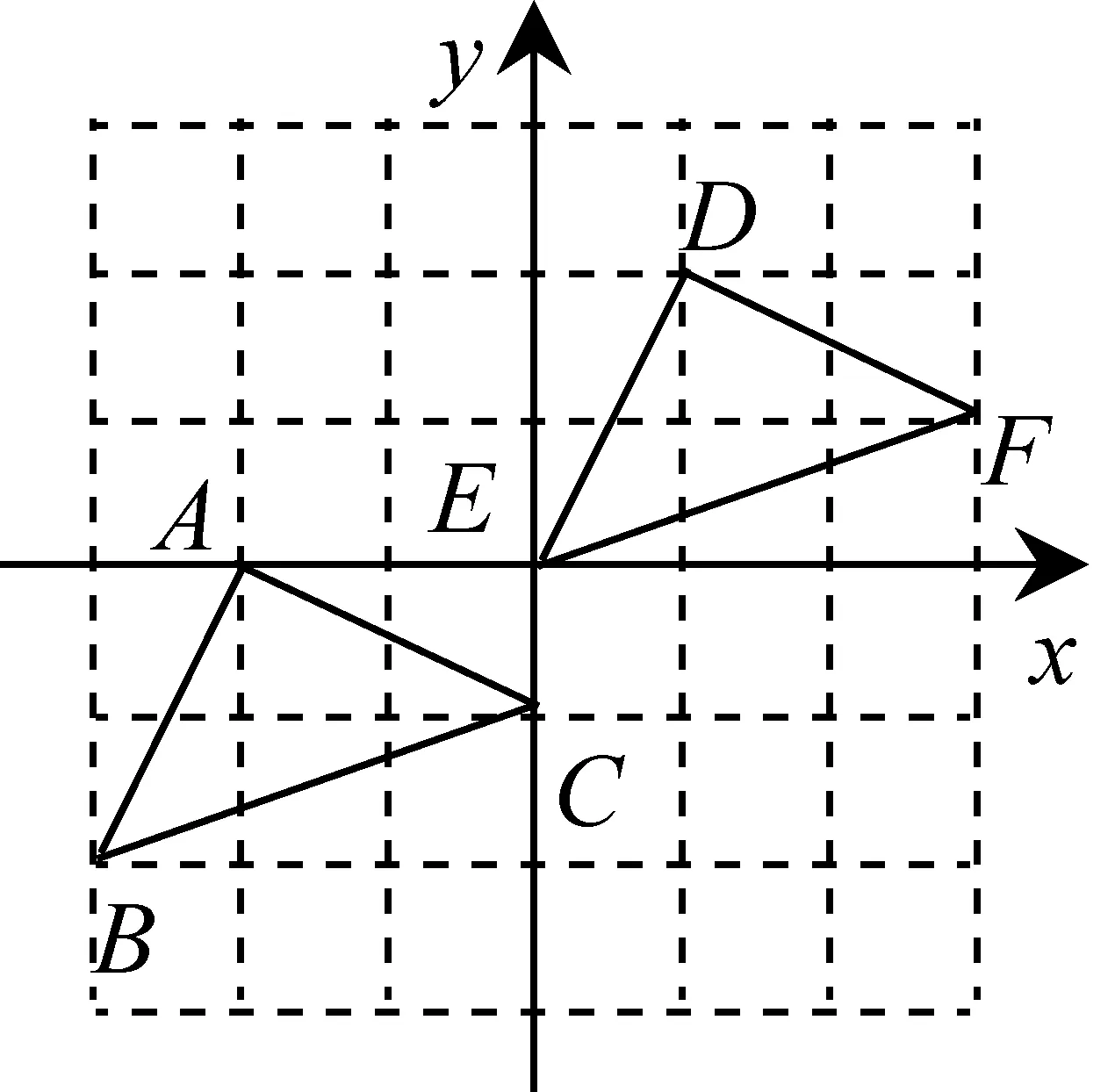
图6

A．(0，0) B．(1，2)

C．(1，3) D．(3，1)

本题考核用坐标表示平移，考核直观想象能力，属水平1.

例11下面是关于某个四边形的三个结论：①它的对角线相等；②它是一个正方形；③它是一个矩形．下列推理过程正确的是( ▲ ).

A．由②推出③，由③推出①

B．由①推出②，由②推出③

C．由③推出①，由①推出②

D．由①推出③，由③推出②

本题在矩形、正方形知识背景下创设演绎推理情境，考核演绎推理的逻辑性，属逻辑推理水平3.

例12把一张宽为1 cm的长方形纸片ABCD折叠成如图7所示的阴影图案，顶点A，D互相重合，中间空白部分是以E为直角顶点，腰长为2 cm的等腰直角三角形，则纸片的长AD(单位：cm)为( ▲ ).

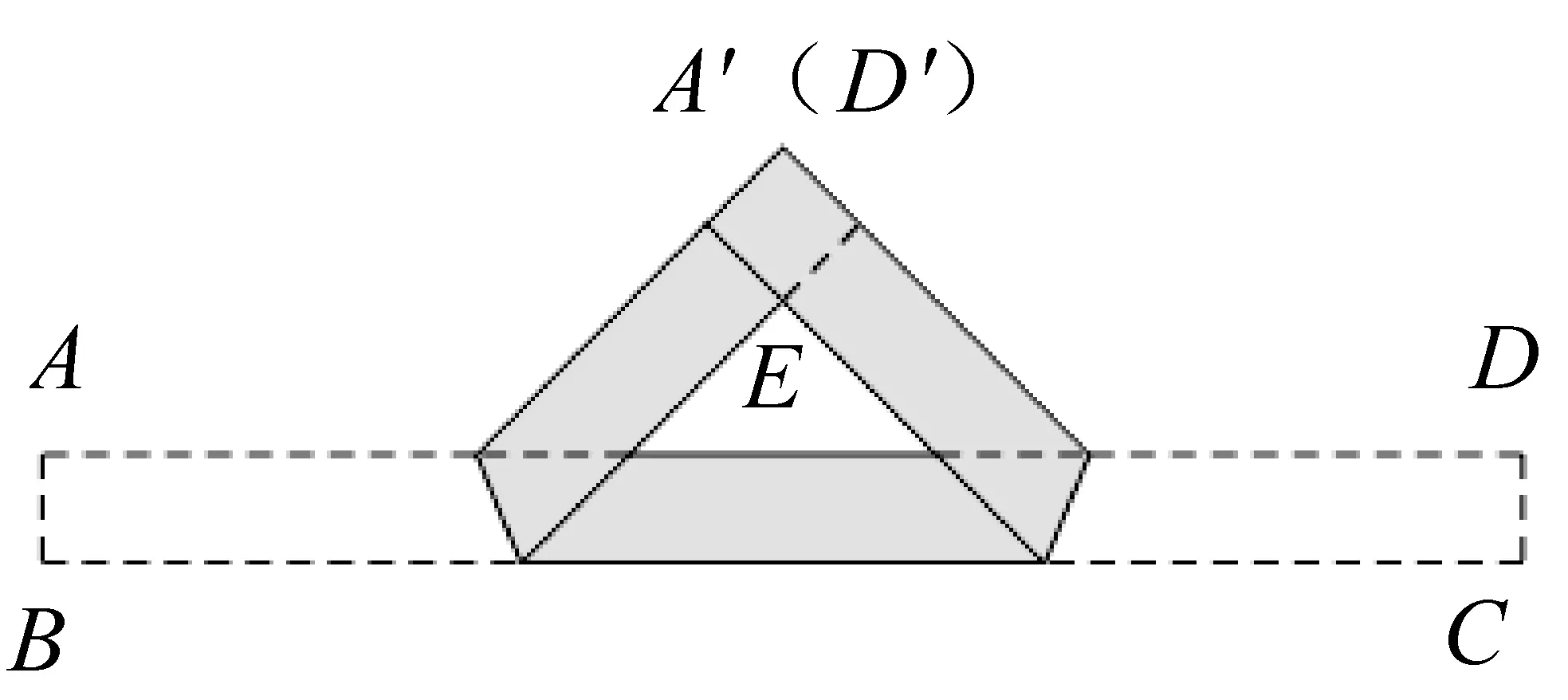
图7

本题考核平行线、直角三角形、矩形、轴对称知识的应用及直观想象和推理运算能力，属水平3.

例13用四块大正方形地砖和一块小正方形地砖拼成如图8所示的实线图案，每块大正方形地砖面积为a，小正方形地砖面积为b．依次连接四块大正方形地砖的中心得到正方形ABCD，则正方形ABCD的面积为▲(用含a，b的代数式表示)．

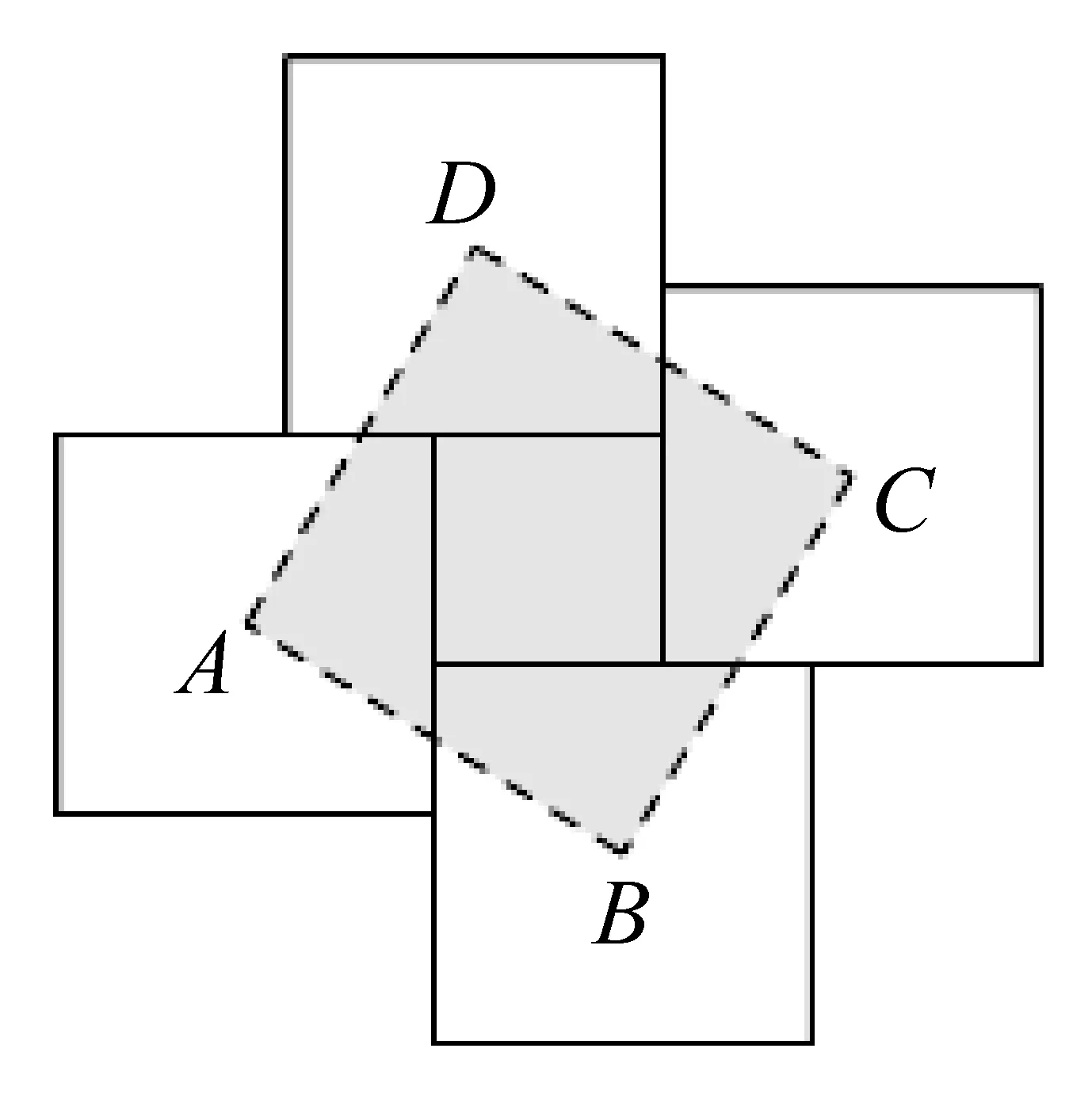
图8

本题以毕达哥拉斯地砖为背景，考核图形的旋转，全等三角形、正方形相关知识，直观想象和推理运算能力，属水平3.

例14如图9，已知AB=AC，AD=AE，BD和CE相交于点O.

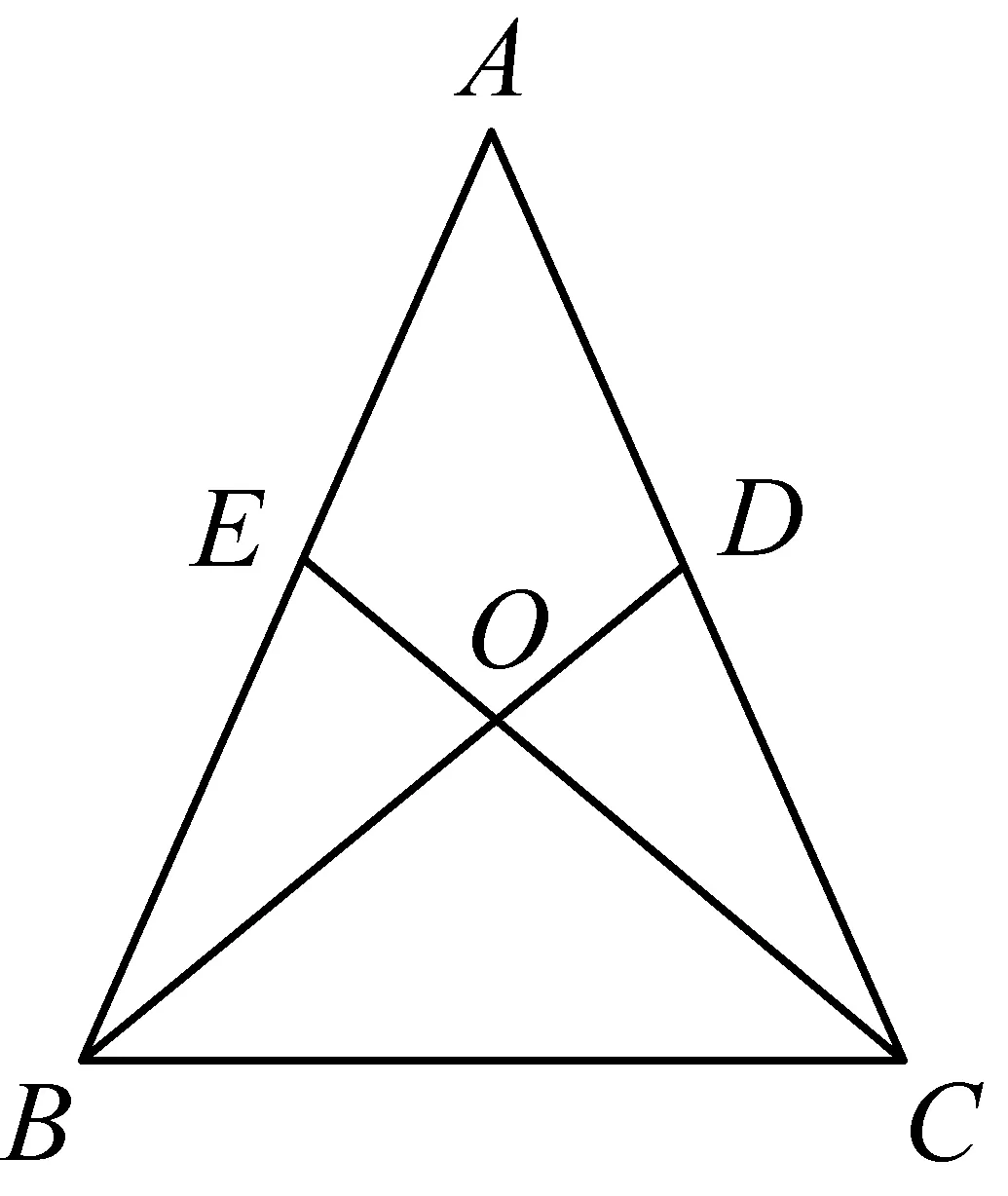
图9

(1)求证：△ABD≌△ACE；

(2)判断△BOC的形状，并说明理由．

本题考核等腰三角形的对称性，全等三角形的判定、性质，等腰三角形的判定；直观想象和逻辑推理，(1)属水平1；(2)属水平2.

例15如图10，在△ABC中，∠ACB=90°，将△ABC沿直线AB翻折得到△ABD，连接CD交AB于点M．E是线段CM上的点，连接BE．F是△BDE的外接圆与AD的另一个交点，连接EF，BF．

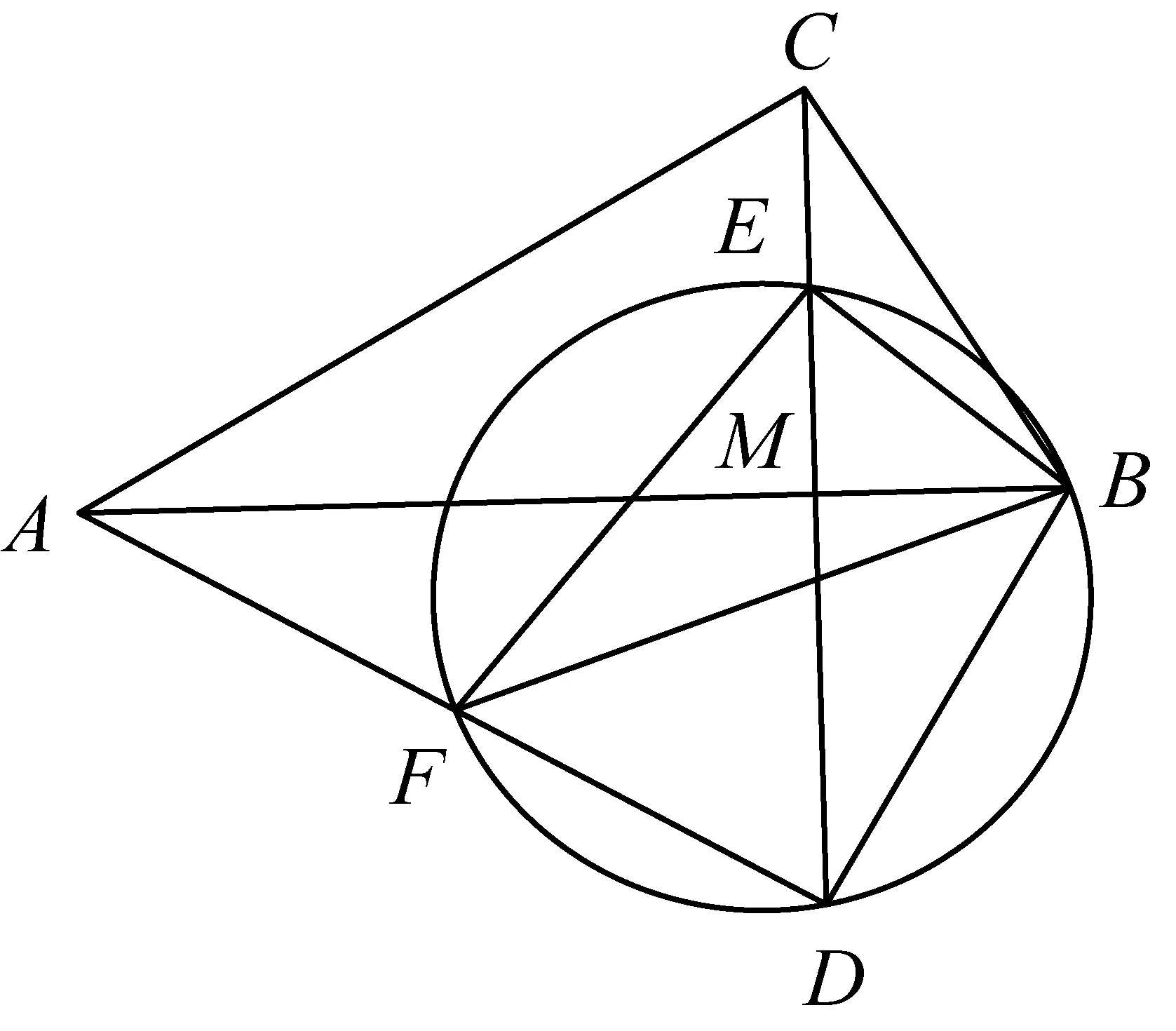
图10

(1)求证：△BEF是直角三角形；

(2)求证：△BEF∽△BCA；

(3)当AB=6，BC=m时，在线段CM上存在点E，使得EF和AB互相平分，求m的值.

本题以图形的轴对称和相似为背景，聚焦△BEF的形状以及其与△ABC的位置关系的逐步深入研究，考核轴对称、全等三角形、相似三角形、平行四边形、矩形、勾股定理等知识的综合运用，以几何问题研究为载体，综合考核直观想象和逻辑推理能力，属水平3.

3.3.3 统计与概率领域的命题——以数据分析为主线

统计与概率教学的课程目标总要求是：体验数据收集、处理、分析和推断的过程，理解抽样方法，体会样本估计总体过程；进一步认识随机现象，能计算一些简单事件的概率[19].与之相关的关键能力是数据分析.因此，以数据分析为主线，设计现实情境，考核样本估计总体思想、根据问题背景选择适当的数据分析方法分析数据的能力、用列举法求概率的方法、用频率估计概率方法，这是考核学生数据分析水平的基本策略.

例16在一次数学测试中，小明成绩72分，超过班级半数同学的成绩，分析得出这个结论所用的统计量是( ▲ ).

A．中位数 B．众数

C．平均数 D．方差

本题通过现实情境，考核学生在数据背景中理解统计量含义与特点，选择适当的统计量表述数据特征的能力，属水平2.

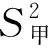
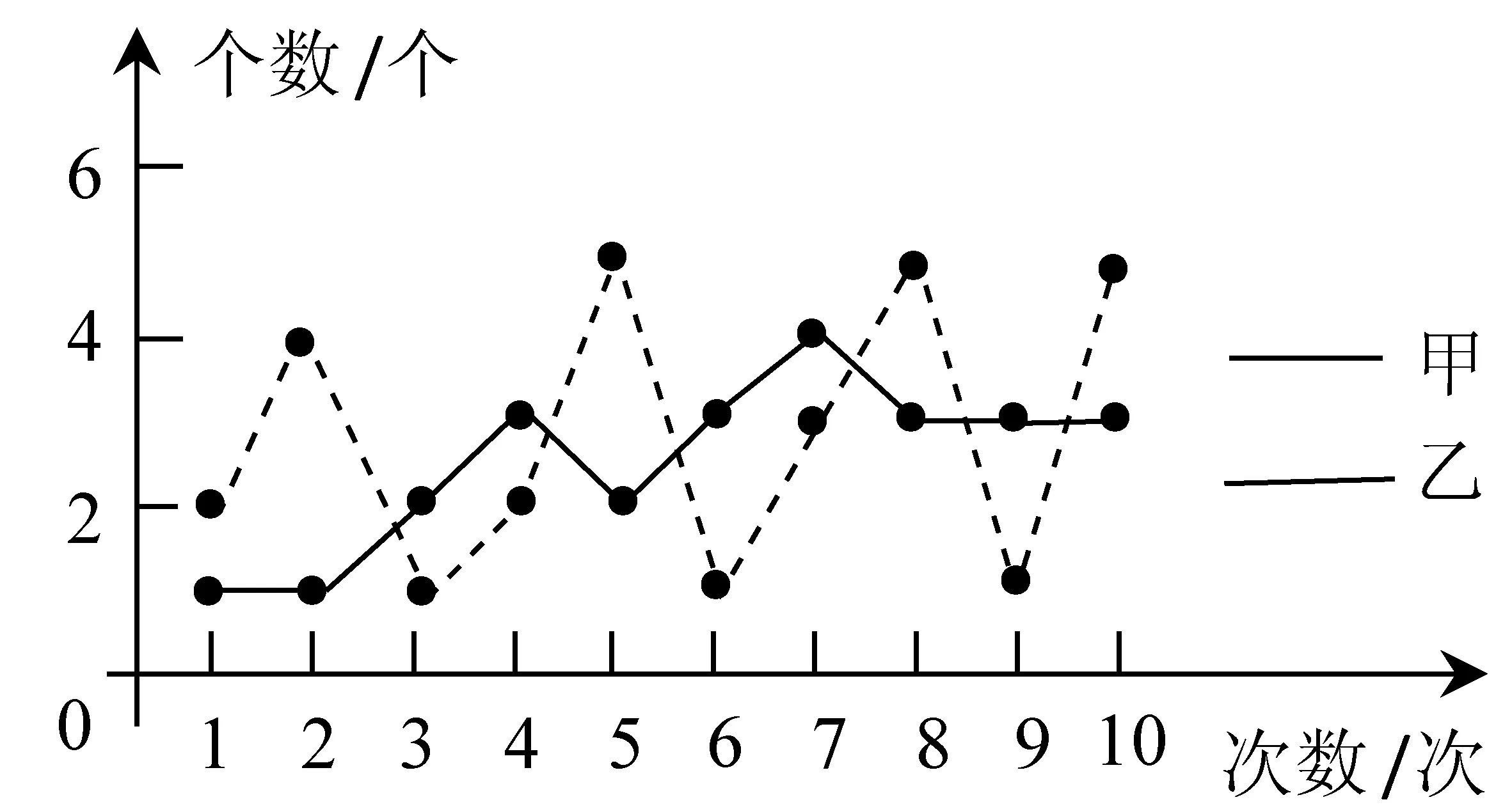
图11

本题考核对方差的波动意义的理解，属数据分析水平1.

例18新冠疫情期间，某校开展线上教学，有“录播”和“直播”两种教学方式供学生选择其中一种．为分析该校学生线上学习情况，在接受这两种教学方式的学生中各随机抽取40人调查学习参与度，数据整理结果如下表(数据分组包含左端值不包含右端值).

人数 参与度方式 0.2～0.40.4～0.60.6～0.80.8～1录播416128直播2101612

(1)你认为哪种教学方式学生的参与度更高？简要说明理由；

(2)从教学方式为“直播”的学生中任意抽取一位学生，估计该学生的参与度在0.8及以上的概率是多少？

(3)该校共有800名学生，选择“录播”和“直播”的人数之比为1∶3，估计参与度在0.4以下的共有多少人？

本题创设学生2020年经历过的在线学习情境，考核学生根据数据背景选择适当的数据分析方法分析数据的能力，考核对样本估计总体思想的理解，其(1)(3)属水平3，(2)属水平1.

3.4 基于实测数据的试卷质量分析

(1)难度.本卷的实测难度为0.746，其中数与代数领域实测难度为0.75，图形与几何领域实测难度为0.73，统计与概率领域实测难度为0.78，统计与概率试题稍简单，总体难度符合毕业考试的要求.

(2)区分度.用前30%学生的难度与后30%学生的难度差计算区分度，结果如下：整卷区分度0.47左右;选择题的整体区分度为0.3355，其中第5题的区分度在0.3～0.4之间，第8、9、10题的区分度在0.6～0.7之间；填空题的整体区分度为0.452，其中第14,16题的区分度均在0.4以上；解答题中，17、18题的区分度在0.3～0.4之间，21题、22题的区分度在0.4～0.6之间，19题、20题、23题、24题的区分度在0.6～0.8之间.试题的区分度比较合适.

(3)信度.用SPSS19.0分别对选择题(10个)，填空题(6个)，解答题(8个题目16个小题)共32个项目进行信度检验，结果如表2.

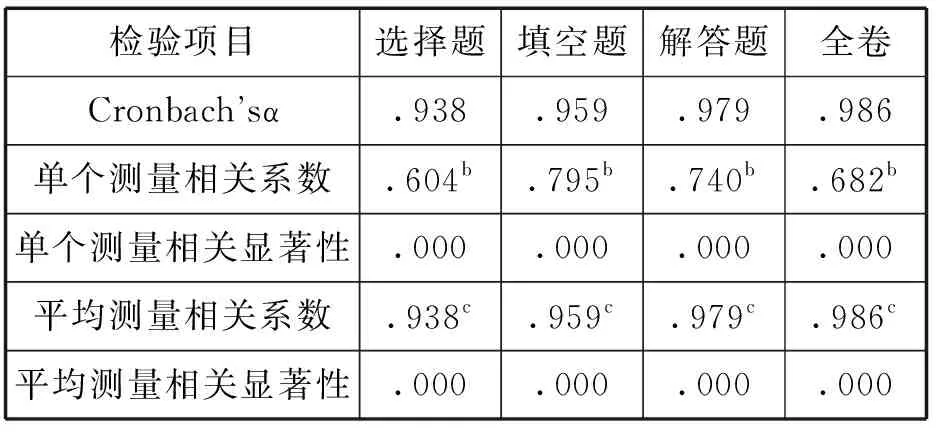
表2 试题信度检验

检验表明，试卷整卷和题目具有高信度.

(4)效度.用SPSS软件分析表明，本卷中所有题目与总分的相关系数均大于0.62，2～24题相关系数都在0.8以上(p<0.001),KMO 和 Bartlett检验结果如表3.

表3 KMO和Bartlett 的检验

说明整卷具有良好的效度，非常适合做因素分析.进一步，用SPSS因子分析方法分析关键能力不同水平，从中得到全卷的两个主成分：这两个主成分解析了总方差的86%多，如表4.

提取方法：主成分分析.

其中主成分1载荷大的对应着知识技能和较低水平关键能力(如表5)，主成分2载荷大的对应着高水平的关键能力(如表6).

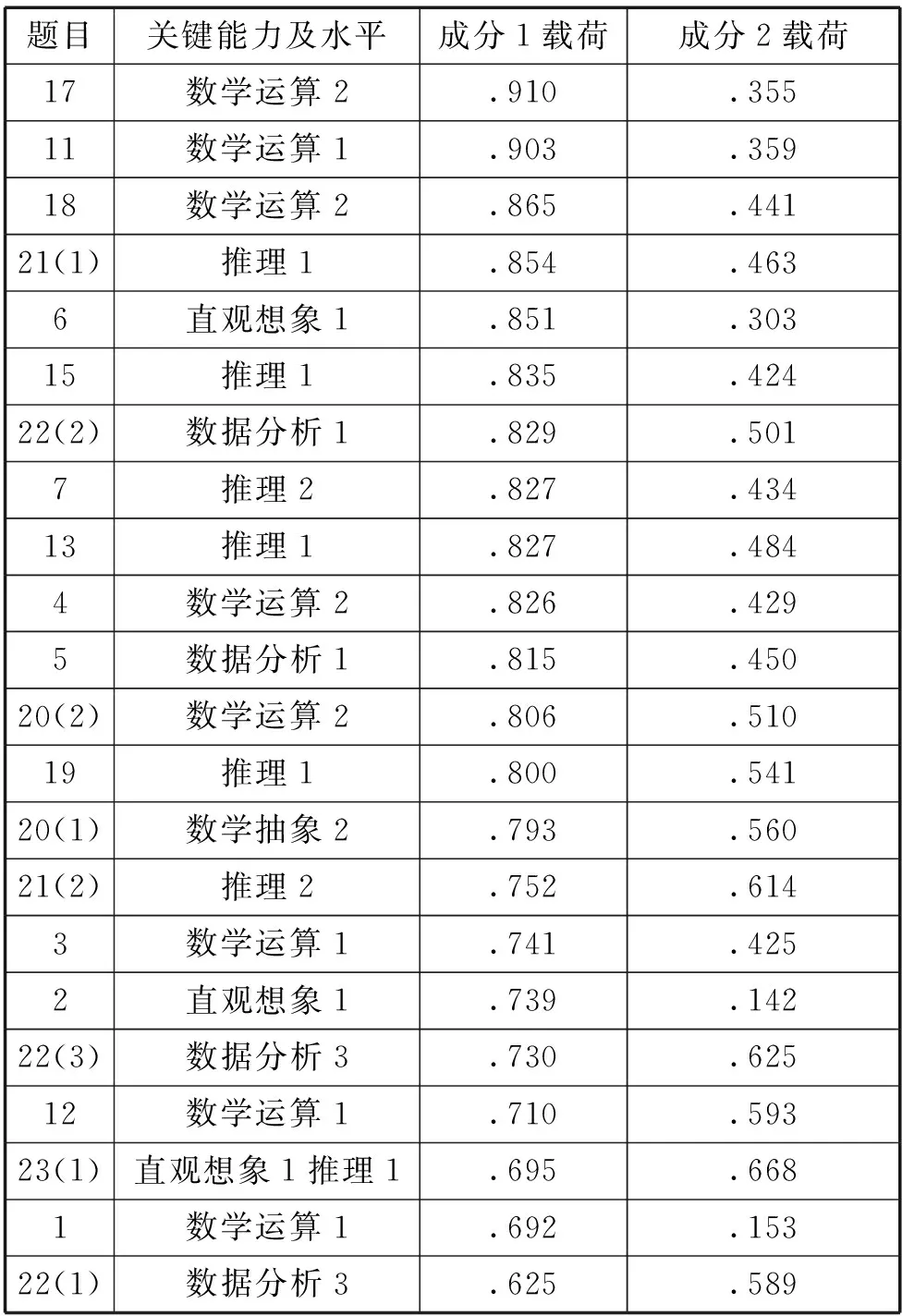
表5 成分1高相关变量及其载荷(相关系数>0.73)

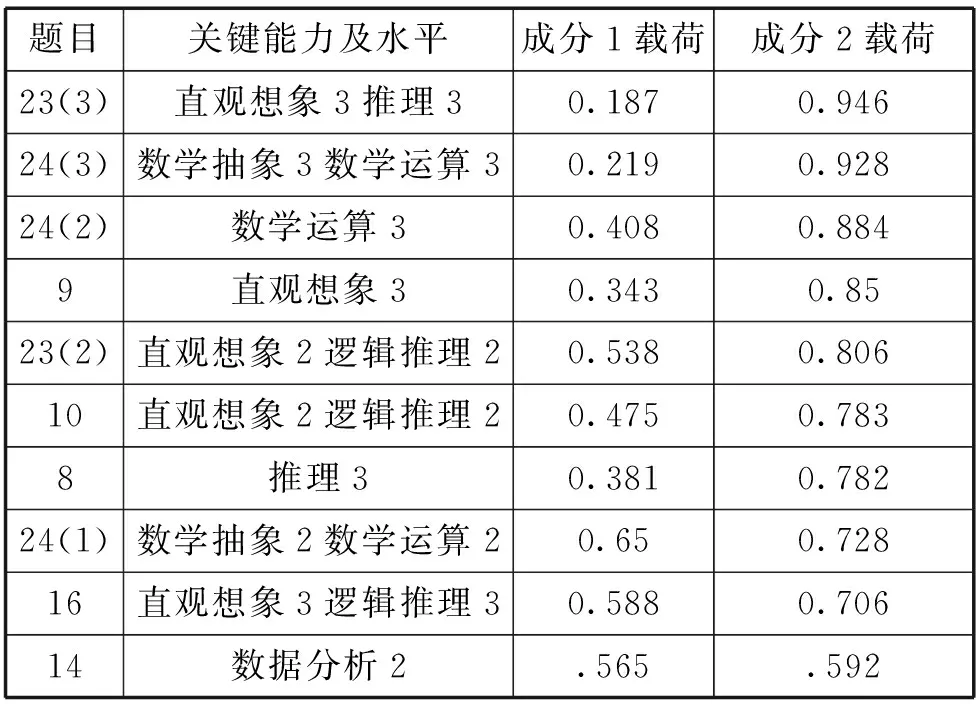
表6 成分2高相关变量及其载荷(相关系数>0.59)

以上分析表明，总体上试卷具有较好的测评学生知识技能和关键能力的效度,但试卷中统计综合题落在主成分1上，说明统计综合题的数据分析能力要求不够高，另外，双向细目表上分出了关键能力的三个水平，但数据分析表明只有两个层次.出现这种现象有两种可能的解释，一是试卷本身的关键能力的层次性不够明显，二是初中学生数学的关键能力还处于初级水平，主要区别在于有没有形成关键能力，而不是关键能力水平高低的差异,如果真是这样，那么，双向细目表上应该只在部分题目上列出关键能力，而且不需要划分关键能力的水平,当然，这需要更多的实证研究.

综上所述，前面命题实践中的试卷总体上难度适中、区分度合理、信度和效度较高，是一份有较高质量的试卷.

结束语随着数学课程改革进一步深化，考试命题面临重大变革.以教育部的《意见》为导引，研制数学学科综合素质导向下的学业水平标准，确定反映数学综合素质的关键能力，并在此基础上进行深入和广泛的实践研究,这对提高命题质量，正确导向立德树人的数学教学，进一步推进数学课程改革，具有重要的理论和实践意义.