数式同构 循脉生长①——人教版“整式的加减”章起始课教学设计

邢成云 刘晓玫

(1.山东省滨州市北镇中学实验初中部 256609 ；2.首都师范大学教师教育学院 100037)

“用教材教而不是教教材”早已成为我们的口头禅，但现实的践行并不乐观，固守教材的从教者不乏其人，这种“不敢越雷池一步”的教学情结仍然难以获解.尤其是对章起始课的教学关注不够，把它混同于一般的新授课，章起始课应有的先行组织者的作用发挥乏力，缺少对整章的统筹安排，使得节与节、课与课之间出现断裂，整体意识淡薄，不利于数学核心素养的落实.为此，笔者带领市名师工作室成员对章起始课进行探索，已初见成效，本文即开发的一个案例.

1 基于课标，整体规划

1.1 课标对“整式的加减”这部分内容的确定

1.借助现实情境了解代数式，进一步理解用字母表示数的意义；

2.能分析具体问题中的简单数量关系，并用代数式表示；

3.会求代数式的值：能根据特定的问题查阅资料，找到所需要的公式，并会代入具体的值进行计算；

4.理解整式的概念；掌握合并同类项和去括号法则，能进行简单的整式加法和减法运算.[1]

其中的1，2，3条是代数式的长程目标，贯穿于整个代数式学习的始终，需要在后续整式的乘除、分式、根式等学习过程中进一步发展落实，当下“整式的加减”一章将初步将其落实.

1.2 章引言、章头图的解读

章引言是全章起始的序曲，是全章内容的引导性材料，其主要教学功能体现在帮助学生了解本章学习的内容、地位和作用，唤醒并激励学生学习的兴趣和激情，培养学生应用数学知识解决问题的意识，有助于发展学生的核心素养.章引言教学应然要有“转轴拨弦三两声，未成曲调先有情”的效果.

本章的章引言以一个三小问的路程问题为主体，分别为整式的概念、合并同类项、去括号等的引入铺垫，整体揭示出本章学习的核心内容“整式的加减运算”；章头图是一张奔驰在青藏铁路上的列车的照片，是章引言问题的背景配图，配图上有一个线段图，以此可对章引言问题作出直观分析，另有与引言问题匹配的三个代数式，对它们的化简运算构成本章的研究主题.如此的图文并茂，对接了数学与现实生活，为数学抽象、构建数学模型提供了优质的素材(实际背景)，让学生感受到本章学习的必要性(实际的需要、数学的内需)，联手勾勒出了整章的学习脉络.

1.3 教材内容分析

教材分2大节：第一节整式；第二节整式的加减.本章是在学生学习了有理数、小学学过的用字母表示数和代数式等知识的基础上安排的.它属于《义务教育数学课程标准(2011年版)》(以下简称《标准》)中的“数与代数”部分，其主要内容包括整式、单项式、多项式；合并同类项；去括号；整式的加减运算等.这些内容既是对有理数的概括与抽象，它借力类比的思想方法，从数到式，从特殊到一般，彰显“数式通性”和式的一般性，体现数式之间的内在关联和数学内在的统一性，又是后继学习整式的乘除、分式和根式的运算、方程、函数等知识的基础，还是学习物理、化学等邻近学科及其他科学技术不可缺少的工具.

除了正文内容，还有3个活动，它们直接对接整式的应用，是通过现实情境历练学生思维的优质素材.

注重了数学应用意识的形成和培养，将教学目标的实现有机地融入到精心设计的情境中、过程中和应用中.体现了《标准》中的“课程目标”和价值追求.

就整式的加减的本质而言，就是对整式施行两种重要的恒等变形：一是合并同类项；二是去括号.整式的恒等变形是数学中符号运算的基础，是解方程的工具，在后继将要学习的代数知识几乎均与本章有关联.另外，本章也是培养和发展学生符号意识的重要素材.

基于课标的界定，通观现行的人教版教材，对本章作出如下整体规划：

第1课时：利用同构性，类比尝试形成本章的结构系统(充分利用章引言与章头图以及其它相关情境抽象出的模型，把本章的知识脉络揭示出来，形成研究路径，其中包括整式的概念、单项式、多项式及相关概念等具体知识).

第2课时：创设问题情境，把带括号的代数式嵌入，以此整体导入去括号、合并(同类项)等变形，揭示出本章的核心问题——整式的加减运算，加减运算的本质：去括号、合并同类项.

第3课时：分两个层级进一步熟悉整式的运算(一个层次是单项式、多项式的加减运算；第二层级是把化简与求值结合起来，打通与第一章之间的联系).

第4课时：活动课(教材P72的三个活动)，把数学模型、数学抽象等核心素养元素融入具有趣味性和探索性的挑战问题中，进一步熟练整式的加减运算，体会式优越于数的一般性.

第5课时：小结与复习(整体统摄复习课).

第1课时即为本节，是本章基于整体的起始课.若从“数与式”大系统视角来看，整式一章的起始课可以看成“数与式”领域的沿途起始课，它是(有理)数的生长、发展，具有数与式的同构性，可类比有理数递次展开，把“式”同化到“数”的结构中去.而如果把本章内容置于“式”的体系之中，本节课则属于代数式大单元“开山辟路”的“领域起始课”.本节课的“双重角色”体现出它的两个重要任务，一是类比数认识式；二是完成对式的整体架构，从而为以后所有“式”的教学开山问路，埋下伏笔.

2 基于同构，整体授受

2.1 教学目标

1.回顾有理数的章结构图式，类比构筑(代数)式的整体结构图式，初步感知“数式通性”；

2.在具体的情境中能分析其中的数量关系，列出一些代数式，通过字母表示数，理解字母表示数的意义，体会具体和抽象的内在联系和数式的内在统一性；

3.在列式的基础上，通过分类了解有理式、整式、分式、单项式、多项式及相关概念，以及它们之间的区别与联系，感知分类意识.

2.2 教学重难点

1.类比建构式的整体结构图式和整式、单项式、多项式的概念及联系的认识是重点；

2.对列出式子的分类是教学的难点.

2.3 教学过程设计

2.3.1 从数到式，初成图式

问题1：我们刚刚完成了第一章“有理数”这一百花园的游览，大家都收获满满，请同学们回顾一下，欣赏了哪些景点？是按照怎样的脉线进行的？请同学们把自己课前梳理的结构展示出来，小组代表展示.

预设：通过小组代表交流，达成共识，形成有理数一章的结构.

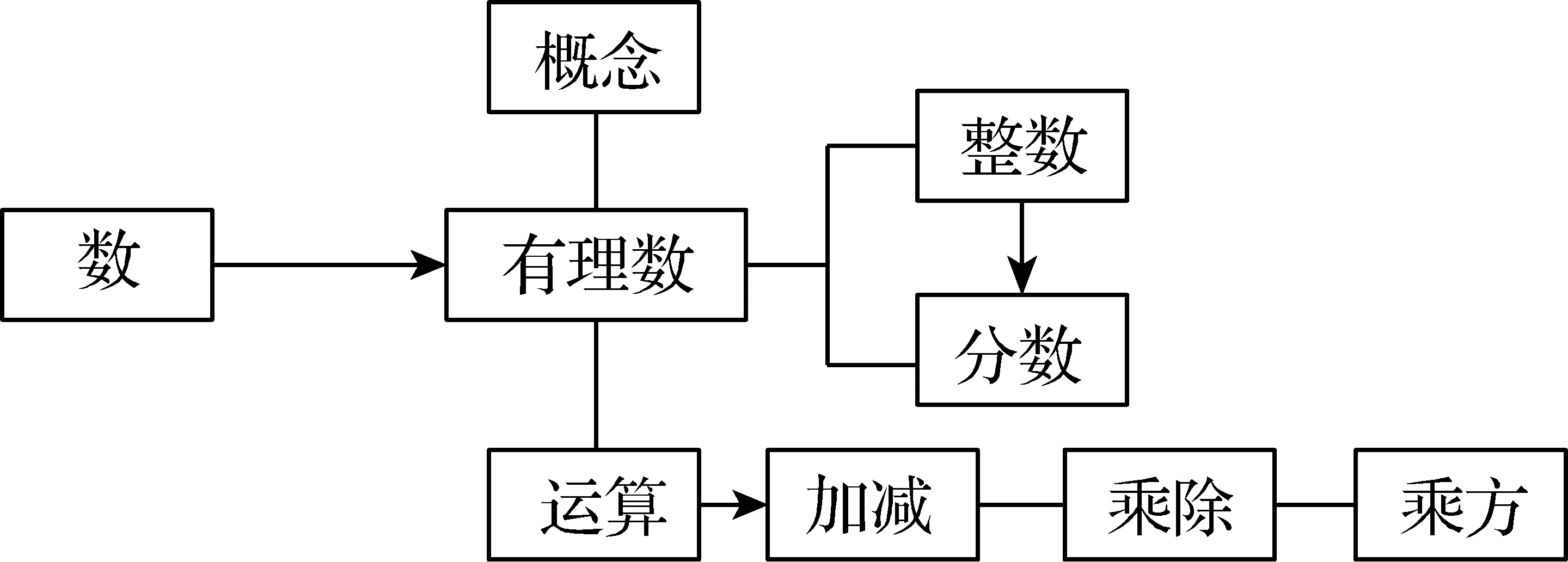
问题2：其中的运算离不开运算律，那有理数的运算律有哪些？

加法的交换律、结合律，乘法的交换律、结合律以及分配律，分别对应着

a+b=b+a，(a+b)+c=a+(b+c)，

ab=ba，(ab)c=a(bc)，a(b+c)=ac+bc.

经过教研室讨论，设定教学要求1～5的权重值和实验教学环节分值，直接计算出各个指标点相应的评价分数，具体如表1所示。按照工程教学认证中课程与毕业要求达成度的计算方法，得到最终的课程质量评价的量化指标(K)，如公式1所示。如果K值大于0.7，则认为学生达到了课程的基本要求。

追问：为什么用字母来表示运算律？比如用2+3=3+2表示交换律不可以吗？

预设：不可以.

追问：为什么？

因为2和3只是两个具体的数，不具有一般性，而a、b是字母，具有一般性的特点.

追问：请大家观察这两个式子所表示的意义有什么不同？

预设：第二个式子是第一个式子的特殊情况.

再看一个例子：

小刚今年7岁，小强5岁，如果小刚9岁了，那么小强几岁？到小刚18岁时，小强多少岁？由此可以发现只要知道小刚的年龄，就可以知道小强的年龄，那这二人的年龄有怎样的关系？

追问：如果让同学们用小刚的年龄去表示小强的年龄，该怎么办？

预设：遇到阻力，估计有的学生会说，小刚的不知道多大，怎么知道小强的，此时可追问，当不知道的时候，我们以前怎么做过？

生：假设是多少.

师：对，我们可以作假设，一般作假设用什么表示？

预设：用1、x等.

师：对本题而言，用什么更合适.

预设：字母x，1是具体的，在假设工程问题的整体工作量时一般用“1”.

师：说得好，那若用字母x表示小刚的岁数，那么小强的岁数该如何表示?

预设：x-2.

设计意图为了让类比更有力量，课前安排了对有理数结构的梳理，一开课通过小组交流，成共识而沉淀下来备用，培根固原，才会有更好地生长；然后通过数学本身以及生活中常见的例子，激活或唤醒学生思维，从两个角度让学生感知数的局限性和字母出场的必要性、体会用字母表示数的一般性，使学生理解认识事物的过程是由特殊(具体)到一般(抽象)，又由一般(抽象)到特殊(具体)，在不断往复中得到提高，培养学生初步的辨证唯物主义观点.通过数与式之间的联系，体现数学知识间具体与抽象的内在联系和数学的内部一致性.

师：我们发现用字母表示数更具有一般性.从这章开始，我们将进入一个崭新的式子的世界. (教师板书：式，并用“字母表示数”连缀(在结构图上纵写，如下框图))

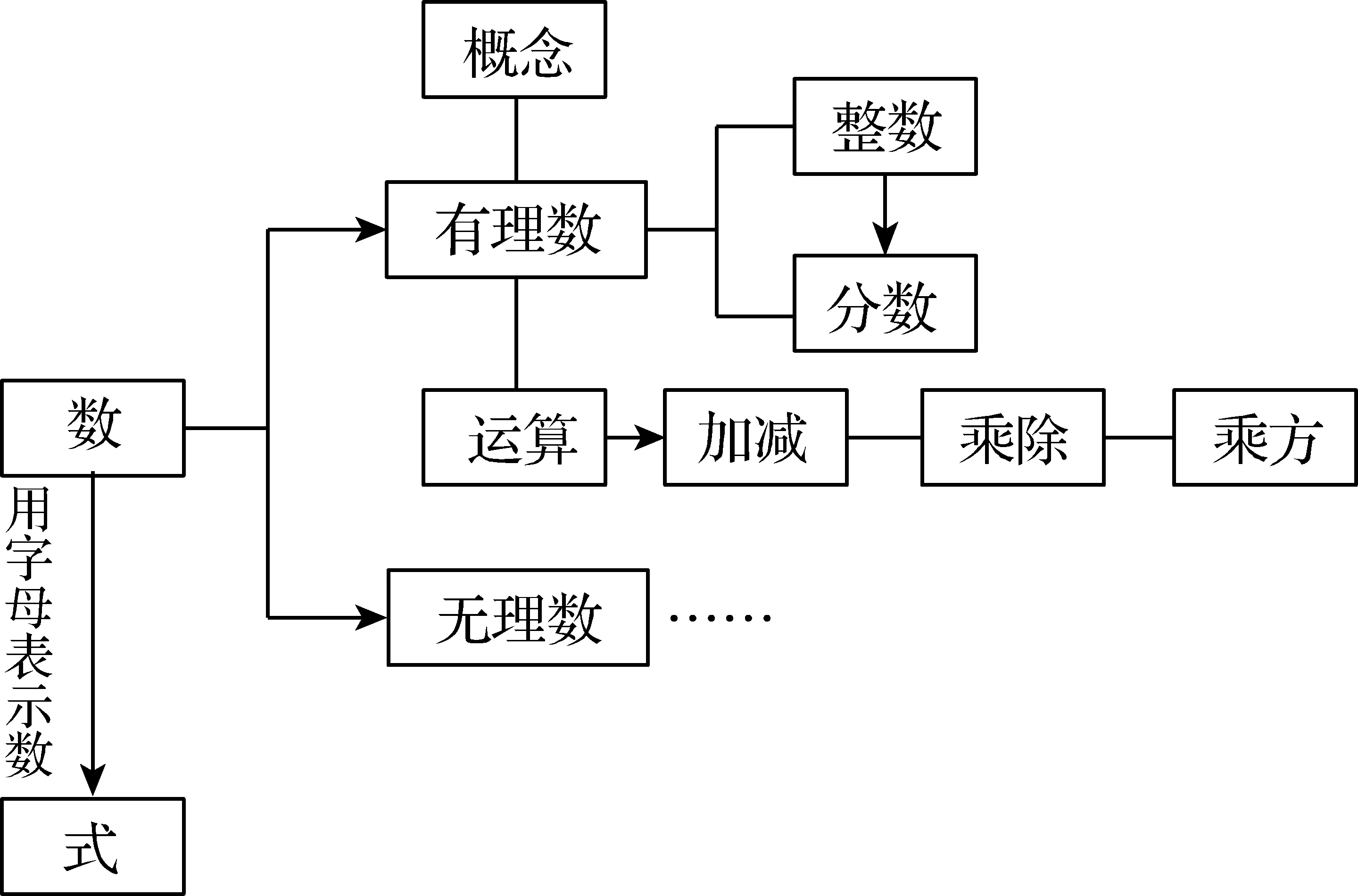
师：既然字母可以表示数，说明它们具有相通性，那根据“有理数”的学习内容及思路，请同学们大胆猜测、构想一下“式”的学习内容及思路怎样？

预设框图：

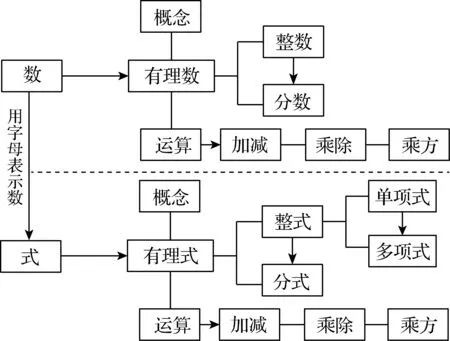
设计意图基于数与式的同构性，引导学生大胆构想，勾勒出有理式的整体结构，从相克相生的视角来看，有理式的架构就是有理数的自然生长，随着学习的深入，不断地伸展枝杈，直至成长为枝繁叶茂的数式系统大树.如此，让教学变成生长系统.其中，整数到分数的箭头体现它们的对立统一性，即整数相除得分数，单项式的加减产生多项式，整式到分式的箭头是类比产生的.

2.3.2 字母代数，语句(文字)成式

师：请同学们尝试列式表达以下的数量关系：

问题3：(1)香蕉原价是每千克m元，半价出售，现价是多少？

(2)一个长方体包装盒的长和宽都是acm，高bcm，用式子表示它的体积；

(3)n的立方的相反数如何表示？

(4)七年级四班有学生n人，其中男生有m人，那么女生的人数？

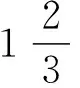
(6)育才中学原有a台电脑，暑假新购进b台电脑，同时淘汰c台旧电脑，该中学现有电脑的台数?

(7)李子每千克x元，橘子每千克y元，香梨每千克z元，买2千克李子，5千克橘子，1千克香梨需要的钱数？

(8)如图1，某建筑物的窗户，上半部为半圆形，下半部为矩形，如图所示.已知矩形的长、宽分别为a、b，这扇窗户的透光面积是________.

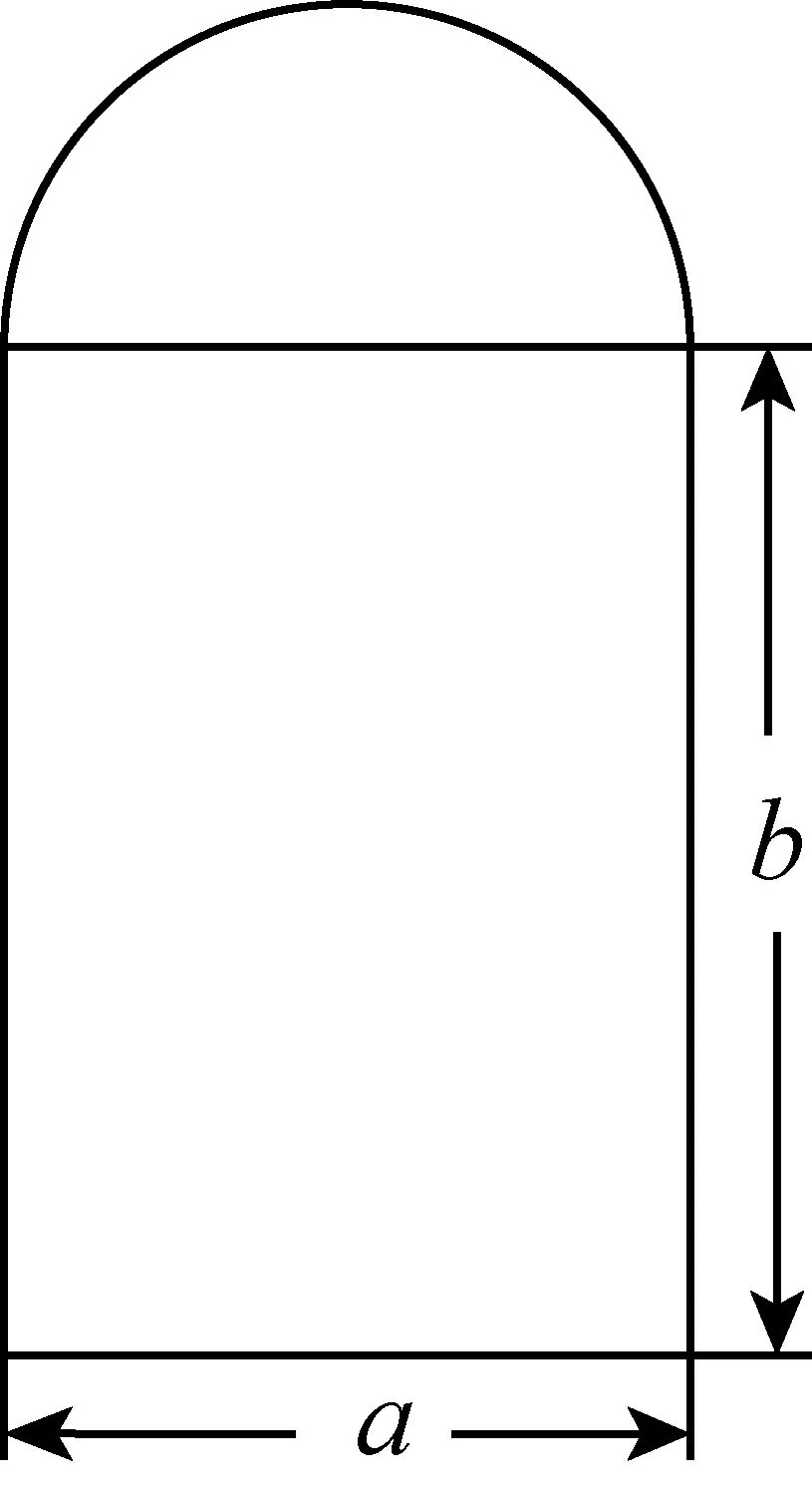
图1

(9)图2是一所住宅的建筑平面图(图中长度单位：m)，用式子表示这所住宅的建筑面积________.

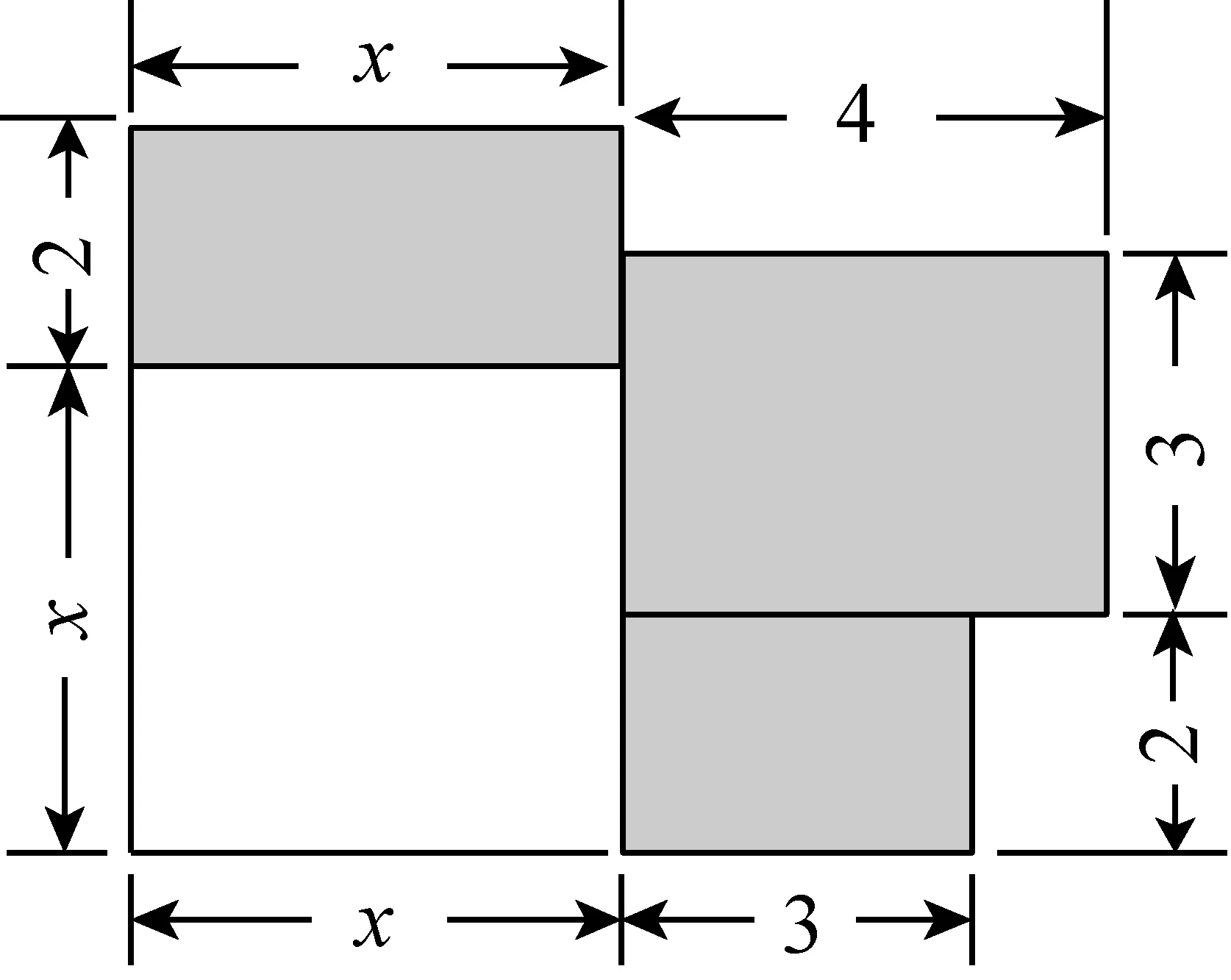
图2

(10)从小敏家到学校的路程是3千米，小敏骑电动车的速度是a千米/时，小敏骑电动车从家到学校需要的时间？

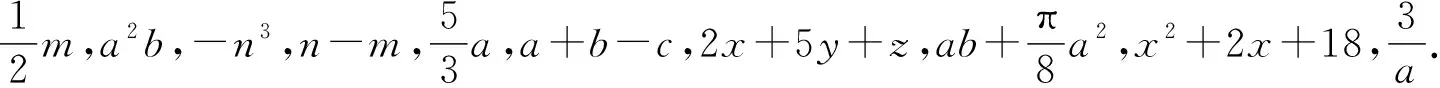
问题1结束之后，提出问题：回看我们解决以上问题的过程，同学们认为在列式表示数量关系时，书写应该注意什么？

生回答，教师根据学生回答情况进行总结.

设计意图由实际问题或数学问题的文字语言转译成符号语言，这本身就是数学的抽象.给出10个小问题情境，在获得10个代数式，为下一环节的分类有意识地提供素材的同时，唤醒学生小学对它的一些粗浅认识，并顺势指导学生书写代数式的规范性和注意事项：第1个问题，规范数与字母相乘时用“·”或省略乘号的格式；第2个问题，规范有多个相同因数相乘时，写成乘方的形式；第3个问题，规范当1或-1与字母相乘时，其中的因数1省略不写；第5个问题，规范当带分数与字母相乘时，带分数必须化成假分数；第6、7、8三个问题，规范和差结果的代数式若有单位，要加括号括起代数式等.同时，让学生体会字母与数一样，同样可以参与运算.

以此渗透同一个式子可以表示不同的含义，从而反衬字母表示数的一般性.

学生在小学已经学习过含字母式子的书写，设置类似问题既有唤醒之意，又有深化之引，当然在此设置更关键的是以此作素材的进一步学习.

2.3.3 尝试分类，同构生长

单项式的概念在整式的学习中起着至关重要的作用，为了引导学生进行学习，创设下面的问题情境：

要求：同学们先独立思考，完成以后再小组交流.

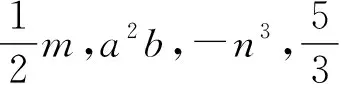
追问1：第二类的5个式子又有什么共同特征呢？起个什么名字合适呢？

预设：由于是几个单项式的和、差，即含有多个单项式，故名多项式.

追问2：那个另类的式子，怎样命名合适？

预设：最后一个外观上像分数，而又不是分数，是一个式子，故名分式(学生未必获得).

有了分式的出现，至此，就可以告诉学生，单项式、多项式统称为整式.让开始同构猜想的架构落到了实处(骨架上长出了血肉).

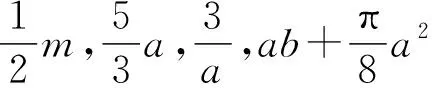
解剖整式——根据定义，单项式中的数字因数叫单项式的系数，字母因数的个数叫单项式的次数；多项式有几个单项式组成就叫几项式，取其中每个单项式次数的最高次确定为多项式的次数，不含字母的项叫常数项.在此返扣四个单项式熟悉单项式的系数与次数概念；用“x2+2x+18”熟悉多项式的有关概念.

2.3.4 梯度进阶，再度生长

问题5：青藏铁路线上，在格尔木到拉萨之间有一段很长的冻土地段，列车在冻土地段、非冻土地段的行驶速度分别是100 km/h和120 km/h.请根据这些数据回答下列问题：

(1)列车在冻土地段行驶时，2 h行驶的路程是多少？3 h呢？th呢？

(2)在西宁到拉萨路段，列车通过非冻土地段所需时间是通过冻土地段所需时间的2.1倍，如果通过冻土地段需要th，能用含t的式子表示这段铁路的全长吗?

(3)在格尔木到拉萨路段，列车通过冻土地段比通过非冻土地段多用0.5 h，如果通过冻土地段需要uh，则这段铁路的全长可以怎样表示?冻土地段与非冻土地段相差多少千米?

预设：(1)200，300，100t；

(2)100t+120×2.1t；

(3)100u+120(u-0.5)，

100u-120(u-0.5).

思考1：面对(2)中的多项式100t+120×2.1t，同学们有没有化简的想法？怎样化简？

由此，引出同类项、合并同类项.

思考2：(3)中的两个式子与前面所列的式子又有什么不同?

预设：与(2)相比多了括号，要能和“100t+120×2.1t”一样进行化简应该需要去括号，由此导引出去括号的变形，至此，本章的核心知识——“整式运算的本质”就现形了.

问题6：笔记本的单价是x元，中性笔的单价是y元，小红买了3本笔记本，2支中性笔；小亮买了4本笔记本，3支中性笔.用式子表示她们一共花了多少钱？(要求：用两种不同思路)

预设方法一：两人各自花钱的和(3x+2y)+(4x+3y)；

预设方法二：整体看作笔记本钱和中性笔钱数的和(3x+4x)+(2y+3y),借助生活经验即得7x+5y.

教学说明若只出现一种方法，可进行引导，让两种思路尽现，以备比较之用.形式不同，结果应该一样，即(3x+2y)+(4x+3y)应该等于7x+5y，这就隐含着一个问题：去掉括号，再化简，以此呼应一下问题5，共同把去括号、合并同类项揭示出来，再次指向整式的运算本质.

师：根据前面刚刚获得的单项式、多项式及相关概念的认识，依次回答问题5、问题6中出现的300，100t；7x+5y分别属于哪一类式？是单项式的追问系数、次数，是多项式的追问项数、次数.

过程略.

设计意图回归章前语中的问题，及问题6(教材68页中的例7)，通过列式再次感知用字母表示数，让学生体会式子可以简明的表示实际问题中的数量关系，它比只有具体数字表示的算式更有一般性，通过辨识式的类型和追问进一步巩固有理式的相关概念.式子中的字母表示数，同数的地位一样，所以式子同样可以进行运算，数的运算是式子运算的特殊情形，这样问题5与6的联手共同烘托出了去括号以及同一类型合并的变形，为本章后继加减运算交了底，至此，一章的学习脉络就清晰了，结构愈加丰满了.

2.3.5 返扣结构，明确主旨

问题7：同学们，我们一起回顾一下这节课是怎样学习的？

预设：类比数的学习思路展开的学习.

问题8：在学习单项式、多项式等概念时，我们是如何进行的？

根据实际问题列式(抽象)，然后对式分类获得的.

师：同学们说得很好，我们不但构想出了式的学习脉络，获得了本章要学习的核心知识及内在联系(重色在结构图中呈现或用多媒体技术闪烁本章要学习的部分)，还尝试使用了数学上的类比、分类、抽象、一般与特殊等思想方法，值得庆贺.

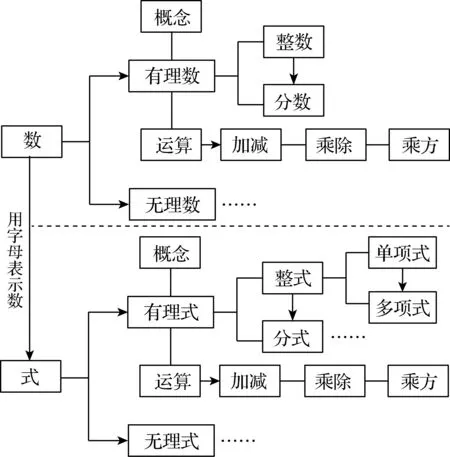
设计意图旨在让学生总结这节课所表达的数学思想并“显化”，并且让学生清晰“代数式”这一章基本框架和学习要求，类比学习数的基本经验，避免学习的盲目性，增强学生学习的主动性，使学生对学习进程心中有数，从而学会学习、学会研究，最终达到数学育人的目的.

3 反思评价

3.1 基于同构，类比贯通

奥苏贝尔根据新、旧知识的上、下位关系将学生的新知识学习分为上位学习、下位学习和并列结合学习.本节课整式的学习就是基于“有理数”的上位学习，是从数到式的关联，并且这种关联性是同构的，故在梳理有理数学习的基础上，基于小学就会的“用字母表示数”，利用数与式的同构性“类比”展开对这一章的学习.当然，本节的学习是在其上的提升与发展.类比这种“策略性知识”知识的应用在本节课共有三处：第一处是借助有理数的学习内容得出整式的学习内容；第二处是借助有理数定义得出有理式的定义；第三处是借助数的产生过程得出式的产生过程，这其中也蕴含了由有理数的运算得出单项式的运算，单项式的加减运算产生多项式，单项式(多项式)的除法运算可产生分式等.这些学习经验的积累都是以后学习中的“精髓”，如果学生领悟了这些数学的“真谛”，后继的学习就会变得顺乎其然.

3.2 重组教材，循脉生长

在初中学段“数与代数”领域中，数及其运算、字母(式)及其运算都是数学的核心内容.整体来看，这可以看成一个大单元，当然，也可以分开来看成两个中单元，它们自始至终贯穿于整个初中的数学课程.基于此，本节课整体立意，进行知识重组.本来，单项式与多项式在教材中是两块独立的教学内容片断，但它们之间有着紧密的关系.在对它们进行整体化的教学处理中，获取整式的知识架构，这有利于学生对单项式与多项式对立统一的理解和相关概念的识别.这样，作为章起始课在落实“四基”教学目标的同时，也关注了本章知识体系的建构，感受单项式、多项式等章的概念和合并同类项的方法等，对本章内容有一个大致的了解，让学生对学习进程心中有数，帮助学生建立有意义学习的心向，为接下来这一章“精致”的学习埋下一颗种子，最后达到让学生感受到“数与式”运算一致性的目的.这种整体建构的教学，不仅使学生获得了数学知识，还积累了数学基本活动经验，使得整个教学过程彰显出以“运算方法”为纽带的生长态势，如此一来，还为后程“分式”(除法)和“根式”(开方)的学习做了铺垫，埋下伏笔，从而建立代数式整体观念的一贯性，荷起章起始课开山问路、高远立意的责任担当.