第十届中学数学水平能力测试(高三M-A)试卷

编者按：《中学数学水平能力测试》以“自己与自己比”为理念，激发学生的数学兴趣，为广大学子提供一个锻炼和检验自己的平台.M-A试卷考察的知识范围为整个中学数学，这个测试源于2014年北京数学会开始主办的中学数学水平能力测试.

一、选择题：本题共8小题，每小题5分，共40分.在每小题给出的四个选项中，只有一项是符合题目要求的.

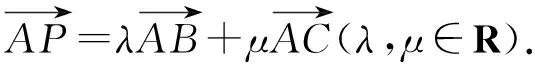
(A)直线BC上任一点P都有λ+μ=1成立．

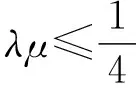
(C)直线BC上存在点P，使得λ<0且μ<0．

(D)满足λμ<0的点P，都不在线段BC上．

答案：C

(供题人：北京海淀进修学校附属实验学校 郝俊奎)

2．在三角形ABC中，CA=3,CB=5，角平分线CE交AB边于点E，则线段CE的取值范围是

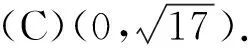
答案：D

(供题人：北京工业大学附中 肖志军)

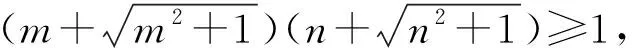
(A)m+n≥0． (B)m+n≤0．

(C)m-n≥0． (D)m-n≤0．

答案：A

(供题人：北京牛栏山一中 李金彪)

4．一只虫子白天移动晚上休息．在第一天白天，它从点O出发，向东移动了5个单位长度．每天晚上虫子会逆时针旋转60°．每天白天虫子会沿新的方向移动，且移动的距离是前一天的一半．最终虫子无限接近点P．那么OP2=

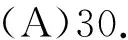
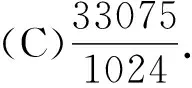
答案：B

(供题人：北京海淀进修学校附属实验学校 任泽乾)

5．设A是非空实数集，若对于∀x,y∈A，都有x+y,x-y,xy∈A，则称集合A具有性质P. 给出以下命题：

(1)若集合A具有性质P，则A在整数集Z中的补集具有性质P．

(2)若集合A1,A2具有性质P，则A1∪A2具有性质P．

(3)若集合A1,A2具有性质P，则A1∩A2具有性质P．

其中真命题的个数是

(A)0． (B)1．

(C)2． (D)3．

答案：B

(供题人：北京汇文中学 田会永)

6．在平面上给定圆O与定点A，设点B是圆O上的一个动点，线段AB的垂直平分线CD与直线OB相交于点E，则点E的轨迹不可能为

(A)圆． (B)椭圆．

(C)双曲线． (D)抛物线．

答案：D

(供题人：北京昌平一中 刘克光)

7．对于集合S，用|S|表示集合S中的元素个数，用n(S)表示集合S的子集个数. 已知A,B,C是三个有限集，且|A|=|B|=2020，n(A)+n(B)+n(C)=n(A∪B∪C)，则|A∩B∩C|的最大值是

(A)2017． (B)2018．

(C)2019． (D)2020．

答案：C

(供题人：北京十一学校 潘国双)

8．在直角坐标平面内，定义A(x1,y1),B(x2,y2)两点间的“直角距离”为

d(A,B)=|x1-x2|+|y1-y2|.

在这个定义下，给出以下三个结论：

(1)在三角形ABC中，若∠C=90°，则[d(A,C)]2+[d(C,B)]2=[d(A,B)]2．

(2)到坐标原点的“直角距离”等于1的点的轨迹是正方形．

(3)到M(-1,0),N(1,0)两点的“直角距离”之和为4的点的轨迹是六边形．

其中正确结论的个数是

(A)0． (B)1．

(C)2． (D)3．

答案：C

(供题人：北京昌平一中 刘克光)

二、填空题：本题共8小题，每小题5分，共40分.

1.集合{(x,y)|x2+y2≤|xy|+9,x∈Z,y∈Z}中元素的个数为________．

答案：49

(供题人：清华大学附属中学 郎春雨)

2．设15100是n位数，则n=________． (参考数据：lg2=0.3010,lg3=0.4771)

答案：118

(供题人：北京陈经纶中学 孙丕训)

3．已知集合I={1,2,3,4,5,6},A={(s,t)|s∈I,t∈I}．若B⊆A，且对任意的(a,b)∈B，(x,y)∈B，均有(a-x)(b-y)<0，则集合B中元素个数的最大值为________．

答案：6

(供题人：北京昌平二中 刘晶)

4．设(x2-x+1)1010=a0+a1x+a2x2+…+a2020x2020，则a0+2a1+3a2+…+2021a2020=________．

答案：1011

(供题人：北京工业大学附中 肖志军)

5．已知函数f(x)=x2-6x+a(ex-3+e-x+3)有唯一零点，则a=________．

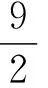
(供题人：中国人民大学附属中学 王鼎)

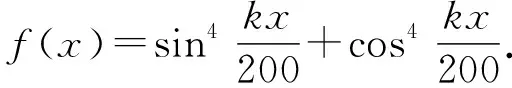
答案：315

(供题人：北京工业大学附中 肖志军)

7．已知数列{an},{bn}满足：a1=2，b1=1，an+1=3an+bn，bn+1=an+3bn．使得an>2020的最小正整数n为________．

答案：7

(供题人：清华大学附属中学 郎春雨)

8．单位圆的内接正五边形的一个顶点到另外四个顶点距离的乘积为________．

答案：5

(供题人：审题组)

三、双填空题：本题共4小题，每小题两空，每空5分，每小题10分，共40分.

1．已知a,b,c满足a+b+c=1，a2+b2+c2=5，abc=0，则ab+bc+ca=________，a3+b3+c3=________．

答案：-2，7

(供题人：北京十一学校 潘国双)

2．已知实数x,y满足x2-xy+4y2=4．记x2+xy+4y2的最大值为M，最小值为m，则M=________，m=________．

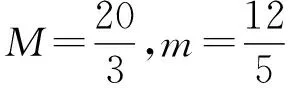
(供题人：北京四中 贾祥雪)

3．函数f(x)=sin3x+cos2x+2|sinx|的最小值为________，最大值为________．

答案：0, 2

(供题人：清华大学附属中学 郎春雨)

4．将30写成若干个相同的整数相加，则这些整数相乘最大为________；将30写成若干个相同的数相加，则这些数相乘最大为________．

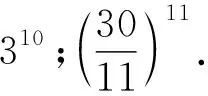
(供题人：中国人民大学附属中学 王鼎)