利用GeoGebra软件进行可视化探究教学——以2020年高考数学北京卷20题为例*

翟洪亮 (江苏省太湖高级中学 214125)

商再金 (江苏省灌云县教师发展中心 222000)

高中数学教学以发展学生数学学科核心素养为导向，因此需重视利用信息技术创设可视化的教学情境，启发学生思考，引导学生把握数学内容的本质，通过信息技术与教学内容的深度融合，提高教学的实效性．GeoGebra动态数学软件(下称GGB)是由美国数学教授Markus Hohenwarter在2002年创建的一款将几何、代数、表格、图形、统计和微积分集中在一起的容易使用的软件，它以可视化的直观方式赢得了数学教师的青睐．

高考试题由专家组精心命制而成，有些试题看似平常实质超常，往往蕴含着漂亮的性质，有较大的研究空间和教学价值，值得我们去探究．圆锥曲线中的定点、定值问题是高考的热点．本文对2020年全国高考数学北京卷20题进行探究，猜想其蕴涵的性质，先通过GGB软件进行验证，然后给出证明，并将它们推广到其他圆锥曲线.现整理成文，供同行参考．

1 试题

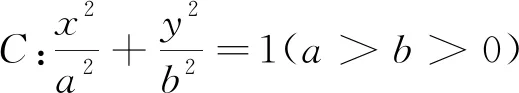
(1)求椭圆C的方程；

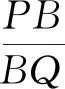
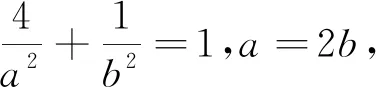
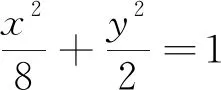
2 探究

本题考查直线方程、直线与椭圆的位置关系，试题运算量较大，区分度明显，注重对数学运算素养的考查．做完此题后，笔者利用GGB软件的可视性进行如下探究：

问题1若连结AB，则直线AM,AN,AB的斜率之间有何关系？

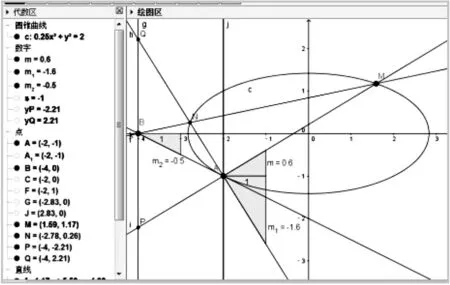
图1

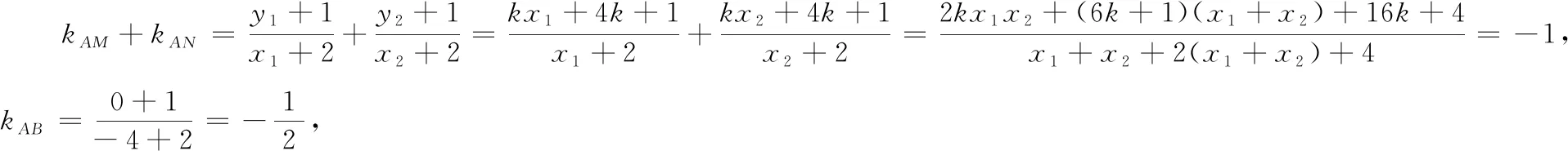
问题2命题人为何要取椭圆上的点A(-2,-1)？如果选取其他点，那么BP=BQ，kAM+kAN=2kAB还成立吗？

利用GGB软件可以发现，当且仅当点A位于(-2,-1)和(-2,1)两处时，有(1)kAM+kAN=2kAB；(2)BP=BQ．由(-2,-1)和(-2,1)两点联想到：

问题3当点A是直线x=-2上的动点时，上述两个性质还成立吗？

利用GGB软件，发现上述两个性质仍然成立．

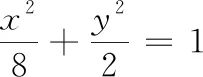
发现点A的横坐标以及直线x=-4与x轴交点的横坐标之间的关系为(-2)×(-4)=8，即xAxB=a2．由此特殊情形可猜想到一般情形：

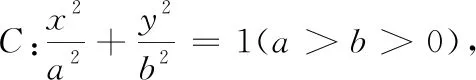
这个猜想正确吗？不妨先利用GGB软件来验证一下：

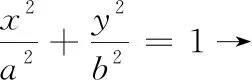
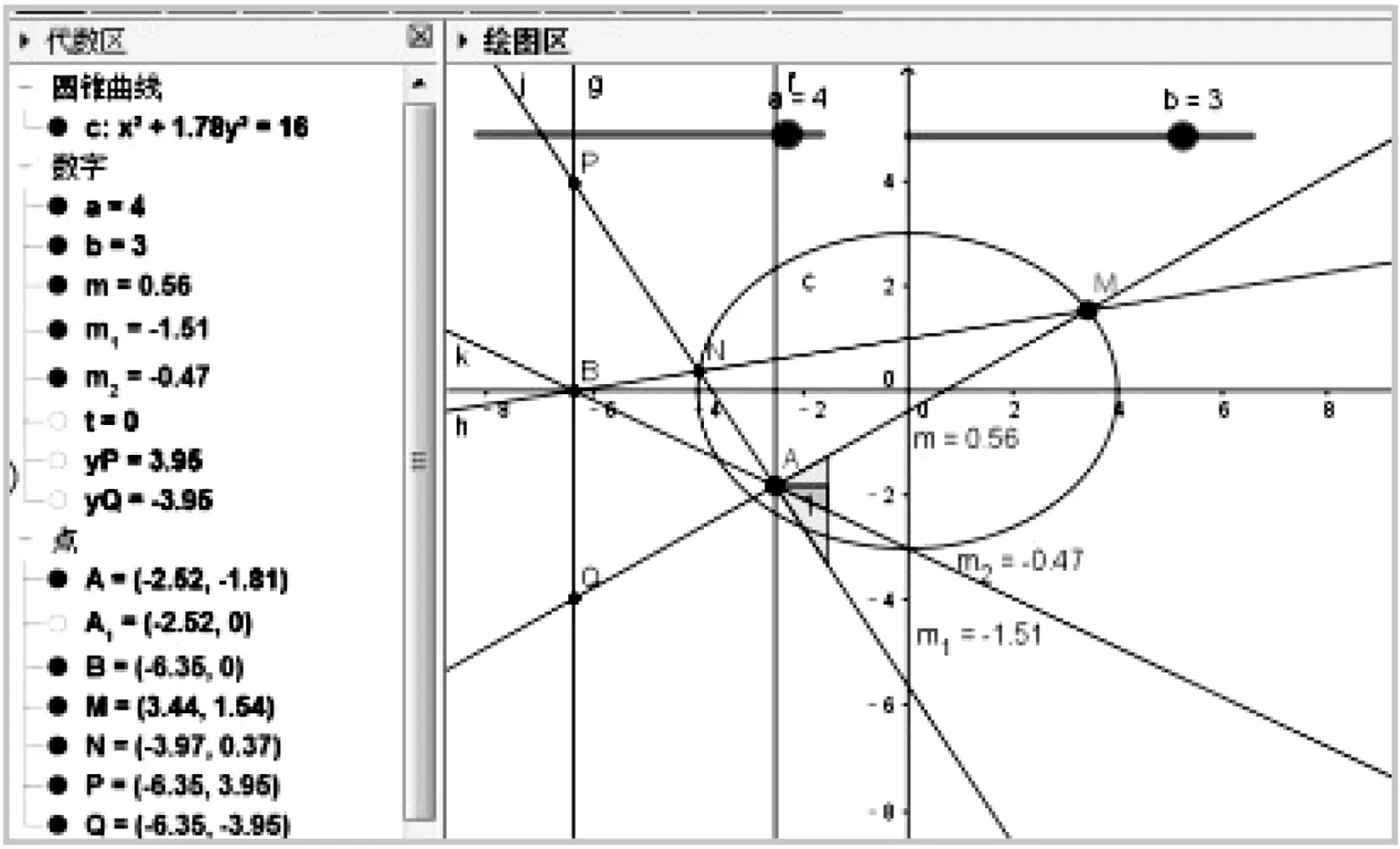
图2

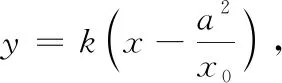
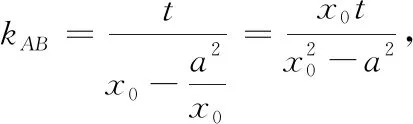
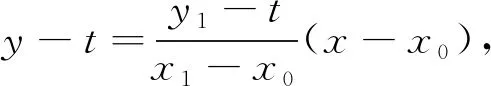
问题5上述在椭圆中的两个性质能否推广到双曲线呢？

圆锥曲线是由平面截圆锥而得.用一个不垂直于圆锥的轴的平面截圆锥，当截面与圆锥的轴夹角不同时，可以得到不同的截口曲线，它们分别是椭圆、双曲线、抛物线，它们往往具有类似的性质，故猜想在椭圆中的上述两个性质可以类比到双曲线.

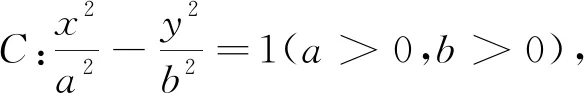
同样可以先利用GGB软件来验证，如图3，发现上述性质能推广到双曲线．证明如下：

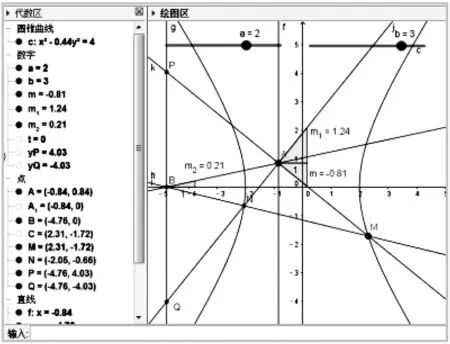
图3

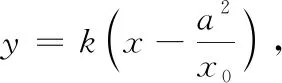
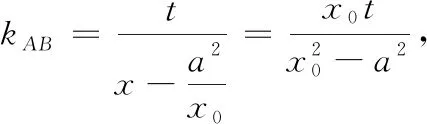
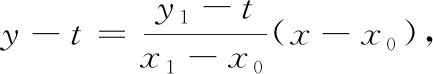
问题6上述性质能否推广到抛物线？

从特殊椭圆蕴涵的性质推广到一般椭圆中去，再将此性质由椭圆类比到双曲线，因为在椭圆和双曲线中焦点与其相应的准线与x轴的交点的横坐标之积都为a2，两者关系相近，容易进行类比推广.而抛物线只有一个焦点和一条准线，焦点与其相应准线与x轴的交点的横坐标互为相反数，这与椭圆和双曲线完全不同，无法直接进行类比.此时我们要深挖抛物线自身特点，由焦点与其相应的准线与x轴的交点的横坐标互为相反数出发，猜想A,B两点的横坐标也可能互为相反数．

性质3已知抛物线C:y2=2px(p>0)，点A为直线x=x0上的动点，若过点B(-x0,0)的直线l交抛物线C于M,N两点，直线AM,AN分别交直线x=-x0于点P,Q，则(1)kAM+kAN=2kAB；(2)BP=BQ．

同样可以先利用GGB软件来验证．如图4，发现上述性质能推广到抛物线．证明如下：

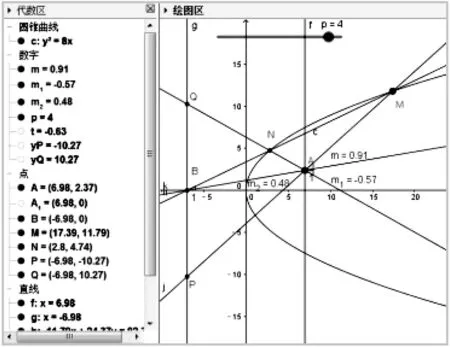
图4

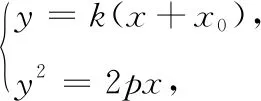
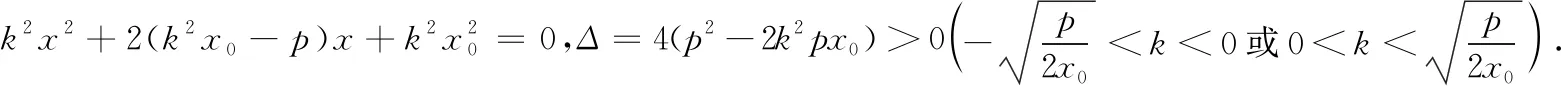
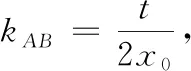
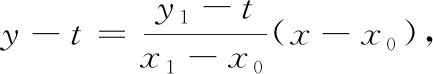
3 感受

通过GGB软件创设可视化教学情境，旨在克服数学知识的高度抽象性，建构一个数学探究场，不是将试题所蕴涵的性质直接抛给学生，而是由图形的直观到性质的猜想、实验、发现、证明，让学生亲历数学知识的发生过程，建构知识体系，把“看不透”“说不清”的一些性质通过动态形式呈现出来，使其清晰可见，实现教学的可视化．这能充分激发学生的探究热情，调动学生学习的积极性，提高学生课堂教学的参与度，把数学“冰冷的美丽”转化为学生“火热的思考”，促进其对问题的理解和对试题本质的认识，也有助于养成反思的良好习惯．

基于信息技术的教育资源和教学手段日新月异，正改变着教学方式．GGB软件能在“形”与“数”之间自由转换，突破数学因高度抽象概括的特性所带来的“只可意会、不可言传”的障碍，为改善数学的教与学提供极大可能，切实改进传统数学教学的不足，提高教学效率．《普通高中数学课程标准(2017年版)》的实施建议中明确指出，数学教师要努力提升数学教学实践能力，要提升信息技术的使用能力，实现信息技术与数学课程的深度融合．这要求数学教师要加强学习，掌握信息技术，勇于实践，也让学生逐步感受数学的奥妙，感悟数学的科学价值和审美价值，使学生逐渐养成会用数学眼光观察世界、会用数学思维思考世界、会用数学语言表达世界的习惯，不断提升其数学核心素养．