新课标视域下一题多解的教学设计审视

杨利刚 (江苏省苏州中学 215007)

数学解题教学是日常数学教学的一个重要内容和形式．所谓一题多解，就是通过多种方法解答同一道数学习题．数学解题中采用一题多解，具有较好的教学价值，因而成为我国中小学数学教师实施解题教学的常用方法和手段．

随着教育教学改革的推进和深化以及《普通高中数学课程标准(2017年版)》(下称《课标2017》)的出台和实施，教师需要认真学习、领会课标精神，将课标中数学学科核心素养的培养、发展落到实处．对于一题多解的教学实践，应当与时俱进地顺应新课标的理念要求，以更好发挥其应有的教学功能，更充分地体现其教学价值．

1 一题多解教学功能的思考和再认识

在数学解题教学中，选取一些有代表性的典型问题，引领学生多角度、多层次地展开解题探索和思考，从而获得多种解题的思路和方法，有助于学生对数学知识的理解和巩固，有助于学生感受、体悟数学知识间的联系，从而有助于对数学内容的整体把握和良好认知结构的形成以及对数学思想方法的领会和自觉运用．这对学生数学迁移能力的形成和发展、发散性思维能力的培养和提高，进而发展其数学学科核心素养也有着一定的作用．

2 新课标要求下一题多解的教学定位

《课标2017》指出，“依据数学学科特点，关注数学逻辑体系、内容主线、知识之间的关联．”“突出数学主线，凸显数学的内在逻辑和思想方法；高中数学教学以发展学生数学学科核心素养为导向，创设合适的教学情境，启发学生思考，引导学生把握数学内容的本质．”具体地说，通过一题多解的解题教学，可以实现对不同章节、不同内容的复习巩固，揭示不同章节数学知识之间的内在联系．同时，在一题多解过程中，分析、比较相应的解题方法，挖掘内隐的数学思想，能更好地呈现数学内容的本质．

3 新课标视域下一题多解的课堂实践及体会

习题是课堂教学内容的巩固和深化，为学生数学学习提供平台．对于复习课来说，复习题要关注知识的系统性，帮助学生理清数学知识的结构，使其整体理解、系统掌握学过的数学内容；要关注数学内容主线之间的关联以及数学学科核心素养之间的协调，帮助学生在掌握知识技能的同时，进一步感悟数学的基本思想，积累数学思维的经验．

下面结合一节高三数学复习课的课堂教学，从函数、数列、不等式、数学归纳法的内容主线谈谈新课标背景下“一题多解”的教学实践和体会．

选取的数学问题是：“证明：当n≥3,n∈N*时，nn+1>(n+1)n成立”．(教材习题)

(1)视角一：数学归纳法下的解题审视

对原问题作一些变更，呈现为：n∈N*，试比较nn+1与(n+1)n的大小，并探索是否存在一般性的结论.若有，写出该一般性结论，并予以证明；若没有，请说明理由．

课堂分析：引导学生先作特殊探索，尔后通过观察猜想是否具有一般结论．记f(n)=nn+1,g(n)=(n+1)n，n∈N*，展开如下探索：f(1)=12=1，g(1)=21=2，所以f(1)g(3)；f(4)=45=1 024，g(4)=54=625，所以f(4)>g(4)……根据上述探索，合情猜想：当n≥3,n∈N*时，有f(n)>g(n)．

由于上述猜想是一个与正整数有关的结论，学生自然而然地首先想到采用数学归纳法来证明.顺应学生的思路，接下来进行推导证明．

证明 ①当n=3时，f(3)=81>g(3)=64，即n=3时，猜想的结论正确.

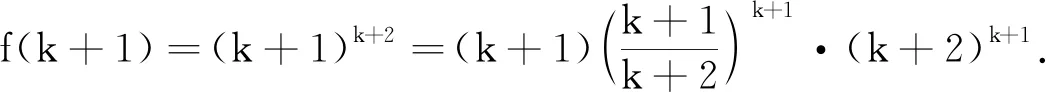
由①②可知，猜想的一般结论正确，即当n≥3,n∈N*时，有nn+1>(n+1)n．

说明将问题设问为当前形式，创设了一个探究的问题情境，由特殊到一般，然后归纳出一般结论，再用数学归纳法给出严格的逻辑证明，让学生历经探索、归纳、猜想以及数学证明的过程，这也是科学探索的一般过程．另外，证明过程中，由归纳假设推证n=k+1时，引导学生思考变形转化，突破解题难点即可．

(2)视角二：数列单调性下的解题审视

这是一个与正整数有关的不等式，联想两个数列{nn+1}与{(n+1)n}，那么问题可以表述为：“已知数列an=nn+1,bn=(n+1)n，求证：an>bn(n≥3,n∈N*)．”

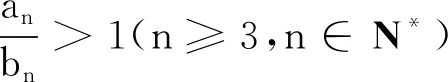
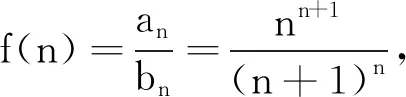
说明推导出数列f(n)的单调性，最后利用f(3)>1便可证得问题．同时让学生再次明确,数列单调性问题的处理是通过逐项传递来实现的，这不同于连续函数的单调性处理，这也体现了数列是定义在正整数集(或其子集)上的一类离散函数的数学本质．

(3)视角三：连续函数单调性下的解题审视

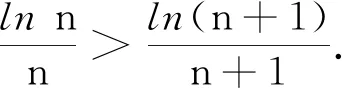
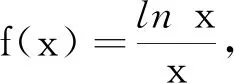
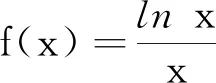
(4)视角四：重要不等式运用下的解题审视

证明 不等式nn+1>(n+1)n对n≥3,n∈N*成立．

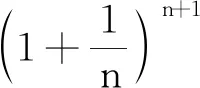
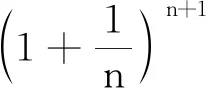
(5)视角五：数学高观点下的解题审视

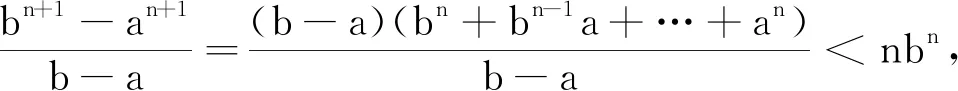
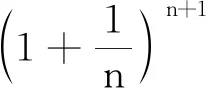
4 几点反思及教学建议

数学教学中，一题多解具有对所学知识加以融会贯通的作用，不仅体现了解题能力的强弱，更重要的是其具有开放式思维特点，是一种培养学生创新能力的重要思维方法．

通过一题多解练习，可以提高习题的利用率，进行集约化教学，发挥典型问题的最大教学价值，切实提高数学教学效率．

通过一题多解练习，有利于培养学生站在不同视角，对问题有整体认识的意识，有利于提高学生分析问题、解决问题的综合能力，达到熟练掌握知识和运用知识的目的，更重要的是可以培养学生的思维能力和创新精神．

通过一题多解练习，可以使学生更好地把握数学知识间的内在联系，培养学生正确的数学观，更加深刻地理解数学体系和逻辑结构．

当然，一题多解的练习要法乎自然，不要刻意追求.遇到合适的数学问题去展开一题多解的教学时，要在顺应学生的数学水平和思维能力，以及顺应学生基本想法的基础上循循善诱，引领学生拾级而上，使其数学能力迈上更高的台阶．