高考三角函数一轮复习策略思考——基于广东高考年报

邱志权 余铁青 (广东省中山市桂山中学 528463)

1 引言

纵观近年高考试题，结合各大主流联考试卷，都呈现出这样一个客观事实：三角函数部分知识内容的考查力度在增大．命题着力点依旧是对于三角函数图象性质和三角函数恒等变换的考查．具体包括其周期性、单调性、零点、最值、限定条件下的正余弦定理、二倍角公式、诱导公式、合一公式、面积公式等的考查．考查的知识内容越来越全面，命题在深度和广度上一直在挖掘延伸，对学生的思维能力要求逐年提高，整体正在从考查知识向考查能力转变．

2 高考数学三角函数内容实例分析

例1(2019年新课标Ⅰ卷文数第7题) tan 255°=( )．

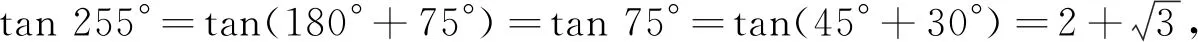
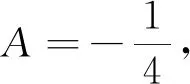
A.6 B.5 C.4 D.3

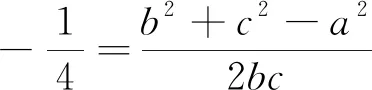
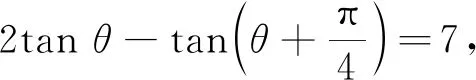
A．-2 B．-1 C．1 D．2

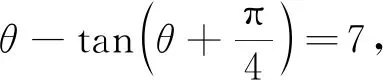
例2是典型的正余弦定理的混合应用，难度中等．学生应掌握角化边的应用，计算中发现两个方程有三个未知数，求解其中两个量的比例关系，这实际上是高等数学里面n元方程基础解系的三元情况．这与《普通高中数学课程标准(2017年版)》所提及的要在高中数学中渗透高等数学思想，考查学生进一步学习高等数学的潜力的初衷高度吻合．广东高考年报(2019)统计结果显示：该题平均分2.50，标准差2.50，难度0.50，区分度0.76，其中 156 104人选A，占比50.01%，53 924人选B,占比17.28%， 57 087人选C，占比18.29%，45 051人选D，占比14.42%．对比例1、例3，发现这两题与例2的得分大致一样，但从知识难度层面来讲，此题的难度是大于例1、例3的，因为这题的函数思维显然要求更高，造成这样的实际结果，只能说明学生对正、余弦函数的熟悉程度相较于正切函数而言更高，也说明学生的基础知识掌握不扎实．

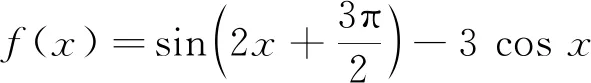
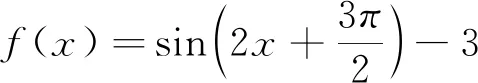
评注此题主要考查诱导公式，要求学生能够将整个函数解析式转化成同名三角函数，再利用二倍角公式进行角度上的化归，最后再结合换元法的使用将此题转化成一个求二次函数的局部函数图象的最值问题．整体而言对学生的转化能力要求较高，学生应熟练各部分之间的转化．广东高考年报(2019)统计结果显示：样本数312 463，平均分0.91，标准差1.93，难度0.18，区分度0.51．从统计数据不难发现这道题的得分率极低，然而从考查知识点的角度而言，难度不算大，只属于中等稍难题，这说明学生解决多知识融合问题的能力较弱，对很多知识无法进行整合、归纳，其知识模块相互孤立，没有形成必要的合力．

例5(2019年新课标Ⅰ卷理数第11题)关于函数f(x)=sin|x|+|sinx|，有下列四个结论：

①f(x)是偶函数；

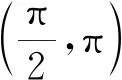
③f(x)在[-π,π]上有4个零点；

④f(x)的最大值为2．

其中所有正确结论的编号是( )．

A. ①②④ B. ②④ C. ①④ D. ①③

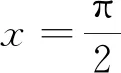
评注本题考查的知识点为三角函数的图象性质，主要集中考查奇偶性、单调性、零点、对称轴、最值等性质．随着高考开始考查多选题，此类试题的考查频率极有可能越来越高．广东高考年报(2019)统计结果显示：平均分3.75，标准差2.17，难度0.75，区分度0.50，具体情况为：选A 32 079人，占比9.36%，选B 29 786人，占比8.69%，选C 257 159人，占比75.02%，选D 23 751人，占比6.93%．此题处在选择题靠后位置，理论上讲应该是难度偏大题型，实际上考生答题比较理想，题干虽说有一些复杂，但是四个结论相对简单，只要掌握好图象基本知识，想要做对其实不难．

例6(2019年新课标Ⅰ卷理数第11题)△ABC的内角A,B,C的对边分别为a,b,c.设(sinB-sinC)2=sin2A-sinBsinC.

(1)求A；

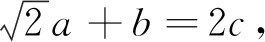
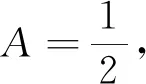
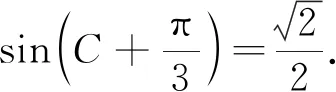
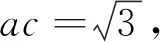
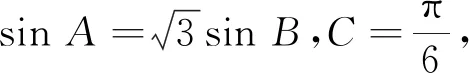
注：如果选择多个条件分别解答，按第一个解答计分．

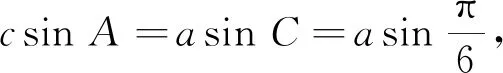
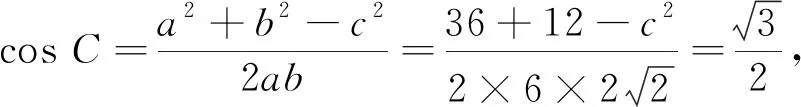
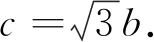
评注一方面，例6、例7都是正余弦定理的综合应用，要求考生能够运用正余弦定理进行有效的角边互化，整体难度不大，对学生的知识能力要求不高．在计算中可能出现多种情况的条件下利用内角和的隐含条件去除多余的情况，使得计算在有约束的条件下进行，有利于考查学生思维的严谨性．另外，例7是结构不良型问题，对学生选择策略的考查实际为素养的考查，考查学生在规定时间内根据已有知识作出妥善选择，选择最好的方法来求解．广东高考年报(2019)对例6的统计结果显示：平均分7.42，标准差3.86，难度0.62，区分度0.77．从以上数据可以发现学生的基本思路较清晰，从区分度看，学生大多都可以得分，也说明对简单的题加以练习，可使多数学生掌握，进而得分．

3 三角函数一轮复习建议

(1)认真研读考纲与高考年报等核心指导文件

一轮复习事关整个复习效率的高低，甚至可以说是一次彻底的大规模基础知识的回顾，该准确把握哪些重点、哪些难点、哪些要求掌握、哪里只要理解，都要根据指导性文件进行删选，确定重点复习方向，做到有的放矢．而每一年的高考学生所暴露出来的问题基本上是大同小异的，基于高考年报的统计数据基本是在一轮复习中后期才会发布出来的客观实际情况(一线教师很难在教育考试院改完卷立马拿到数据)，教师可以参考前一年的知识点，充分利用身边可用的教研资源，争取拿到与全国同时期最新的权威高考模拟试题，以便在复习中进行权衡、综合研判．

(2)复习过程切实做到回归课本

教材是什么？教材是学生学习新知识的最本原的载体．近些年教师圈出现了一个怪象，复习只用一本参考书而完全不用教材．这样做实际上与《普通高中数学课程标准(2017年版)》的指导精神背道而驰．事实证明，高考越来越重视教材的地位和作用．2019年全国Ⅰ卷三角函数模块的所有试题似乎都谈不上很难，但少有人清晰地意识到有不少试题其实来自于教材母题的演变，例如理科第17题的母型就是人教版高中数学必修1教材第18页的第3题．

(3)复习中注重基础思维的训练

数学究竟考什么？笔者认为是考查学生运用知识解决问题的能力．而解决问题效率的高低，甚至能不能解决问题最主要的还是思维的问题，像三角函数这块内容应注重化归与转化思想、分类讨论思想、数形结合思想、函数与方程思想等．这些思维能力的形成并非一蹴而就，它是日积月累慢慢形成的一种可持续发展的能力，因此教师在日常教学中一定要重视思维训练．

(4)复习中注重基础套路与变式教学相结合

三角函数模块的内容考查频率高，很多题可以说在平时训练中都见过甚至做过类似的题型，因此基础知识的积累就十分有必要了．一方面不必过于追求所谓的高难度题型，另一方面对于常规题型的解答套路，仍有必要渗透给学生，因为任何难题本质上都是若干问题的组合，基础知识的传授和常见套路的讲解是有必要的．另外，现在的高考题型多变，教师要注意到多模块知识的融合与串联，多多思考不变本质的变式教学．

(5)严抓书写与格式，养成规范好习惯

从广东高考年报和实际教学、批改试卷和作业的过程中，都反映出一个十分棘手的问题，学生经常出现自以为是的情况，在书写答案过程中肆无忌惮地跳步，有时甚至并未通过书写呈现自己的主干思维过程，或者因为急于求成而将一些重要信息遗漏以至影响最后的答案．例如换元后不书写新变量的定义域很可能造成最后结果的错误．这从侧面要求教师在日常教学过程中切不可只讲思路，而不注重对整体解答过程的板书，长此以往易使学生书写混乱，导致出现不必要的失分．