从一道检测题看解题的思维形态

陈 新 (江苏省苏州市苏州高新区第一中学 215009)

数学解题离不开基本知识、基本技能、基本思想和基本活动经验．在实际解题过程中，“四基”反映在正确有效的思维，特别是在限时的检测过程中遇到综合问题的时候，“四基”会反映在如何进行方法的选择、遇到困难时思维形态的转变及解题过程中信心的大小对解题的心理作用．本文试通过苏州市2019—2020学年第二学期高二学业质量阳光指标调研卷第21题的解答思维过程，分析解题时的思维形态，揭示思维的效能，以期在有限的时间内作出快速解答．

1 试题呈现

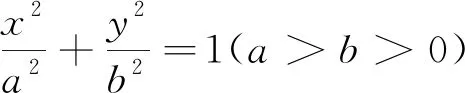
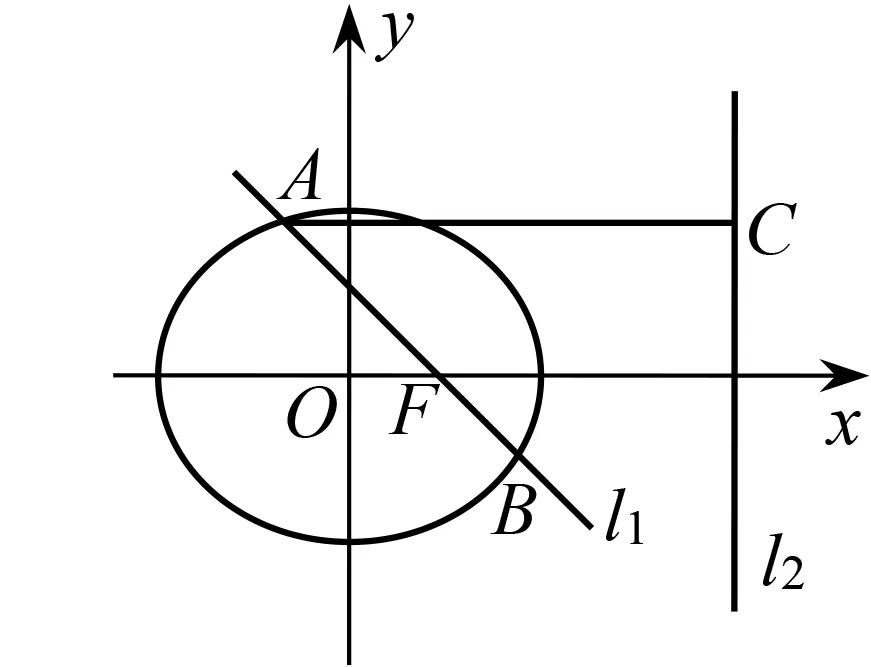
图1

(1)求椭圆E的方程．

(2)在x轴上是否存在一个定点T，使得B，T，C三点共线？若存在，求出T的坐标；若不存在，请说明理由．

2 解法探究

第(2)问是直线与圆锥曲线相交问题．按直线与圆锥曲线相交时定点问题的通性通法，基本的思维方式是设出直线方程与圆锥曲线方程构成方程组求解．然而直线方程的形式有多种，由基本经验知，直线过x轴上椭圆的焦点，可以将直线方程设为AB：x=my+1形式，其中m为参数，这样点A，B均可由参数m来表示，继而点C也表示了出来；再写出带参数的直线BC方程，若直线BC过x轴上定点T，则在BC方程中令y=0，即可求出点T的横坐标，它与参数m无关．这样就形成了解法1．

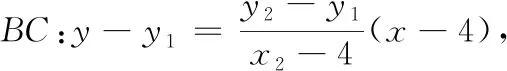
从解法1可以看到，没有一定的基本经验，用求根公式写出方程的解时会产生畏惧心理．另外，在写出方程的解后，用换元转化思想也需要一定的基本技能，不然用求到的根写出直线BC的方程会导致运算冗繁，对考生心理影响较大，易于受挫．

而事实上，在平时学习中更多的是运用韦达定理这一基本技能以减少运算，这是常用解法2．

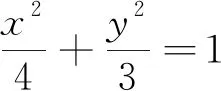
问题来了，(*)式含有y2-y1，4y2-y1，不能直接将韦达定理代入，怎么办？要用韦达定理，自然要想办法将(*)式变为y1，y2的和与积形式，这是个难点．在此应积极展开思维，从目标、式子的结构形式，展开联想和尝试．

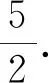
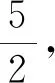
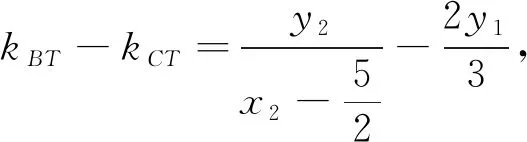
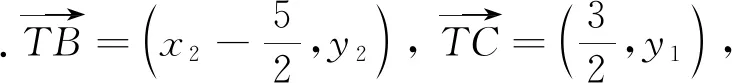
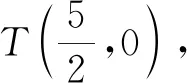
倘若没有想到上述方法，或想到而无法达到目的，是否可以从几何角度进行思考？也许这能让我们柳暗花明，思路豁然开朗．

图2

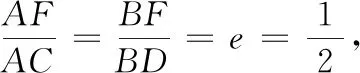
3 总结

纵观上述解题的思维形态，对于问题,我们必须正确辨清问题所涉及的知识与问题解决所需的基本方法，从基本知识和基本技能出发，冷静细心，敢于运算．遇到困难时，更需从基本经验、数学的基本思想出发，咬定目标，坚定信心，勇于联想，善于变通，才能攻坚克难．从核心素养的角度上讲，前者是模型的运用，谓“数学运算”，后者是创建模型，属“数学建模”．数学建模素养的达成较数学运算素养的达成更为困难，需要长期的借鉴与独立思考的过程，学生才能建立正确分析事物的方法，养成分析事物的习惯，达到解决问题的快捷与有效．