几何变换法让压轴题不再“压”你

陈金红 (湖南省常德芷兰实验学校初中部 415000)

张国平 (湖南省常德市教育科学研究院 415000)

中考压轴题让考生(也包括很多平时优等的学生)望题生畏，但突破现象看本质时可以发现，其实很多问题用“几何变换”便可解决．在初中阶段，包括平移、旋转、轴反射三种全等变换和相似、位似两种保角变换，其中前者在全国各地的中考压轴题中经常“神出鬼没”．本文结合2020年常德市中考压轴题给出我们的教学观察，让压轴题不再“压”你！

试题已知D是Rt△ABC斜边AB的中点，∠ACB=90°，∠ABC=30°，过点D作Rt△DEF，使∠DEF=90°，∠DFE=30°，连结CE并延长CE到P，使EP=CE，连结BE，FP，BP，设BC与DE交于点M，PB与EF交于点N．

(1)如图1，当D，B，F共线时，求证：①EB=EP，②∠EFP=30°；

(2)如图2，当D，B，F不共线时，连结BF，求证：∠BFD+∠EFP=30°．

图1 图2

图3

(2)如图3，延长DE到Q，使EQ=DE，连结CD，PQ，FQ．因为EC=EP，∠DEC=∠QEP， 所以△QEP≌△DEC(SAS)，则PQ=DC=DB.

因为QE=DE，∠DEF=90°,所以EF是DQ的垂直平分线，因此QF=DF．

又CD=AD，故∠CDA=∠A=60°，∠CDB= 120°，所以∠FDB=120°-∠FDC=120°- (60°+∠EDC)=60°-∠EDC=60°-∠EQP=∠FQP，从而△FQP≌△FDB(SAS)，因此∠QFP=∠BFD.又EF是DQ的垂直平分线，故∠QFE=∠EFD=30°，即∠QFP+∠EFP=30°，从而∠BFD+∠EFP=30°．

·教学观察

1.本题是三角形的综合题，考查了平行线分线段成比例、勾股定理、三角形全等的性质和判定等知识，解题的关键是正确寻找全等三角形，难度适中，属于中考常考题型．限于篇幅，这里只谈第(2)问．

2.标准答案给出了第一种几何变换“平移”法，即我们常说的“见中点等倍延长”法，那“轴反射”变换是否可行呢？答案是肯定的.

1）基于智能手机的师星学堂平台在一定程度上促进了学生课堂的参与度和课下的自主学习。如在学生访问次数上（图1），除了两次课上，学生积极参与课堂活动，访问次数多外，在课下的访问次数也相对较多；从学生上课活动量（图2）和课程任务完成情况（图3）的统计结果可以看出，一些学生能够积极参与课堂活动，也能够在课下及时查看课程学习资料、查看通知、完成学习任务等。

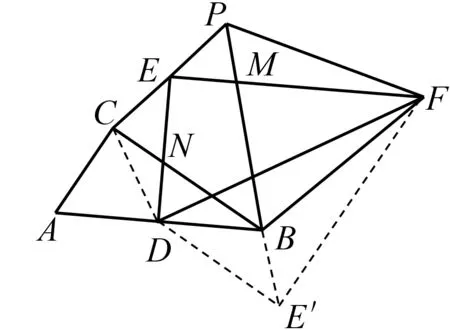
图4

如图4，将Rt△DEF沿DF作轴反射，得到Rt△DE′F,连结BE′．显然有EF=E′F，DE=DE′，∠EDF=∠E′DF=60°，∠EFD=∠E′FD=30°，∠DEF=∠DE′F=90°．

连结CD，在Rt△ABC中，D为斜边AB的中点，则DB=CD.又∠ABC=30°,则有△DAC为正三角形，且∠CDE+∠BDF=180°-60°- 60°=60°．

由DB=CD，∠CDE=∠BDE′=60°-∠BDF，DE=DE′，得△CDE≌△BDE′(SAS)，故BE′=CE=EP，并令∠CED=∠BE′D=α．

再由BE′=EP，∠BE′F=∠PEF=90°-α，E′F=EF，得△PFE≌△BFE′(SAS)，故∠EFP=∠E′FB．

在Rt△DE′F中，∠BFD+∠E′FB=30°=∠DFE′，于是∠BFD+∠EFP=30°．

更可发现FP=FB，∠PFB=30°+30°=60°，故△FPB为正三角形.亦即本小题可以改编为“求证:△FPB是等边三角形”．

3.上面用了平移、轴反射变换法进行了证明，那么“旋转变换”法是否亦可呢？答案仍是肯定的．

如图4，如果将△FPE绕点F旋转到△FBE′位置，想法是好的但又是不现实的，因为FP与FB的数量关系不明朗．因此舍弃整体保留“部分”旋转的方法，又结合结论必有∠PFB=60°，故“旋转变换”法具体是：线段FE绕点F逆时针方向旋转60°得到线段FE′，连结BE′，DE′，显然∠DFE′=60°-30°=30°=∠DFE，再加上EF=E′F，公共边FD=FD，可知△FDE≌△FDE′(SAS).以下与“轴反射变换”法完全类似．

综上可知，平移、旋转、轴反射变换法都可以解决问题，足见重视三种“全等”变换教学的重要性，同时由此也感受到了这三者间在运用时是相互通融的而不是彼此“观望”的．

4.其实此小题尽管图形变化了，有变化的结论如第(1)①小问，但第②小问与第(2)问其实本质是一样的．即当图2中的∠DFB=0°，即点D，B，F共线时(第(1)问条件)，30°=∠BFD+∠EFP=0°+∠EFP=∠EFP，即∠EFP=30°,正好是特殊情形！

5.其他方法概要展示

图5

方法1 如图5，作点F关于FD的对称点Q，连结DQ，CQ，EQ，CD，有∠EFD=∠EQD=30°，DQ=DF，可证得△PFE≌△CQE，得出PF=CQ.由CD=DB，∠CDQ=∠BDF=60°-∠ADQ，可得△QDC≌△FDB(SAS)，得到∠CQD=∠BFD，从而结论得证．

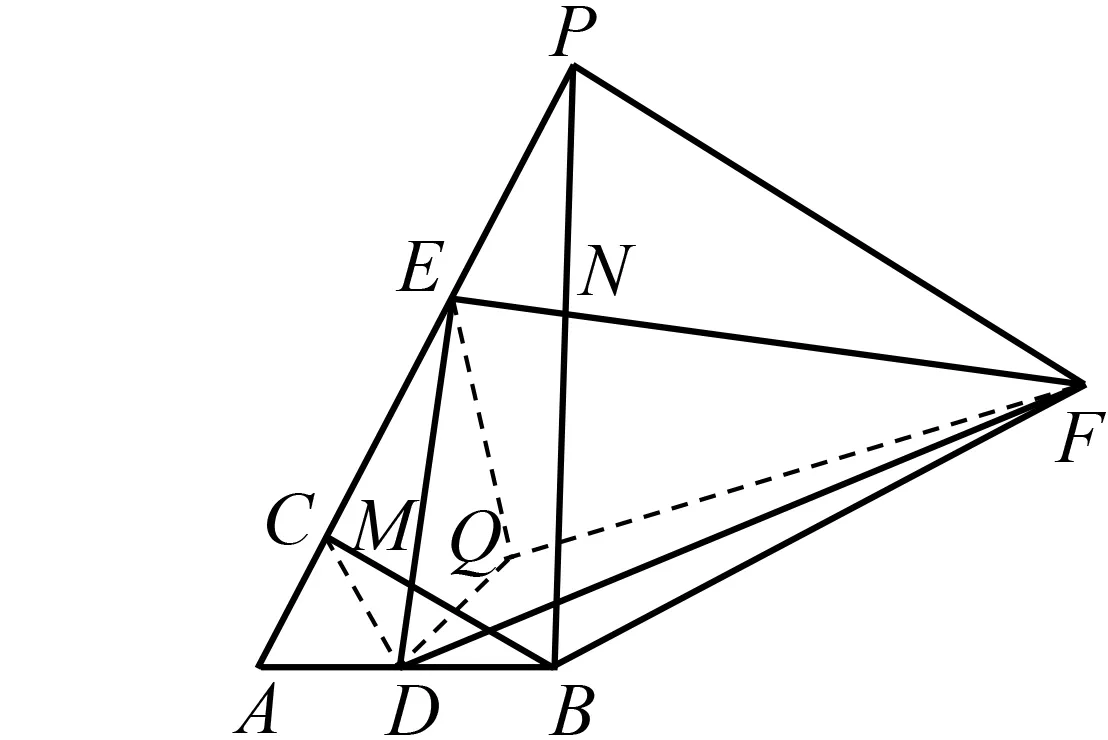
图6

方法2 如图6，作点P关于EF的对称点Q，连结DQ，EQ，FQ，CD，有△PFE≌△QFE，则∠PFE=∠QFE，PE=QE，∠PEF=∠QEF，进而有∠CED=∠QED，可证得△CED≌△QED(SAS)，得出DQ=CD=DB，∠CDE=∠QDE，有∠QDF=∠BDF，从而得出△QDF≌△BDF(SAS)，得到∠QFD=∠BFD，结论得证．

上面两种方法即作点关于直线对称的方法也就是“轴反射变换”的思路．

图7

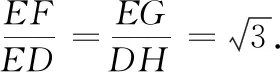
图8

上面两种方法即取线段中点的“三角形相似”方法,就是“相似变换”的思路．

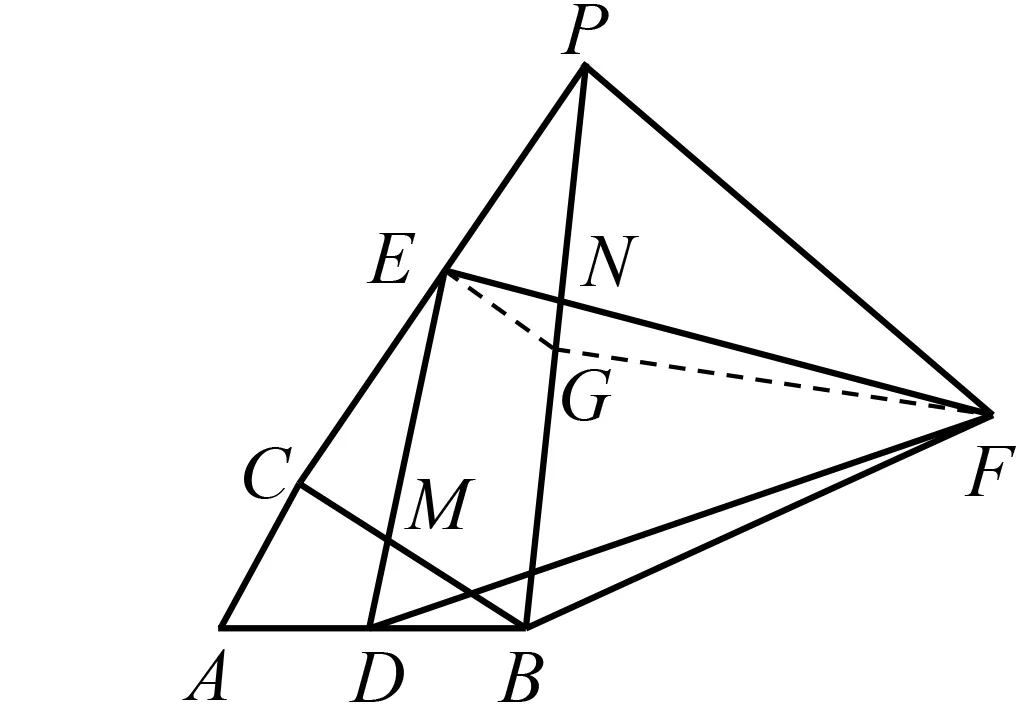
图9

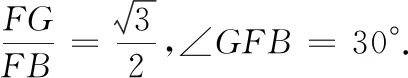
方法6 如图10，延长CD，使DQ=CD，连结BQ，PQ，可证得等边△BDQ≌等边△ADC.由ED是△CPQ的中位线，得出△PBQ≌△FBD，进而得出PB=FB，∠PBQ=∠FBD，所以∠PBF=∠DBQ=60°，因此△PBF是等边三角形，从而结论得证．

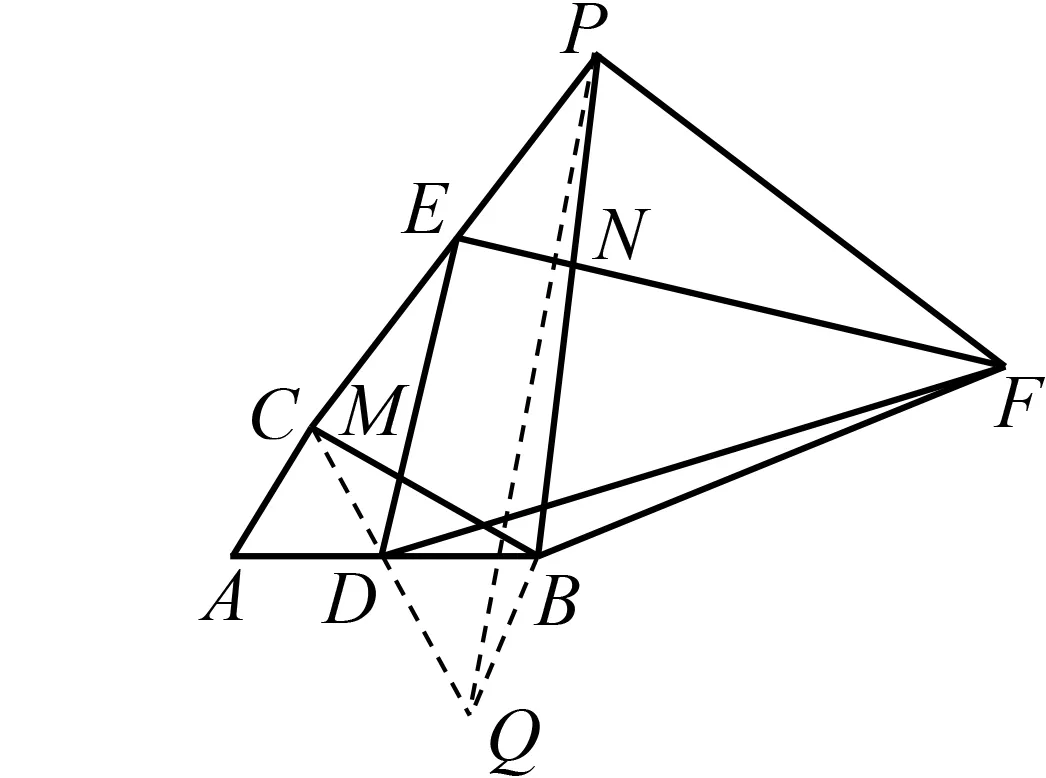
图10

上面两种方法即取线段中点(或见中点等倍延长)的“三角形全等”方法，就是“合同变换”的思路．

可见，图形变式有变化量，更有“不变量”，且正是“命题”的契机点，同时也在暗示几何变换方法就是解决问题的首要方法之一．由此我们也看到了题目中(1)(2)两问间的本质联系——特殊到一般．这也是突破压轴题教学不可忽视的一个重要环节，即教后反思“找联系”！恰当使用几何变换法完全有章可循，让压轴题不再“压”你，这其中既包括学生，更应该包括教者自己．