美英早期立体几何教科书中的类比思想*

纪妍琳 汪晓勤 (华东师范大学教师教育学院 200062)

1 引言

类比，是指由一类事物所具有的某种属性，推断与其类似的事物也具有相同或相似属性的一种推理方法．[1]历史上，阿基米德(Archimedes,前287—前212)通过类比得到关于球面积公式的猜想[2]；欧拉(L.Euler,1707—1783)通过将有限次代数方程的根与系数关系类比到无限次方程，从而解决了17世纪下半叶的著名数学难题——自然数倒数平方和[3]．类比在数学发现的过程中扮演着重要的角色，是一种具有创造性的数学思想．

以或然推理(归纳、类比)做出猜想，以必然推理(演绎)做出证明已逐渐成为数学教学中培养学生创新精神的重要方法．《普通高中数学课程标准(2017年版)》(以下简称《标准》)指出，类比推理是逻辑推理的一种重要形式．从《标准》的逻辑推理素养水平划分中提炼出类比推理能力的具体表现为：(1)能够在熟悉的情境中用类比的方法，发现数量或图形的性质、数量关系或图形关系，能理解类比是发现和提出数学问题的重要途经；(2)能够在熟悉的数学内容中识别类比推理；(3)知道通过类比推理得到的结论是或然成立的；(4)能够通过熟悉的例子理解类比推理的基本形式．[4]

根据《标准》，在数学教学中应该给学生创设通过类比获得数学发现的机会，揭示类比在数学发现中的创造性和类比推理结论的或然性，并基于实例帮助学生理解类比推理的基本形式．然而，高中数学中存在为“类比”而类比的形式化倾向，忽视类比推理的或然性，过于强调类比推理结论的唯一性，强调特定数学对象的类比等问题[5][6]．究其原因，一方面，教师所掌握的有关类比思想的教学素材十分有限；另一方面，随着HPM的教学理念受到越来越多的关注，HPM视角下高三数学复习课的教学也逐渐进入人们的视野，而复习课的教学往往需要以数学思想方法为主线展开．为此，我们需要针对类比思想开展深入的历史研究．

本文针对类比思想，对19世纪部分美英立体几何教科书进行考察和分析，从中总结出类比思想在定义、命题以及命题证明中的应用，以期为高中数学教学，特别是HPM视角下的复习课教学提供有用的素材和思想启迪．

2 定义中的类比

2.1 平面角与二面角

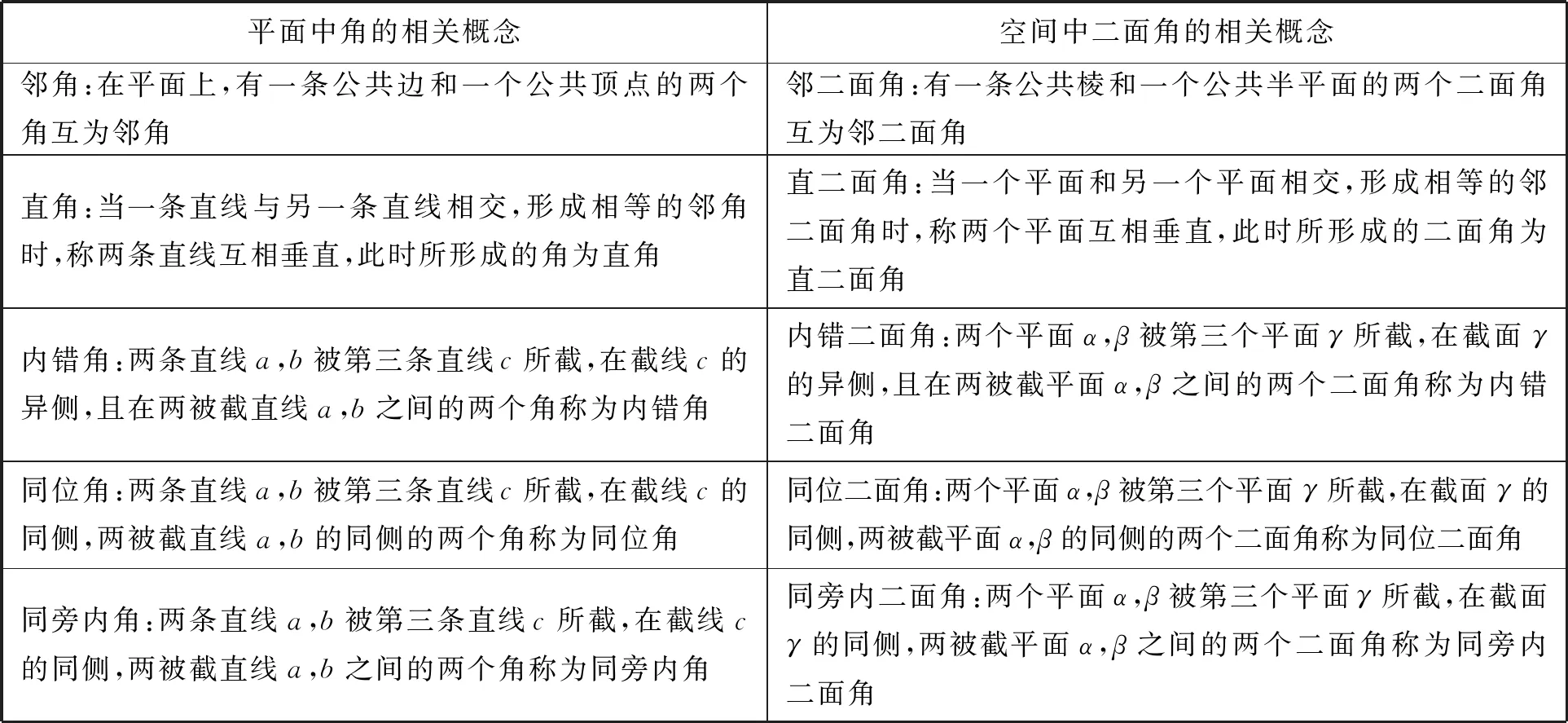
表1 平面角与二面角的相关概念[8]

二面角的概念与平面角的概念存在着相似性．有教科书指出，二面角的相关定义可以通过将平面角相关定义中的“直线”“射线”“顶点”分别替换为“平面”“半平面”“棱”得到．[7]例如，根据平面中的邻角、直角、内错角、同位角等角的有关概念，可以类比得到二面角的有关概念，具体内容见表1．

2.2 圆与球

圆是平面内到定点的距离等于定长的点的集合；球是空间中到定点的距离等于定长的点的集合．由于圆和球的相似性，有教科书设置练习，要求类比圆的有关概念，得到球的相应概念[9]．学生可以类比相切圆、圆的公切线和同心圆等概念，得到相切球、球的公切面和同心球等概念，见表2．

3 命题中的类比

3.1 平面角与二面角

一些教科书指出，二面角和平面角之间存在密切的联系，二面角的性质可以通过类比平面角的性质得到，见表3．

表2 圆与球的相关概念

表3 平面角与二面角的相关命题

图1 二面角的角平分面 图2 命题B2的反例

一些教科书要求学生类比平面角的有关命题得出二面角的相应命题[10][11]；大部分教科书在说明二面角与平面角之间的相似性之后，直接给出二面角的有关命题作为结论，不予证明[12]或将证明作为练习[13]．

类比具有或然性．在不加证明的情况下，早期教科书中由类比得出的关于二面角的命题并非全都正确．例如，表3中的命题B2就是一个假命题．事实上，在图2所示的情形中，平面α⊥平面γ，平面β⊥平面φ，满足命题B2的条件，若平面γ⊥平面φ，但平面α不垂直于平面β，则平面α与β所成二面角和平面γ与φ所成二面角既不相等也不互补．

3.2 卡瓦列里原理中的类比

17世纪意大利数学家卡瓦列里(B.Cavalieri,1598—1647)在《用新方法促进的连续不可分量的几何学》一书中提出一个定理，今称“卡瓦列里原理”．该原理包含平面和立体两种情形[14][15]：

夹在同一对平行线之间的平面图形，被平行于这两条平行线的任意直线所截，如果截得的线段的长度总是相等，那么这两个平面图形的面积相等；夹在同一对平行平面间的几何体，被平行于这两个平面的任意平面所截，如果截得的两个截面的面积总是相等，那么这两个几何体的体积相等．

其中，立体的情形(图3)就是我们耳熟能详的“祖暅原理”，最早由公元5世纪中国数学家祖暅所提出．

在早期立体几何教科书中，卡瓦列里原理的立体情形是作为研究几何体体积的重要定理出现的．有的教科书设置练习题，要求学生类比立体情形的卡瓦列里原理，得出“平面情形的卡瓦列里原理”[16]．有的教科书指出，学生在根据卡瓦列里原理进行类比推理时可能会得出以下命题[17]：

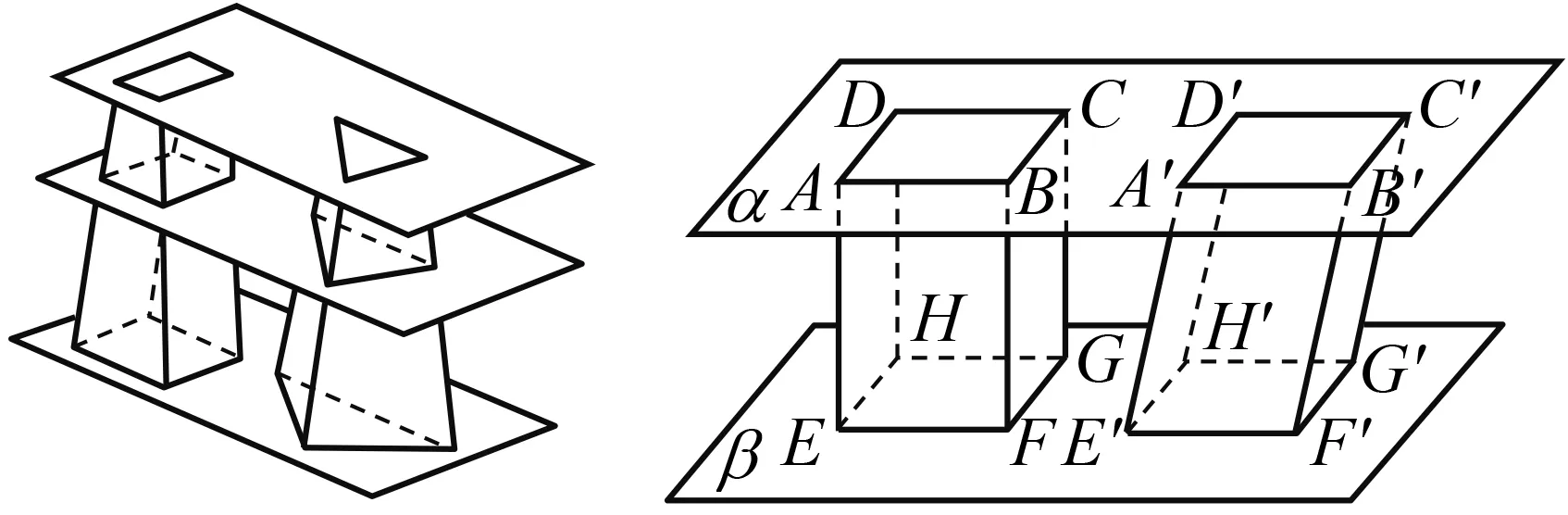
图3 卡瓦列里原理的立体情形 图4 类比卡瓦列里原理得出的假命题

夹在两个平行平面间的几何体，被平行于这两个平面的任意平面所截，如果截得的两个截面的周长总是相等，那么这两个几何体的侧面积相等．

事实上，我们可以举出上述命题的反例．如图4，长方体ABCD-EFGH和四棱柱A′B′C′D′-E′F′G′H′夹在平面α与β之间，其底面全等．用平行于α和β的任意平面γ截这两个几何体，所得截面的周长均与矩形ABCD的周长相等，满足上述命题的条件．设平面α与β的距离为h，则AE=h．若A′D′垂直于平面A′B′F′E′，则矩形ABFE与平行四边形A′B′F′E′面积相等，A′D′⊥A′E′．当A′B′与A′E′不互相垂直时，可得A′E′>h．由于AD=A′D′，因此矩形A′D′H′E′的面积大于ADHE的面积，此时四棱柱A′B′C′D′-E′F′G′H′的侧面积大于长方体ABCD-EFGH的侧面积．因此，上述命题是假命题．

在强调类比推理具有或然性的同时，教科书设置了相关练习题，要求学生举例说明类似的关于面积的错误结论．

3.3 圆与球

一些教科书设置练习题，要求学生通过类比先前学过的有关圆的命题，得出有关球的命题[18]，见表4．

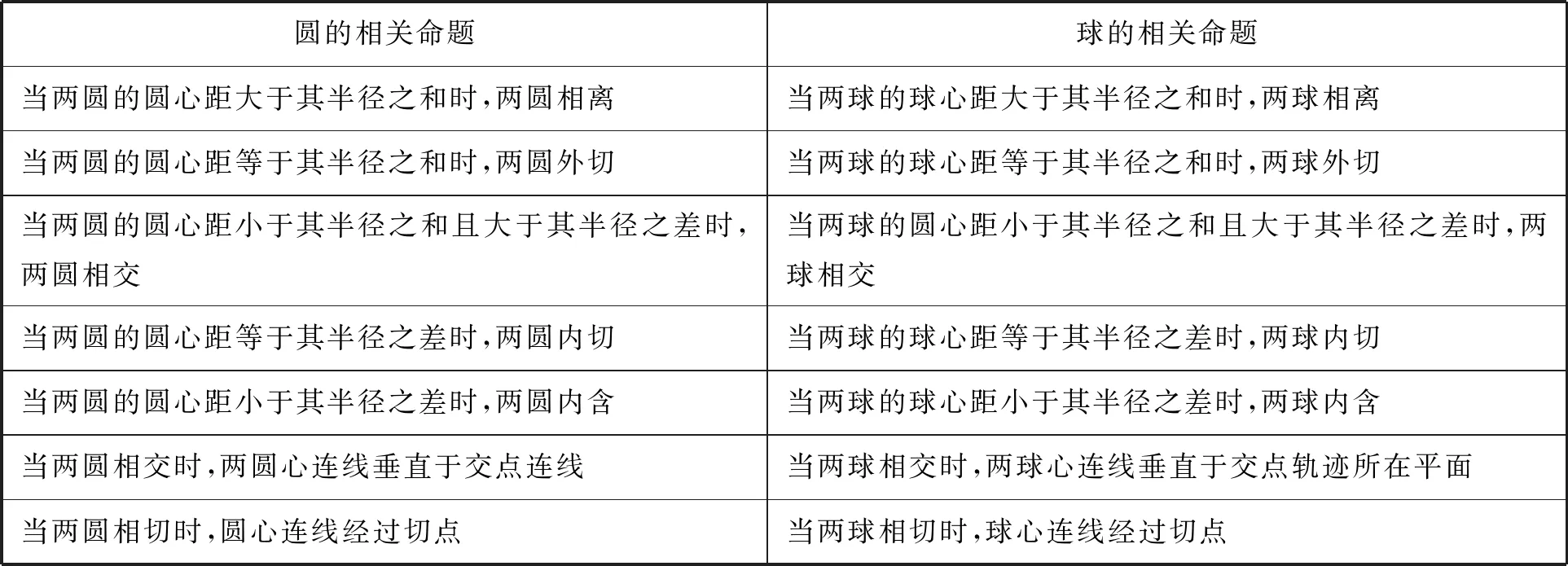
表4 圆的相关命题与球的相关命题

3.4 三角形与三面角

有公共端点并且不在同一平面的三条射线，以及相邻两条射线间的平面部分组成的图形叫做三面角．组成三面角的射线叫做三面角的棱，这些射线的公共端点叫做三面角的顶点，相邻两棱间的平面部分叫做三面角的面，相邻两棱所构成的角叫做三面角的面角，相邻两个面组成的二面角叫做三面角的二面角[19]．

早期教科书指出，关于三面角的许多命题可以通过类比三角形中的相似命题得出[20]．一些教科书指明，三面角中二面角和面角之间的关系，类似于三角形中角和边之间的关系，三角形的边对应于三面角的面角，三角形的角对应于三面角的二面角[21]．基于这样的对应，早期教科书给出了三面角的一些命题，见表5．

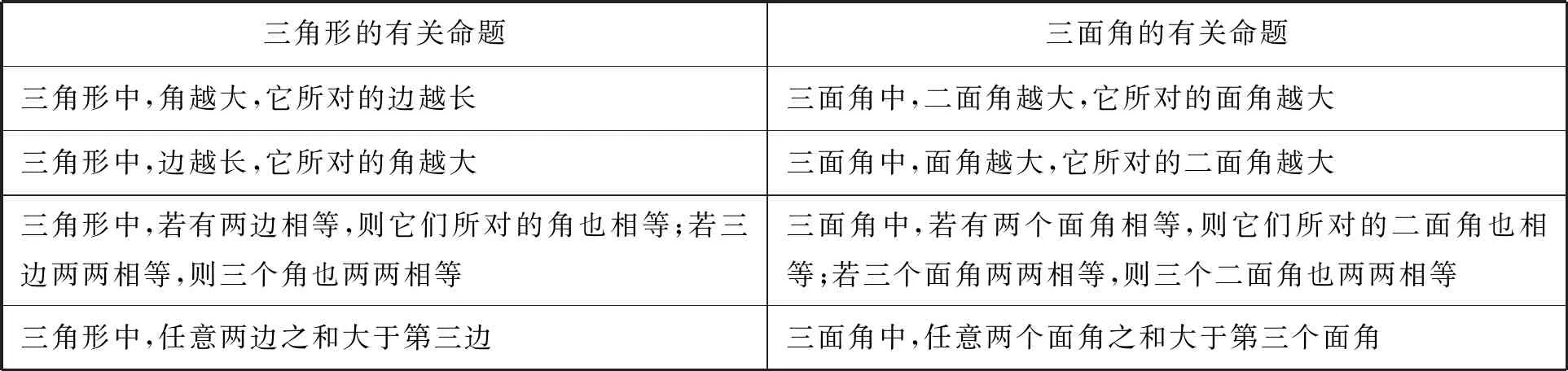
表5 关于三角形与三面角的若干命题

除了上述命题，三角形全等的判定定理等在三面角中也有对应的命题．部分教科书将三面角的上述有关命题作为定理或推论，部分教科书则设置练习题，要求学生类比三角形的有关命题，陈述三面角的类似命题[22]．

3.5 平行四边形与平行六面体

平行六面体是指六个面都是平行四边形的四棱柱．由平行六面体的定义可见，平行六面体与平行四边形之间存在着密切联系．由平行四边形的对角线相互平分，类似地有平行六面体的四条体对角线在各自的中点处相交[23]．类比平行四边形的一些性质，可得到平行六面体的相应性质．例如，在平行四边形中，两条对角线的平方和等于四边的平方和，通过类比，可以得到命题：“在平行六面体中，四条体对角线的平方和等于平行六面体十二条棱的平方和．”[16]这是一个真命题．

3.6 三角形与四面体

三角形是平面中边数最少的多边形；四面体是空间中面数最少的多面体．四面体的许多性质可由三角形的有关性质类比而来．例如，在图5中，△EBF和△ABC的面积之比等于(BE×BF)∶(BA×BC)．类比该结论可得到[24]：图6中的四面体O-ABC与O-A′B′C′的体积之比等于(OA×OB×OC)∶(OA′×OB′×OC′)．

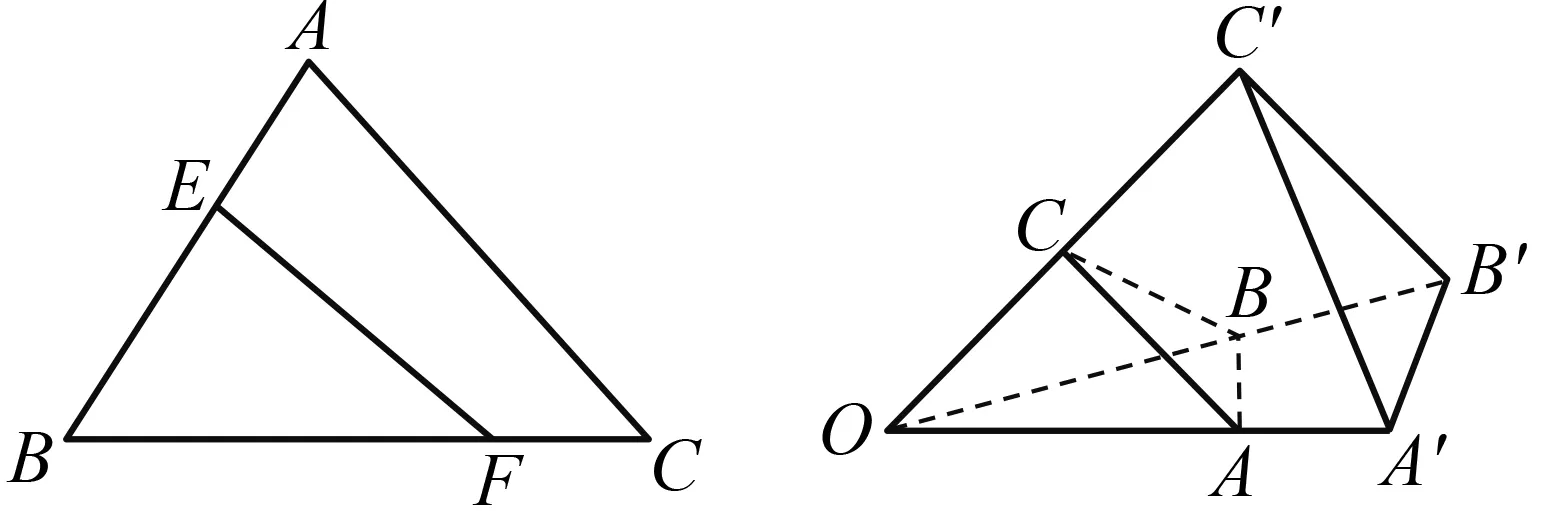
图5 三角形的一个命题 图6 四面体的一个命题

4 证明中的类比

4.1 三角形与三面角

由于三角形和三面角之间的相似性，有关三面角性质的证明，往往与三角形相应性质的证明相似，故可类比三角形性质的证明来证明三面角的相应性质．表6给出了三角形“等边对等角”与三面角“等面角对等二面角”的证明．

从表6中可见，只要将三面角性质证明中的字母V(三面角的顶点)去掉，就可以得到三角形相应性质的证明[20]．

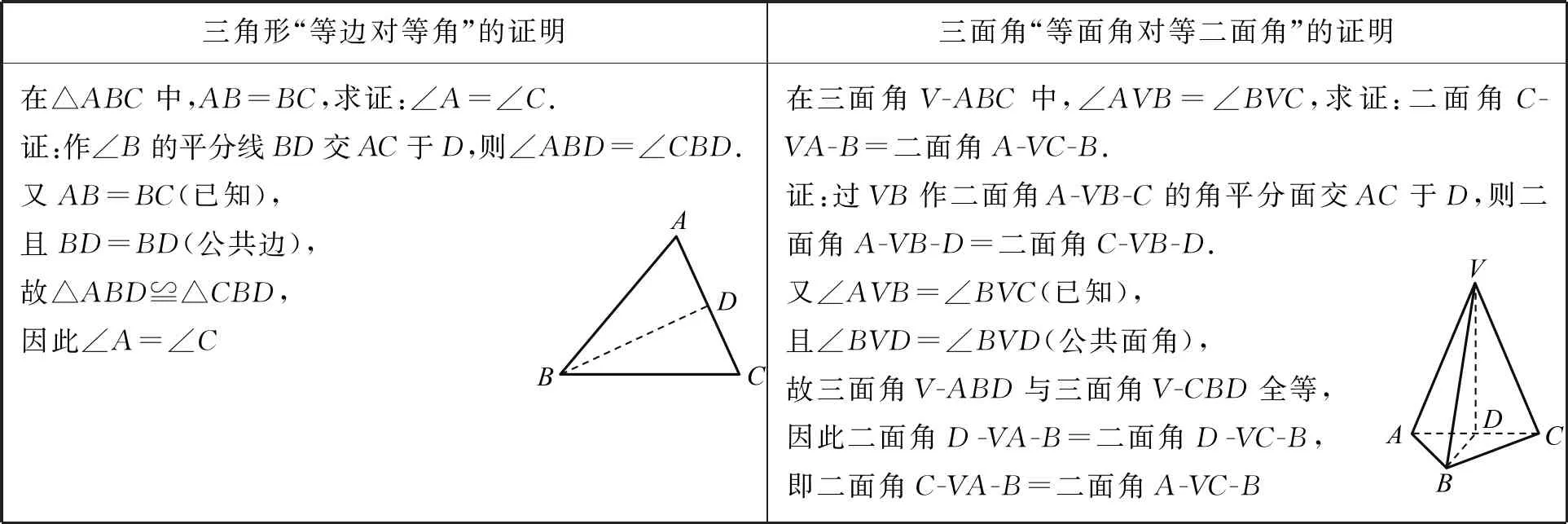
表6 “等边对等角”与“等面角对等二面角”的证明

4.2 平行线分线段成比例定理与平行面分线段成比例定理

在平面上，三条平行线截两条直线，所得的对应线段成比例．此命题即为平行线分线段成比例定理，可用相似三角形性质加以证明．将此定理类比到空间中，可得命题：“在空间中，三个平行平面截两条直线，所得的对应线段成比例．如图7，利用面面平行的性质和平行线分线段成比例定理可以证明该命题．

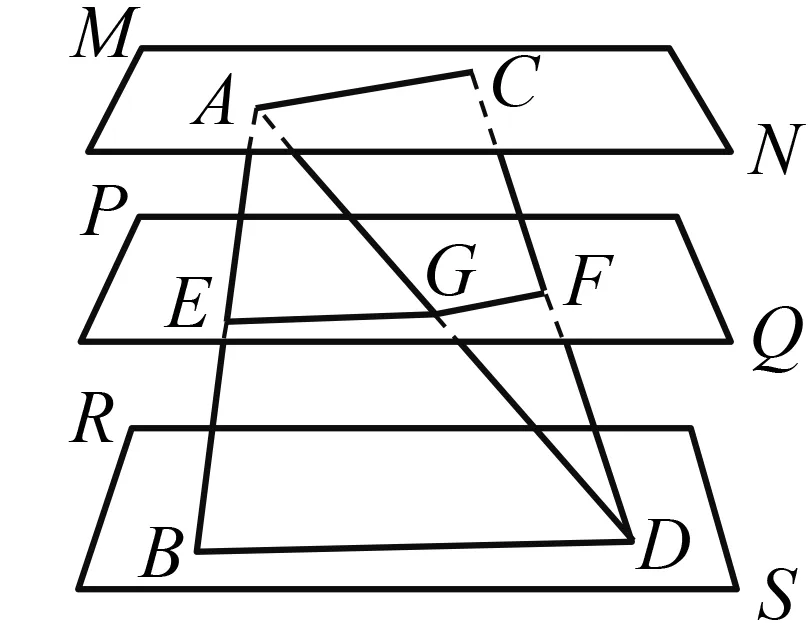
图7 平行面分线段成比例定理

平行面分线段成比例定理是平行线分线段成比例定理的一般化，两定理的表述非常类似．有早期教科书[15]给出平行面分线段成比例定理的证明后，提出思考题：两个命题十分相似，为什么平行面分线段成比例定理的证明，不类比平行线分线段成比例定理的证明呢？类比思想的运用往往基于不同数学对象之间的相似属性，而在解决问题的过程中，应该对数学对象的特有属性加以考虑，故不能盲目进行类比．教科书通过设置思考题，让学生在思考“为什么不进行证明方法的类比”这一问题的过程中，明晰平面与空间之间的差异．

5 教学启示

5.1 针对具体数学对象进行类比

美英早期立体几何教科书针对平面角与二面角、圆与球、三角形与三面角等具有相似属性的数学对象渗透类比思想．数学思想的培养应该以具体的数学概念、原理或证明作为载体，不能就“思想”谈“思想”．类比思想的渗透需要以合适的数学对象为载体，例如选取三角形与四面体、等差数列与等比数列、圆与椭圆等具有相似属性的数学对象，让学生在定义、定理和证明方法的学习过程中感受类比所具有的创造性．

5.2 借助多种方式培养类比思想

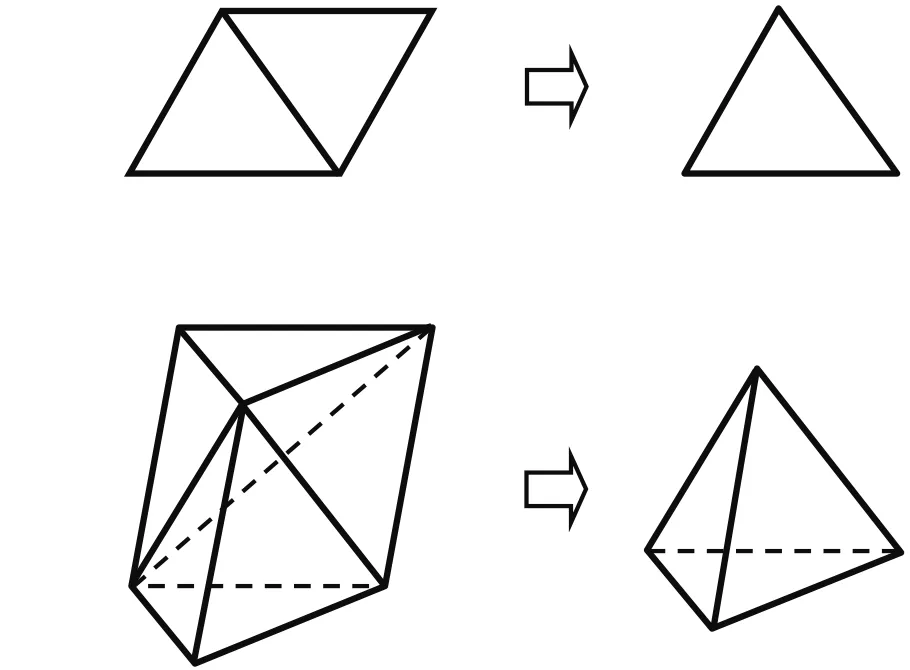
图8 三角形面积公式推导与三菱形体积公式推导

美英早期教科书在定义、命题和命题证明中渗透类比思想，学生根据教材的提示或要求，在类比旧概念得到新概念，类比熟悉的命题得出新命题，类比已掌握的证明方法证明新命题的过程中体会类比思想．今日数学教学中，教师可以在新概念、新命题或命题证明的学习过程中渗透类比思想．例如，在学习三棱锥的体积公式时，教师可以引导学生回顾推导三角形面积公式所用的方法，并将该方法类比到三棱锥中．如图8，平行四边形可以分割成两个全等的三角形，任意三角形可看作由与其等底等高的平行四边形沿对角线分割得到，故由平行四边形面积公式可推导出三角形面积公式．类似地，三棱柱可以分割成三个体积相等的三棱锥，任意三棱锥可被视为由与其同底等高的三棱柱分割得到，故由三棱柱体积公式可推导出三棱锥体积公式．

另一方面，许多美英早期立体几何教科书设置了有关类比推理的练习，今日数学教学中已较为少见．因此，教师在教学中也可从定义的类比、命题的类比推理和方法的类比三个角度入手，通过设置思考题、设计习题等方式渗透类比思想．

5.3 教学中揭示类比存在或然性

美英早期立体几何教科书中出现了通过类比得出的关于二面角的假命题，这充分说明类比推理的或然性．一些教科书强调，通过类比得出的命题可能是假命题，这一做法可资借鉴．学生在初学立体几何时，也常常会将平面几何中的命题不加限制地类比到空间中，从而得出错误结论．例如，将“平面中过已知点作已知直线的垂线有且仅有一条”类比到立体几何中，得到“空间中过已知点作已知直线的垂线有且仅有一条”的错误命题[1]．当学生出现类比错误时，教师应对学生运用类比思想的行为给予肯定，同时指明类比推理具有的或然性，让学生明确类比推理所得的结论很可能是错误的，必须借助演绎证明才能证明数学发现的正确性．