热轧宽厚板异步轧制力能参数建模与分析

卫垚宇，甄 涛，黄金博，李 恒，王 萍，江连运

(太原科技大学 机械工程学院，山西 太原 030024)

0 前言

宽厚板作为国民经济建设不可缺少的钢材品种，广泛用于压力容器、海洋平台、舰艇、坦克装甲和工程机械等领域[1]。高品质热轧宽厚板需求量旺盛，催生新一轮研究热潮，在众多研究中，轧制压力的准确预报是轧机设备校核、主电机容量选择以及生产工艺制定的依据，是厚板轧制不可缺少的重要任务[2-4]。

薄带钢异步轧制生产中进行的组织性能检验已表明，与同步轧制相比其晶粒得到细化，说明异步轧制可提高心部变形。一些学者对异步轧制过程中的轧制力进行了研究，张杏耀等[5]模拟了高异速比条件下的异步轧制过程，并对轧制力进行了分析研究。田勇等[6]分析了道次间冷却工艺参数对轧制力的影响规律。甄涛等[7]采用主应力法计算了宽厚板同径异速下蛇形/差温协同轧制的力能参数，对比模拟结果分析了各工况对力能参数的影响，但关于能量法对宽厚板异步轧制轧制力和轧制力矩进行理论建模方面的研究却少见报道。

小林史郎于1973年最先由刚塑性第一变分原理得到了板坯轧制功率泛函的刚塑性有限元矩阵表达式，开辟了刚塑性有限元解法[8-9]。其后，随着计算机技术的发展，有限单元法在轧制成形工艺和理论研究中获得诸多研究成果[10-11]；王雪松等人[12]建立了考虑纵横向应力分布影响的有限元模型；Kim等人[13]建立了考虑板带初始变形影响的有限元模型；张金铃和崔振山[14]建立了轧制力能参数的热力耦合模型，章顺虎等人[15]引入了变形渗透系数，建立了基于变分法的特厚板轧制力的理论模型，黄长清等人[16]研究铝合金热轧过程，建立轧制力模型并开发了轧制力预测系统。这些研究成果为热轧板带钢的深入研究提供了良好的基础。

尽管以有限元为基础的数值计算对轧制功率求解卓有成效，但数值解法仅能针对某一种或者某几种具体工艺参数计算出离散结果，无法从理论角度说明轧制力、轧制力矩与各工艺参数间的关系。实际上，数值解与解析解既相辅相成又对立统一，唯有二者协同发展才能推动成形理论的全面进步。因此，本文按照Von Mises屈服准则计算了相应的比塑性功率(即单位塑性功)，从异步轧制二维速度场与应变速率场入手，采用能量法获得了相应的内部变形功率、摩擦功率以及剪切功率，建立了基于能量法的宽厚板同径异速轧制力与轧制力矩理论模型。

1 异步轧制建模

根据宽厚板轧制的特点，在力能参数建模时进行假设。

(1)宽厚板的宽厚比很大，宽展相对很小，可以忽略不计，将其可以简化为平面应变问题；

(2)与板材相比工作辊的变形量很小，可以忽略，将工作辊设置为刚体；

(3)所轧制的材料符合Von Mises屈服准则，轧件轧前保持平直；

(4)上、下工作辊的直径相同，上工作辊的线速度小于下工作辊的线速度。

1.1 塑性变形区几何关系

图1为宽厚板异步轧制塑性变形原理图。图1中，H为轧件入口厚度，h为轧件出口厚度，R为工作辊半径，O点为工作辊中心，x为横坐标轴，y为纵坐标轴，vH为入口速度，vh为出口速度，θ为咬入角，α为变形区内任意一点对应的上工作辊角度，γ1为上工作辊中性角，γ2为下工作辊中性角，xn1为上工作辊中性角对应的变形区长度，xn2为下工作辊中性角对应的变形区长度，l为变形区长度，ha为α角对应的变形区内轧件厚度，A点为上工作辊的中性点，B点为下工作辊中性点。

图1 变形区示意图

根据图1中的几何关系可获得变形区长度l的计算公式。

(1)

式中，Δh为压下量。

由于同径异速异步轧制的咬入角度一般小于30°，根据雷军义等[17]对厚钢板轧制咬入条件的研究，在该范围内接触弧与二次抛物线轮廓非常接近，可将接触弧简化为抛物线。此时，上、下工作辊的轧制压下量Δh1、Δh2与总压下量Δh可表示为

(2)

变形区内任意断面轧板的厚度hx可通过图1中上工作辊与轧件接触面间几何关系表示为

(3)

式中，hx为变形区内任意断面轧板的厚度。

1.2 塑性变形区速度与应变关系

由于宽厚板忽略宽展，根据秒流量相等的原理有

vhhB=vHHB=vxhxB=U

(4)

由于轧制时金属流动为平断面且无宽展变化，联立方程(1)～(4)，并将其代入Hill速度场[18]，可得到上工作辊接触表面任意位置的速度分量为

(5)

式中，vx、vy、vz分别是轧制方向、厚度方向和宽度方向的速度分量，根据几何方程可知该应变球张量中各方向的应变速率为

(6)

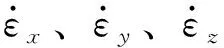
(7)

1.3 Mises屈服准则

变形区内任意一点服从Von Mises屈服准则，平面应变条件下可得

(8)

根据弹塑性力学理论，将公式(6)代入公式(8)求得Von Mises屈服准则下的单位塑性功为

(9)

2 轧制力能参数建模

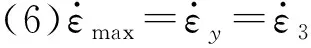
(10)

(1)上工作辊接触面摩擦功率。上工作辊和轧件接触面上消耗的摩擦功率为

(11)

(2)下工作辊接触面摩擦功率。下工作辊和轧件接触面上消耗的摩擦功率为

(12)

由于变形区出口截面上不消耗剪切功率，只有入口截面上消耗剪切功率，因此，该剪切功率为

(13)

根据上下工作辊异速比a，可以得到

(14)

总功率表达式为

W=Wi+Wf1+Wf2+Ws

(15)

将总功率W分别对上工作辊中性角γ1与下工作辊中性角γ2进行偏导,令∂W/∂γ1=0,∂W/∂γ2=0, 求得中性角γ1,γ2与其他变量间的关系式为

(16)

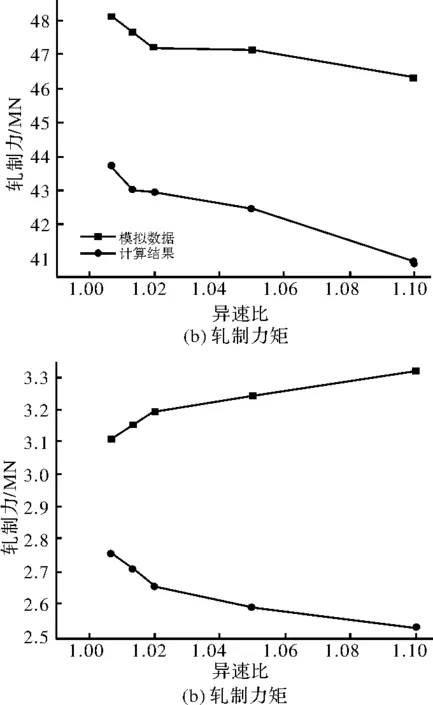
考虑到中性点位置的变化，轧制变形区的三个区域可能不会同时存在，当d

由于能量法计算中不涉及力的边界条件与平衡方程，在对轧制变形区的组成状态进行判断后，无需修改前述功率计算公式(15)，将式(14)代入式(16)，可获得各种摩擦条件下的总功率的最小值。轧制力矩、轧制力可按照式(17)确定。

(17)

式中，χ为力臂系数，一般对于热轧χ数值大约为0.5。

3 结果讨论与分析

F.Afrouz利用ABAQUS软件对非对称复合板轧制过程进行了数值模拟，并与其他研究者的实验结果和数值计算结果进行了比较，两者吻合良好，证实了有限元模拟结果的准确性[19-20]，基于此，文中采用有限元结果间接验证理论计算结果的准确性。ANSYS LS-DYNA作为显示动力学分析有限元软件，可以用于金属塑性成形模拟，因此使用该软件模拟同径异速异步轧制过程，模拟所需数据如表1所示。

表1 理论和数值计算用参数

根据表1中的数据，采用有限元模拟和理论计算的方法，分析了宽厚板的轧制过程，获得了不同异速比和压下率时的轧制力和轧制力矩结果，分别如图2～图3所示。

图2 压下率为16%时异速比-力能参数关系曲线

图3 压下率为12%时异速比-力能参数关系曲线

图2为压下率16%，且前滑区、后滑区和搓轧区同时存在时异速比-力能参数关系曲线。从图2中可以看出，随着异速比的增加轧制力逐渐降低，低速辊的轧制力矩逐渐变大，高速辊的轧制力矩逐渐变小。这是因为随着异速比的增加，低速辊(上工作辊)对应的中性点向出口移动，高速辊(下工作辊)对应的中性点向入口移动，变形区中前滑区与后滑区长度减小，搓轧区长度增大，轧件受到的剪切作用增强，从而使得轧制力下降，低速辊(上工作辊)轧制力矩逐渐增加，高速辊轧制力矩(下工作辊)逐渐减小。

图3为12%压下率时异速比对力能参数与的影响情况。随着异速比的增加轧制力逐渐降低，低速辊的轧制力矩逐渐变大，高速辊的轧制力矩逐渐变小，与图2呈现相同的变化趋势。

对比模拟数据与理论计算数据，当压下率为16%，异速比为1.006 7时理论计算结果与模拟结果偏差最小，最小相对偏差为5.67%，当压下率为12%，异速比为1.1时理论计算结果与模拟结果偏差最大，最大相对偏差为9.02%。证实了采用能量法所建立的轧制力能参数模型计算结果的准确性。

4 结论

(1)根据宽厚板轧制变形特点，对三维速度场进行简化，获得了适合于宽厚板同径异速异步轧制的二维速度场，并采用能量法，建立了宽厚板异步轧制力能参数计算模型。

(2)采用有限元方法模拟了不同压下率和异速比时宽厚板异步轧制过程，获得了压下率与异速比对轧制力矩和轧制力的影响规律，同时验证了理论模型的准确性，计算结果表明，理论计算结果与有限元模拟结果的最小相对偏差为5.67%，最大相对偏差为9.02%。