新型无键联接锁紧环设计与数值模拟

王 博，王建梅，余晓锁

(1.太原科技大学 重型机械教育部工程研究中心，山西 太原 030024；2.武汉正通传动技术有限公司，湖北 武汉 430301)

0 前言

我国目前正处于机械工业调结构、转方式、产业升级的重要时期以及机械工业实施制造业“强国战略”的重要阶段。传动联结件核心技术的突破是确保制造业“强国战略”目标实现的一环，而高性能、高可靠性是传动联结件的发展趋势。传统的传动联接件一般采用有键联接，该结构存在主轴上应力集中严重、对主轴的强度削弱较大、制造和装配工艺要求高、拆卸比较困难等问题。而无键联接结构简单、应力集中小、不削弱主轴强度,且对中性良好、便于装卸[1]。国内学者对联轴器、锁紧盘、胀紧套等无键联接件结构的设计制造进行了大量研究。张锋[2]介绍了一种新型胀紧联接套的结构原理、形式以及设计、制造加工要点，对该系列产品设计制造水平以及应用具有积极而现实的意义；何章涛[3]等对发电机组主轴胀套连接的结构强度进行了分析，为风力发电机组主轴胀套连接的结构设计分析提供了一个更为准确的分析思路；易柳峰[4]提出了一种新型无键式膜片联轴器的结构并运用有限元技术进行了应力分析和结构优化；滕瑞静[5]等结合有限元法和BP神经网络各自的优势，对圆柱面过盈连接的力学特性及设计方法进行了研究；王建梅[6-7]为提高多层过盈联接件的使用性能和工作可靠性, 以锁紧盘为研究对象，基于传统设计方法提出了一种新的设计方法；张颖艳[8]等通过建立圆锥面过盈联接的有限元分析模型，得到了不同过盈接触状况和结合长度对结构联接应力与联接动态性能的定量影响，对圆锥面过盈联接件的结构设计提供了一定参考；张迅[9]等应用ANSYS/PDS模块对风电齿轮箱收缩盘传扭联接性能和结构件强度进行了分析，对此收缩盘可靠性设计具有一定的指导意义；宁可[10-11]对多层过盈联接锁紧盘可靠性稳健设计进行了研究，为多层过盈联接可靠性稳健设计提供一定的指导和帮助。但是，以往对无键联接的结构研究一般针对锥体薄壁结构。这种结构公差较大，配合精度低，危险处应力集中严重，安装要求高，组装和拆卸难度大。本文提出了一种新型的锁紧环结构，公差小，配合精度高，危险处应力集中较弱，安装要求较低，便于组装和拆卸。

1 结构和工作原理

该锁紧环整体外观为M形，中间位置铣有U型槽，内部铣有两条对称的周向窄槽。工作时，使用锁紧螺钉启动轴向锁紧，实现了统一的横向收缩，由于锁紧环特殊的几何形状，周向窄凹槽升高，扩大外径，减小内径，与主轴和外环形成必要的接触，以传递扭矩和轴向力，从而实现可靠联接。由于锁紧环采用的是圆柱面，公差很小，配合精度高，联接很容易组装和拆卸。图1为锁紧环结构原理图。图中Ft为由锁紧螺钉拧紧时产生的轴向力；Fr为锁紧环对主轴及外环的径向压力；l1为顶端距/底端距；α为U型槽斜边角。

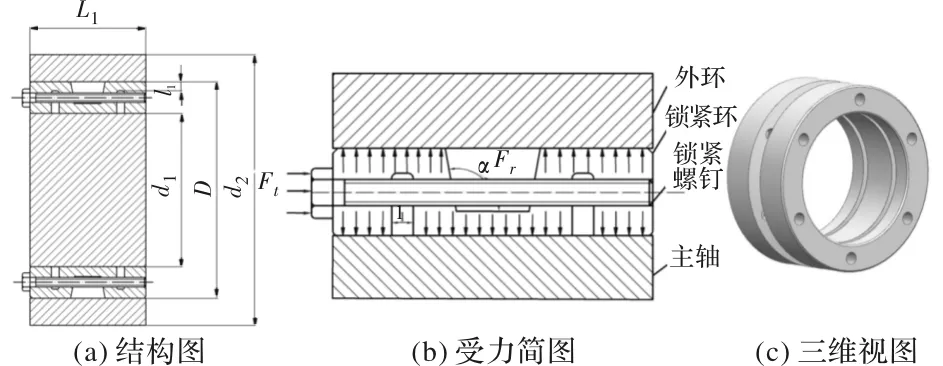
图1 锁紧环结构原理图

2 解析算法

2.1 锁紧环最小转矩

计算由拧紧力矩产生的轴向力[12]：

(1)

式中，n为螺钉个数；MA为螺钉拧紧力矩；d为螺钉直径；k为扭紧力系数，取值范围0.19～0.25。

轴向力Ft在主轴上产生径向接触压力[13]：

(2)

式中，L为轴与紧环的接触长度；f为轴与锁紧环接触面摩擦系数；d1为主轴直径;L=L1-2l(L1为锁紧环轴向长度，l为内部窄槽宽度)。

锁紧环最小转矩[13]：

(3)

2.2 锁紧环最大转矩

锁紧环内表面所受最大压应力、切应力和弯曲应力分别为

(4)

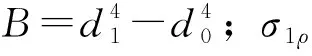
锁紧环内表面合成应力：

(5)

式中，σs为锁紧环材料屈服应力。

由式(4)、(5)可得锁紧环最大转矩：

(6)

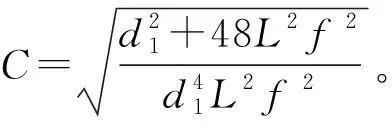
2.3 锁紧环强度校核

主轴承受的接触压力为

(7)

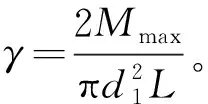
锁紧环和主轴接触面所受最大压应力和最大拉应力为

(8)

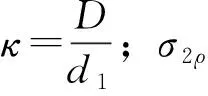
计算合成应力并校核锁紧环材料屈服强度为

(9)

3 有限元仿真分析

3.1 模型的建立

通过UG软件绘制三维几何模型。其尺寸参数如表1。为了有效提高建模、划分网格及计算的效率,适当简化部分模型[14]。考虑到各配合接触面之间均建立了接触对，接触面积较大，而接触问题是一种高度非线性行为,需要较大的计算资源。若再将锁紧螺钉考虑到分析当中将会使问题变得更复杂,故这里采用省略锁紧螺钉及锁紧螺钉孔的简化方法[1]。仅建立外环、主轴及锁紧环模型。为了得出该锁紧环可靠性影响因素，本文分别从U型槽斜边与底边的夹角(简称U型槽斜边角)、内部窄槽顶端与锁紧环外表面距离(简称顶端距)与U型槽底端与锁紧环内表面距离(简称底端距)及内部窄槽宽度三个方面建立模型，模型结构参数如表2。

表1 模型尺寸参数

表2 锁紧环结构参数

3.2 有限数值法

通过Abaqus有限元软件对模型仿真分析。外环及锁紧环的材料为42CrMo,屈服强度930 MPa,弹性模量为212 GPa,泊松比为0.28。主轴的材料采用40Cr，弹性模量为211 GPa,泊松比为0.277。各配合接触面之间的接触摩擦力设定为0.1。对轴两端及外环外表面分别进行固定约束，并在锁紧环左右端面施加轴向挤压力, 使其对主轴产生压紧效应,进而达到锁紧效果。模拟过程中，由于材料变形较大，分析过程中开启了大变形。在锁紧环的关键位置进行截面分割处理后，对各部件进行网格划分，最终得到28 644个单元，17 678个节点。网格模型如图2。

图2 网格模型图

4 结果分析

通过Abaqus对模型进行静力分析，得出各组锁紧环模型等效应力云图，见图3、图5、图7。锁紧环内表面及主轴外表面为锁紧环与主轴的作用面，为精确分析锁紧环传递至主轴的接触压力分布情况，对主轴外表面选取合适路径，采用参数化分析方法提取主轴路径上的数据点，绘制相应的接触压力曲线图，并与解析值进行比较。图4、图6、图8为主轴外表面接触压力在轴向位置的分布情况。

4.1 U型槽斜边角组锁紧环等效应力、接触压力分析

对A1-A3三组有限元模型进行分析。由图3应力云图趋势可知，随着U型槽斜边角增加，锁紧环的最大等效应力逐渐降低，应力集中位置主要分布在U型槽斜边角及内部窄槽处。从表3可知，A2、A3最大等效应力小于屈服强度，A1最大等效应力虽然达到了936.3 MPa，但介于屈服强度和抗拉强度之间，锁紧环所受应力仍然是安全的。值得说明的是，造成A1最大等效应力超过屈服应力的其中一部分原因可能是在分析过程中，忽略了螺钉，用对锁紧环两端施压来代替螺钉由弯矩产生的轴向力，造成了分析时锁紧环承受的力略大于实际螺钉紧固时锁紧环承受的力。由图4可知，不同U型槽斜边角度下，承载受力区整体所受接触压力差别不大，但在各承载受力段，随着U型槽斜边角度的增加，承载受力区所受的接触压力就越小。对比解析法与有限元法的接触压力值，如表4，两者误差值较小。

图3 U型槽斜边角锁紧环应力云图

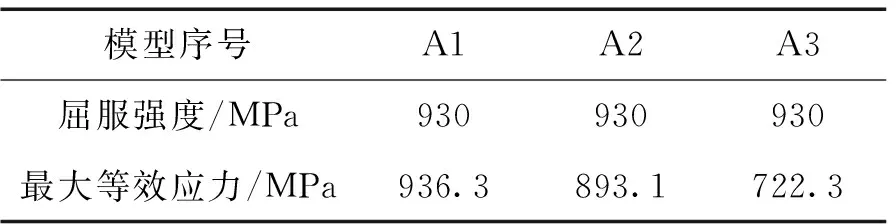
表3 屈服应力与最大等效应力对比表

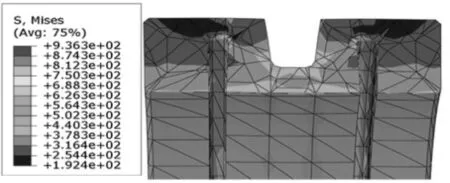
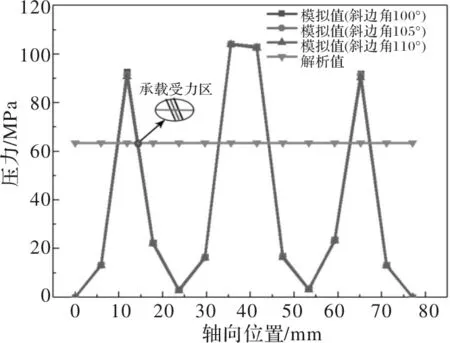
图4 主轴外表面接触压力对比(U型槽斜边角组)

表4 改变锁紧环U型槽斜边角接触压力对比表

综合以上分析，该锁紧环结构是可行的，U型槽斜边角的增加能够减少应力，增加使用寿命。但U型槽斜边角的增加会减少承载受力区的接触压力。实际设计中，为改善应力集中，可考虑在保证承载受力的情况下，设计使用U型槽斜边角较大的结构。

4.2 顶端距/底端距组锁紧环等效应力、接触接触压力分析

仅改变顶端距/底端距，建立不同变量的有限元模型，由图5可知，三个模型的应力分布大致相同，应力集中位置主要分布在U型槽斜边角及内部窄槽处，最大等效应力低于材料的屈服强度。随着顶端距/底端距不断增大，锁紧环最大等效应力逐渐减少，增加顶端距/底端距可以有效的减少应力集中，由图6可知，顶端距/底端距的增加可以减少承载受力区所受接触压力。对比解析法与有限元法接触压力值，如表5，两者误差值相对较小。

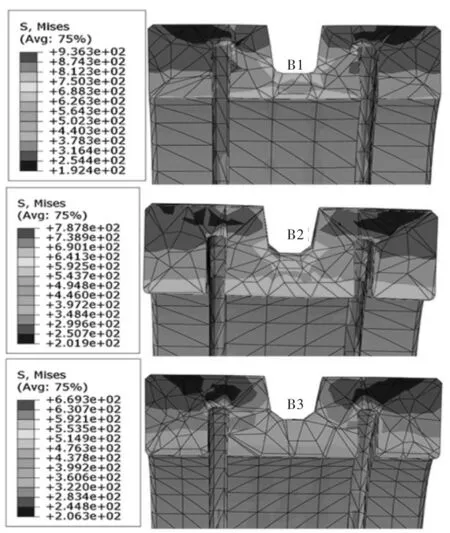
图5 顶端距/底端距组锁紧环应力云图

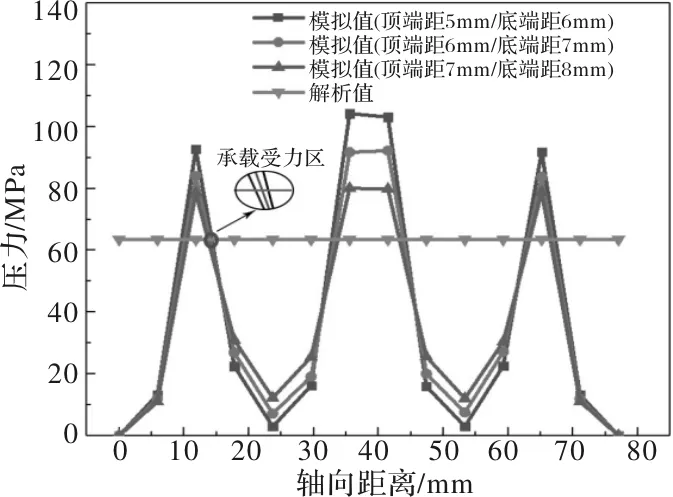
图6 主轴外表面接触压力对比(顶端距/底端距组)

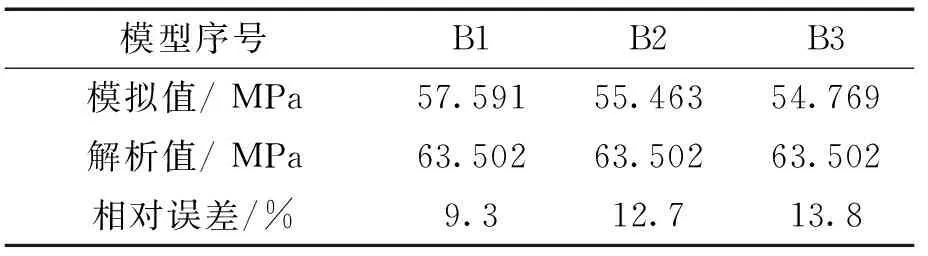
表5 改变锁紧环顶端距/底端距接触压力对比表

综合以上分析，该锁紧环结构是可行的，顶端距/底端距的增加能够有效减少应力，增加锁紧环使用寿命。但是和U型槽斜边角组一样，锁紧环顶端距/底端距的增加会减少承载受力区的接触压力。实际设计中，为改善应力集中，可考虑在保证承载受力的情况下，设计使用顶端距/底端距较大的结构。

4.3 内部窄槽宽度组锁紧环等效应力、接触压力分析

保证锁紧环U型槽斜边角及顶端距/底端距，改变内部窄槽宽度，建立C1、C2、C3三组有限元模型进行分析，由图7可知，与前两组模型一样，应力集中位置主要分布在U型槽斜边角及内部窄槽处。应力分布大致相同，最大等效应力低于材料的屈服强度，随着内部窄槽宽度不断增大，锁紧环的最大等效应力逐渐减少，增加内部窄槽宽度可以有效的减少应力集中，由图8可知，内部窄槽宽度的增加可以提高承载受力区所受接触压力。对比解析法与有限元法的接触压力值，如表6，两者误差值较小。

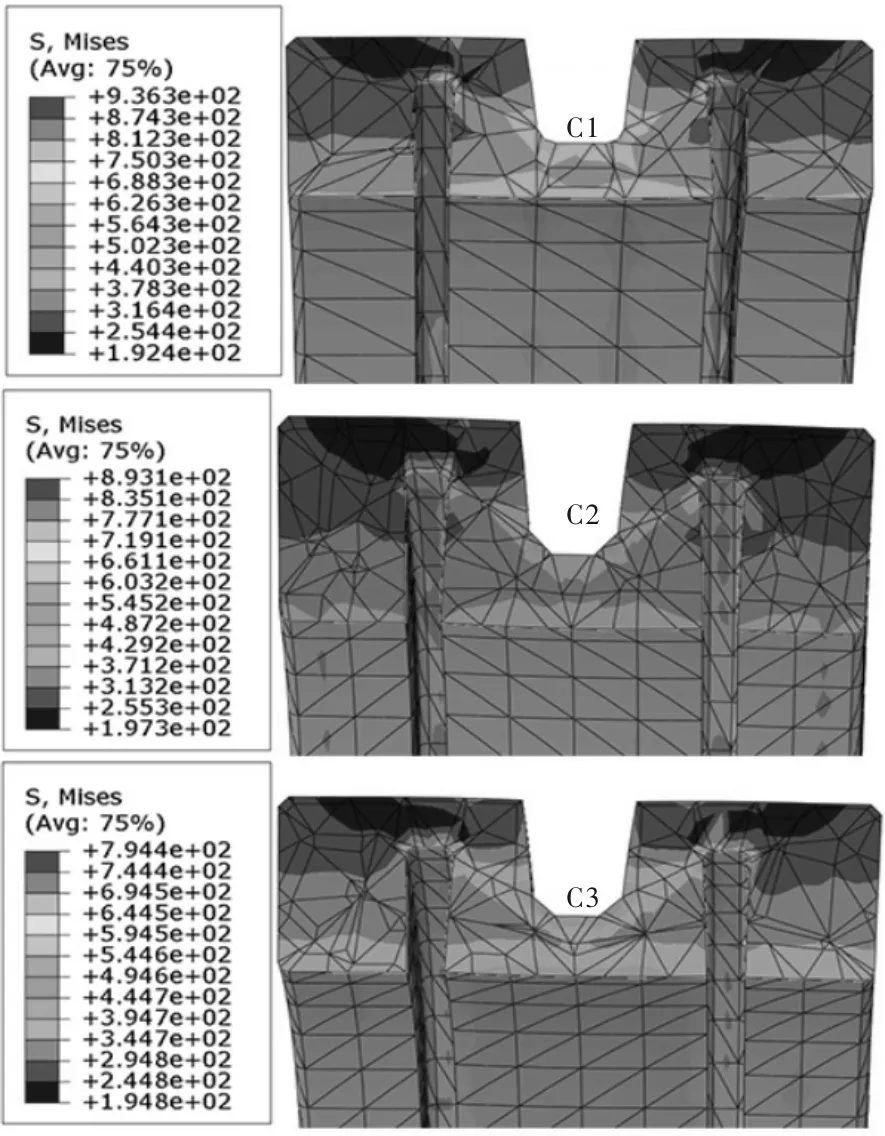
图7 内部窄槽宽度组锁紧环应力云图

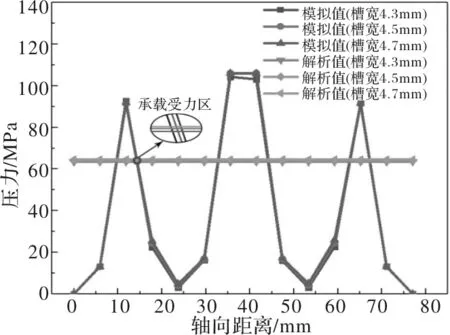
图8 主轴外表面接触压力对比(内部窄槽宽度组)

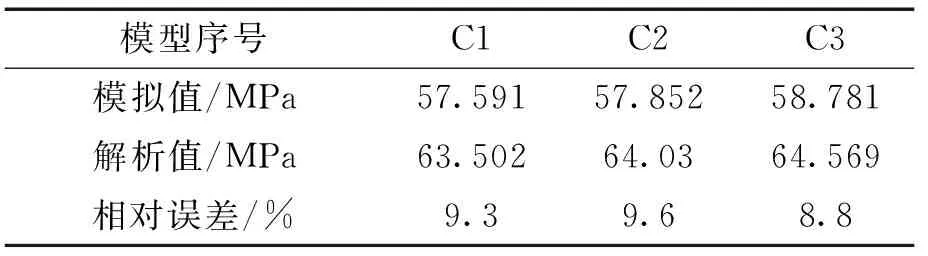
表6 改变锁紧环内部窄槽宽度接触压力对表

综合以上分析，该锁紧环结构是可行的。锁紧环内部窄槽宽度的增加能够减少应力，提高锁紧环使用寿命，增加承载其承载能力。在设计时，应该根据实际情况选择内部窄槽宽度较大的锁紧环结构。

5 结论

(1)提出了一种该类锁紧环计算校核的解析算法，计算了锁紧环配合面接触压力，校核了锁紧环材料屈服强度，并与有限元结果进行对比，验证了该算法的可靠性，为以后该类无键联接锁紧环的设计提供了理论依据。

(2)采用Abaqus软件模拟锁紧环联接装配过程，验证了该结构的可行性，定量分析了应力集中问题，确定了该结构应力集中主要发生位置，为该类锁紧环以后的结构优化提供了一个更为准确的思路，具有一定的工程实用意义。

(3)通过多参数设计分析方法，得到了提高锁紧环承载能力的措施，即：降低锁紧环的U型槽斜边角及顶端距/底端距，增加内部窄槽宽度；另外，可通过适当增加U型槽斜边角、顶端距/底端距及内部窄槽宽度来降低接触应力。

(4)虽然该无键联接锁紧环已通过解析法与数值模拟分析验证了结构可行性，企业也已试产，但是该结构可靠度还需根据其在实际应用中的表现进一步的探究。