矫直板材所需弯曲变形力矩的计算分析

赵 岽

(太原重工股份有限公司矫直机研究所， 山西 太原 030024)

0 前言

辊式板材矫直机是板带车间重要的精整设备，其具有多种结构形式，采用不同的矫直方案，由多个矫直辊对已变形的板材连续施加相应的反弯，使板材经反弯弹复后最终达到平直状态。轧件弯曲变形所需力矩是总矫直力矩的重要组成部分，其在各个矫直辊上的分布受矫直机结构形式和矫直方案不同而存在很大的差异。因此结合不同的矫直条件准确计算弯曲变形力矩，是进一步得出总矫直力矩、校核辊子强度、确定电机功率的重要前提。

1 弯曲变形力矩的总体计算

矫直板材所需的弯曲变形力矩Mb可根据矫直时外力所做功等于轧件产生塑性变形功的条件计算，即

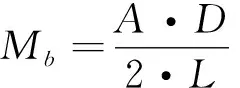
(1)

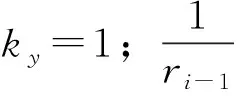
(2)

Mb=Mb2+Mb3+…+Mb(n-1)=

可简化为

当考虑具有双向原始曲率的轧件，凹度向下时弯曲变形力矩较大的情况，可以表示为

(3)

公式(3)只是一个总体计算公式，具体弯曲变形力矩的计算还需结合矫直机的结构形式与矫直方案来进行。

2 弯曲变形力矩的典型分类计算

矫直机的结构形式基本上可分为上下辊倾斜排列、上下辊平行排列两种形式，矫直方案主要可分为大变形和小变形方案，可按此分类对弯曲变形力矩进行计算。

2.1 上下辊倾斜排列结构矫直机的弯曲变形力矩计算

上下辊倾斜排列的矫直机，对宽度为B，厚度为H，弹性模量为E，屈服强度为σs的轧件矫直时，各辊处的总反弯曲率

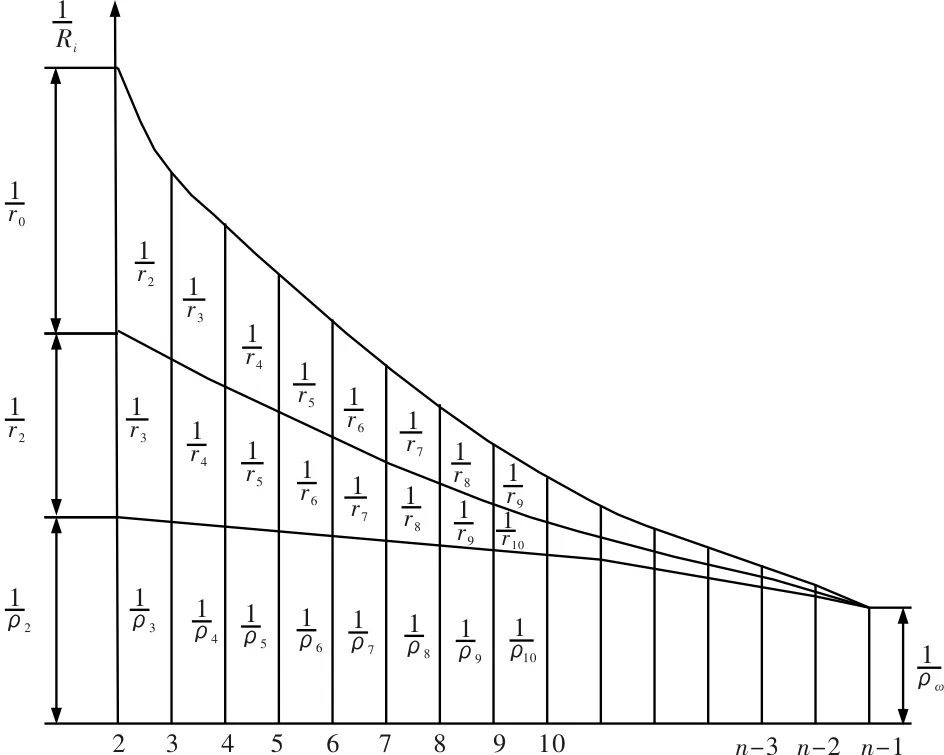
图1 轧件弯曲曲率沿各辊的变化

为简化计算，可近似认为

则

整理得

(4)

公式(4)是一般上下辊倾斜排列结构的弯曲变形力矩计算公式，还可依据金属板材弹塑性弯曲的几何与力学特性，选取具有典型特点的小变形和大变形矫直方案作进一步计算。

2.1.1 小变形矫直方案的弯曲变形力矩计算

该矫直方案设定各辊压下量原则为，应使进入该辊的轧件经反弯和弹复后，轧件的最大曲率能完全消除而矫直。应用小变形方案矫直时，考虑到轧件最大原始曲率都较大，可设定第2辊的反弯曲率至材料的最大弹复曲率

则轧件原始曲率最大部分得到矫直，而原先平直的部分(原始曲率为0的部分)所受反弯最小，弹复能力最弱，成为第2辊处的最小弹复曲率

其残留曲率成为第2辊处的最大残留曲率

整理得上下辊倾斜排列结构小变形矫直方案的弯曲变形力矩计算公式为

(5)

2.1.2 大变形矫直方案的弯曲变形力矩计算

第2辊处最小弹复曲率

第2辊处最大残余曲率

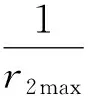
(6)

整理得出上下辊倾斜结构矫直机的弯曲变形力矩计算公式

(7)

(8)

式中，Kn为矫直方案系数；小变形矫直Kn≤1.4；大变形矫直Kn≤2.8；

2.2 上下辊平行排列结构矫直机的弯曲变形力矩计算

对于上下辊平行排列的矫直机，上排各辊都是集体升降的，压下量相同，第2辊和第n-1辊的反弯曲率可由下排两边辊进行调整，因此除第2辊和第n-1辊外，其它各辊的反弯曲率和矫直力矩可以认为是相同的，故弯曲变形力矩可以写为三项之和

分别按小变形与大变形矫直方案设定上排各辊反弯曲率，轧件经若干辊子矫直后，残余曲率趋于定值，通过调整第n辊反弯量使n-1辊的反弯曲率等于弹复曲率时，板材连续通过被完全矫直。上下辊平行排列结构矫直机弯曲变形力矩的计算公式可整理为[1]

(9)

(10)

式中，k1为第2辊变形程度系数，小变形取k1=1.85，大变形取k1=5.82；k2为中间辊变形程度系数；小变形取k2=1.8，大变形取k2=5.76；k3为第n-1辊变形程度系数，小变形取k3=1.05，大变形取k3=1.22。

3 弯曲变形力矩的综合分类计算

矫直机在对不同规格、性能以及弯曲程度的板材进行矫直时，矫直方案的制定不应受小变形和大变形矫直方案的局限，而应结合这两种方案与实践经验综合制定；由于矫直机设备参数固定，矫直方案的应用灵活多样，因此结合设备结构特点，综合板材弯曲变形的几何规律与力学特性，提出假设条件，进而计算弯曲变形力矩。

3.1 上下辊倾斜排列结构矫直机的弯曲变形力矩计算

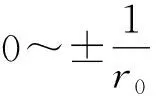
(11)

(12)

3.2 上下辊平行排列结构矫直机的弯曲变形力矩计算

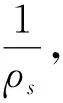
(13)

(14)

4 以各辊对轧件的相对总反弯曲率值Ci计算弯曲变形力矩

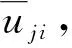
(15)

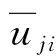
5 上排辊整体倾斜调整矫直方案弯曲变形力矩计算

上排辊整体倾斜调整结构的矫直机属于上下辊倾斜排列结构的特例，特点是各辊压下量呈线性递减分布，在对轧件进行矫直时，加大第2、第3辊的压下量使残余曲率的不均匀性迅速缩小，然后经其余各辊线性递减的压弯弹复后，残余曲率的不均匀性逐步减小趋近于0，进而达到矫直精度要求，此类矫直机具有结构简单，压下参数设置方便快捷的优点，在生产实践中有着广泛的应用。但其对轧件的反弯变形过程复杂，在残余曲率Cc>1的大压弯阶段，压下量所对应的相对反弯曲率是抛物线的，在相对残余曲率Cc<1的小压弯阶段是线性的，残留曲率收敛规律不完全一致[4]，故本文进行单独讨论。

5.1 计算方法一

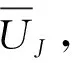
(16)

5.2 计算方法二

(17)

5.3 计算方法三

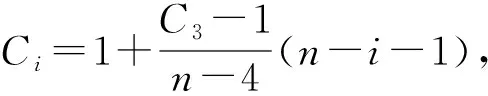
(18)

0.225C3+2.25

(19)

为简化计算，绘制成塑性变形折算系数a计算图，如图2所示，对于单向浪形的轧件C2为4.5～6；对于双向浪形的轧件C2为10，可根据辊数n及C2值直接查得α值。

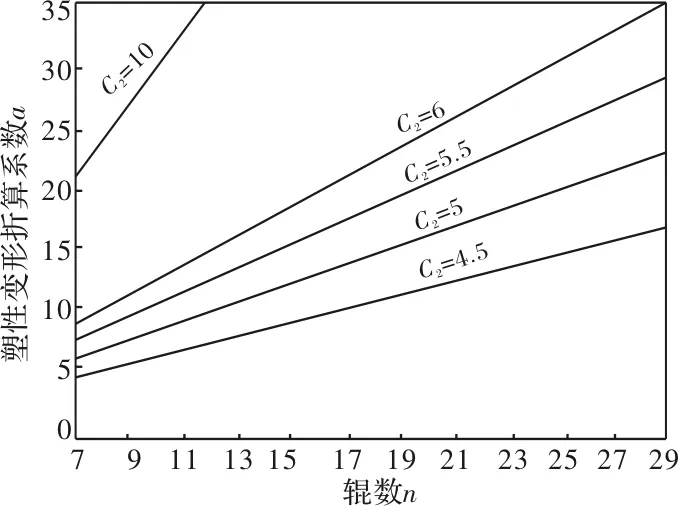
图2 塑性变形折算系数计算图

比较3种计算方法，计算方法一的计算值最大，计算方法二的计算值最小，计算方法三的计算结果接近公式(8)，按大变形矫直方案的计算值。

6 矫直方案与塑性变形折算系数的关系

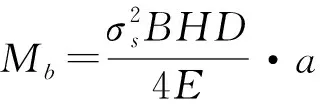
结合设备结构及所应用矫直方案的特点，归纳塑性变形折算系数的分类计算列表，见表2。

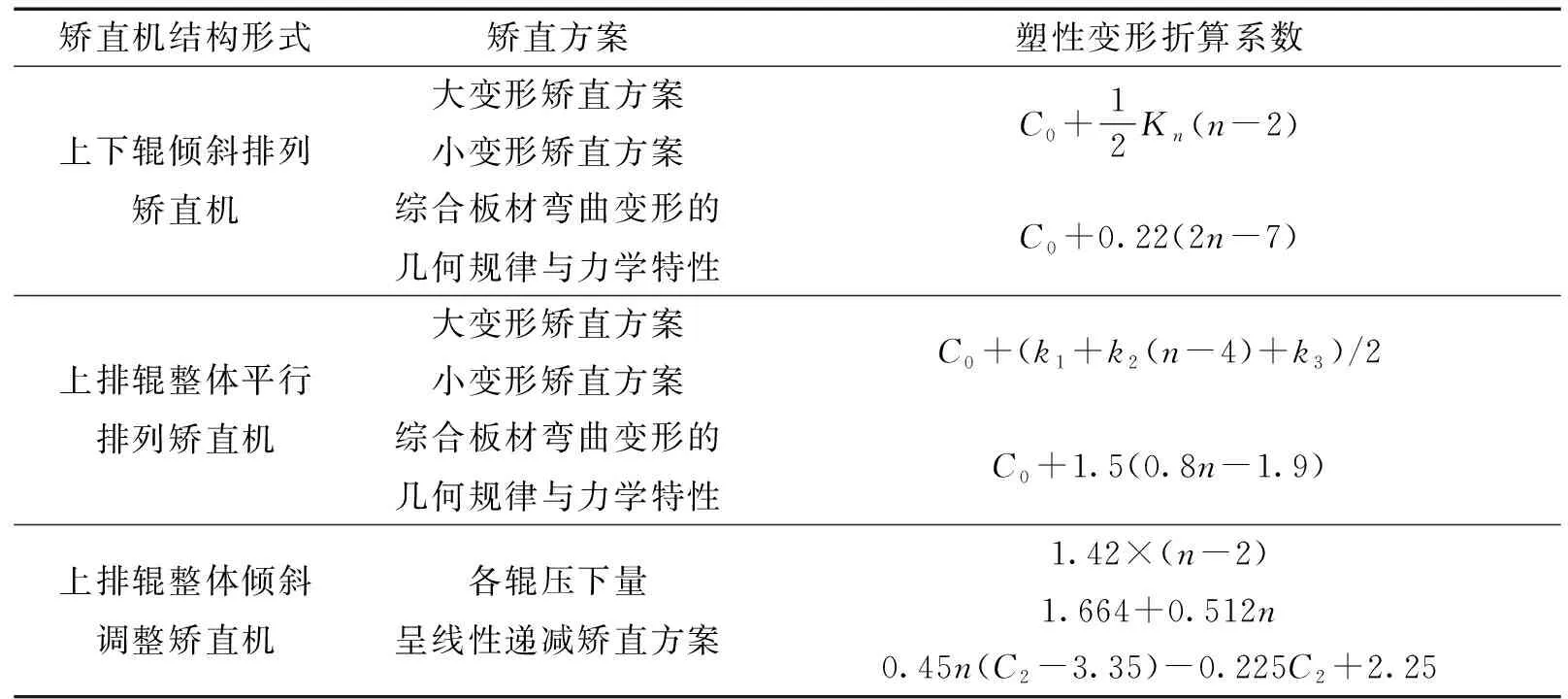
表2 塑性变形折算系数分类计算表

6 结束语

轧件弯曲变形所需力矩是总矫直力矩的主要部分，由于受不同设备结构形式和多种矫直方案的影响，弯曲变形力矩的计算存在方法多样、计算值差异很大的情况。根据矫直原理，针对不同设备结构及所应用的矫直方案进行分析，总结归纳弯曲变形力矩的计算方法，可为弯曲变形力矩的准确计算提供参考，对设计新的矫直机和优化现有矫直机的工艺过程都具有重要的意义。