多尺度形态学的风电轴承故障诊断研究

田 军,李劲涛

(1.吉林电子信息职业技术学院 电气工程学院，吉林 132021 )

0 前言

由于近年来全球温室效应越来越严重，清洁能源的使用受到人们广泛的关注。风能是清洁、无污染的可再生能源之一。随着我国经济快速发展， 国内用电量的增加，我国的风力发电机安装量正在逐年增加。但是由于风力发电机常年服役在野外等复杂的工作环境，这给风机的安全运行维护带来巨大难度。风力发电机的传动系统承受着低速重载的作用，故其传动系统经常发生故障[1-4]。其中因轴承引发的风机事故占总事故的45%。当轴承发生局部故障时，会产生周期振动的冲击信号。轴承的故障特征受到噪声干扰而无法识别，这使轴承的故障诊断非常困难。因此如何从轴承的振动信号里提取有用的故障特征，对风机的安全维护起着至关重要的作用[5-7]。

数学形态学是一种形式简单且计算效率高的数学方法。数学形态学早期被应用在图像处理上，由于其优越的滤波性能，现在被广泛地应用在机械信号的信号处理上[8-11]。数学形态学由四种基本形态学算子组成，每种形态学算子能够对信号产生不同的处理方式。膨胀算子能够扩展波峰，腐蚀算子能够扩展波谷，开算子提取负脉冲，闭算子提取正脉冲。由这四种基本形态学算子可以组合成具有滤波功能的差分算子。传统的形态学采用单尺度处理信号。在处理信号的过程中由于单尺度形态学包含故障信息不完整。因此，本文在单尺度的基础上研究多尺度形态滤波[12-14]。最终， 通过对实际风力发电机的故障信号分析，证明了该方法的有效性。

1 形态学分析

1.1 基本形态学算子

数学形态学主要由 4 种基本形态学算子组成。假设获得的振动信号f(n)其表达形式为F=(0,1,…,n-1)， 结构元素g(m)的表达形式为G=(0,1,…,m-1) (n≥m), 则膨胀、腐蚀、开算子和闭算子分别定义如下：

(f⊕g)(n)=max[f(n-m)+g(m)]

(1)

(fΘg)(n)=min[f(n+m)-g(m)]

(2)

(3)

(f•g)(n)=(f⊕gΘg)(n)

(4)

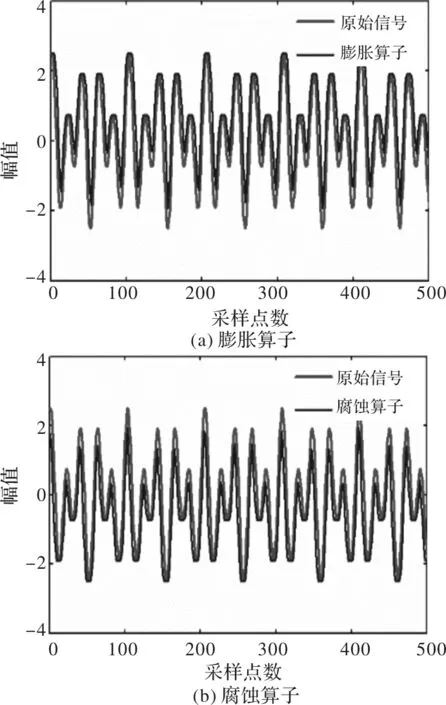
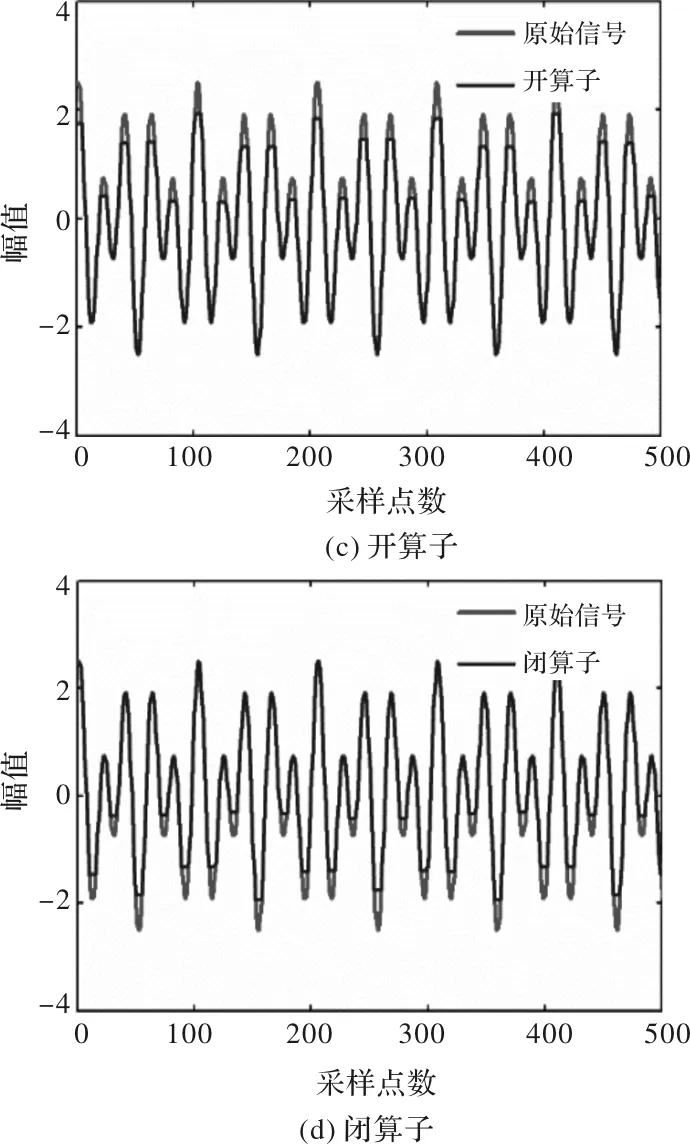
图1 四种基本算子性能

基于4种基本算子构建增强差分算子为EDO。

(5)

1.2 多尺度形态学分析

由于多尺度形态学比单尺度含有较丰富的故障特征信息，因此本文研究多尺度形态学的故障诊断方法。假设ε(ε=1, 2, 3, …,λ)是结构元素SE的尺度，多尺度形态学算子定义如下：

多尺度膨胀算子：

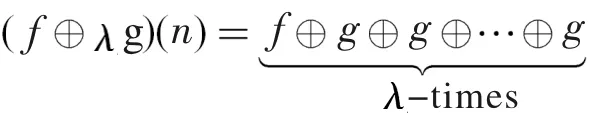
(6)

多尺度腐蚀算子：

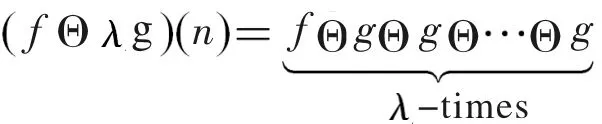
(7)

多尺度开运算：

(8)

多尺度闭运算：

(f•λg)(n)=((f⊕λg)Θλg)(n)

(9)

则EDO算子在多尺度形态下的表达式为

(10)

2 结构元素的尺度选择

2.1 结构元素

结构元素 SE 主要由高度、形状和长度三部分组成。研究表明 SE 的高度和形状对滤波结果影响较小[15]。因此，本文选择高度为零的扁平型结构元素。SE 的长度与尺度的对应关系如表 1 所示。

表1 SE尺度与长度的对应关系

2.2 TEK评价因子

峭度是检测冲击信号的四阶无量纲统计量。其表达式定义如下：

(11)

式中，E()表示数学期望；μ和σ分别表示均值和标准差。

Teager能量算子能够跟踪检测信号的瞬时能量。对于离散信号x(t),其能量算子的表达式为

φ[x(t)]=[x(t)]2-x(t+1)x(t-1)

(12)

Teager 能量算子能够同时考虑信号的瞬时频率和幅值的影响，是一种有效的检测冲击信号的指标。为了最大限度提取冲击信号，本文采用 TEK 指标进行选择。TEK 指标[16]由峭度谱和Teager 能量算子组成，其表达式为

(13)

在通过TEK确定 MEDO 的最优尺度后，把选则的尺度进行加权，输出的最终信号为

(14)

其中，ωλ表示在不同尺度λ下的加权系数。

3 实验验证

本文提出一种风力发电机滚动轴承的故障诊断方法研究，其算法的技术路线如图2所示。

图2 本文算法的技术路线

实验的测试数据来自黑龙江佳木斯的某企业风场。风机的型号为 D70 1.5MW双馈异步发电机。测试时，风的切入速度为3 m/s，切出速度为25 m/s。发电机的转速为1 200 r/min。发电机的额定功率为1 500 kW，实验采用加速度传感器收集振动信号，实验设备的采样频率12 000 Hz。实验测试装置和传感器的安放位置如图3所示。

图3 实验测试装置及传感器安装示意图

通过图3的加速度传感器收集振动信号数据，测试的轴承型号及几何参数如表2所示。通过表2计算得到风机轴承的故障频率分别为： 内圈106.5 Hz, 外圈93.5 Hz, 保持架11.7 Hz, 滚动体190.9 Hz。测得的风机时域图和频域图分别如图4a和图4b所示。

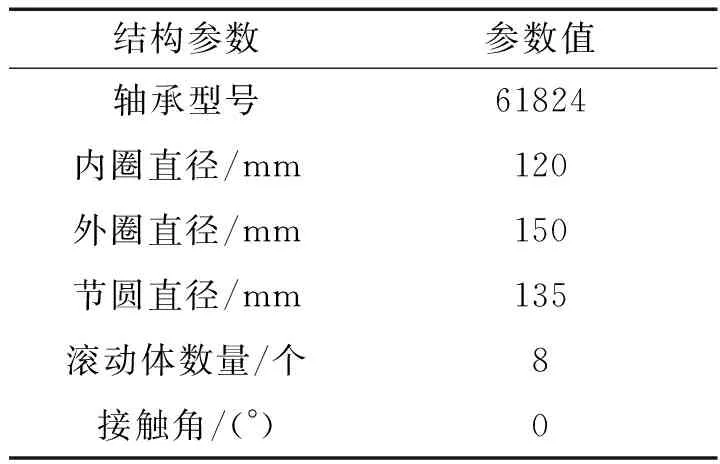
表2 滚动轴承的几何参数

图4 风机实验信号的时域波形与频域波形

在图4b的频谱中无法识别出滚动轴承有效的频率成分，故障特征受背景噪声干扰严重。对实验信号进行包络谱分析，分析结果如图5所示。在图5中可以识别到风机轴承微弱的外圈故障频率106.9 Hz。但是外圈故障频率的幅值较为微弱。

图5 风机实验信号的包络谱

采用本文提出的方法对实验信号进一步处理。首先应用MEDO处理实验信号，得到的多尺度时域图和多尺度频域图分别如图6a和6b所示。从图6b中可以发现，不同尺度下经MEDO方法处理的结果不同，尺度越小故障信息越完整但是噪声越多，相反尺度越大噪声越小但是故障信息不完整。因此如何选择最优尺度对MEDO方法影响巨大。

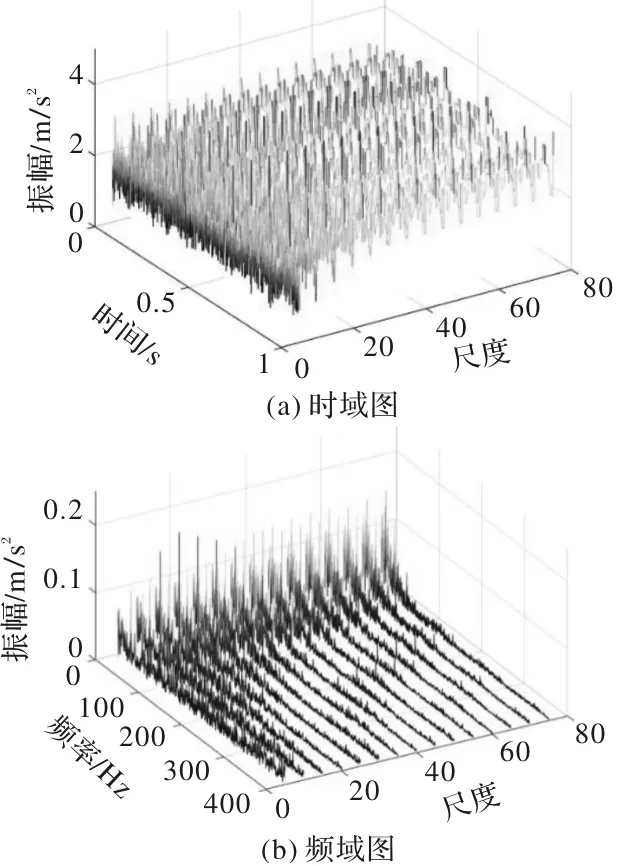
图6 实验信号在多尺度下的时域图和频域图

采用TEK衡量指标去选择MEDO的最优尺度，得到的TEK优化曲线和在最优尺度下最终获得的加权结果分别如图7a和7b所示。在7a中可以发现当尺度为21的时候，TEK值最大。因此MEDO的尺度加权范围为1到21。在图7b中，轴承外圈的故障频率106.9 Hz、213.8 Hz以及三倍故障频率320.7 Hz能够清楚的被看到。并且轴承的2倍转频40 Hz也能清楚的看到。对比图5和图4b，本文提出的算法能够更有效的识别出风机轴承的故障特征频率。

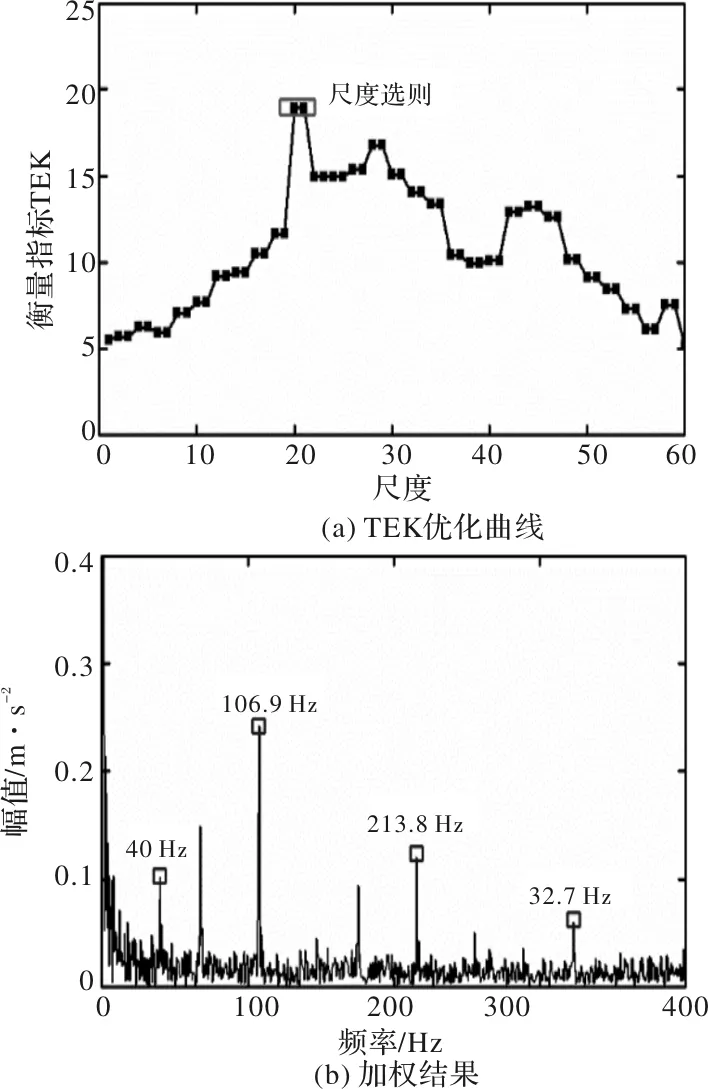
图7 MEDO方法处理实验信号结果

为了进一步证明本文提出方法的优越性，采用单尺度的EDO方法和EEMD方法[17]处理相同的实验信号。处理结果分别如图8和图9所示。在图8中，EDO方法处理实验信号只能看到故障频率106.9 Hz和213.8 Hz。但是从图中可以看到213.8 Hz的轴承故障频率受噪声干扰严重。在图9b中可以看到，经EEMD方法处理后可以识别出106.9 Hz和213.8 Hz的轴承故障频率。但是其故障幅值依然比较微弱。这两种方法与本文提出MEDO方法进行对比，可以进一步表明本文提出算法的优越性。

图8 EDO 方法处理实验信号的结果

图9 EEMD方法处理实验信号的结果

4 结论

为了检测大型风力发电机滚动轴承的微弱故障，一种多尺度的MEDO形态学分析方法被提出。通过对风机实验信号的检测结果可以发现。FFT谱和包络谱无法准确的识别出轴承故障。而MEDO方法可以有效地检测出轴承外圈故障频率106.9 Hz、213.8 Hz以及三倍故障频率320.7 Hz。与EDO方法和EEMD方法的实验对比结果表明，本文提出的方法具有优越的滚动轴承故障特征提取能力。