空间绳网旋转展开动力学分析
秦志伟,刘 振,孙国鹏,祁玉峰
(1. 哈尔滨工业大学机械工程系,哈尔滨 150001;2. 北京空间飞行器总体设计部,北京 100094)
0 引 言
随着人类对太空的探索,大量卫星被送入太空,这个过程累积的抛弃物、火箭爆炸物等严重污染着太空环境,已经失效的卫星或碎片相互撞击又将产生更多的碎片,这些碎片的平均轨道速度为7 km/s至13 km/s,与航天器的平均撞击速度达10 km/s,一旦发生撞击事故,将导致航天器损毁,是空间在轨卫星、空间站严重的潜在威胁[1-2]。因此,针对空间碎片的主动捕获及销毁技术的研究尤为重要[3]。而绳网捕获相比于对接式抓捕和机械臂抓捕等刚性捕获方式具有收拢空间少、误差冗余大、安全性高等优点,在非合作特征显著的空间废弃卫星等抓捕中有着重要的应用需求[4]。
鉴于此,2001年,欧空局(ESA)提出了用于抓捕地球静止轨道废弃卫星,并将其转移到坟墓轨道的ROGER计划[5]。2018年9月,英国萨里航天中心(SSC)首次通过卫星直接弹射储存舱内的绳网进行了捕获空间碎片的在轨实验[6],验证了空间绳网捕获方式的可行性。瑞典皇家理工学院(RIT) Gärdsback等应用商业软件MATLAB和LS-DYNA对基于中心毂轮旋转展开的绳网模型进行了无控展开和受控展开的动力学研究[7-8]。瑞士斯德哥尔摩皇家理工学院(KTH)进行了名为“Suaineadh”的太空测试实验以验证该类旋转展开方案[9]。国内对于空间绳网展开的研究起步较晚,但也进行了许多有益的探索。北京航空航天大学赵国伟等[10]基于商业软件LS-DYNA对网体展开过程中的绳体材料的拉伸和回复过程进行了数值模拟。哈尔滨工业大学张越等[11]设计了一种四角质量块发射角度可调的“弹抛式”捕网发射系统,增加了发射的可靠性。国防科学技术大学张青斌等[12]对绳网系统展开动力学特性进行了天地差异性分析,通过与地面实验的校验来反推太空环境下绳网展开的运动状态;文献[13-14]设计了一种空间飞网的二级发射展开方式,增加了网体抛出的可靠性;陈青全等[15]采用定力撕裂带对绳网网型进行了控制研究。文献[16-17]基于商业软件ABAQUS和自编程序THUsolver对直接弹射抛出的网体展开过程进行了参数分析和优化。文献[18-19]针对空间绳网捕获系统建立了收口阶段质量块的动力学模型,并对绳网系统的收口机构进行了设计和优化。
对上述文献进行分析发现,文献[4,10-17]采用直接抛射网体展开方案,火工装置发射时存在对发射平台冲击大、展开后绳网网型维持时间短等问题;文献[7-9]为基于中心毂轮旋转展开方案的分析和实验,实现该方案的控制过程复杂且难以保证展开的有效性;文献[18-19]提出的收口形式可作为绳网展开后实现收口作业系统设计的重要参考。本文提出了一种基于周置可控旋筒的旋转展开空间绳网系统方案;利用拉格朗日动力学方程构建了网臂解析模型,采用MATLAB、ABAQUS软件构建了网臂/网体有限元仿真模型并进行了模型间的仿真对比校验;最后基于网体有限元仿真模型对绳网网型、旋筒控制策略进行了优化分析。
1 空间绳网系统的旋转展开方案
本文提出的基于周置可控旋筒旋转展开的网体卷绕方案如图1所示,图1(a)~图1(d)为网体的折拢过程。与文献[7]中基于中心毂轮旋转展开方案的折叠过程类似,正方形的空间网体沿四边中心线呈“N字形”聚拢到绳网中心形成空间网臂,为保证网体有序展开,折拢过程中网体外边始终在最外侧。将四个网臂分别按顺时针(逆时针)卷绕在四个旋筒上,限制四个旋筒的相对位置实现网体的预先收拢,如图1(e)~图1(f)所示。

图1 网体折叠和卷绕过程Fig.1 Space web folding and rolling sequence
空间绳网系统的旋转展开过程可视为上述卷绕过程的逆过程,空间绳网实现捕获操作的具体过程如下:
1) 起旋阶段,旋筒及缠绕其上的网体以相同的角速度旋转。
2) 释放阶段,将旋转状态的空间绳网系统以一定初速度弹出。
3) 解锁阶段,绳网系统弹出后经预设时间后,限位机构解锁,同时旋筒内的控制系统启动,四个旋筒此时具有相同大小的角速度和平动速度。
4) 展开阶段,四个旋筒带动缠绕其上的网体有序展开并维持一定时间。
5) 捕获阶段,当网体包覆非合作目标后,收口机构实现网体收口。
2 空间绳网系统的模型构建
卷绕收拢的网体在旋转展开过程中,相同时刻下网体不同区域的质量和速度难以直接描述,构建网体解析模型较为困难,但由文献[7-8,10,16-17]可知,有限元仿真是模拟绳网展开动力学过程的有效手段。因此,本节首先构建出具有相同工作过程的网臂解析模型;在ABAQUS/Explicit仿真环境下,通过对网体折拢后中心约束区域自由度的不同定义构建出网臂/网体旋转展开有限元仿真模型(见图2,网臂有限元仿真模型的中心区域绑定约束,网体有限元仿真模型中心区域无约束),对比分析上述三种模型以检验有限元仿真模型的有效性。

图2 网臂模型与网体模型的关系Fig.2 The relationship between arms and webs
2.1 基于拉格朗日动力学方程的网臂解析模型
网臂解析模型构建的假设如下:
(1) 四个旋筒视为理想匀质筒状壳体。
(2) 网臂视为有质量、无厚度的直线。
(3) 网臂的线密度从绳网中心到外侧与旋筒的固定端线性减小。
(4) 旋筒和网臂始终在垂直于旋转轴的平面内运动,忽略网臂在展开平面外的波动。
(5) 忽略网臂与自身的内摩擦、网臂与旋筒间的摩擦耗能。
(6) 四个旋筒及卷绕在其上的网臂在展开过程中呈中心对称状态。
根据假设(6),取其中一条网臂进行分析。选择旋筒转角θ和网臂卷绕角φ作为系统的广义坐标,建立如图3所示的动力学分析模型,其中固定坐标系为O0-x0y0z0、平动坐标系为O1-x1y1z1、网臂旋出切点处的动坐标系为O2-x2y2z2。以R和r表示旋筒的几何中心相对于定坐标系O0-x0y0z0和动坐标系O2-x2y2z2的位置矢量,L表示动坐标系原点O2相对于定坐标系原点O0的位置矢量。

图3 旋转展开分析模型Fig.3 The analytical model based on rotation
根据矢量关系
R=L+r
(1)
对式(1)等号两边求导可得

(2)
根据假设(1),四周旋筒相对于各自旋转轴的转动惯量J为
J=mhr2
(3)
式中:mh为旋筒质量,r为旋筒半径。
根据网臂的展开方式,网臂的旋出长度L为
L=Lmax-rφ
(4)
(5)
式中:S为绳网边长,Lmax为网臂旋出的最大长度。
根据假设(3),网臂上任意绳段微元dm处的线密度ρl为
(6)
式中:mw为绳网质量,n为旋筒个数,l为任意绳段微元dm与动坐标系原点O2间的距离。
系统总动能EK由仍卷绕在旋筒上的网臂的动能EK1、已经旋出的网臂的动能EK2、旋筒的动能EK3三部分组成,整理为
(7)
由总动能列写第二类拉格朗日方程
(8)
其中,
(9)
式中:Ff为作用在四个旋筒上的控制力矩之和。
(10)
2.2 基于中心差分算法的有限元仿真模型(FEM)
本文采用ABAQUS/Explicit构建绳网有限元模型,仿真模型的建立过程如下:
1) 根据网体初始折叠方式(见图1),通过MATLAB软件编程输出绳网部件中单元的节点连接关系和节点的三维坐标,直接构建出绳网部件的网格模型。绳索单元的节点连接关系可由网目内单元分段数(a)、绳网网目数(b)描述,如图4所示。

图4 绳网仿真模型节点序号排布定义Fig.4 The arrangement of nodes in the FE web models
2) 将预先定义的正交叉状的折叠绳网模型导入ABAQUS/CAE界面中,采用壳单元创建旋筒部件,旋转平移四周旋筒,使绳网紧密卷绕在四个旋筒上,得到初始装配误差很小的装配体(误差来源于软件的接触识别精度),构建过程如图5所示。

图5 系统装配模型的构建过程Fig.5 The construction process of the assembly model
3) 通过导入*odb的方式输出上述装配关系,重新设置材料属性、接触关系、约束条件、预定义场(初速度)等仿真条件,输出inp文件。
4) 采用FORTRAN语言编写VUAMP子程序,实现对旋筒控制力矩的加载。
5) 提交inp文件和子程序进入求解器进行网臂/网体旋转展开动力学分析,软件基于中心差分算法求解动力学平衡方程[16]:
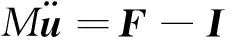
(11)
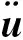
2.3 解析模型与有限元模型的仿真对比分析
本文算例的仿真参数如表1所示。

表1 系统仿真参数Table 1 Simulation parameters of system
采用电机-反作用飞轮的机构实现方式进行控制,控制律初选为
(12)

选取旋筒角速度和网臂旋出长度作为模型间对比的特征变量,旋筒角速度表征网臂/网体及作用在旋筒上的控制力矩对旋筒的影响,有效的控制使网臂/网体展开后角速度在零值附近;旋出长度评价网臂/网体的展开程度,旋出长度越大,展开越充分(为统一对比,绳网模型中旋出长度的定义与网臂模型相同)。通过对网臂解析模型的预先仿真计算得出,当T=267 N·mm时,网臂可完全展开并实现有效的控制,将该幅值引入网臂/网体有限元仿真模型中,得到的展开过程如图6、图7所示。
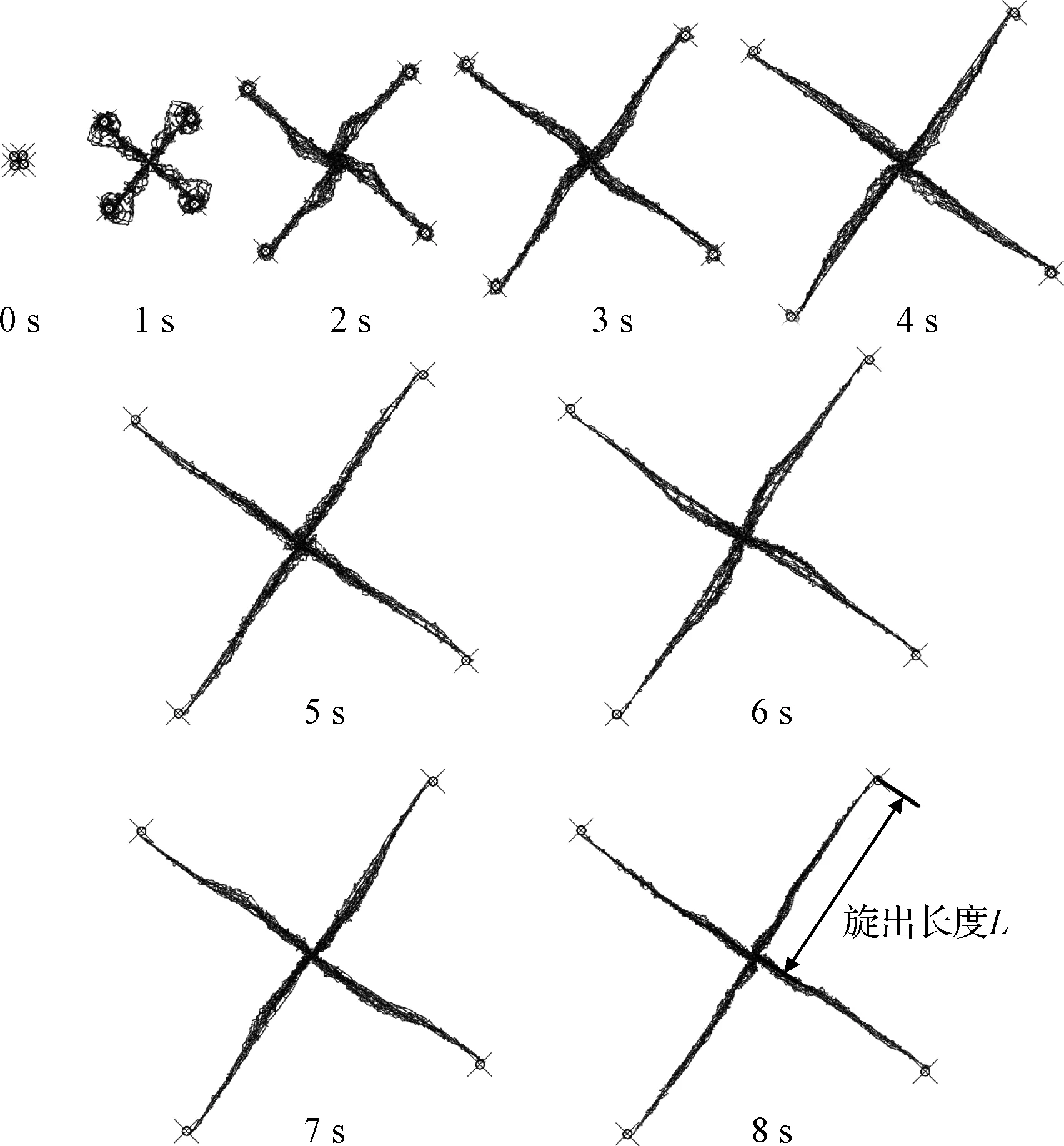
图6 控制力矩作用下网臂展开过程(等比缩放)Fig.6 Controlled deployment of arms (proportional scaling)

图7 控制力矩作用下网体展开过程(等比缩放)Fig.7 Controlled deployment of webs (proportional scaling)
由图8、图9可知,在控制力矩作用下,网臂解析模型和网臂有限元仿真模型的旋筒角速度、网臂旋出长度具有高度的一致性,对比验证了有限元仿真模型的有效性。将网臂有限元仿真模型中心约束取消变为网体有限元仿真模型后,由于两个模型在展开过程中的旋筒最大位移半径和绳网部件内部传力形式的不同,致使两个有限元仿真模型的旋筒角速度和网臂旋出长度存在差异。

图8 控制力矩作用下的旋筒角速度Fig.8 The angular velocity of the rotary tubes under control

图9 控制力矩作用下的网臂旋出长度Fig.9 The length of the arms under control
3 空间绳网网型及展开控制策略优化分析
3.1 空间绳网网型优化
在绳网旋转展开过程中,定义每条网边中心点连接形成的正方形区域为有效捕获区域,其面积即为有效捕获面积;绳网其余边角部分为无效捕获区域,该区域无法对非合作目标进行有效拦截捕获。考虑到实际操作中绳网与旋筒间的绑定连接以及网体在展开过程中有效捕获区域的维持,设计如图10所示的五种网型备选方案(图中为旋转展开过程中的绳网网型状态)。方案一在绳网四角各延伸一截绳段,方便旋筒与网体的绑定连接;方案二至方案五为在方案一基础上增加四种系绳牵拉传力方式。五种方案所用网体边长均为10.4 m,周置旋筒以相同的初始角速度(12.56 rad·s-1)共同旋出且保持该角速度匀速旋转。

图10 绳网网型优化方案Fig.10 The optimization of the web topology
图11为在上述过程中,不同方案下的有效捕获面积对比曲线。在绳网展开初期(0 s~3 s),五种构型方案下的有效捕获面积变化没有明显差别;而在展开后期(3 s~5 s),构型方案三在展开过程中的有效捕获面积维持较高且波动幅值变化最小,故以下研究均在构型方案三的基础上展开。

图11 不同方案下的有效捕获面积对比Fig.11 Comparison of effective capture area in different cases
3.2 绳网系统旋转展开控制策略优化
在仿真模型中引入控制律(12)进行分析,当控制力矩幅值T=220 N·mm时,绳网刚好完全展开且实现了有效的控制(绳网展开后旋筒角速度为零),控制力矩加载曲线如图12所示。绳网尚未完全展开时,电机的输出控制力矩为定值;绳网完全展开后,控制力矩呈频繁的正负往复波动状态。力矩的频繁波动表明此阶段控制力矩幅值设置的不合理,因这种控制状态较为耗能,为此设计了三种分步加载控制策略。

图12 控制力矩波动变化Fig.12 The fluctuations of control torque
策略一为当角速度尚未衰减至零时,以一恒定力矩T控制,当传感器监测到旋筒角速度衰减到零后,电机控制力矩置为零,控制律如式(13)所示。
策略二为当角速度尚未衰减至零时,以一恒定力矩T控制,当旋筒角速度首次衰减到零后,改用一个较小的控制力矩T1控制,控制律如式(14)所示。
(13)
(14)
策略三为当旋筒角速度尚未衰减至零时(定义状态标记为Δ=1),采用较大控制力矩T控制,当旋筒角速度首次衰减到零后(定义状态标记为Δ=2),电机的输出力矩在较小的范围内(-T1,0)波动控制,控制律如式(15)所示。
(15)
采用上述三种分步加载控制策略修正式(12),得到控制力矩的加载情况如图13所示,有效捕获面积的变化曲线如图14所示。比较有效捕获面积的控制效果,策略一的控制效果较差,策略二和策略三的控制效果与原方案大致相同,但却有效地减少了控制力矩的波动幅度和频率。

图13 三种加载控制策略Fig.13 Three loading strategies for controlling torque

图14 不同控制策略下的有效捕获面积Fig.14 Effective capture area under different control strategies
因策略二形式上的简单性,若能通过实验寻找到第二步控制力矩加载的时间和幅值,则可直接采用计时器代替基于旋筒角速度的力矩控制,避免了传感器的引用,降低了控制成本和实现难度。绳网系统在策略二控制下的展开过程如图15所示,选取旋筒中心和网边中心为参考点,两参考点距网体中心的距离半径变化如图16所示。

图15 构型优化后的受控展开(等比缩放)Fig.15 Controlled deployment of the structural webs after optimized (proportional scaling)

图16 参考点与网心的距离Fig.16 The distance between reference points and web center
在旋筒与网体边沿间系绳的牵拉传力作用下,边心与网心的距离在5 s左右达到峰值,此时亦为有效捕获面积的峰值;随着旋筒继续外旋,系绳牵拉绑定结构使边心-网心距具有较小的波动幅度;由于旋筒在绳网完全展开时仍有少量残余平动动能,当旋筒-网心距离达到峰值时,边心-网心距同样出现第二次小高峰,之后网体“回弹”,两参考点距网体中心的距离缓慢减少。
定义有效捕获面积达最大展开面积的60%时,可适用于捕获任务[15];绳网从初始解锁释放到展开达最大展开面积的60%时所用的时间为展开时间,适用于捕获任务的时间为捕获时间。将本文算例的仿真结论与文献[12,15-16]中采用“直接弹抛”展开形式的仿真结论(由绳网展开曲线获得)对比汇总如表2所示,采用本文的旋转展开方案,绳网展开时间相对较慢,但却有效地减缓了网体的“回弹”过程,捕获时间大幅增加,提升了捕获性能。

表2 不同算例的结论对比Table 2 Comparison of conclusions of different samples
4 结 论
本文提出了一种基于周置可控旋筒的旋转展开空间绳网系统方案,采用拉格朗日动力学解析模型和基于中心差分算法的有限元仿真模型对绳网展开过程的动力学特性进行了对比分析,旋筒的角速度、网臂的旋出长度在不同模型的求解下均表现良好的一致性,说明了有限元模型的有效性。
对绳网网型和旋转展开控制策略的优化分析表明:采用系绳同时牵引网体四角及网边中心的构型(方案三)时,绳网在旋转展开过程中有效捕获面积的波动幅度最小;采用分步加载的控制策略,在有效减小控制力矩的波动幅度和频率的基础上进一步确定便于工程实现的旋筒控制策略(策略二);相较采用“直接弹抛”形式展开空间绳网,基于周置可控旋筒的旋转展开实现了更长时间的空间保形。

