动力冗余液体捆绑火箭的POGO稳定性分析
王 涛,容 易,胡久辉,唐 冶,丁 千
(1. 天津大学机械工程学院,天津 300072;2. 北京宇航系统工程研究所,北京 100076)
0 引 言
通过推进系统与箭体结构系统的相互耦合,使液体火箭产生的纵向低频自激振动称为POGO振动[1-3]。POGO振动可能发生在飞行过程中的任意时刻,对运载器的安全性和液体火箭发射可靠性造成严重威胁,对于载人火箭甚至危及宇航员的生命安全,国内外均展开了大量研究。Rubin[4]提出了液体火箭POGO振动的频域分析法,并成功应用此方法分析了大力神Ⅱ运载火箭POGO振动问题。徐得元等[5]利用有理多项式对POGO振动系统中扰动力的传递函数逼近,简化了文献[4]所建立的频域模型。刘涛等[6]基于频域分析法建立火箭POGO振动系统的传递函数。采用矢量拟合法对传递函数进行有理分式拟合,借助极点分布图确定了蓄压器能量值对POGO稳定性的影响。文献[7]应用频域法分析捆绑火箭的POGO稳定性,将推进系统简化为多个独立的单推进剂-单发动机系统。以上是利用频域分析方法,研究液体火箭POGO稳定性问题。而时域方法也受到了众多学者们的关注,Oppenheim和Rubin[8]从时域的角度提出了适用于任何液体火箭POGO振动系统的建模方法,给出了贮箱、推进剂管路系统、泵、蓄压器和推力室等推进单元的建模过程,通过组装单元动力学方程,建立液体火箭推进系统的扰动方程组和结构的纵向振动方程组。Zhao等[9]利用Rubin建模方法和Hurwitz稳定性判据导出单推进剂-单发动机火箭模型的POGO稳定条件,发现推进和结构系统的耦合强度直接影响液体火箭POGO稳定性。谭述君等[10-11]讨论了临界耦合强度理论和临界阻尼比法在POGO稳定性分析中适应性问题,分析结果表明耦合强度是液体火箭是否发生POGO振动的决定因素。唐冶等[12]基于Rubin法和区间数学理论分析了推进系统频率特性的灵敏度问题。Tang等[13]考虑氧化剂和燃料推进系统耦合的影响,利用Rubin法建立了液体火箭POGO振动系统的等效线性化动力学模型。采用Routh-Hurwitz判据,分析了推进系统参数对液体火箭POGO稳定性的影响。张青松和张兵[14]利用键合图理论的思想,解决了Rubin模型的奇异性问题,提出新的液体火箭POGO稳定性分析的状态空间模型,通过仿真证明了该模型的有效性和实用性。Wang等[15]基于独立重量位移描述方法,将Rubin模型中的八种物理单元重新组合,提出了九种独立单元,根据相同节点的脉动压强相等为连接条件,建立微分方程形式的改进Rubin模型,该模型具有维数低和非奇异的优点。王庆伟等[16]利用改进的Rubin建模方法和混合坐标法建立了火箭姿态运动和POGO振动相互耦合的动力学模型,并进一步分析了泵增益和蓄压器能量值对耦合系统稳定性的影响。文献[17]基于改进Rubin方法和模态分解法对推进系统中的输送管路动力学模型降维处理,提出了POGO振动系统时域模型的降维方法。
动力冗余技术[18]指运载火箭在一台或数台发动机出现故障的情况下,自动检测、判别后发出指令关闭此发动机,实时切换或在线重构各分系统控制策略,能提高火箭飞行过程中的推进系统可靠性。大部分情况下,应用动力冗余技术可避免因发动机故障引起发射任务的失败。但对于液体捆绑火箭而言,发动机故障[19-21]不仅会造成推力下降还会引起芯级和助推贮箱内推进剂消耗不均、火箭质心偏移、浪费运载能力等后果,这些问题的解决依赖于交叉输送技术的应用。法尔肯9重型的早期方案采用该项技术保证助推和芯级推进剂按比例平稳消耗。航天飞机V-2通过应用交叉输送技术确保助推器分离时轨道器贮箱仍处于满箱状态,有效提高了运载能力[22]。但在国内,具有交叉输送能力的动力冗余火箭尚处于设计阶段,仅有关于交叉输送管路总体参数和方案设计的研究成果[23-24]。
本文针对推进剂的交叉输送为动力冗余液体捆绑火箭POGO稳定性分析提出了新的任务,以独立工作、一台助推发动机故障助推贮箱向芯级发动机供给推进剂和两助推器同时向芯级发动机供给推进剂三种工作模式为研究对象,利用改进Rubin建模方法[15]建立了液体捆绑火箭POGO振动系统的分析模型,分析了助推器和芯级的蓄压器能量值、泵柔度和泵增益参数对不同工作模式下液体捆绑火箭POGO稳定性的影响。
1 液体捆绑火箭的POGO振动系统
具有交叉输送功能的动力冗余液体捆绑火箭,可通过控制管路阀门的开闭,使推进系统根据实际情况在三种不同工作模式之间相互切换:独立工作(Mode 1),一台助推发动机故障助推贮箱向芯级发动机供给推进剂(Mode 2)、两助推器同时向芯级发动机供给推进剂(Mode 3)。其中Mode 1模式下推进系统交叉输送管路处于关闭状态,每台发动机由独立的氧路和燃路系统供给推进剂。Mode 2模式下发生故障的助推火箭与芯级火箭推进系统通过交叉输送管路相互连通,存在耦合效应。Mode 3模式下芯级贮箱内的燃料和氧化剂不再消耗,各台发动机所需的推进剂由助推贮箱供给。图1为三种工作模式下动力冗余液体捆绑火箭的力学简图。

图1 三种工作模式下动力冗余液体捆绑火箭Fig.1 The liquid strap-on launch vehicle with redundant propulsion system under three different working modes
基于改进Rubin建模方法,本文建立三种工作模式下(Mode 1, Mode 2, Mode 3)具有冗余能力的液体捆绑火箭POGO稳定性分析模型。改进的Rubin建模方法分为三步:1)通过有限元技术建立推进系统的动力学方程组;2)建立箭体结构纵向振动系统的模态方程;3)联立推进系统和箭体结构系统的动力学模型,建立耦合系统的POGO稳定性分析模型。
1.1 推进系统动力学模型
根据改进Rubin建模方法中独立单元的定义,对三种工作模式下动力冗余液体捆绑火箭推进系统进行了单元划分,并依据以下两个划分原则((1)纵向管路划分精细,横向管路划分粗糙;(2)忽略不可压缩管、三通和弯头的长度)得到十二种独立单元:可压缩管、单出口贮箱、推力室、波纹管-可压缩管、可压缩管-波纹管、三通-可压缩管(单入口双出口)、三通-蓄压器、泵-不可压缩管、双出口贮箱、四出口贮箱、三通-可压缩管(双入口单出口)和弯头-可压缩管。其中八种独立单元(可压缩管、单出口贮箱、推力室、波纹管-可压缩管、可压缩管-波纹管、三通-可压缩管(单入口双出口)、三通-蓄压器和泵-不可压缩管)的动力学模型已由Wang等[15]给出,其余四种独立单元的建模过程如下。
1)双出口贮箱
双出口贮箱共有两个节点(见图2(a)),t1和t2,这两个节点均为推进剂流出节点。

图2 几种推进系统独立单元Fig.2 The schematic diagrams of partial independent unit
(1)动力学方程
假设贮箱内的液体冻结在单元中,应用牛顿定律建立其动力学方程为
(1)
式中:pt1,pt2分别为节点t1和t2的脉动压强;Itt,Rtt为双出口贮箱的惯性和阻尼;wtta和wtt表示双出口贮箱内推进剂的绝对脉动重量位移和相对脉动重量位移,它们之间具有如下关系[8]
wtta=wtt+ρgAttNtt·rtte
(2)
式中:ρ,g为推进剂的密度和标准重力加速度;Att和Ntt分别表示双出口贮箱出口的面积和方向向量;rtte为双出口贮箱的位移矢径。由于贮箱含有两个出口,式(2)中的部分变量也可表示为
(3)
式中:wt1,At1,Nt1,wt2,At2和Nt2分别为t1和t2节点的相对脉动重量位移,截面积和方向向量。将式(2)和式(3)代入式(1)可得
(4)
式中:Htt为双出口贮箱的水头矢量,可表示为
Htt=(Nt1+Nt2)Ltt
(5)
式中:Ltt表示贮箱内液体的高度。
(2)双出口贮箱对结构的作用力
多出口贮箱对结构的作用力等于每个出口作用力的叠加。单出口贮箱对结构的作用力可表示为[8]
(6)
双出口贮箱对结构的作用力为
(7)
将式(4)代入式(7)可得
(8)
2)四出口贮箱
四出口贮箱的四个节点(见图2(b),f1,f2,f3和f4)均为推进剂流出节点。利用与双出口贮箱相同的建模方法,可以得到四出口贮箱的动力学方程。
(1)动力学方程
(9)
式中:pf 1,wf 1,pf 2,wf 2,pf 3,wf 3,pf 4和wf 4分别为节点f1,f2,f3和f4的脉动压强和重量位移;Ift,Rft,Hft和rfte为四出口贮箱的惯性、阻尼、水头矢量和位移矢径。
(2)四出口贮箱对结构的作用力
(10)
式中:Af 1,Nf 1,Af 2,Nf 2,Af 3,Nf 3,Af 4和Nf 4分别表示节点f1,f2,f3和f4的截面积和方向向量。
3)三通-可压缩管(双入口单出口)
双入口单出口共有三个节点和一个连接点(见图2(c)),d1,d2,d3和d4,其中d1和d2为推进剂流入节点,d3为流出节点,而d4为组合单元的连接点。
双入口单出口的三通-可压缩管与单入口双出口的三通-可压缩管具有完全相同的结构,仅d2节点的推进剂流动方向发生变化。因此只需令
(11)
单入口双出口的三通-可压缩管动力学方程[15]就可变为双入口单出口的三通-可压缩管动力学方程。
众所周知,经费是开展一切工作的前提和基础,然而经过调查,我国当前基层农机推广中存在严重缺乏经费的现象,从根本上限制基层农机推广服务体系,直接对推广工作的效果产生不良影响。由于经费不足难以对农机技术进行全面演示及推广,导致农民无法认识到其作用,极大地降低农民的购置积极性。除此之外,经费的匮乏还对员工的培训和农机试验等工作产生一定的阻碍,在一定程度上严重制约了基层农机推广服务工作的发展。
(1)动力学方程
(12)
(13)
式中:pd1,wd1,pd2,wd2,pd3,wd3分别为节点d1,d2和d3的脉动压强和重量位移,Itdc,Rtdc,Ktdc和rtde为可压缩管部分的惯性、阻尼、刚度和矢径;Htdc1,Htdc3则表示可压缩管部分入口端到中点处和中点处到出口端的水头矢量。
(2)三通-可压缩管对结构的作用力
KtdcAtdc1(Ntdc1-Ntdc3)(wd1+wd2-wd3)+
(14)

4)弯头-可压缩管
弯头-可压缩管共有两个节点j1和j2与一个连接点j3(见图2(d))。其中j1为推进剂流入节点,j2为流出节点。
弯头的动力学方程可表示为[25]
(15)
式中:pj1,wj1,Aj1,Nj1,pj3,wj3,Aj3,Nj3分别为弯头节点j1和j3的脉动压强、重量位移、截面积和方向向量,rjde表示弯头-可压缩管的矢径。
可压缩管的动力学方程为[8]
(16)
(17)
KjdcAjdc1(Njdc1-Njdc2)wj3+KjdcAjdc1(Njdc2-
(18)
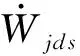
将式(15)~(18)联立可得,弯头-可压缩管的动力学方程。
(1)动力学方程
(19)
Kjdcρg(Aj3Njdc1-Aj1Nj1)·rjde
(20)
(2)弯头-可压缩管对结构的作用力
考虑到弯头对结构的作用力很小,建模过程中仅考虑可压缩管部分对结构的影响,所以弯头-可压缩管对结构的作用力形式上与式(18)完全相同。
单元划分后,对单元和节点进行编号,并以相同节点处脉动压强相等作为连接条件,联立相邻单元的动力学方程。将联立后的方程按照节点编号的顺序对变量进行排序,并将其表示为矩阵形式,便得到不同工作模式下推进系统的动力学方程组[15]
(21)
(22)
(23)
式中:Mp,Cp和Kp分别为推进系统的质量矩阵、阻尼矩阵和刚度矩阵;S表示推力室脉动压强对推进剂脉动重量位移的影响;w是节点脉动重量位移组成的状态矩阵,维数等于节点个数;ptc是推力室脉动压强组成的状态矩阵,包含两部分:氧化剂产生的脉动压强ptco和燃料产生的脉动压强ptcf,其维数等于两倍的推力室个数;fps表示结构系统对推进系统作用的力矩阵;L为燃烧迟滞所产生的系数矩阵,而E表示脉动重量位移对脉动推力的影响;Xps表示结构系统单元与推进系统节点的映射关系,V0,V1和V2是组装过程中形成的系数矩阵,Ф表示为火箭结构系统振型矩阵;q是结构广义坐标组成的状态矩阵,维数等于选取模态的个数。
1.2 结构系统动力学模型
结构的动力学方程为[15]
(24)
式中:Ms,Cs和Ks分别为火箭结构系统的模态质量矩阵、模态阻尼矩阵和模态刚度矩阵;fsp表示推进系统对结构系统作用的力矩阵
(25)
式中:Xf表示推进系统节点与结构系统单元的映射关系;Q0,Q1,Q2,Qp和U为推进系统作用力组装后形成的系数矩阵;rp是推进系统单元的位移矢径组成的矩阵。
1.3 POGO稳定性分析模型
联立式(21)~(25),可以得到动力冗余液体捆绑火箭POGO振动的状态方程[15],即

(26)
式中:
式中:Ew,Eq和Epc表示维数等于节点个数、选取模态数和两倍推力室个数的单位矩阵。
2 算例分析
为研究蓄压器能量值、泵增益和泵柔度对POGO稳定性的影响,定义如下特征阻尼比
ζc=min(ζi(t))
(27)
其中,ζi(t)表示POGO振动系统在t时刻的第i阶阻尼比。当ζc>0,意味着POGO振动系统在任意时刻的各阶阻尼比均大于零,不会发生POGO振动。但当ζc<0时,表明POGO振动系统在某时刻的某阶阻尼比小于零,此时系统会发生POGO振动。ζc越大,最小阻尼比越大,POGO振动系统越不容易发生POGO振动。
2.1 蓄压器能量值对POGO稳定性的影响
蓄压器刚度为[8]
(28)
式中:P0V0为蓄压器能量值,其余变量的定义与文献[8]相同,这里不再累述。
通过增大P0V0可降低蓄压器刚度,减小推进系统频率。当推进系统频率远离结构系统频率时,POGO振动不易发生。图3给出芯级和助推蓄压器P0V0的放大倍数βca和βba在设计值的0.2~5倍时,ζc的变化规律。

图3 蓄压器能量值对三种工作模式下液体捆绑火箭POGO稳定性的影响Fig.3 The effect of accumulator energy on POGO stability of liquid strap-on launch vehicle for three different working modes
图3(a)显示在Mode 1下,增大βca和βba可提高ζc,但当βca>0.8,βba>1.4时,ζc将稳定在2.5×10-5附近。这表明当推进系统和结构系统频率相差较大时,P0V0的变化对POGO稳定性影响较小。此外,芯级蓄压器P0V0对POGO稳定性的影响要弱于助推蓄压器。这是因为助推贮箱和发动机的低阶模态增益系数大于芯级贮箱和发动机的增益系数[26],使得助推管路系统的流量脉动更容易造成POGO振动。Mode 2下ζc随βca和βba的变化规律与Mode 1的结果基本相同(见图3(b)),但最小的ζc为-2.1×10-4,大于Mode 1的-1.3×10-3,这得益于一台助推发动机的故障。由图3(c)可知,Mode 3模式下增大βba或降低βca可提高ζc,但当βca>1.2,βba>1.4时,ζc将稳定在3.4×10-5附近。此外,Mode 3下POGO稳定性对助推蓄压器P0V0的敏感程度强过芯级蓄压器。通过对比图3(a)~图3(c)发现,Mode 3下ζc随βca和βba的最大变化量为2.2×10-4和6.0×10-4,大于Mode 2的1.5×10-4和1.7×10-4,小于Mode 1的3.2×10-4和1.4×10-3。因此,蓄压器P0V0对Mode 1下的POGO稳定性的影响最大,Mode 2下的影响最小。这主要是由于交叉输送管路联通使Mode 2和Mode 3下推进系统频率分布更为分散,变化更为复杂。
2.2 泵增益对POGO系统稳定性的影响
泵增益m+1的提高会增强推进系统和结构系统的耦合强度,对POGO稳定性造成不利影响[9]。图4分析泵增益放大倍数βpg在设计值的1~3倍时,ζc的变化规律。

图4 泵增益对三种工作模式下液体捆绑火箭POGO系统稳定性的影响Fig.4 The effect of pump gain on POGO stability of liquid strap-on launch vehicle for three different working modes
由图4(a)可知,Mode 1下芯级氧化剂泵、芯级燃料泵、助推氧化剂泵和助推燃料泵的βpg的增大均会降低ζc,这与文献[10]中的结论是一致的。此外,助推氧化剂泵的βpg由1增加至3,ζc减少2.0×10-4,大于助推燃料泵的3.3×10-5,芯级氧化剂泵的1.1×10-5,芯级燃料泵的8.0×10-15,这表明氧化剂泵的m+1对POGO稳定性的影响强于燃料泵,助推泵强于芯级泵,这种现象在Mode 2和Mode 3下也存在。燃路系统的阻尼和频率一般高于氧路系统,而且氧路系统的频率更接近结构低阶频率,这会造成氧泵的变化对POGO稳定性的影响更明显。文献[10]指出耦合强度与m+1和模态增益系数的乘积呈正相关,因此具有较大模态增益系数的助推泵的影响强过芯级泵。通过对比图4(a)~图4(c)发现Mode 1下助推氧化剂泵的βpg由1变化至3,ζc减少2.0×10-4,大于Mode 2的4.9×10-5,略小于Mode 3的2.4×10-4。这表明Mode 1和Mode 3下助推氧化剂泵的m+1对POGO稳定性的影响比Mode 2更加灵敏,这是由于Mode 2下一台助推发动机的停机会减弱耦合强度,使得助推氧泵的m+1的影响变小。
2.3 泵柔度对POGO系统稳定性的影响
泵柔度Cpu的增大会降低推进系统频率,进而影响POGO稳定性。图5分析泵柔度放大倍数βpc在设计值的0.5~1.5倍时,ζc的变化规律。

图5 泵柔度对三种工作模式下液体捆绑火箭POGO系统稳定性的影响Fig.5 The effect of pump flexibility on POGO stability of liquid strap-on launch vehicle for three different working modes
图5显示三种工作模式下芯级氧化剂泵的βpc由0.5增加至1.5,ζc几乎不改变,这意味着芯级氧化剂泵Cpu对POGO稳定性的影响较小,这是由于较小的芯级模态增益系数减弱了芯级氧化剂泵对POGO稳定性的敏感程度。助推氧化剂泵的βpc由0.5变化至1.5,Mode 1和Mode 3下ζc增加2.1×10-5和1.9×10-5,Mode 2减少5.1×10-6,这表明Mode 1和Mode 3下助推氧化剂泵Cpu的影响大于Mode 2。氧化剂泵Cpu和蓄压器P0V0都是通过改变氧路系统频率,影响POGO稳定性,因此ζc随氧化剂泵Cpu的变化规律与蓄压器P0V0的影响是基本一致的。助推燃料泵的βpc的增大会降低ζc,其中Mode 2下降低3.3×10-5,大于Mode 1和Mode 3的2.7×10-6和8.0×10-7,也就是说助推燃料泵Cpu的影响在Mode 2下最大,这是因为燃路系统的频率较高,通常比结构的低阶频率高,当燃路系统频率下降时可能会接近结构频率,诱发POGO振动。同时不同工作模式下推进系统频率分布规律相差较大,这影响特征阻尼比对助推燃料泵Cpu的灵敏度。
3 结 论
本文利用改进的Rubin建模方法,建立了独立工作、一台助推发动机故障助推贮箱向芯级发动机供给推进剂和两助推器同时向芯级发动机供给推进剂三种工作模式下,液体捆绑火箭POGO稳定性分析模型。利用QR分解法求解该分析模型,研究POGO稳定性,得到如下结论:
1) Mode 1和Mode 3下,POGO稳定性对助推蓄压器能量值的敏感程度强过芯级蓄压器。Mode 1下蓄压器能量值对POGO稳定性的影响最强,而Mode 2下蓄压器能量值的影响最弱。
2) 三种工作模式下,泵增益的提高均会减弱POGO稳定性,其中氧化剂泵的影响强于燃料泵,助推泵的影响强于芯级泵。Mode 1和Mode 3下泵增益对POGO稳定性的影响比Mode 2更加灵敏。
3) 三种工作模式下,芯级氧化剂泵柔度对POGO稳定性的影响较小。Mode 1和Mode 3下助推氧化剂泵柔度的影响大于Mode 2。助推燃料泵柔度的增大会降低燃路系统频率,可能诱发POGO振动,其中Mode 2下的影响最大。

