充液航天器变质量液体大幅晃动的SPH分析方法

于 强，王天舒

(清华大学航天航空学院，北京 100084)

0 引 言

一直以来，充液航天器贮箱内液体燃料及氧化剂的晃动作用对于航天器的姿轨控制都有着不可忽视的影响，甚至可能导致任务失败，对液体晃动问题进行准确分析具有重要的意义。许多学者都对该问题进行了研究。

等效力学模型方法是目前广泛应用于航天领域液体小幅晃动分析的研究方法[1-3]，目前也拓展到了液面非线性不太强的大幅晃动问题中[4-5]。然而，当航天器在进行变轨或软着陆等较大幅度机动的时候，可能会激发贮箱内液体的强非线性晃动，甚至产生液面翻卷破碎的现象。此时等效力学模型不再适用，合理快速的数值仿真方法研究有其必要性。此外，航天器在进行大幅度机动的时候往往伴随着燃料的消耗，贮箱内的液体质量在不断减少，所以对液体晃动的数值仿真方法还要考虑变质量的因素。

基于网格的计算流体动力学方法(CFD)是处理液体晃动问题的一类常用方法，如任意拉格朗日-欧拉(ALE)方法[6]。但网格类方法处理自由液面非线性很强的情况，需要很精细的网格划分才能比较好地刻画自由液面，会降低计算效率，在实际工程应用时有一定的局限性。光滑粒子流体动力学(SPH)方法是一种基于拉格朗日描述的无网格粒子类方法，适合自由表面流动问题的仿真[7]。其特点是将流体离散成一系列任意分布的粒子，并利用空间核函数近似以及粒子求和近似估算场函数及其空间导数。粒子之间不存在物理上的连接，在计算大变形自由液面问题时存在优势。

变质量晃动问题反映在SPH方法中是流出流量可控的开口边界问题。边界条件处理一直都是SPH方法的重要研究方向，大致可分为固壁和开口两类。目前为止，SPH处理固壁边界的方法主要可以分为两大类，第一类是设置虚粒子的方法，主要有三种实现方式：一是边界虚粒子对流体粒子直接建立斥力模型[8]，阻止粒子穿透边界；二是认为相对静止的边界虚粒子具有流体粒子的性质[9-10]，通过计算合理的边界虚粒子压力阻止流体粒子流出；三是通过设置与流体粒子相对于边界对称的镜像虚粒子，使得流体粒子在固壁边界处形成近似反弹的效果以达到固壁边界条件的实现[11]。第二类方法是一致化半解析边界条件(Unified semi-analytical wall boundary conditions, USAW)处理方法[12]。在该方法中，边界是按照网格进行划分，核函数近似解在边界被截断的部分离散到边界网格节点上，进而推导出边界上的控制方程。相比于虚粒子设置方法，USAW方法具备一定的数学理论基础，可以比较准确地反映固壁边界附近的流动，并描述任意纽曼(Neumann)或狄利克雷(Dirichlet)边界条件，但该方法在计算效率方面相对于虚粒子方法有明显不足。Mayrhofer等[13]将USAW方法应用到了三维情况，拓展了其应用范围。骆钊等[14]在USAW方法基础上提出了无质量边界粒子概念，避免了边界零粒子层现象。

对应固壁边界条件，SPH方法对于开口边界条件的处理方法也主要分为虚粒子类方法和半解析类方法两类。前者主要采用设置缓冲层并填满虚粒子的处理方式[15]，借鉴网格类处理开口边界的思想，为缓冲层虚粒子设置满足边界物理条件的物理量，缓冲区粒子参与SPH计算。该方法实现简单，但由于粒子的离散特性，难以准确描述边界处的流量。后者则利用USAW方法的处理思想控制开口边界处的流量以实现开口边界条件。Leroy等[16]结合ISPH方法和USAW条件，实现了二维及三维情况下定流速开口边界工况的计算，并得到了很好的效果。但是，半解析的开口边界处理方法在实际应用时，尤其对于三维情况，庞大的计算量限制了其在实际工程领域上的应用。

针对充液航天器燃料消耗过程中大机动可能引起的液体晃动问题，本文出于对计算效率以及与航天器动力学程序联合仿真的需求，在非惯性系下SPH(Non-inertial SPH, NI-SPH)方法[17]的基础上，对虚粒子类开口边界处理方法进行了改进，使其能够准确控制出口边界处的流量，从而实现变质量液体晃动的SPH仿真。此外，本文还利用变质量质点系的动量和动量矩定理计算了液体晃动的作用力及作用力矩，与航天器系统动力学仿真程序形成了闭环。最后，通过将仿真结果与CFD商业软件Flow-3d结果进行对比，验证了算法的有效性。

1 控制方程

1.1 SPH方法基本理论

标准SPH方法是将液体部分离散成一系列具有质量的拉格朗日粒子，不存在碰撞体积，然后利用核函数近似和粒子求和近似的方法用粒子所携带的物理量对宏观物理量f(xi)(如密度、压强等)及其空间导数进行近似，形式如下：

(1)

(2)

其中，下标代表粒子编号，Wij=W(xi-xj,h)为核函数；x，ρ，m分别表示相应粒子的位置向量、密度和质量；h表示核函数的光滑长度，根据核函数的不同，其作用范围，即支持域的半径为κh(κ取2或3)，h一般可以取粒子初始间距r0的倍数，即h=kr0；N为粒子i支持域内的粒子数目；此外，有

(3)

本文的核函数采用的是目前最为广泛的B-样条函数(取κ=2,k=1.3)，如下所示：

(4)

其中,R=r/h，r为粒子间距；对于一维、二维和三维问题分别有

(5)

1.2 N-S方程的SPH离散形式

利用SPH近似方法对拉格朗日描述下Navier-Stokes方程进行离散，可以得到N-S方程的SPH离散形式[18]：

(6)

Γi+fout,i

(7)

其中,v和fout分别代表速度矢量和重力产生的加速度，物理量的下标ij代表粒子i和j的相应物理量之差。Γi为简化的物理黏性耗散项，采用由Lo和Shao[19]提出的公式：

(8)

式中：ν是液体的运动黏性系数。

1.3 压力计算方法

SPH方法在计算不可压缩流体问题时，通过引进人工压缩率将不可压缩流近似看作弱可压流体。对于一般液体的晃动问题，本文采用下面的状态方程由密度变化显式计算压力[20]：

(9)

式中:ρ0是液体初始密度；γ为常数，一般γ=7；pb为背景压力，一般可置为0，式(9)计算的便是流体的相对压力场；cs为人工声速，本文取cs=15。γ和cs的选取决定了液体的刚性，限制液体粒子的密度变化率在1%之内，能够保证流体的弱可压性质。

2 边界处理方法

由于SPH离散粒子的拉格朗日性质，SPH方法在表面张力作用不明显的情况下可以自然满足自由边界条件，而对于固壁边界条件和流量可控的出口边界条件，本文均基于虚粒子类方法进行了实现。

2.1 固壁边界条件

基于边界虚粒子的设置，本文采用的固壁边界处理方法详见文献[10]。考虑无滑移边界条件，给边界虚粒子设置了与镜像虚粒子边界处理方法意义类似的镜像速度：

(10)

其中，w代表边界虚粒子。该速度用于方程(6)和(8)的计算，但不用于虚粒子相对位置更新，边界虚粒子在非惯性系下的位置始终保持不变。

边界虚粒子的压力则需要较好地描述固壁边界附近的液体压力梯度，综合考虑非惯性系下的惯性力和重力，边界虚粒子的压力由SPH方法离散得到：

(11)

边界虚粒子的密度根据式(11)求出的压力，利用式(9)的反函数计算得到。边界虚粒子参与流体域实粒子的SPH计算，可以在没有强冲击的情况下有效防止流体实粒子的非物理穿透，这种处理方法对于充液航天器贮箱内液体晃动仿真非常适用。

2.2 流量可控的出口边界条件

由于SPH粒子的离散性质，SPH方法中的物理量分布是离散的，不是连续变化的，难以准确刻画一个截面上物理量的变化率，因此基于虚粒子设置的缓冲层开口边界处理方法在处理控制边界流量的开口边界问题有着天然的劣势，无法像网格类方法简单地在边界结点处设置固定速度。

针对这一问题，本文将贮箱及缓冲层区域(可认为是贮箱出口管)统一用固壁边界虚粒子封闭，正常情况下均按照SPH控制方程进行计算。在每一个航天器动力学时间步Δtd(远大于SPH仿真时间步)中，根据所给的当前时刻充液比σ，计算得到该动力学时间步要流出流体区域的粒子数目：

(12)

其中，N和N0分别是上一时刻剩余的流体粒子数和初始流体粒子数；σ0是初始的充液比；方括号代表高斯取整函数。根据需要流出粒子的数目ΔN，在缓冲层流出边界的邻近网格(链表搜索法搜索邻近粒子对设置的网格)中搜索最接近边界的ΔN个粒子设置为边缘流出粒子，如图1所示，记录此时这些粒子与边界的垂直距离分别为si0,i=1,2,…,ΔN。这些粒子具有如下性质：

图1 流出边界附近的粒子分布示意图Fig.1 Particles distribution near the outlet boundary

1)解除边界虚粒子对边缘流出粒子的影响，该类粒子具备垂直于流出边界向外的速度，其大小为

vi=si0/Δtd

(13)

2)边缘流出粒子的压力和密度分别按照固壁边界条件的方法进行计算。

3)边缘流出粒子对于其他流体粒子的作用均乘以一个衰减系数ξi，该系数由粒子与流出边界的实时距离si计算得到，其表达式为：

ξi=(esi/si0-1)/(e-1)

(14)

第一条性质使得边缘流出粒子能够在该动力学时间步的计算后运动到边界处，进而被设置成场外粒子，不再参与计算。而后两条性质则是在保持边缘流出粒子对于缓冲层粒子作用的同时，保证边界虚粒子对缓冲层其他流体实粒子的阻挡作用依然合理。该方法可以有效控制流出边界的流量，并让出口边界附近的流场比较合理，减少数值震荡。这种离散的边界处理方法是基于SPH粒子进行人工操作的，数学上不能严格对应流体在边界处要满足的方程，但由于缓冲层的存在，这种人工处理方法对于贮箱内流体实粒子的扰动很小，可以适用于充液航天器内的变质量液体晃动问题。此外，方法中衰减系数的表达式也可以采用其他类型函数，满足初始为1，粒子到达边界时为0即可。

3 变质量液体晃动作用力及力矩的求解方法

在实际的应用当中，航天器的姿态信息变化是比较复杂的，动力学闭环仿真中的晃动仿真模块需要通过航天器的姿态信息和充液比，反馈该时刻液体晃动对航天器产生的作用力和作用力矩。本文采用非惯性系下的SPH方法[16]，根据航天器姿态信息对每一个流体实粒子施加惯性力Finertial,i：

Finertial,i=-mi·

(15)

式中:V0是航天器质心的平动速度，dV0/dt为航天器质心的绝对加速度，ω和β分别为航天器质心本体坐标系的角速度和角加速度的矢量形式，ri为流体实粒子在航天器质心本体坐标系下的位置矢量，vi为流体实粒子相对于航天器质心本体坐标系的相对速度矢量。

至于液体晃动作用力及作用力矩的求解，本文采用了变质量质点系的动量定理及动量矩定理进行计算，不计算缓冲层流体实粒子的动量和动量矩，在每一个航天器动力学时间步Δtd中对累积流出贮箱进入缓冲层的粒子动量和角动量求和，分别得到ΔPout和ΔLout，则该时间步内液体晃动对于航天器产生的作用力Fslosh及作用力矩Mslosh分别为：

(16)

(17)

式中：N为该动力学时间步计算之后的贮箱内流体实粒子数目，Δ后加括号表示括号内物理量在该时间步的变化量，finertial,i和fout,i分别为第i个流体实粒子所受惯性力和重力导致的加速度。

SPH仿真液体晃动的计算模块可以作为一个反馈模块反映液体晃动产生的影响，与航天器系统动力学仿真形成一个闭环，从而实现两者的联合仿真。

4 算例分析和讨论

本文所有算例测试均在一台配置4核8线程4.20 GHz主频的Intel i7处理器和16 GB内存的个人电脑上完成。根据文献[21]中的验证，非惯性系下SPH方法可以在粒子初始间距较大，即粒子数较少的情况下得到合理的结果。为了体现算法的效率，本文算例采取了粒子初始间距较大的情况(将粒子初始间距选为贮箱半径的1/10左右)。此外，算例以CFD商业软件Flow-3d的计算结果作为参照，该软件采用了VOF方法计算自由表面流，在仿真贮箱内液体晃动问题上有稳定良好的表现。

4.1 常重环境球形贮箱短时间仿真

球形贮箱的半径为0.62 m，贮箱中心位置为(0.62，0.62，0.62)m，液体为水，其密度为1000 kg/m3，动力黏性系数为9.29×10-4kg/(m·s)。粒子初始间距为0.05 m，初始充液比为15%，设置了1322个实粒子(包括缓冲区)和2284个边界虚粒子。初始状态下的液体分布及相应SPH粒子离散如图2所示。

图2 球形贮箱初始液体及SPH粒子分布图Fig.2 Initial liquid and SPH particles distribution in the sphere tank

仿真时间为10 s，充液比从15%匀速减少到5%。考虑环境为常重环境，重力加速度g=9.8 m/s2，垂直初始水平液面向下(设为z轴负方向)，然后在水平x和y方向(与z方向构成了贮箱的随体坐标系)分别施加强制的简谐振动，振动位移形式分别如下所示：

x=0.15sinπt

(18)

y=0.1sin0.25πt

(19)

预平衡仿真时间2 s(实际仿真前仅施加重力进行的初始状态计算)，动力学时间步长为0.01 s，SPH仿真时间步长Δt由CFL(Courant-Friedrichs-Lewy)稳定性条件[22]决定：

(20)

式中:h为光滑长度，cs为人工声速,vi为粒子i的速度大小。

仿真实际用时52 s，效率上能够达到嵌入航天器动力学仿真的要求。表1展示了部分时间点， SPH计算得到的液体粒子分布与Flow-3d计算结果的对比图吻合程度较好，SPH方法可以比较好地刻画自由液面的非线性现象。晃动作用力及力矩在贮箱随体坐标系下投影的对比曲线如图3和图4所示。

表1 常重情况下球形贮箱内变质量液体晃动：SPH方法与Flow-3d液面对比Table 1 Variable-mass liquid sloshing in the sphere tank under normal gravity: SPH results of flow patterns in comparison with those from Flow-3d

由图3～图4可知，此时SPH方法求解得到的晃动作用力及力矩曲线与Flow-3d仿真结果吻合良好，计算精度可以得到保证。相比于Flow-3d的计算结果，SPH求解得到的三轴晃动作用力峰值的相对偏差分别为0.94%，15.74%，9.72%；三轴晃动作用力矩峰值的相对偏差分别为8.64%，9.05%，2.12%。其中相对偏差最大的是水平y方向上的作用力，这主要是由于y方向上的激励加速度峰值是事实上，包括SPH方法在内的粒子类方法会有比网格类方法更强的数值振荡，即便采用数值耗散的方法，也会使计算得到的晃动作用力及力矩存在小幅高频的非物理振荡。但是，该振荡没有改变作用力变化趋势，且不会累积冲量，在晃动幅度较大方向上衰减明显，对整体计算结果不会产生显著影响。总体而言，对于常重环境下的变质量液体晃动问题，本文提出的方法能够得到合理的计算结果。

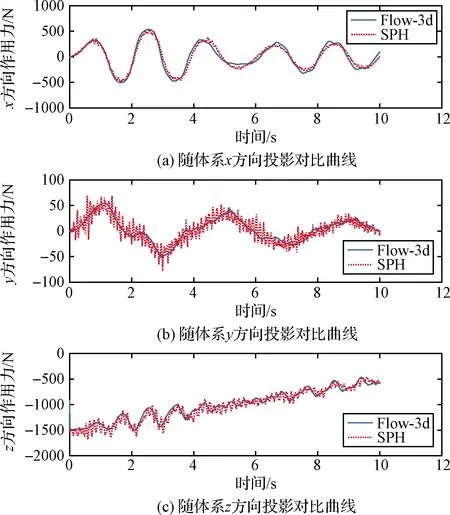
图3 常重环境SPH方法与Flow-3d仿真球形贮箱内变质量液体晃动的作用力对比曲线Fig.3 Comparison of variable-mass liquid sloshing force histories predicted by the SPH and those simulated by Flow-3d in the sphere tank under normal gravity

图4 常重环境SPH方法与Flow-3d仿真球形贮箱内变质量液体晃动的作用力矩对比曲线Fig.4 Comparison of variable-mass liquid sloshing moment histories predicted by the SPH and those simulated by Flow-3d in the sphere tank under normal gravity

x方向上的1/24，主要的晃动现象会呈现在x这一个方向上(见表1)。从曲线可以看出实际计算的y方向上晃动作用力量级大约是x方向上的1/10，其大小受离散粒子产生的数值振荡影响相对较大。

4.2 低重环境卡西尼贮箱长时间仿真

卡西尼(Cassini)贮箱的中间段为圆柱，两端为半球，在航天器中有广泛的应用。本节针对卡西尼贮箱在低重环境下的复杂激励情况，进行了长时间的变质量液体晃动仿真。

设置卡西尼贮箱的半球及圆柱段半径为0.492 m，圆柱段的高度为0.1 m，贮箱几何中心在航天器质心本体坐标系中的位置坐标为(0.0，-0.875，-0.681)m。液体为航天器中常用的燃烧剂甲基肼(MMH)，密度为874.4 kg/m3，动力黏性系数为8.50×10-4kg/(m·s)。初始充液比为60%，仿真时间为300 s，匀速减少到35%。粒子初始间距为0.045 m，初始共设置了3324个流体实粒子(含缓冲层)和1982个虚粒子，初始状态下的液体分布及相应SPH粒子离散如图5所示。

图5 卡西尼贮箱初始液体及粒子分布图Fig.5 Initial liquid and particles distribution in the Cassini tank

实际航天器在进行变轨或软着陆时除了用推进的方式，还会使用动量轮调整姿态。算例采用了复杂的运动形式作为激励输入，航天器的质心平动加速度以及姿态变化规律在贮箱随体坐标系下的投影如图6和图7所示(垂直于初始液面向上为z轴正方向)。

图6 航天器质心的平动加速度Fig.6 Translational acceleration of the spacecraft mass center

图7 航天器角速度Fig.7 Angular velocity of the spacecraft

SPH仿真实际用时2795 s，约为仿真时间的9倍，效率能够满足闭环仿真。计算得到的晃动作用力及力矩在贮箱随体坐标系下的投影与Flow-3d计算结果对比曲线如图8和图9所示。

图8 低重环境SPH方法与Flow-3d仿真卡西尼贮箱内变质量液体晃动的作用力对比曲线Fig.8 Comparison of variable-mass liquid sloshing force histories predicted by the SPH and those simulated by Flow-3d in the Cassini tank under low gravity

图9 低重环境SPH方法与Flow-3d仿真卡西尼贮箱内变质量液体晃动的作用力矩的对比曲线Fig.9 Comparison of variable-mass liquid sloshing moment histories predicted by the SPH and those simulated by Flow-3d in the Cassini tank under low gravity

从图8～9可以看出，整体上SPH计算得到的结果与Flow-3d计算结果吻合较好；相比于Flow-3d计算结果，SPH方法求解得到的三轴晃动作用力峰值相对偏差分别为1.64%，10.50%，5.80%；三轴晃动作用力矩峰值的相对偏差分别为6.93%，2.12%，1.35%。

为了更清晰地区分两种仿真结果，对图8进行了局部放大，选取100～150 s区间内的结果如图10所示。

图10 低重环境SPH方法与Flow-3d仿真卡西尼贮箱内变质量液体晃动的作用力局部对比曲线Fig.10 Comparison of variable-mass liquid sloshing local force histories predicted by the SPH and those simulated by Flow-3d in the Cassini tank under low gravity

两种仿真结果变化趋势吻合良好，但通过进一步观察，可以发现随着时间的推移，两种仿真结果差异有明显的增大趋势，尤其是z方向上的晃动作用力，在仿真最后已经可以观察出有明显的偏移。经过检查，发现Flow-3d在计算长时间自由表面流动的时候，由于自由液面处网格之间的流量计算存在误差，会出现比较明显的体积计算误差。针对本算例，Flow-3d中液体体积在300 s的仿真过程中大约增加了7%，后期的实际液体体积大于既定值，最后的晃动作用力及力矩也因此相对偏大。当仿真时间进一步加长时，Flow-3d的体积累积误差会进一步增大。此外，根据实际测试，当自由液面面积更大，变化更加剧烈的时候，液体体积的计算误差累积速度也会变得更快。因此，考虑到SPH粒子系的质量守恒性，SPH方法在长时间仿真时具有更好的稳定性。

综上所述，本文提出的算法能够解决低重环境复杂激励下长时间变质量液体晃动的动力学问题，对充液航天器贮箱内变质量液体晃动的仿真分析十分有效。

5 结 论

本文基于非惯性系下SPH方法的基本理论，针对存在燃料消耗的充液航天器大幅机动情况，提出了一种可以控制流量的虚粒子类出口边界处理方法。该方法能够根据输入的航天器姿态信息和充液比，完成单动力学时间步的SPH更新，并采用变质量质点系动量定理和动量矩定理计算并输出晃动作用力及力矩，与航天器系统动力学仿真形成闭环。

最后通过与商业软件Flow-3d计算结果的对比，该算法对于解决充液航天器贮箱内变质量液体大幅晃动问题的适用性和有效性得到了验证。

SPH方法能够较好地解决常重及低重环境下的液体晃动问题，但对于微重环境表面张力作为主要驱动力的情况还未有简洁有效的处理方法，这也是今后需要研究的重要方向。