双天线GPS/MEMS-INS深组合导航方法研究
龙 腾,穆荣军,苏炳志,崔乃刚
(哈尔滨工业大学航天学院,哈尔滨 150001)
0 引 言
近年来随着卫星导航技术的高速发展和中国自主研发的北斗卫星导航系统全球组网,卫星导航的应用越来越广泛,尤其是在车辆和无人飞行器导航领域。GPS/MEMS-INS(Global Position System, Micro-Electro-Mechanical System, Inertial Navigation System)组合导航作为一种经典的导航系统解决方案,以其低成本、高精度、全维度的特点被广泛研究和应用。其组合方式存在三种:松组合、紧组合和深组合。目前普遍采用的松组合和紧组合方式在实际应用中会面临两个主要问题:一是在这两种组合方式中,卫星接收机都是作为一个独立的设备提供卫星导航测量信息,组合导航的精度主要依赖接收机的性能,当处于信号遮挡、衰减、多径的环境时,接收机极易受到干扰,导致可见卫星数量较少甚至无法定位,从而影响组合导航的输出;二是当组合导航系统的惯性器件为MEMS器件时,由于其精度性能较差,单天线卫星接收机只能提供位置、速度信息,组合导航的航向精度很难提高[1]。针对这两个问题,本文对双天线GPS/MEMS-INS深组合导航方法进行研究,通过深组合技术提升卫星接收机在复杂环境下的信号跟踪性能,利用双天线载波相位差分提高组合导航系统的航向精度。
惯性/卫星深组合技术基于矢量跟踪方法[2],是目前最先进的卫星导航信号处理技术,自1996年被提出以来受到众多学者的关注[3]。矢量跟踪改变传统标量跟踪各卫星通道彼此独立的结构,对所有通道进行联合跟踪[4],通过引入惯导辅助的信号跟踪环路,实现惯性导航和卫星导航之间更深的数据融合,具有弱信号跟踪[5]、高动态跟踪[6]、桥接中断信号[7]等优点。矢量跟踪深组合主要分为两大类:集中式深组合和级联式深组合。集中式深组合以基带I/Q数据作为导航滤波器的量测量,导航滤波器控制所有通道本地码和载波的生成,虽然能在原始数据处实现最深层次的组合,但其滤波器维数大、更新率高、非线性强,难以工程应用[8]。级联式深组合采用联邦滤波思想,先将基带信号预处理,再进行组合导航滤波。根据预处理方法分为基于鉴别器的级联式深组合和基于预滤波器的级联式深组合[9]。由于预滤波器在应用时对滤波参数敏感[10],所以本文采用基于鉴别器的方式设计深组合卫星信号跟踪环路,使其结构简单、具有更强的鲁棒性。根据信号强度设计三种跟踪结构,通过信号强度判别方法在线切换,解决深组合导航滤波器易受失准通道量测影响、抗差性能较差[11]的问题。
双天线或多天线载波相位差分是卫星导航姿态测量的主要手段[12]。如果用双天线载波相位差先计算载体的姿态角,再作为深组合导航滤波器的量测量,在计算姿态角阶段需使用复杂的整周模糊度搜索算法和周跳检测修复算法[13]。这不仅增大了系统复杂度,还带来了不稳定因素。本文将双天线载波相位差直接作为导航滤波器的量测量,避免姿态角的计算,同时可根据惯导预测的姿态检验当前测量的相位差是否存在整周误差,并及时修正。针对实际应用中出现的相位差测量俯仰不准而影响导航滤波器俯仰角估计的问题,构造了视线矢量水平投影矩阵,对相位差量测方程进行线性变换,使得变换后的相位差量测量不再包含俯仰信息,实现在不对俯仰角造成干扰的条件下修正航向角误差。
因为实现深组合导航系统涉及到卫星接收机的改造,使用软件无线电技术具备开发灵活度高的优点[14],所以文章最后基于软件无线电开发了双天线GPS/MEMS-INS深组合导航车载试验系统,通过开展城市中的跑车试验,验证了所设计的深组合导航算法在复杂环境中的信号跟踪和导航能力。
1 双天线GPS/MEMS-INS深组合系统方案设计
图1所示为双天线GPS/MEMS-INS深组合导航系统的总体方案。
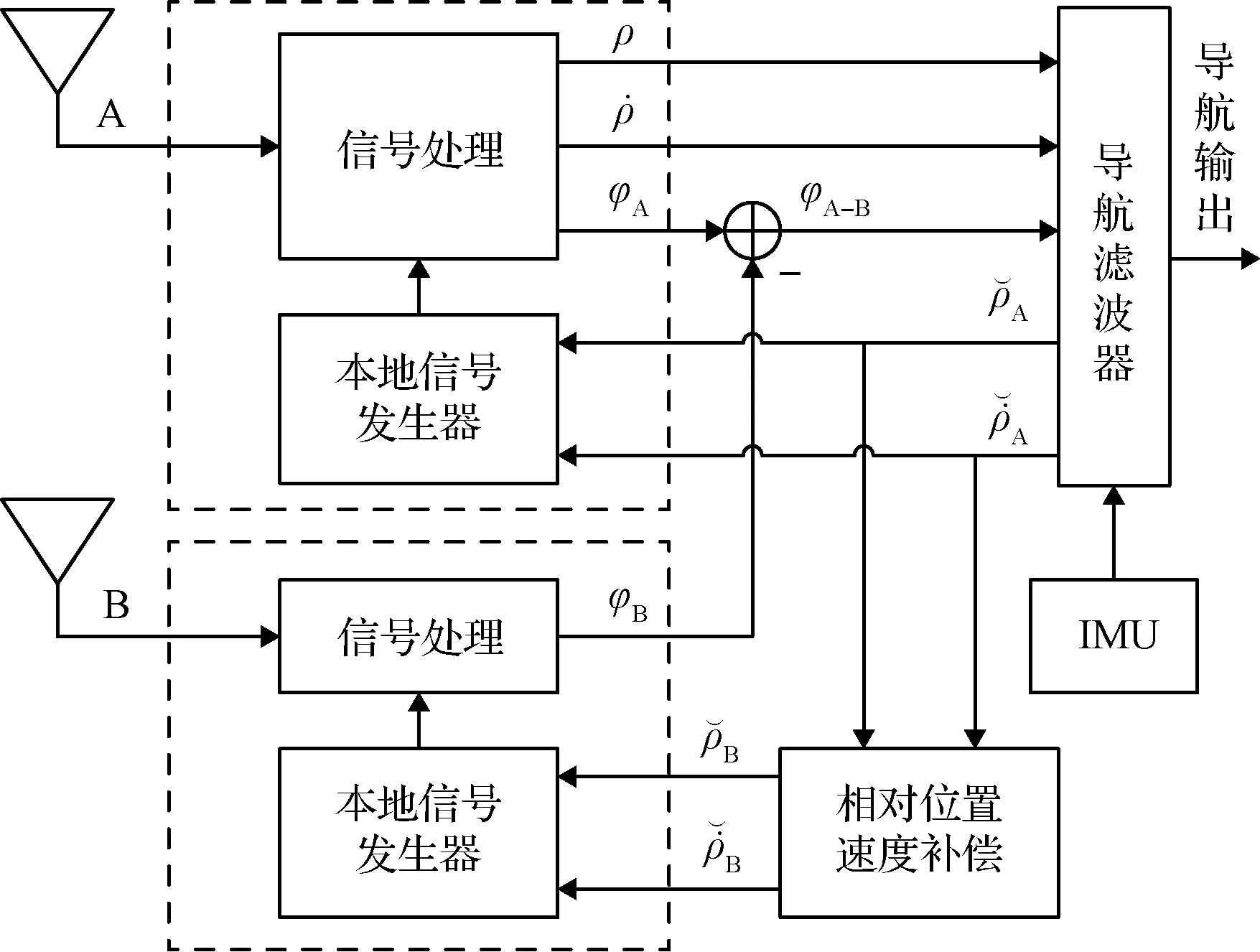
图1 双天线GPS/MEMS-INS深组合导航系统总体方案Fig.1 Dual-antenna GPS/MEMS-INS deeply-coupled navigation system architecture
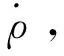
2 矢量跟踪环路设计
2.1 矢量跟踪环路结构
将信号按强度分为三个等级:强信号、弱信号、失锁状态。强信号表现为载噪比较大,使用传统跟踪环路可以稳定跟踪;弱信号表现为载噪比较小或信号存在较大波动,载波跟踪可能不稳定;失锁状态表现为信号很弱导致无法被跟踪。
在基于二阶锁相环的传统跟踪环路(见图2)基础上,针对上述信号特性,设计了三种矢量跟踪结构,如图3~图5所示。
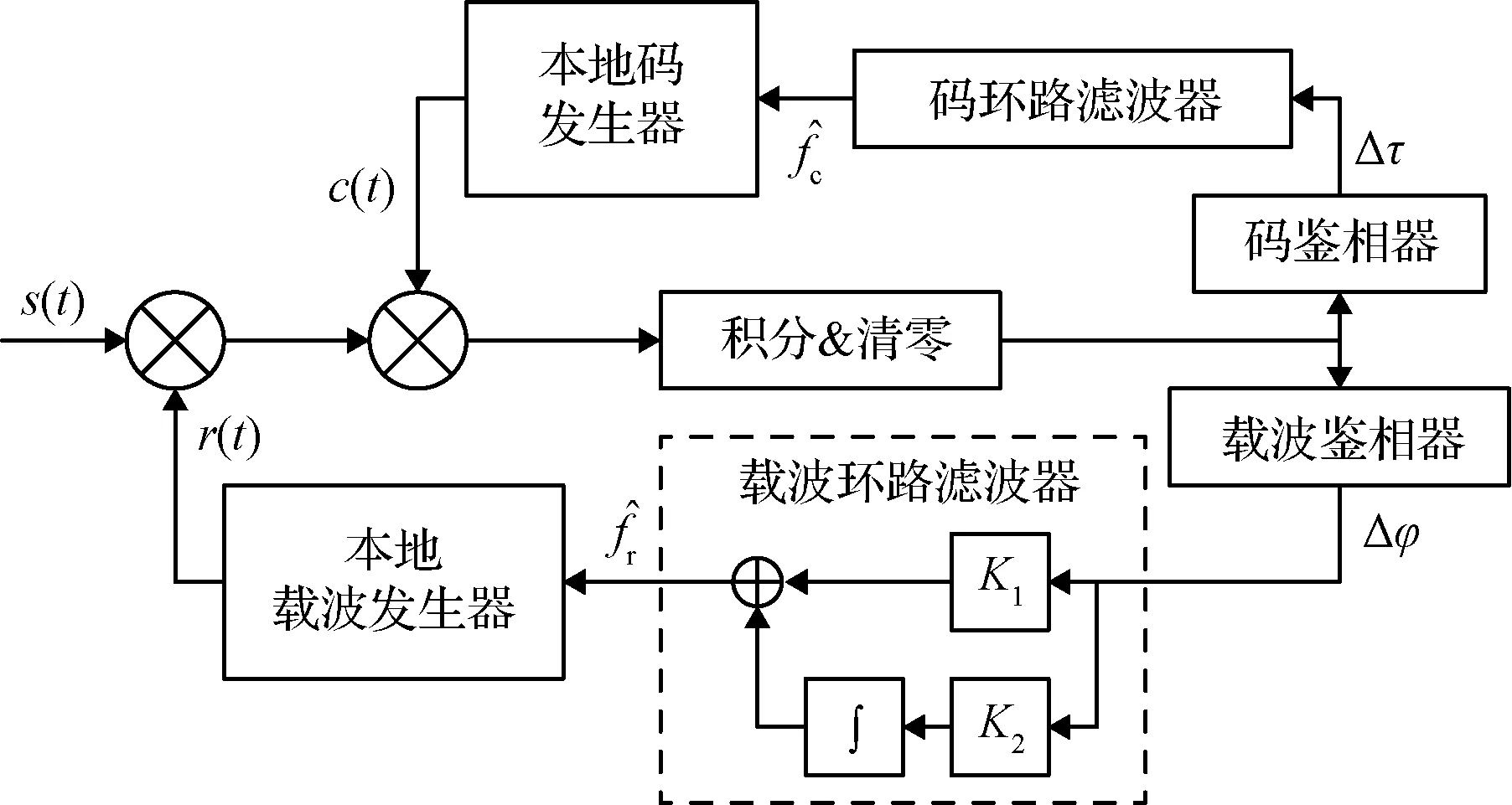
图2 基于二阶锁相环的传统跟踪环路Fig.2 Traditional tracking loop based on second-order PLL
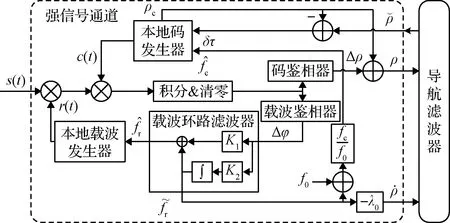
图3 强信号通道矢量跟踪环路Fig.3 Vector tracking loop in strong signal channel
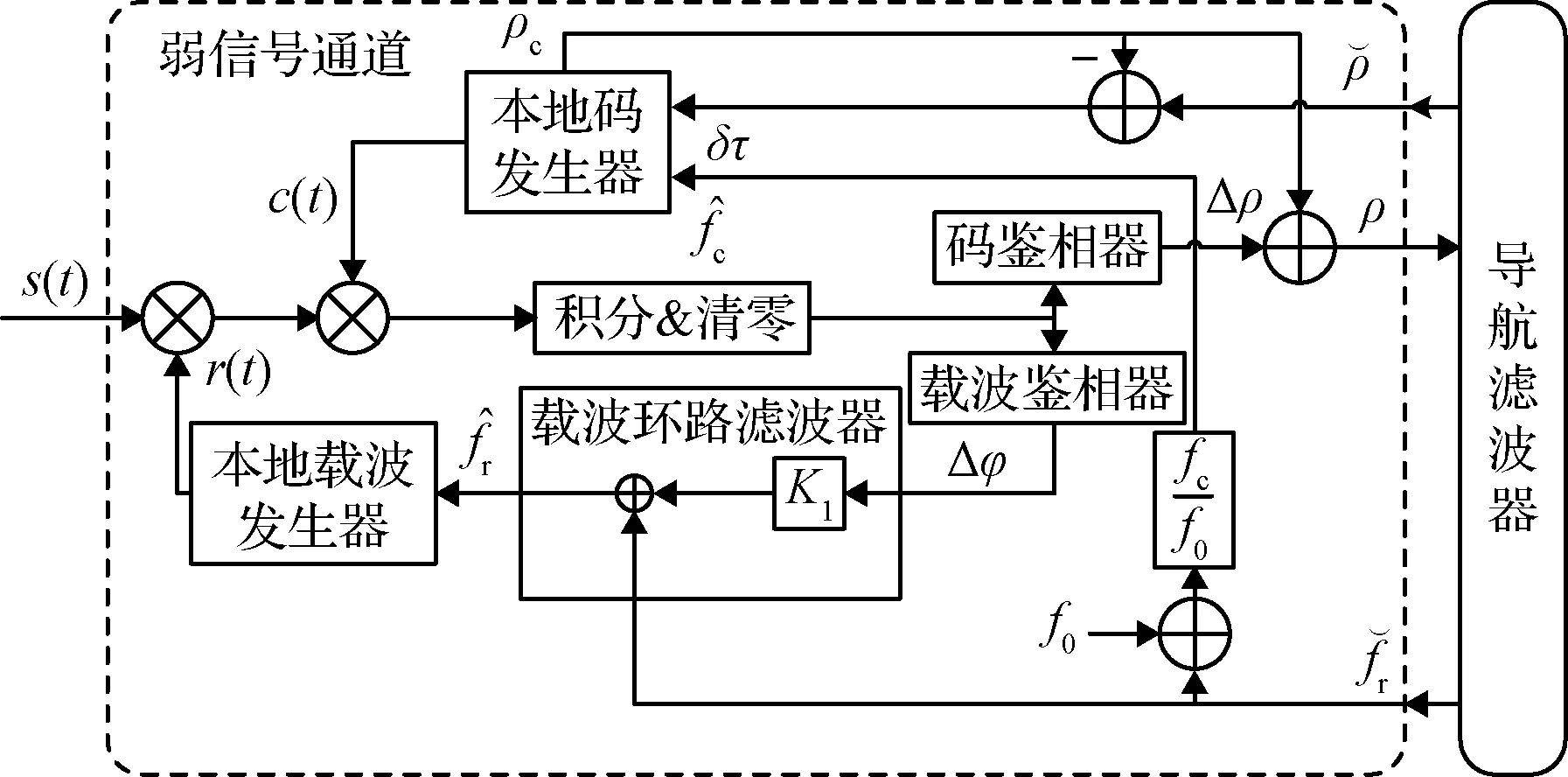
图4 弱信号通道矢量跟踪环路Fig.4 Vector tracking loop in weak signal channel
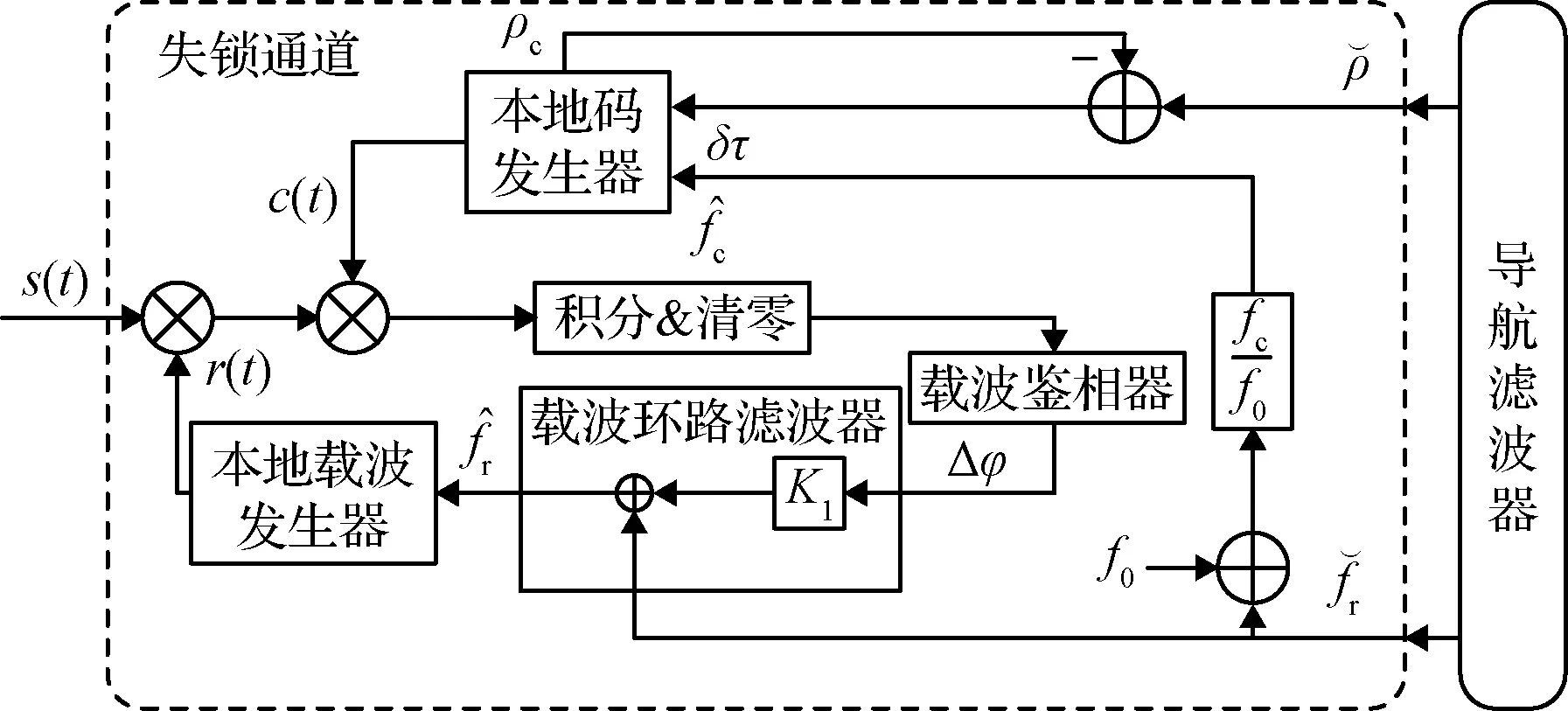
图5 失锁通道矢量跟踪环路Fig.5 Vector tracking loop in loss-of-lock channel
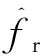
在所有信号强度下,码跟踪统一采用矢量码跟踪环。将传统码跟踪环断开,去掉码环路滤波器,本地码发生器由载波频率计算的码频率直接驱动。取本地码发生器码相位计算的伪距加上码鉴相器输出折算成的伪距误差作为所在通道的伪距测量值,输入导航滤波器。导航滤波器根据当前位置计算所有通道的理论伪距,理论伪距与码相位计算的伪距做差得到码相位误差,用于修正本地码发生器的码相位。由于失锁通道无法测量到真实信号,所以不再向导航滤波器提供伪距输出,只做码相位修正,保证在失锁期间跟踪码相位,等待信号恢复。由于信号跟踪的处理周期要快于导航滤波器的更新周期,通过码鉴相器获得伪距误差可以取滤波更新周期内码鉴相器输出的均值,以降低伪距测量噪声。
对于载波跟踪,为提高导航速度精度,本文并未引入矢量锁频环,而是在强信号时保留传统二阶锁相环独立跟踪。主要基于以下原因:若构造矢量锁频环,需要像码环一样将载波环打开,通过载波鉴相器或鉴频器得到当前载波频率误差,从而得到伪距率测量值。但这样测量的伪距率噪声较大,导致导航滤波器输出的速度噪声也较大。若用二阶锁相环先测出伪距率,再传给导航滤波器处理,相当于对速度进行了两次滤波,可以将最终的速度噪声压制到较低的水平。
虽然锁相环跟踪精度高,但也很脆弱,当信号较弱时,容易出现跟踪不稳定的现象,所以弱信号和失锁通道使用频率辅助载波跟踪环。导航滤波器根据当前速度计算理论伪距率,驱动本地载波发生器,使用载波相位的比例控制实现载波相位跟踪。在数学模型上相当于速度前馈的一阶锁相环,如图6所示(图中vφ为载波相位噪声,vf为载波频率噪声,φi为实际信号的载波相位,φo为本地载波发生器的载波相位)。由于载波环路滤波器中没有积分器,不会出现因为一段时间的弱信号导致积分器积分值误差过大的情况。这种跟踪环路无论信号多么弱,甚至失锁均可保持运行,一旦信号恢复,一阶环路会迅速完成相位锁定。
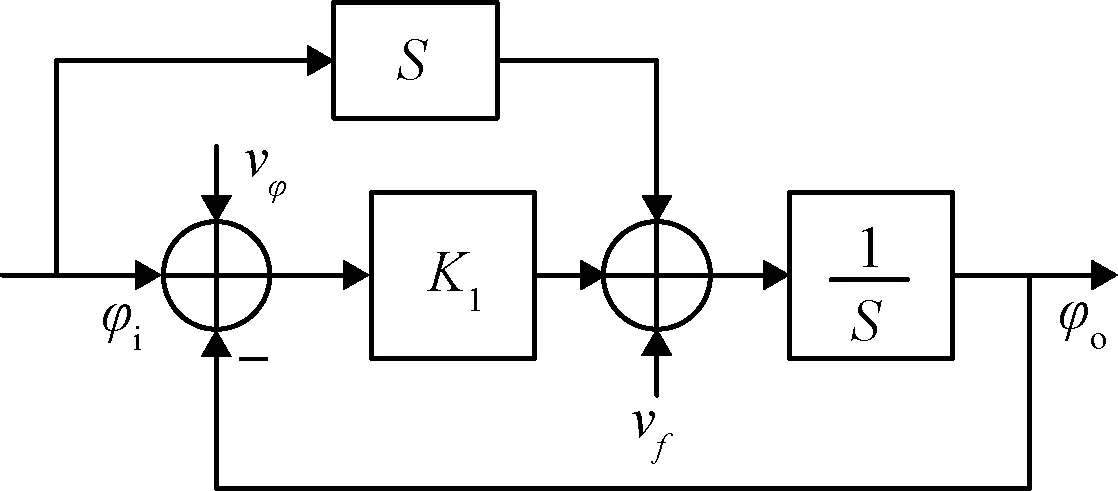
图6 速度前馈一阶锁相环系统模型Fig.6 Velocity feedforward first-order PLL model
本文所提出的矢量跟踪环路具有下述优势:
1) 矢量码跟踪环利用接收机位置将所有通道的码跟踪耦合在一起,使码跟踪精度不再依赖信号强度,即使弱信号和失锁通道均能保持良好的码相位跟踪,信号恢复时不必重新进行码相位搜索。
2) 载波跟踪采用传统二阶锁相环和频率辅助载波跟踪环两种策略,不仅提高了导航速度精度,还能在弱信号和失锁时维持载波跟踪,信号恢复时也能迅速重新锁定载波相位。
3) 将信号强度分级,只容许误差小的测量值进入导航滤波器参与导航修正,解决不良信号污染滤波器的问题,保证滤波器的稳定性和导航精度。
4) 避免复杂的预滤波器设计,在保证跟踪性能的基础上简化矢量跟踪结构,降低系统复杂度,使其更容易工程实现。
2.2 信号强度判别
为在线判别信号强度,本节提出利用瞬时载噪比、平均载噪比、一个比特内I路数据的符号变化进行综合判别的策略,如图7所示。
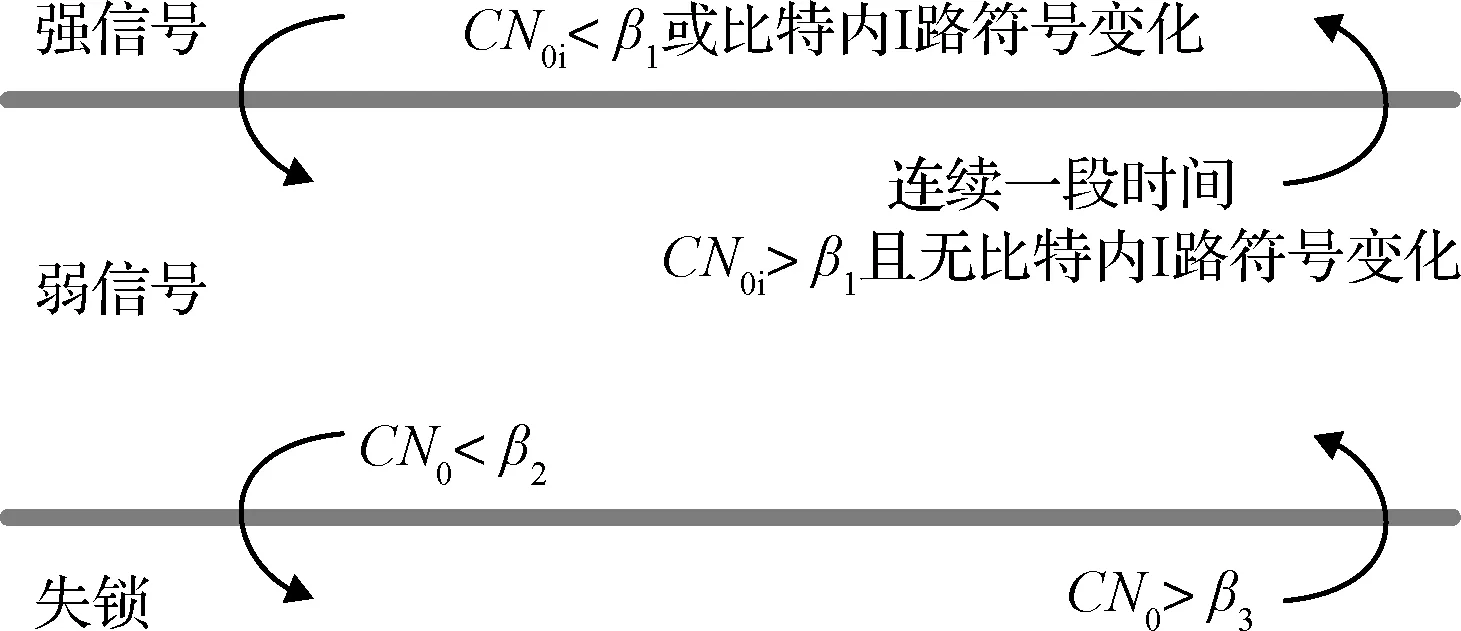
图7 信号强度判别策略示意图Fig.7 Illustration of signal intensity discrimination strategy
瞬时载噪比CN0i为20 ms I/Q数据利用窄带宽带功率比值法[15]计算的载噪比,其计算噪声较大,当数值较小时,表示信号可能不好,也可能是计算噪声造成的。本着宁可错判、不能漏判的原则,在强信号时若检测到瞬时载噪比低于阈值β1就转为弱信号。在强信号状态下,跟踪得到的导航电文比特一定是清晰的,在一个比特内I路数据的符号一定相同。如果检测到一个比特内I路数据符号发生变化,即使瞬时载噪比没有低于阈值,也应将强信号转为弱信号。当通道处在弱信号状态时,如果检测到连续一段时间瞬时载噪比都没有低于阈值β1且没有发生比特内符号变化,则重新判定为强信号。
平均载噪比CN0为1 s内瞬时载噪比的平均值,其计算噪声较小,反映一段时间的平均信号强度,时间上稍有滞后。弱信号时如果平均载噪比数值过低,则判定信号失锁,阈值设为β2。信号从失锁状态返回弱信号也由平均载噪比判断,阈值设为β3。为避免信号频繁在弱信号与失锁状态之间切换,β3应稍大于β2。
3 导航滤波器设计
3.1 状态方程
选取姿态失准角、速度误差、位置误差、接收机钟差等效距离误差、接收机钟频差等效速度误差、三轴陀螺仪零偏、三轴加速度计零偏作为状态变量:
X=[φx,φy,φz,δVN,δVE,δVD,δL,δλ,δh,δtr,
(1)
姿态失准角描述真实导航系(n)到计算导航系(n)′的旋转关系,在小角度条件下有如下近似形式:
(2)
由于系统使用MEMS惯导,其精度无法敏感地球自转角速度和有害加速度,所以利用惯导误差传播方程构建系统状态方程时,不必考虑包含地球自转角速度和有害加速度的项,则状态变量的微分方程简化为:
X+w=AX+w
(3)
(4)
(5)
(6)
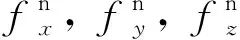
离散形式的状态方程为:
Xk+1=(I+AT)Xk+Twk=ΦXk+Twk
(7)
式中:T为滤波器更新周期。
3.2 量测方程
导航滤波器选取伪距误差、伪距率误差、载波相位差误差为量测量。
在一阶近似情况下,伪距误差与导航位置误差、钟差等效距离误差的关系为:
(8)
式中:ρI为使用惯导解算位置计算的天线相对卫星的距离,ρS为卫星信号处理测量的伪距,[ex,ey,ez]为ECEF(Earth-Centered Earth-Fixed)系下卫星指向接收机的视线单位矢量。∂(x,y,z)/∂(L,λ,h)为纬经高坐标到ECEF坐标的雅可比矩阵,表达式如下:
(9)
式中:sL,cL,sλ,cλ分别表示sinL,cosL,sinλ,cosλ。
在一阶近似情况下,伪距率误差与导航速度误差、钟频差等效速度误差的关系为:
(10)
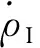
下面推导载波相位差误差与姿态失准角之间的关系。记当前惯导解算的姿态阵为:
(11)
真实的姿态阵为:
(12)
定义A天线指向B天线的位置矢量为系统的基线矢量,则基线矢量在地理系下表示为:
(13)
式中:l为基线长度,需预先测定。
真实的相位差表达式为:
(14)
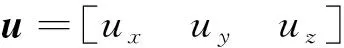
用惯导解算姿态计算的地理系下基线矢量为:
(15)
由此计算的相位差为:
(16)
式(14)与式(16)相减得到载波相位差误差:
δp=pI-pS=
[uyC31-uzC21uzC11-uxC31uxC21-uyC11]·
(17)
式(8)、式(10)和式(17)共同构成了深组合导航滤波器的量测关系。量测方程维数取决于信号强度判别,伪距、伪距率、相位差的量测个数分别记为n1,n2,n3。n1等于A天线强信号和弱信号通道个数的和,n2等于A天线强信号通道个数,n3等于跟踪相同卫星A,B天线都是强信号的通道个数。
实际应用中由于两个天线独立接收信号,信号所经过的线缆长度不会完全相同,所有通道相位差都存在相同的路径差引起的额外相位差。这个误差可以通过星间差分消除。另外,因为所有可见卫星均位于地平面以上,使用相位差确定姿态时,航向角测量精度高,而俯仰角测量精度较差。若直接使用相位差量测,相当于对航向角和俯仰角都做了直接量测,这个失准的俯仰角量测会影响正常的俯仰角估计。考虑将视线矢量投影到水平面上,投影后的相位差将不再包含俯仰信息。
原始视线矢量矩阵记为U,表达式为:
(18)
星间差分矩阵记为B,表达式为:
(19)
式中:1表示元素全是1的矩阵,I表示单位阵。B阵左乘U阵可以将所有卫星的视线矢量与第一颗卫星的视线矢量相减,以消除公共路径差。
完成星间差分后的视线矢量矩阵记为D,表达式为:
(20)
构造视线矢量水平投影矩阵F为:
(21)
F阵左乘D阵结果的最后一列都为0,使变换后的视线矢量没有z方向分量,以达到水平投影的效果。
执行星间差分和视线矢量水平投影的综合矩阵定义为:
J=FB
(22)
J阵的维数为(n3-2)×n3,使用J阵对导航滤波器量测方程的相位差部分做线性变换,得到最终滤波器所使用的量测方程。由于线性变换会使量测方程降两维,所以至少要观测到三颗卫星的相位差才能构造相位差量测方程。
下面将导航滤波器最终使用的量测量和量测矩阵进行总结:
(23)
(24)
(25)
(26)
(27)
3.3 导航滤波器运行流程
导航滤波器的运行流程如图8所示。滤波算法使用卡尔曼滤波。整个运行过程分为三部分,分别是惯性测量更新、卫星测量更新和导航误差修正。每次新的IMU数据到来时依次执行这三个部分。当由于遮挡没有卫星数据可获得时,只执行惯性测量更新,如图8中虚线所示。
对于图8中导航误差修正的第6步相位差整周误差修正部分,由于卫星信号的变化和可能跟踪到新的卫星,载波相位差的周跳现象时有发生,需要及时对相位差整周误差进行修正。修正方法为:使用当前姿态算出理论相位差,与测量的相位差相减,如果偏差的绝对值大于0.5,说明发生了周跳,进行整周修正,使偏差的绝对值小于0.5。
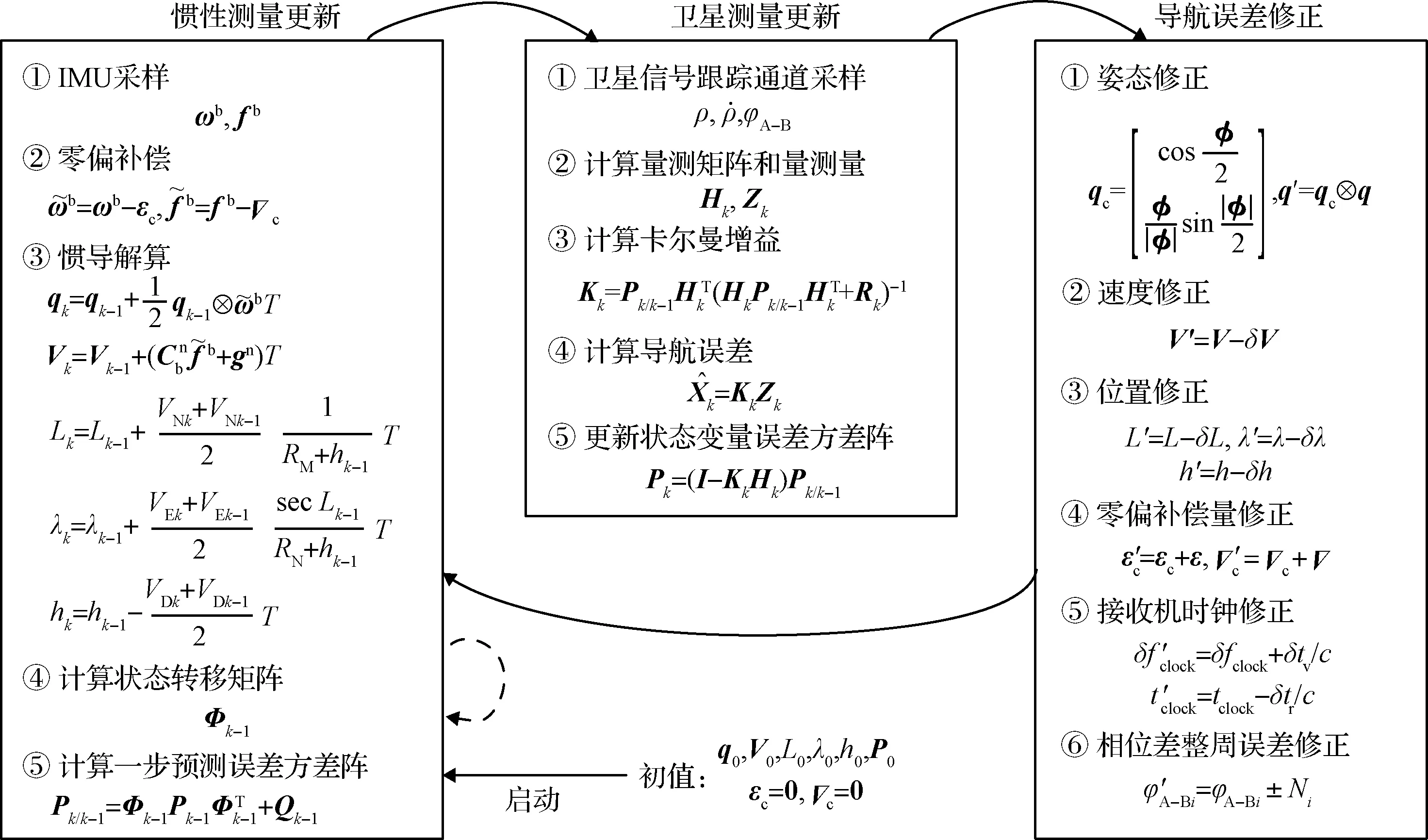
图8 导航滤波器运行流程图Fig.8 Flow chart of navigation filter
4 深组合导航系统试验验证
4.1 车载试验系统
双天线GPS/MEMS-INS深组合导航车载试验系统的配置方案如图9所示,系统实物如图10所示。
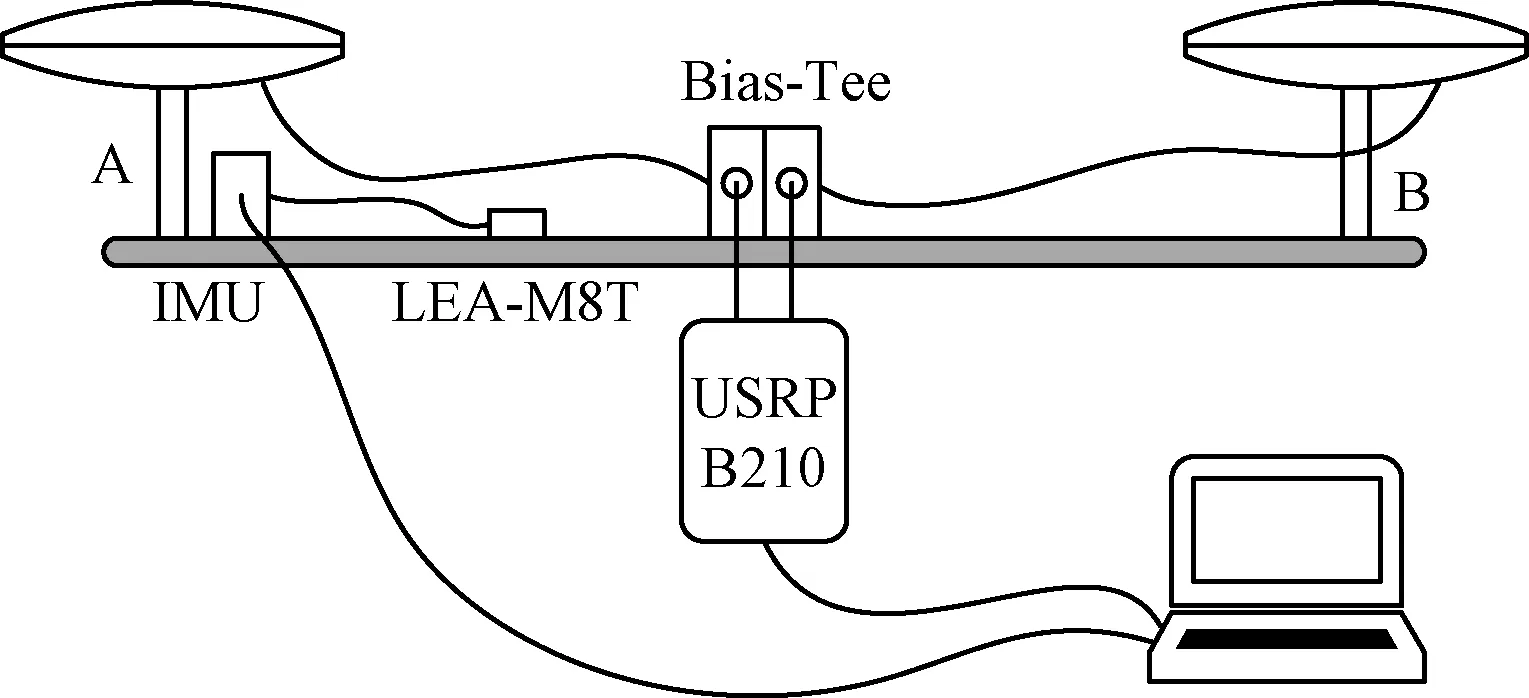
图9 深组合导航车载试验系统配置方案Fig.9 Deeply-coupled navigation vehicle-mounted test system scheme

图10 深组合导航车载试验系统实物图Fig.10 Deeply-coupled navigation vehicle-mounted test system equipment
系统包括两个GNSS天线、两个Bias-Tee天线供电模块、IMU模块、GNSS授时模块、通用软件无线电平台和笔记本计算机。关键器件的主要参数如表1~表4所示。
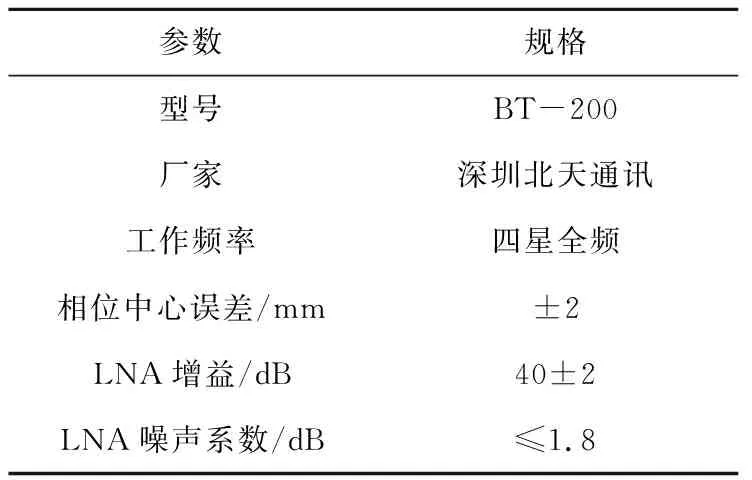
表1 GNSS天线主要参数Table 1 Main parameters of GNSS antenna
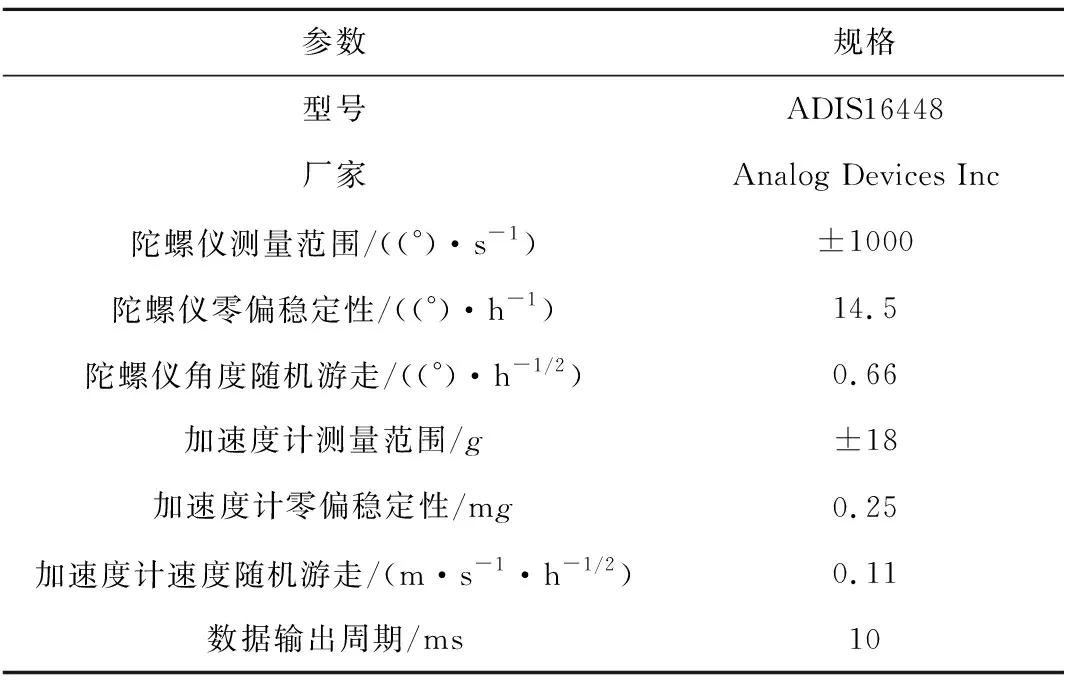
表2 IMU主要参数Table 2 Main parameters of IMU

表3 GNSS授时模块主要参数Table 3 Main parameters of GNSS timing module
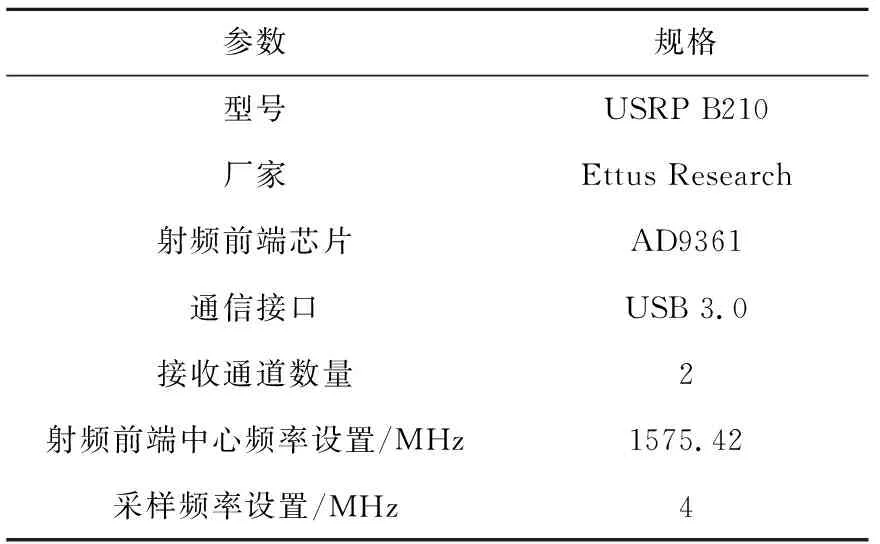
表4 通用软件无线电平台主要参数Table 4 Main parameters of universal software radio platform
两个天线安装在导轨的两端,基线长度设置为1.3 m。IMU靠近A天线安装,以减小IMU与A天线之间的杆臂误差,IMU的x轴与导轨纵轴平行。试验时进行数据采集和存储,离线执行深组合导航算法,算法程序使用MATLAB开发。实际系统中GPS信号和IMU数据是独立采集的,为了在算法执行时实现数据对齐,IMU数据采集电路中额外配置一个GNSS授时模块,在每一帧IMU数据输出时为其打上GPS时间戳。卫星信号跟踪的相干积分时间设置为1 ms,导航滤波器更新周期设置为10 ms。
4.2 试验结果分析
为验证深组合导航系统的性能,在城市环境中开展跑车试验,下面给出一组典型的试验结果。试验地点在哈尔滨工业大学附近,试验时间为2019年8月26日11时5分,信号采集时间10分钟,初始静止1分钟,用于系统初始化。图11为深组合导航的定位结果,图12、图13为局部放大图。车辆行驶路径中经过了楼群、树林、桥梁等复杂环境,深组合导航系统定位连续,没有出现因为卫星数量较少导致定位误差增大的情况,对短时信号中断有较强的适应能力。

图11 深组合导航系统定位轨迹Fig.11 Deeply-coupled navigation trajectory

图12 穿越桥梁时的导航局部放大图Fig.12 Enlarged view of trajectory while through bridge

图13 穿越密林时的导航局部放大图Fig.13 Enlarged view of trajectory while through jungle
图14、图15分别展示了静止和运动时单独GPS速度解算和深组合导航速度输出的对比。可以看出深组合导航降低速度噪声的效果非常明显,静止时速度噪声仅为0.01 m/s(3σ)。运动时深组合导航速度输出平滑,即使可见卫星数量较少而不能直接测速时也能保证连续输出(见图15中105 s~120 s)。
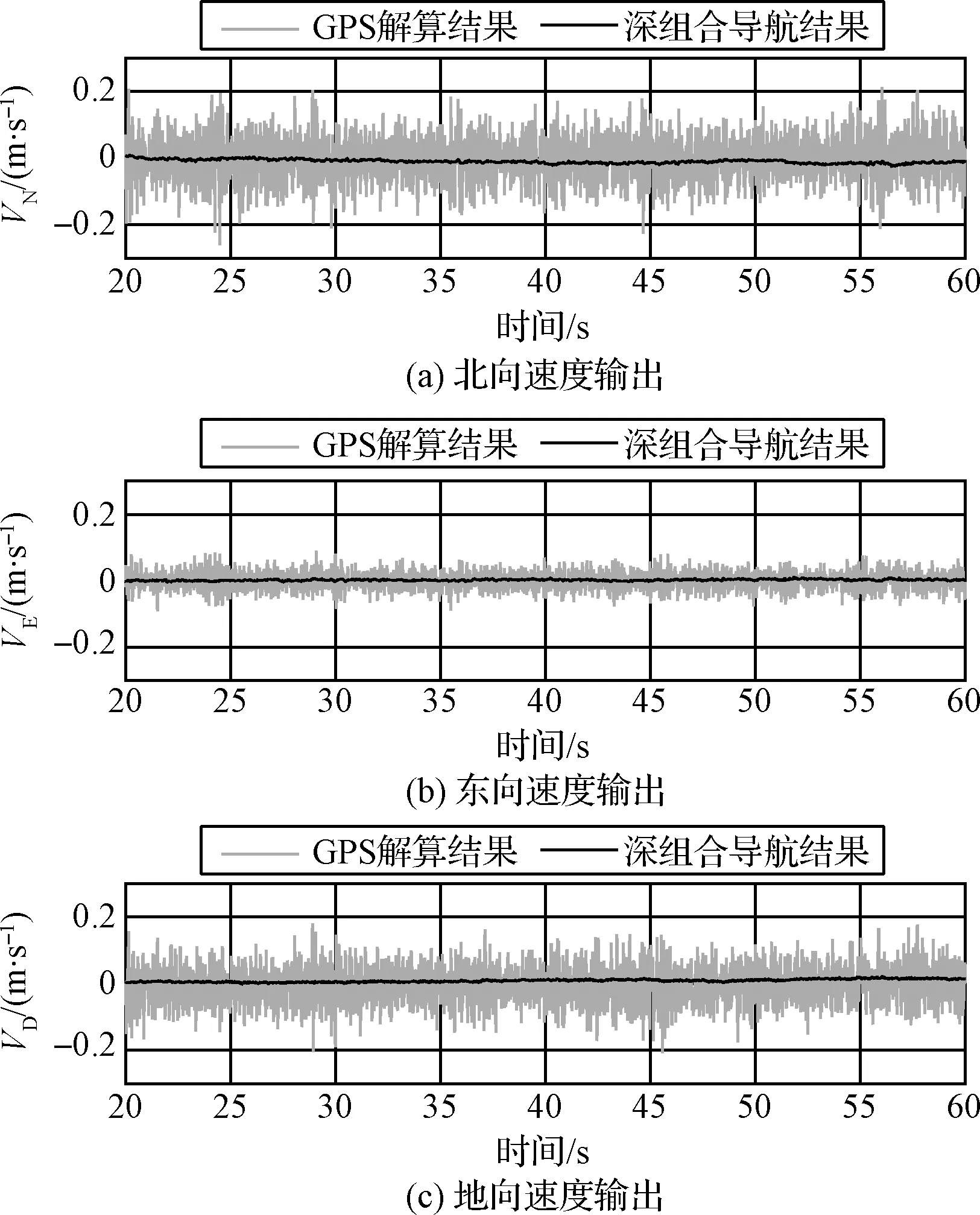
图14 静止时GPS与深组合速度输出对比图Fig.14 Comparison of velocity output between GPS and deeply-coupled navigation in the static
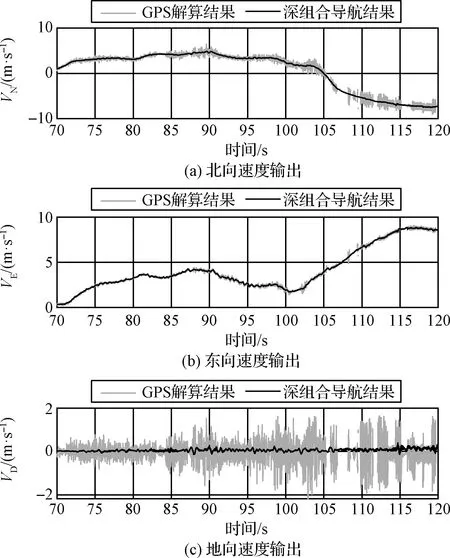
图15 运动时GPS与深组合速度输出对比图Fig.15 Comparison of velocity output between GPS and deeply-coupled navigation in the dynamic
图16、图17分别展示了静止和运动时GPS双天线相位差姿态解算和深组合导航姿态输出的对比。可以看出静止时相位差姿态解算赋予系统准确的航向初值,而且维持航向不发散。深组合导航的姿态噪声同样降得很低,静止时仅有0.05°(3σ)。组合后的俯仰角并没有跟随相位差姿态解算的俯仰角起伏(见图16(b)),说明导航滤波器相位差量测方程中视线矢量水平投影变换发挥了作用,屏蔽掉了俯仰量测。
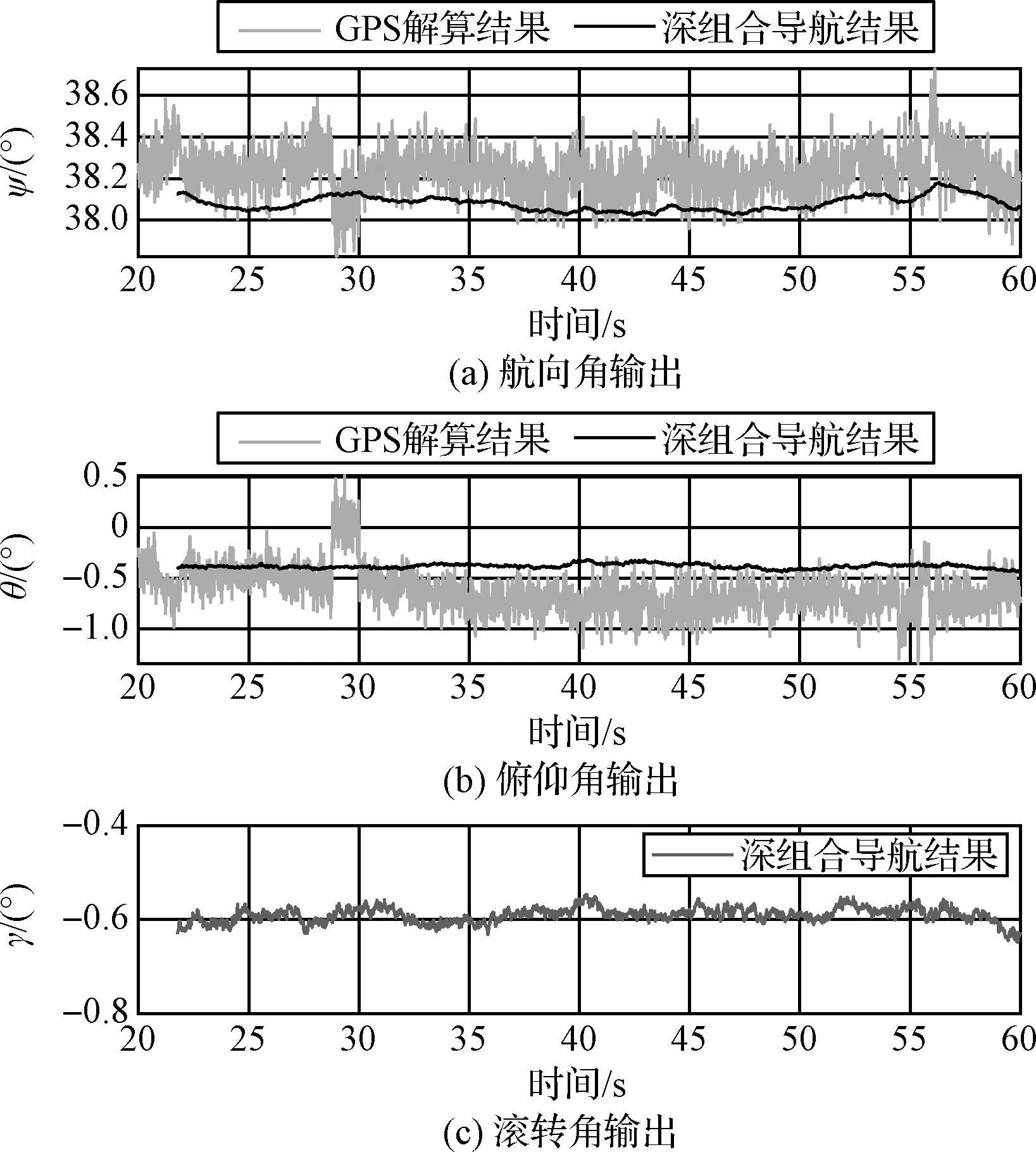
图16 静止时GPS与深组合姿态输出对比图Fig.16 Comparison of attitude output between GPS and deeply-coupled navigation in the static
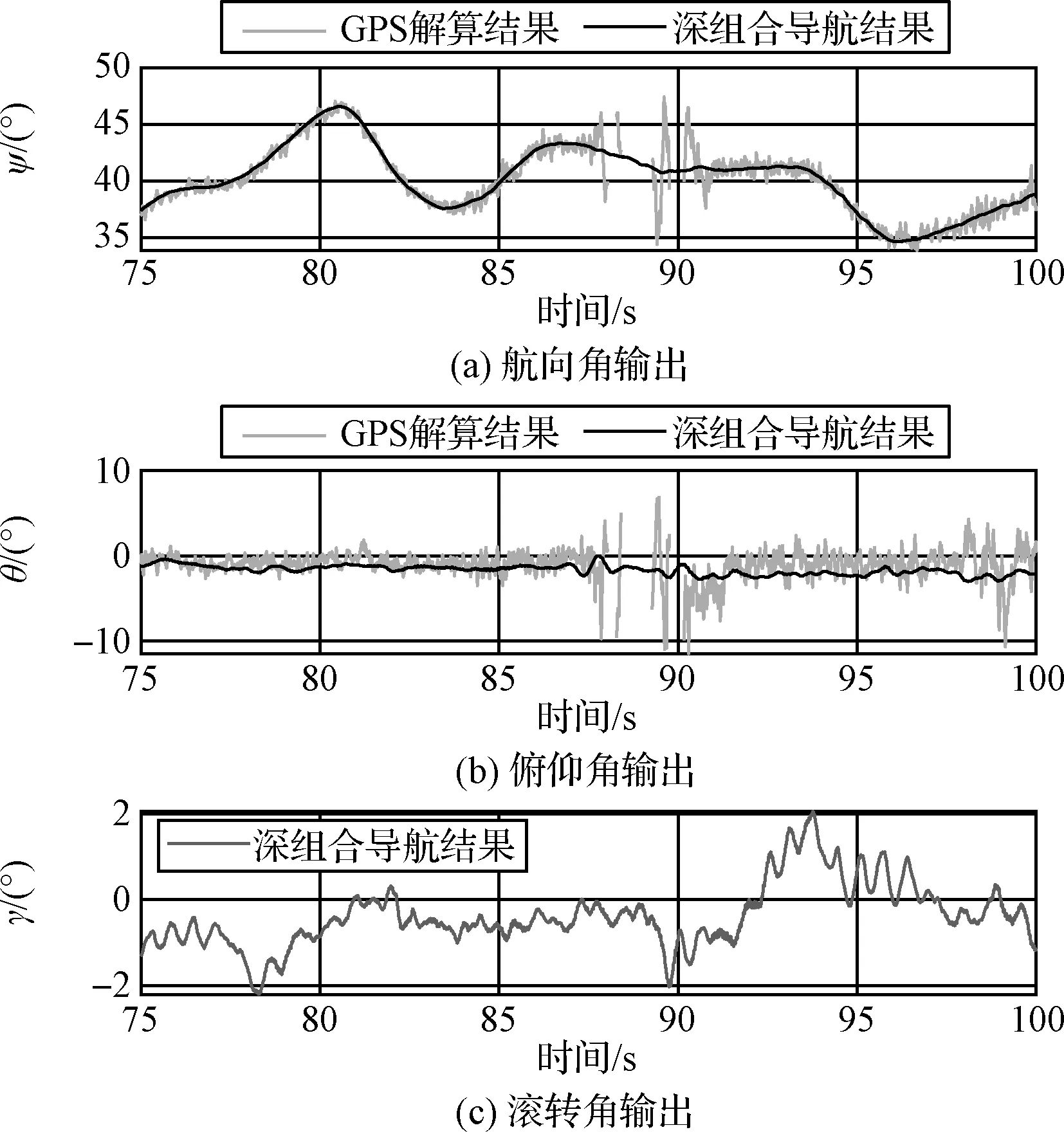
图17 运动时GPS与深组合姿态输出对比图Fig.17 Comparison of attitude output between GPS and deeply-coupled navigation in the dynamic
图18、图19分别展示了第22颗GPS卫星在不同信号状态下的载波频率跟踪结果和导航电文输出。395 s~398 s为强信号状态,导航电文清晰,由于锁相环独立运行,进行载波相位跟踪和频率测量,此时存在量测噪声。398 s~401 s为弱信号状态,导航电文输出存在波动,载波跟踪进入频率辅助跟踪模式,载波频率由导航滤波器提供。401 s~406 s信号被遮挡,跟踪环路失锁,无导航电文输出,载波频率仍由导航滤波器提供,虽然不能锁定相位,但可以保证频率正确,406 s信号恢复时能很快重新锁定。可以看出三种状态之间过渡平滑,实现了桥接中断信号的效果,所设计的跟踪环路可以适应信号强度的变化,提供了良好的载波跟踪性能。
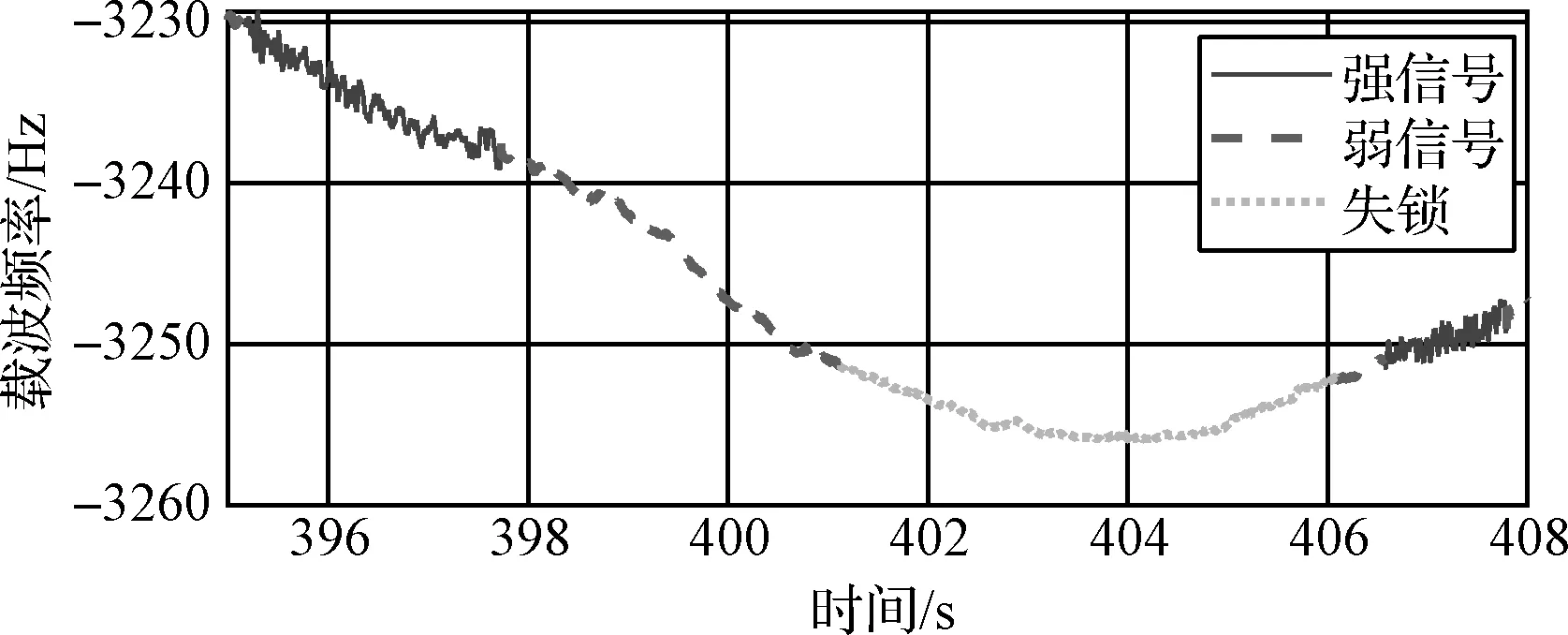
图18 第22颗GPS卫星载波频率跟踪曲线Fig.18 Carrier frequency tracking curve of NO.22 GPS satellite
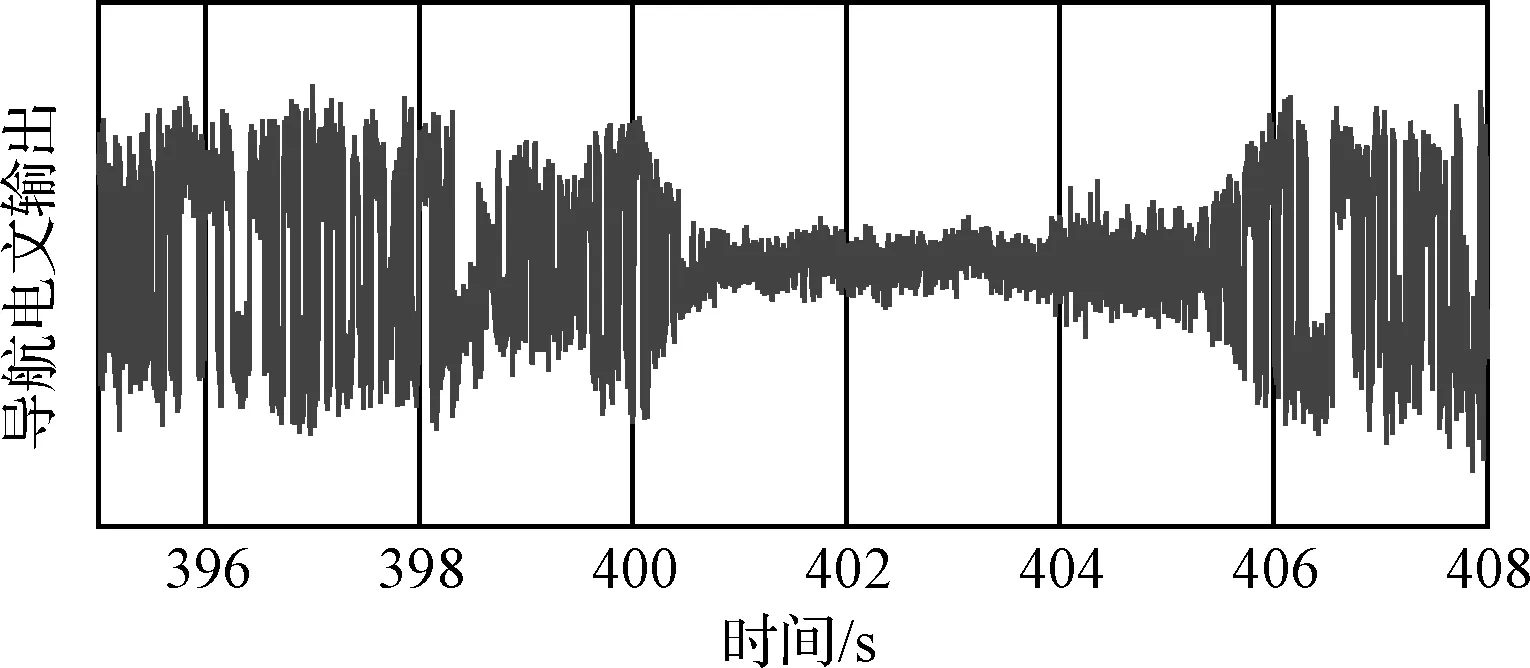
图19 第22颗GPS卫星导航电文输出Fig.19 Navigation data output of NO.22 GPS satellite
5 结 论
本文将双天线配置引入深组合导航系统,解决了MEMS惯导/卫星组合导航航向精度较差的问题。根据信号强度设计了三种跟踪结构,将质量好的卫星量测提供给导航滤波器完成导航修正,导航滤波器同时为弱信号通道提供跟踪辅助,所有通道联合处理,构成矢量跟踪环路,提高了跟踪精度,避免了信号失锁再恢复时的重捕获操作。在导航滤波器相位差量测方程设计中,采用视线矢量水平投影变换解决了相位差俯仰量测不准时的隔离问题。通过复杂城市环境中的车载导航试验,验证了所提出的矢量跟踪环路在面对信号衰减和中断时的连续跟踪能力,实现了高精度、稳定的导航输出。双天线GPS/MEMS深组合导航系统方案具有较强的工程实用价值。

