人工智能气动特性预测技术在火箭子级落区控制项目的应用

杜 涛，许晨舟，王国辉，宫宇昆，何 巍，牟 宇，李舟阳，沈 丹，程 兴，高家一，韩忠华

(1. 北京宇航系统工程研究所，北京 100076；2. 西北工业大学航空学院翼型、叶栅空气动力学重点实验室，西安 710072)

0 引 言

气动特性的预测是飞行器气动设计的核心工作之一。高超声速飞行器流动复杂，建立覆盖飞行包线的气动特性数据库通常需要开展规模庞大和复杂的风洞试验和计算流体力学(Computational fluid dynamics，CFD)计算，成为影响研制经费和进度的重要因素。

20世纪80年代之前，飞行器研制的气动特性预测主要依靠风洞试验，重要项目的试验量近乎天文数字，给研制成本和进度控制造成巨大压力。得益于计算机技术的发展，CFD进入工程领域，降低了研制对风洞试验的耗费。20世纪90年代后，一系列外界因素的改变促使工业部门意识到，需要发展更高效的气动数据库建立技术，降低研制成本并缩短周期。这成为飞行器设计领域活跃的研究方向。经过近30年的发展，已在下述三个方面取得长足进步。

1)预测中心从“数据”转移到“知识”

传统OFAT(One factor at a time)方法[1]，以“数据”为中心，试验规模与需求之间是线性关系。以现代试验设计(Modern design of experiments, MDOE)[2-3]为代表的新方法，以气动特性的“知识”和“关系”为中心，取代数据本身。当气动设计人员判断模型精度满足要求，风洞试验即可结束。兰利研究中心研究表明，采用MDOE策略，试验量减少了80%，风洞占用时间缩短了50%[2]。

2)气动数据融合技术

气动数据融合是指将不同来源、不同精度的气动数据，整合为一组高精度的气动数据集的方法。NASA在2014年发布的报告中曾指出[4]：“开展针对飞行试验、风洞试验和CFD方法的气动数据融合，可以快速、准确地预测飞行器气动特性，对指导风洞试验关键工况的选取具有重要意义。”

这一领域最有代表性的技术是可变精度方法[5](Variable fidelity model, VFM或Variable complexity model, VCM)。该方法最早是Dudley等[6]于1995年在NASA高速民用运输机研究计划中发展出来。Da Ronch等[7]运用变可信度代理模型方法，发展了一个用于飞行模拟的气动数据模型。Navarette等[8]提出采用基于径向基函数(RBFs)的神经网络方法实现不同来源气动数据的融合。2003年，在第二代LGBB(Langley Glide Back Booster)飞行器的气动数据库建立中，提供了一个数据融合技术工程实践范例。借助数据融合技术，在规定的一周时间内，高精度的粘性解仅占不到10%[9]。

3)人工智能预测技术

1985年，Tong[10]首次提出将人工智能技术应用于气动设计。随后，线性回归、支持向量机、贝叶斯模型和神经网络等机器学习算法得到发展，应用于气动数据预测[11-13]。机器学习，是指通过数据训练出能完成一定功能的模型，是实现人工智能的手段之一，也是目前最主流的人工智能实现方法。Marques等[14]采用监督学习的方法对超过1550个翼型的气动数据进行建模。Yilmaz等[15]利用深度卷积神经网络(CNN)从非结构的数据中对翼型的性能进行预测，预测结果的准确性超过80%。Bouhlel等[16]利用梯度增强的人工神经网络实现了亚、跨声速区翼型气动特性的快速预测。陈海等[17]以翼型图像作为输入，建立了CNN模型来预测翼型的气动系数。

但是，目前人工智能预测的研究工作，其气动数据规模较小，特性简单，缺少多维复杂数据的应用研究，更缺乏结果正确性的评估[18]。综合分析,技术成熟度仍处于实验室研究阶段，目前未见在工程项目设计应用的文献报道。

中国西昌等火箭发射场地处内陆腹地，火箭的一子级残骸往往坠落在内陆地区。随着社会的快速发展，落区人口日益密集，亟需采取措施降低发射任务对落区居民生产和生活的影响。对火箭残骸的落区控制早期采取预测残骸散布的被动控制[19]，当前以发展减少火箭残骸数量[20]或可控返回[21]的主动控制为主。由于内陆落区不具备回收条件，因此开展现役火箭的缩小落区范围研究更有现实意义。

本研究团队承担了现役运载火箭一子级落区精确控制的研制工作。在火箭一子级级间段增加四片栅格舵(外形见图1)，精确控制残骸落点。栅格舵的优点是可折叠，对上升飞行段的影响小，铰链力矩也小[22]，国内最早应用在CZ-2F的逃逸飞行器上增加稳定性[23]。在本项目上，栅格舵的工作马赫数范围扩大到高超声速，并参与控制和机动。不同于美国SpaceX公司的Falcon火箭一子级回收方案，有主发动机和姿控发动机的配合，本项目气动舵面操纵是姿态稳定和机动的唯一手段(如图2所示)，因而对气动特性预测的正确性要求更高，成为飞行成败的关键事项。

图1 火箭一子级落区控制的栅格舵方案示意图Fig.1 Illustration of grid fins in the rocket first stage landing area control project

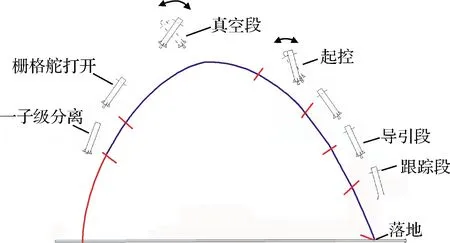
图2 火箭一子级落区控制飞行流程示意图Fig.2 Flight process of rocket first stage landing area control

由于栅格舵飞行中操纵状态较多，跨越马赫数范围广，建立设计气动数据库，需要开展规模巨大的风洞试验和数值仿真工作，对研制经费和进度构成挑战。为此，本项目团队探索在气动数据库建立上引入基于Kriging模型的机器学习方法，在解决多项技术难题并结合“人在回路”思想后，实现了机器学习方法处理多维复杂工程数据的能力。应用该方法在学习部分风洞试验及CFD仿真结果基础上，预测获得全部工况气动特性，加快研制进度。2019年7月26日，开展了搭载飞行试验，人工智能预测气动特性的方法获得了飞行验证。

本文首先简要介绍了所采用的基于人工智能技术的气动特性预测方法，然后给出了气动特性预测结果和飞行试验验证情况，最后对人工智能技术与气动设计进一步深入的结合和应用进行了探讨。

1 人工智能气动特性预测方法

1.1 机器学习算法介绍

针对气动数据分别来自风洞试验与CFD计算，具有不同可信度的特点，本文采用了基于加法标度的变可信度(VFM)模型和分层Kriging模型[24]的人工智能预测方法，下面分别介绍。

1)基于加法标度的VFM模型

基于加法标度的VFM模型是一种利用加法标度函数(桥函数)来近似高、低可信度数据修正量的变可信度模型[25-26]，即以低可信度模型为基础，通过加法标度的方式引入高可信度样本数据，辅助构建高可信度模型的近似模型。加法标度方法相比于乘法标度方法，能够使低可信度模型全局地逼近高可信度分析函数，鲁棒性更好[26]。

加法标度函数可以表示为：

γ(x)=yhf(x)-ylf(x)

(1)

(2)

随着高可信度样本点的增多，VFM模型中低可信度数据的影响应逐渐降低，使得最终模型的预估值能收敛到真实函数。

2)分层Kriging模型

韩忠华于2012年提出了分层Kriging模型(Hierarchical Kriging, HK)[24]，它是对传统Kriging模型理论[26,31]的进一步发展和完善。下面将对HK模型的算法和原理进行简要介绍。

首先，在带标签的低可信度训练样本集(Slf,yS,lf)基础上，建立低可信度的Kriging模型。由于低可信度的样本相对精度较差，因而可以将这里的标签认为是“伪标签”。所建立的低可信度Kriging模型预估值[24]可以表示为：

(3)

其中，

(4)

假设在高可信度样本点处存在静态随机过程：

(5)

Cov[Z(x),Z(x′)]=σ2R(x,x′)

(6)

与Kriging模型类似，可推得HK模型的均方误差为：

(7)

并需满足如下无偏估计的条件：

(8)

最小化均方误差(式(7))，即可获得最优的权重系数w。最终可以推导得到：

(9)

其中，

(10)

则HK模型的预估值可以表示为：

y(x)=β0ylf(x)+rT(x)R-1(yS-β0F)

(11)

其中，

β0=(FTR-1F)-1FTR-1yS

(12)

同时可以得到HK模型预估值的均方差为：

(13)

分层Kriging模型方法将低可信度模型的预估值直接作为全局趋势函数引入到高可信度模型的建模中，避免了高、低可信度交叉协方差的计算,提供了更合理的模型方差估计,降低了“相关矩阵”的维数，提高了建模效率。

本文首次尝试将机器学习模型应用于火箭一子级栅格舵复杂气动特性数据的获取。在新的应用环境下，场景复杂，对象规律性差。以图3跨声速段俯仰力矩特性为例，亚声速段在0°攻角附近是静稳定配平点，超声速变为不稳定配平点，规律复杂。而且飞行姿控设计对俯仰稳定性非常敏感，数据质量要求高。因此，必须改进现有方法，具备良好的鲁棒性与泛化能力，才能完成预测任务，下面将一一介绍。

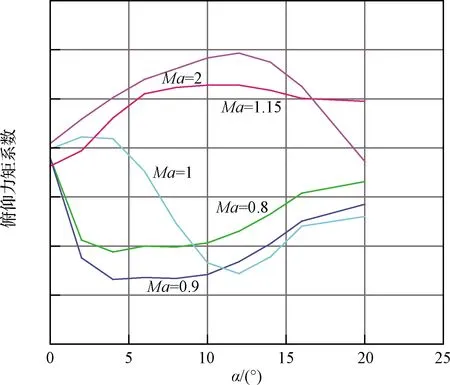
图3 火箭一子级带栅格舵外形跨声速段俯仰力矩特性Fig.3 Pitching moment characteristics of rocket first stage with grid fins in the transonic regime

1.2 机器学习模型相关函数的选择

Kriging建模过程中R和r的构造均涉及相关函数的选择和计算。而相关函数只与两个样本点之间的欧式距离有关。对于一个m维问题，一种流行的相关函数表示方式为：

(14)

式中:x,x′为两个不同的样本点位置；θ=[θ1,…,θm]T∈Rm为待定的模型超参数。

目前常见的相关函数模型有“高斯指数函数”和“三次样条函数”。“高斯指数函数”的表达式为：

(15)

这里pk代表相关函数光滑程度的各向异性参数[26]。pk=2时，相关函数无穷阶次可导。“三次样条函数”的表达式为：

(16)

其中,ξk=θk|xk-x′k|。该相关函数二阶可导，在光滑性和鲁棒性方面都表现较好。此外，还有一些基于径向基函数的相关函数，这类函数无超参数，如薄板样条函数。

本文选择了高斯指数函数、三次样条函数等相关函数，开展了预测对比研究，结果显示相关函数对预测结果有重要影响。对于气动设计优化问题，更倾向于选用表现更好的三次样条函数。而在气动特性建模预测问题上，两者的表现正好相反。

图4提供了采用三次样条函数预测得到的马赫数3升降舵引起俯仰力矩特性变化，不同曲线代表不同升降舵舵偏。预测结果发生了不同舵偏曲线交叉的现象，破坏了基本物理特性，预测完全失败。本文最终选择了高斯指数函数作为气动特性预测的相关函数。

图4 马赫数3的俯仰力矩预测结果(三次样条相关函数)Fig.4 AI predicted result of pitching moment coefficient of rocket first stage with Ma = 3.0(cubic spline)

两者的差异性表现可以给出一个理论解释。三次样条函数属于紧支撑性函数[32]，即当样本间的距离大到一定程度时，两者的相关性消失，这点与气动特性的全局相关性有物理上的冲突。而高斯指数函数，在pk=2时，无穷阶次可导，比三次样条函数更加光滑，可以很好地滤除气动数据中的噪声。高斯函数不具备紧支撑性，即使空间样本点相距甚远，也依然会考虑两者的相关性。而火箭一子级的气动特性预测显然属于全局性建模问题，因而采用高斯指数函数可以获得更好的结果[32]。

1.3 机器学习模型超参数的训练

在建立Kriging时，可以对模型的超参数θ进行训练，以提高机器学习的精度和灵活性。

对于分层Kriging模型，由于引入了低可信度样本，整个样本点集的似然函数为：

(17)

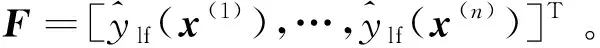
(18)

其中,n为高可信度样本点数。将式(18)代入式(17)，两边取对数，并去掉常数项后，对数似然函数可写为：

(19)

此时似然函数仅为超参数θ的函数，但θ并没有解析解，需要优化算法求解。本文采用的优化算法是结合信赖域方法的Hooke-Jeeves算法。根据以往的经验，高斯核函数超参数的优化范围选取区间[10-8θ0, 103θ0]。此外，研究还发现部分工况下固定超参数进行建模预测，有时要比超参数优化后的模型精度更高。

1.4 预测正确性的验证与确认

如何验证人工智能预测结果正确性，是应用者最为关心的问题，也是其在工程应用取得成功的关键性问题之一。飞行试验是确认预测正确性的最终极和最可信方式。但这是事后检验，对设计者充满风险，需要更加审慎。工程上更为关心的是在飞行试验前、数据产生和使用过程中的验证与确认。

目前，检验人工智能预测结果比较流行的方式是采用“交叉验证”方法，即屏蔽一小部分试验数据，将其设定为未知，然后用模型预测的数据与之进行比较。这一步对检验方法的正确性是必要的，第2.2节提供了对预测方法的交叉验证结果。但是对工程应用而言，“交叉验证”还不够。因为即便在屏蔽点获得了检验，也并不预示其他工况预测的必然正确。因此，还需要进一步的检验。

本项目引入了栅格舵气动特性的物理特性和规律对预测结果进行检验。气动数据并非不可预知的任意数据，它具有普遍性和通用性规律，这为预测的正确性提供了正面影响和保障。这些规律包括：1)数据间的逻辑关系;2)流动物理特征的规律;3)其他来源数据的比对关系;4)类似外形的数据特征。这当中有些规律和关系是强制性的。例如气动特性的极值应该出现在跨声速附近和高超声速条件下的Oswatitsch马赫数无关原则等。这些规律可以帮助研究人员检验数据的正确性。设计阶段产生的可靠数据，也可为正确性检验提供参考。事实上，该方法也被应用于风洞试验数据的正确性确认。

1.5 “人在回路”思想

在目前的技术条件下，纯粹的数学化计算机智能尚不能满足工程复杂环境应用的精度和鲁棒性要求。一些学者提出了“人在回路”模式，借助人工参与的形式，改进和优化预测结果[33]。文献[34]中指出：面向工程实际的优化方法需要引入“人机接口”以控制优化进程、引入判断与创新，其核心在于通过数据管理与可视化以及设计流程的自动化搭建，使设计师能够便捷地监控优化进程，再根据更新的输入重建优化进程。类似地，引入“物理学家”监督人工智能预测，在智能运算的前、后进行干预，一个纯粹的预测问题成为物理协助下的机器智能问题[35]。“人在回路”的设计流程反映在图5上。“物理学家”参与的核心是结果的检验(见第1.4节)。检验结果的反馈将同时作用于参与气动数据和预测方法上。开发人员有针对性调整参数设置、修正运行等方面的偏差和错误，确保在预期条件下运行，获得满意的结果。实现这一方法，需要“物理学家”掌握气动数据的物理规律和预测方法的规律。从某种意义上而言，“人在回路”设计有数据融合的影子。

图5 基于“人在回路”思想的设计流程Fig.5 Illustration of design process flow based on “man-in-loop” idea

2 栅格舵气动特性预测和验证

2.1 训练样本集介绍

预测对象是飞行器的六自由度气动特性，包括三个力和三个力矩。本项目研究中影响气动特性的要素包括：1)来流条件为马赫数(0～7)、高度(0～75 km)；2)飞行姿态为攻角、侧滑角和滚转角；3)舵偏状态为升降舵、副翼、方向舵舵偏角度。

在项目研制初期阶段，气动数据库的构建以CFD为主。但是由于栅格舵局部结构复杂，网格局部加密的规模巨大，计算效率较低。进入外形冻结阶段后，以风洞试验为主，辅以少量的CFD计算结果作为气动数据的训练集。风洞试验在中国航天气动研究院1.2 m尺寸的FD-12暂冲式风洞上开展(如图6所示)。不考虑耦合效应情况下，基本工况需要204个车次，滚转工况需要816个车次。需要几个月时间才能完成全部试验，不能满足项目紧张的进度要求。此外，高超声速段气动特性虽然对再入起控有重要影响，但单次试验费用较高。综合考虑进度和成本约束后大幅度压缩了高马赫数的试验工况。表1提供了项目开展的基本工况下俯仰通道的试验车次情况。根据姿控设计需要，每一马赫数应该开展-20°～ +20°范围不同升降舵舵偏的7个车次风洞试验。亚声速和跨声速条件的试验工况较全，马赫数4以上状态未开展试验。合计仅开展了所需工况的54%。

图6 火箭一子级带栅格舵模型在风洞中试验情况Fig.6 Experimental model of rocket first stage with grid fins installed in the wind tunnel

表1 俯仰特性风洞试验情况Table1 Fundamental state for wind tunnel experiment on pitching moment characteristics

2.2 预测方法的交叉检验

本节给出了预测方法的交叉检验结果。以升降舵舵偏操纵引起的俯仰力矩预测作为“交叉验证”方法算例。高可信度风洞试验数据分布在7个升降舵舵偏、10个马赫数和10个攻角的组合工况，共计492组；低可信度CFD计算数据共计96组。从492组高可信度样本里抽取了25组样本作为验证集(马赫数2的风洞试验抽取了-5°和-15°两个舵偏共20组数据，马赫数3的风洞试验随机抽取了5组)，剩余467组高可信度样本以及全部的低可信度样本用作模型训练集。验证集将被剔除机器学习的学习对象，仅作为检验点，检验预测结果的正确性。

定义如下指标来校验模型的预测精度：

1)相关系数r2：

(20)

2)标准均方根误差eNRMSE：

(21)

3)标准最大绝对误差eNMAE：

(22)

表2给出了采用交叉验证方法，模型的预测精度对比。从表2可以看出，相关系数r2非常接近1，均方根误差eNRMSE与最大绝对误差eNMAE接近0，表明预测结果具有相当高的精度。图7给出了预测结果与验证集的比较，预测结果均通过了未参与训练的检验点。

表2 机器学习方法的交叉检验结果Table 2 Cross validation of machine learning prediction method

图7 升降舵舵偏引起俯仰力矩预测结果的交叉检验Fig.7 Comparison of AI predicted result with validation experimental data of pitching moment coefficient caused by elevator deflection

2.3 预测结果

图8给出了升降舵操纵引起的法向力比较，工况为攻角20°和升降舵舵偏20°。机器学习预测结果通过了试验点，符合规律。

图8 升降舵舵偏引起法向力预测与试验值比较(α=20°)Fig.8 Comparison of AI predicted result with experimental data of normal force coefficient caused by elevator deflection (α=20°)

设计对俯仰力矩特性偏差的容忍度低，预测工作是本项的重点。同时开展了沿攻角和沿马赫数的双重检验，结果显示预测结果符合规律。图9提供了马赫数2时7个舵偏(-20°,-15°,-10°,-5°,0°,10°,20°)的试验和预测结果的比较，预测再现了试验结果。

图9 升降舵舵偏引起俯仰力矩预测与试验比较(Ma=2.0)Fig.9 Comparison of AI predicted result with experimental data of pitching moment coefficient caused by elevator deflection(Ma=2.0)

图10提供了马赫数3.0的俯仰力矩的机器学习结果。在该马赫数下，仅有0°和-20°舵偏两个车次的试验结果。机器学习结果完全重复了试验结果。其他工况结果符合物理规律。相邻马赫数2.0和3.5的试验结果均显示攻角20°附近升降舵20°的舵效为零。这一现象可以得到合理解释，升降舵的合成攻角较大，舵面易发生失速，舵面效率急剧下降。基于气动特性的常识，介于两者之间的马赫数3.0也应该存在这一现象。但是，马赫数3.0仅有的两个车次试验结果无法推导出该现象。不过机器学习预测出舵效为零的现象(见图10)。这就说明机器学习方法发现了相邻马赫数数据的物理规律，并在结果中予以体现。

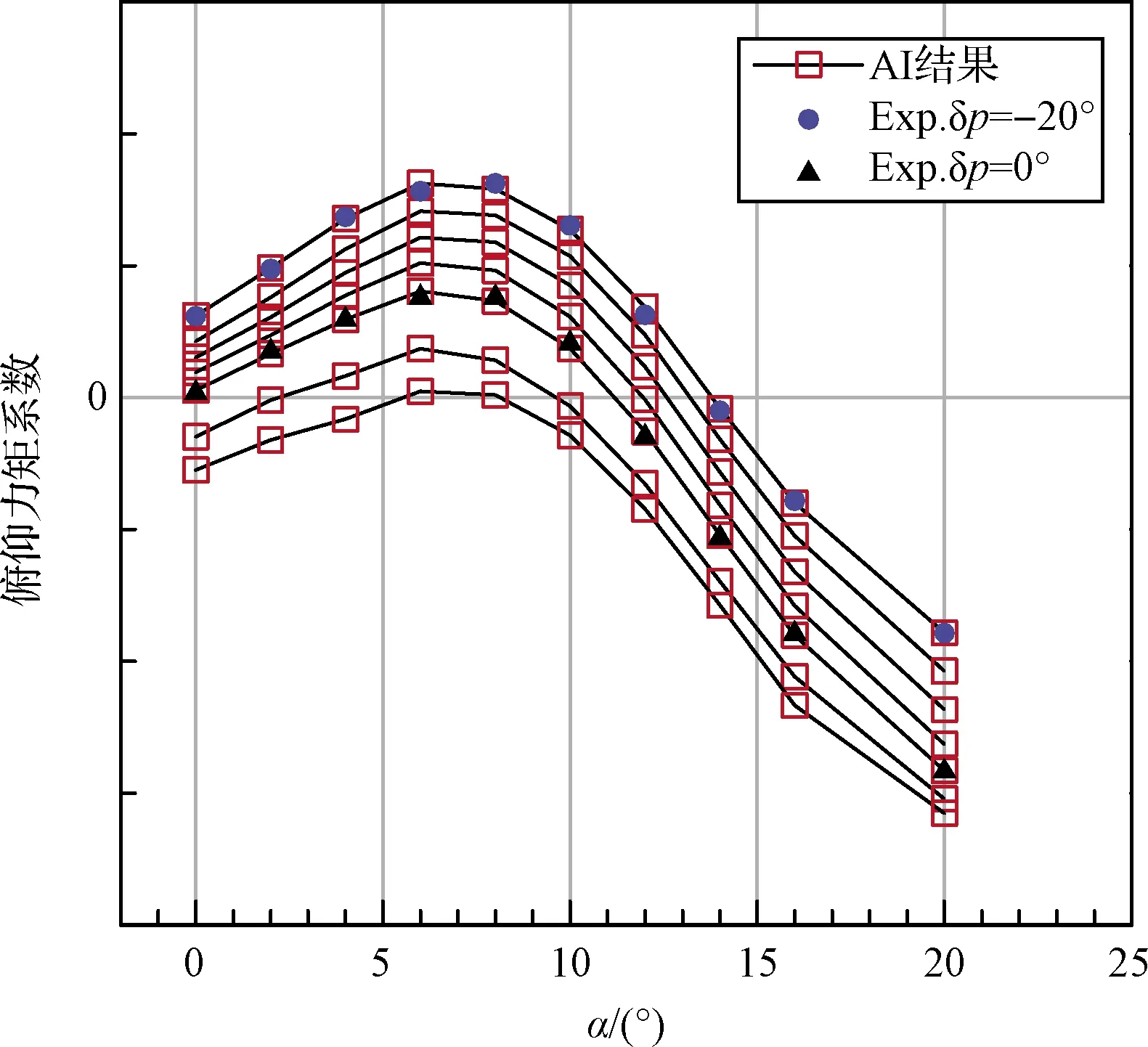
图10 升降舵舵偏引起的俯仰力矩预测结果与试验值比较(Ma=3.0)Fig.10 Comparison of AI predicted result with experimental data of pitching moment coefficient caused by elevator deflection(Ma=3.0)

图11和图12展示了机器学习提供的预测结果，其中马赫数4尚有一个试验车次，马赫数5未开展试验。图11同时提供了CFD计算结果来进行对比，结果表明预测与CFD结果一致性良好。

图11 升降舵舵偏引起的俯仰力矩预测结果与CFD计算结果、风洞试验值比较(Ma=4.0)Fig.11 Comparison of AI predicted result with CFD and experimental data of pitching moment coefficient caused by elevator deflection(Ma=4.0)

图12 升降舵舵偏引起的俯仰力矩预测结果(Ma=5.0)Fig.12 AI predicted result of pitching moment coefficient caused by elevator deflection (Ma=5.0)

图13～图15给出了5°侧滑角引起侧向力、偏航力矩和滚转力矩系数的预测结果比较。为了方便比较，仅提供了攻角为0°的结果,其他攻角的结果也类似。从图13～15可以看出，人工智能学习的结果与试验结果趋势一致,符合物理规律。

图13 侧滑角5°时侧向力系数的预测结果与试验值比较(α=0°)Fig.13 Comparison of AI predicted result with experimental data of lateral force coefficient when sideslip angle is 5°(α=0°)

图14 侧滑角5°时滚转力矩系数的预测结果与试验值比较(α=0°)Fig.14 Comparison of AI predicted result with experimental data of rolling moment coefficient when sideslip angle is 5°(α=0°)

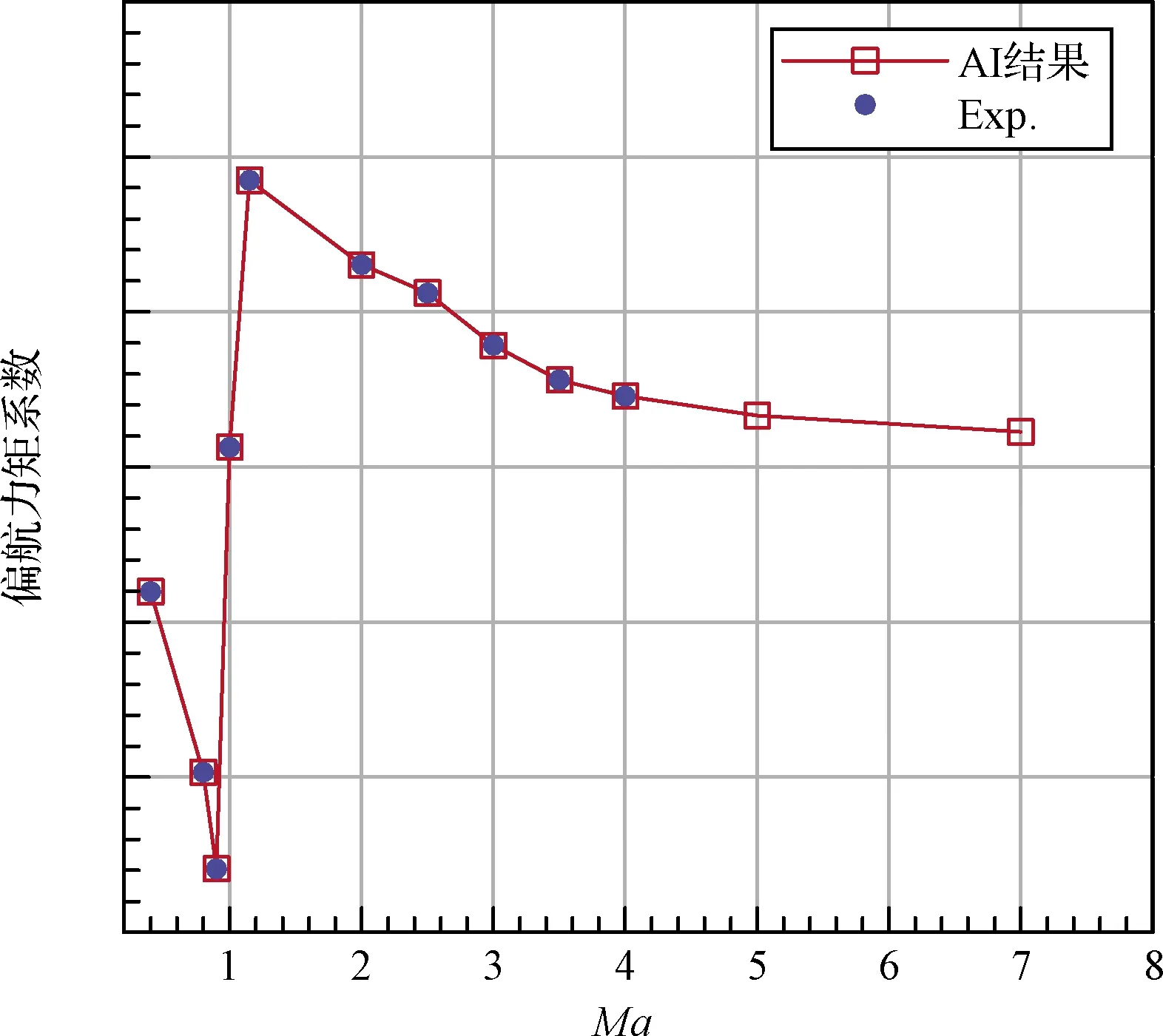
图15 侧滑角5°时偏航力矩系数的预测结果与试验值比较(α=0°)Fig.15 Comparison of AI predicted result with experimental data of yawing moment coefficient when sideslip angle is 5°(α=0°)

2.4 飞行试验验证

2019年7月26日，一子级落区控制项目参加发射搭载试验，落入预定落区，大幅度缩小落点范围，取得了成功(见图16)。箭上四片栅格舵上各自安装1台高清摄像头，对栅格舵在起飞、分离后展开和启控后工作的全过程进行图像记录(见图17)。图像显示飞行全程栅格舵工作情况良好。

图16 一子级落区控制搭载试验火箭起飞状态Fig.16 The take-off state of the test rocket in first stage landing area control project

图17 高清摄像头记录飞行试验中栅格舵展开的状态Fig.17 The unfolding state of grid fins in the flight test recorded by HD cameras

图18和图19提供了遥测获取的一子级再入大气层后的飞行攻角和栅格舵升降舵舵偏历程。从遥测结果可以看出，一子级残骸在进入大气层后，依靠摆动栅格舵的控制能力实现整个子级箭体的稳定和控制。子级再入大气后的姿态运动特性、栅格舵起控后的运动特性均与设计预测结果相当。跨声速段俯仰力矩稳定极性变化等多个典型气动事件均在遥测历程有所反映。

图18 一子级再入大气后飞行攻角遥测结果Fig.18 The angle of attack telemetry record for the first satge in reentry flight

图19 一子级再入大气后栅格舵升降舵舵偏遥测结果Fig.19 The grid fin elevator deflection angle telemetry record for the first satge in reentry flight

飞行试验结果表明，通过人工智能方法预测获得的火箭一子级再入过程宽马赫数剖面下的气动特性的正确性和有效性，依靠气动实现了再入的稳定和可控飞行。

3 人工智能技术在气动设计应用分级的探讨

人工智能预测技术虽然在本项目的应用获得了飞行验证，但还是应该清醒认识到该项技术还处于初级阶段。未来会有从“低”到“高”的发展过程，智能的内涵和应用结合点也会不断深化和拓展。

过度拔高无助于人工智能技术的发展。同时，也应该摒弃怀疑和观望的态度，主动促进融合。技术发展和应用将是一个不断相互促进的过程。目前需要解决的是，如何增加设计师对智能技术的信任度，解决办法是对人工智能的技术特征进行划分和定位，以便于开发人员和应用人员正确理解不同阶段人工智能的能力和应用范围，避免期望过高或是应用错位。

目前在汽车自动驾驶领域，对自动驾驶技术的划分提供了一个良好的思路和范例。自动驾驶分为L 0～L 5[36]，依次为无自动驾驶、驾驶员辅助、部分自动驾驶、特定条件下自动驾驶、高度自动驾驶以及完全自动驾驶，既促进了自动驾驶技术的良性发展，也避免了用户错误应用。

为推动人工智能与气动设计的结合，根据已有的实践，并参考自动驾驶的分级原则，本文提出人工智能在气动设计应用的级别划分。将有助于气动设计人员正确评估智能技术，建立理性预期，既不提出超越技术阶段的目标，也不错失智能技术提升设计的帮助。应用等级分为A0,A1,A2,A3,A4和A5六个等级。A0是完全无智能技术介入，A5级别最高，可实现完全智能化和自动化。划分标准和特征见表3。参考分类，可以评估本项目的应用定义为A2级别，具备初级智能，但还需要人工监督。

表3 人工智能技术在气动设计应用的分级和标准Table 3 Classification and standard of application of artificial intelligence technology in aerodynamic design

4 结 论

在我国首次开展的火箭一子级落区控制项目上，设计团队发展和应用了基于VFM和分层Kriging模型的气动特性人工智能预测方法，实现了低成本和快速建立一子级栅格舵外形的气动特性数据库，解决了由于进度和经费原因，项目风洞试验工况不足问题。相关结论如下：

1)本文发展的基于VFM与分层Kriging模型的人工智能的气动特性预测方法，达到了通过部分风洞试验结果和CFD结果，去预测完全覆盖飞行的工况，从而快速和低成本地构建出一子级栅格舵外形气动特性数据库，降低设计对风洞试验的需求。

2)2019年7月26日飞行搭载试验取得成功，结果表明，本文方法预测的气动特性结果正确、可靠,说明该方法能够满足飞行设计的需求。

3)Kriging模型相关函数选择和模型超参数训练对预测结果具有重要影响。采用高斯指数函数的预测效果优于三次样条函数，这与应用于优化设计的结论有所不同。

4)通过引入“人在回路”技术，成为基于Kriging模型的气动数据预测的有益补充，降低了数据驱动预测建模风险。

5)结合应用需求，本文提出了人工智能技术在气动设计应用的分级概念和标准，以推动人工智能技术与气动设计的融合，为正确理解各阶段人工智能的能力和应用范围提供参考。

后续将继续探索气动特性预测与人工智能的深度融合，改进现有基于数据模型的预测方法，发展基于物理的预测准则与方法，进一步提升气动特性预测的智能化水平。