一道概率统计问题的探究与推广

广东省珠海市第一中学(519000) 赖嘉辉

概率统计是高中数学的一个很重要的分支,它与我们的生活息息相关.从它的题目特点来看,很好地考察了学生对实际问题的分析,建模,求解的能力,也能很好地体现出学生的核心素养能力.从近几年的高考命题上,更加注重了对能力和素养的考查,试题设计上增加了应用性和能力推理性.本文对一道概率统计题进行了探究与推广,并在推广过程中得到一个有趣的结论.

问题数字1,2,3,4,5 任意排成一列,如果数字k 恰好在第k 个位置上,则称有一个巧合.

(1)求巧合数ξ 的分布列.

(2)求巧合数ξ 的期望.

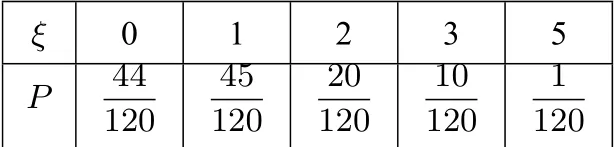
ξ 0 1 2 3 5 P 44 120 45 120 20 120 10 120 1 120

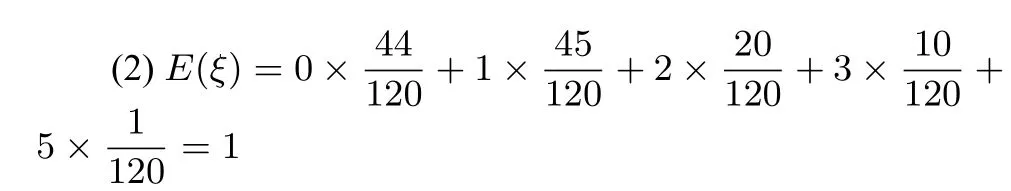
上述问题是高中概率统计的一道练习题,此题研究的是5 个数字情况,属于中等难度的题目.我们可以把它推广到n个的情况,而且我们还在推广的过程中发现了一个有趣的结论.

问题的推广数字1,2,···,n 任意排成一列,如果数字k 恰好在第k 个位置上,则称有一个巧合.

(1)求巧合数ξ 的分布列.

(2)求巧合数ξ 的期望.

问题分析依题意可得,巧合数ξ 可能的取值为0,1,2,···,n - 2,n.当巧合数为m 时,即有m 个数字恰好在它自己对应的位置上,而另外的n-m 个数字都不能它在自己的位置上,为了完成问题的推广,我们需引入以下的概念.

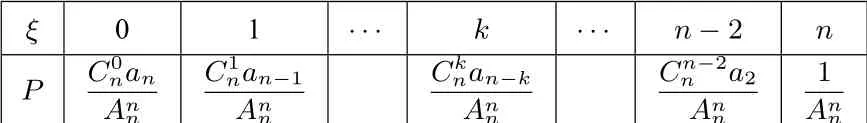
ξ 0 1···k ···n-2 n P C0nan Ann C1nan-1 Ann Cknan-k Ann Cn-2n a2 Ann 1 Ann

(2)根据引理1 和2,巧合数的数学期望为从上述推广的结论我们可以发现,不管数字n 是多少,我们都可以计算出巧合数的数学期望为1.同时,我们可以这样理解:当数字n 很小时,某一个数字能在它自己位置上的概率就大了,但是巧合数ξ 的最大值就小了;而数字n 很大时,某一个数字能在它自己位置上的概率就小了,但是巧合数ξ 的最大值就变大了,从数学期望本身的定义来看,巧合数的数学期望为1 还是很有可能的.