2020年广州市一模圆锥曲线试题研究*
鞠火旺 (广东省中山纪念中学 528454)
1 问题的提出
解析几何中的定点问题是一类综合性问题,在直线与圆锥曲线的位置关系中,当直线满足一定的约束条件时,直线往往会过定点或者形成包络线[1]. 下面是2020年广州市一模文、理科数学第20题,两题的题干和第(1)问相同,只是第(2)问略有不同. 本文对该问题进行探究与推广.
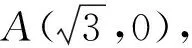
(1)求曲线C的方程.
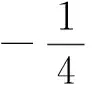

图1 图2
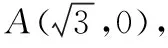
(1)求曲线C的方程.
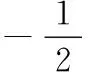
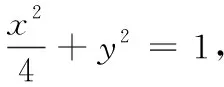
2 探究与推广
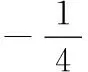
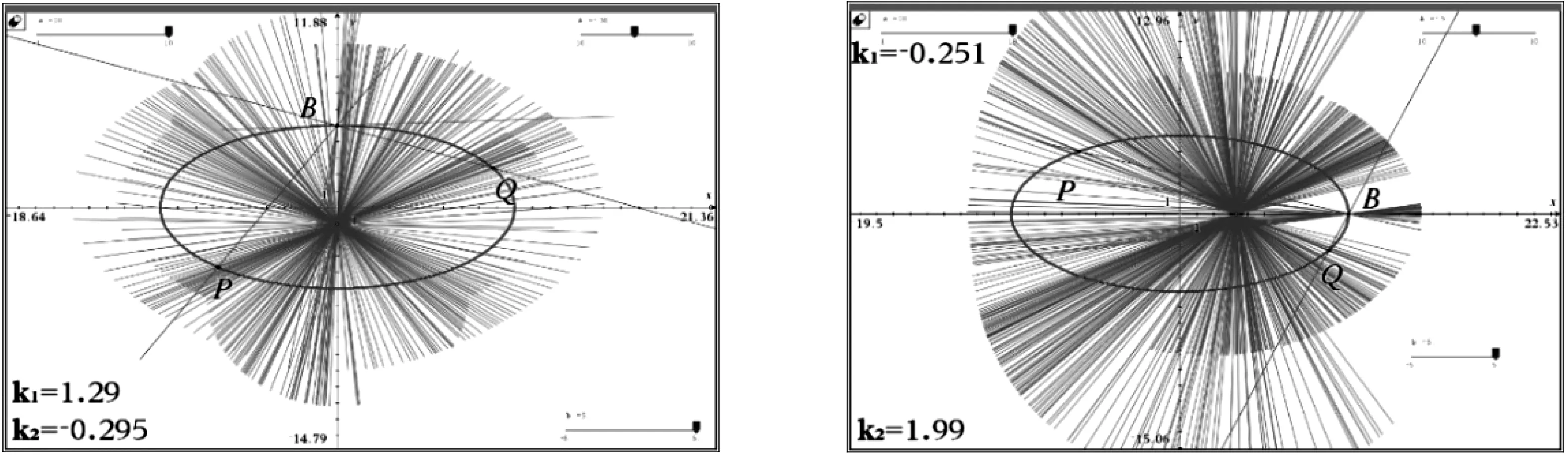
图3 图4
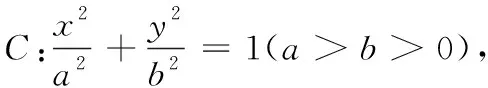
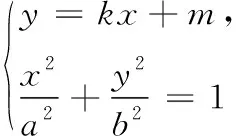
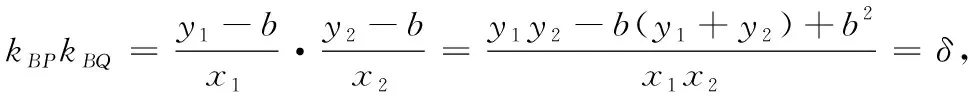
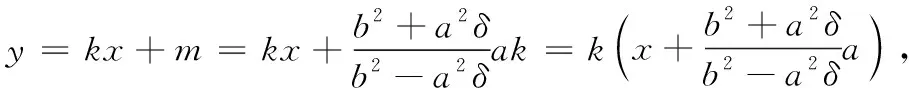
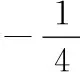
3 进一步推广
由上可知,过椭圆的上顶点或右顶点作两直线,当两直线的斜率之积为定值时,所张的弦恒过定点. 那么过椭圆上任意一点作两条直线与椭圆相交(图5),当这两条直线的斜率之积为定值时,过两交点的直线还会过定点吗?经过探索发现直线的确过定点(图6),于是我们得到如下结论.
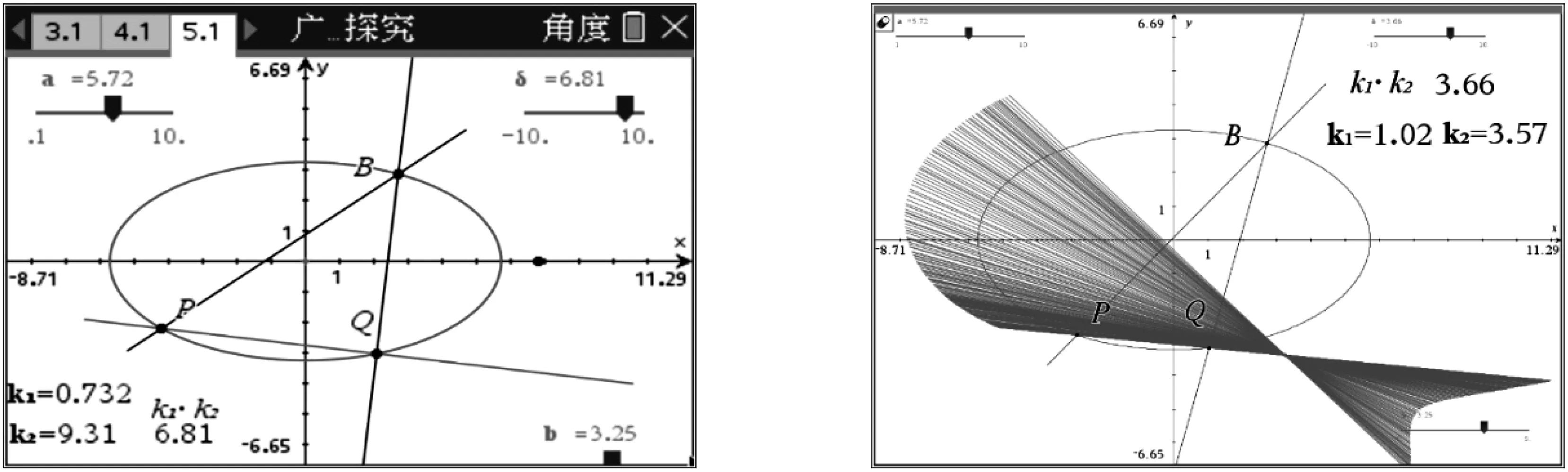
图5 图6
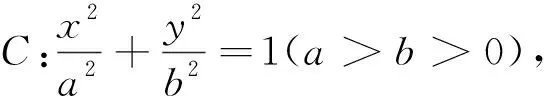
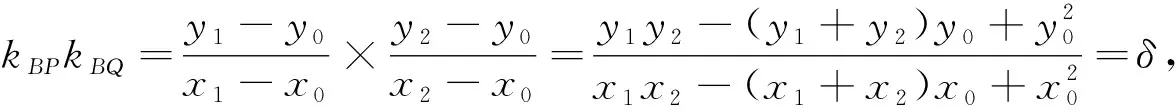

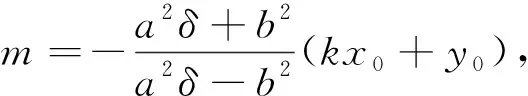
上述结论中的点B是椭圆上的任意一点. 自然有追问:若点B为椭圆内或椭圆外任意一点,过点B作两条直线BP,BQ,它们分别与椭圆相交于点P和Q(图7),且BP和BQ的斜率之积为δ,那么直线l是否仍然过定点?经过实验发现动直线l形成包络线(图8). 为了方便研究,不妨将点B取在坐标原点,这并不影响问题的本质.

图7 图8
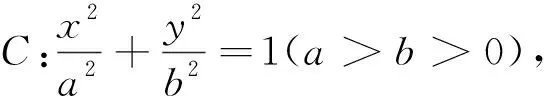
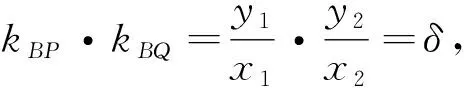
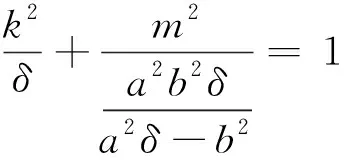
(ⅰ)当δ<0且δ≠-1时,包络线为椭圆. 其中, 当δ∈(-∞,-1)时焦点在y轴上;当δ∈(-1,0)时焦点在x轴上.
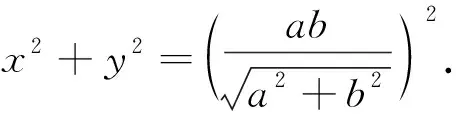
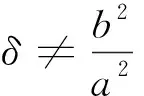
4 推广与统一
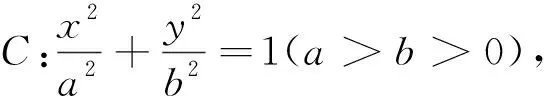
结论证明的过程中会涉及大量的符号运算,具体的证明我们留给感兴趣的读者. 我们借助TI图形计算器的CAS运算功能,求出了一个关于x,y的二元四次方程,该方程的形式过于复杂,本文就不再给出具体的表达式了.
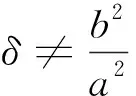
图9和图10给出的是当λ≠1且δ<0时包络线对应的图象,由于当点B在椭圆内部时,直线BP和BQ与椭圆共产生了四个交点,故图9和图10叠合在一起才是完整的包络线图象.
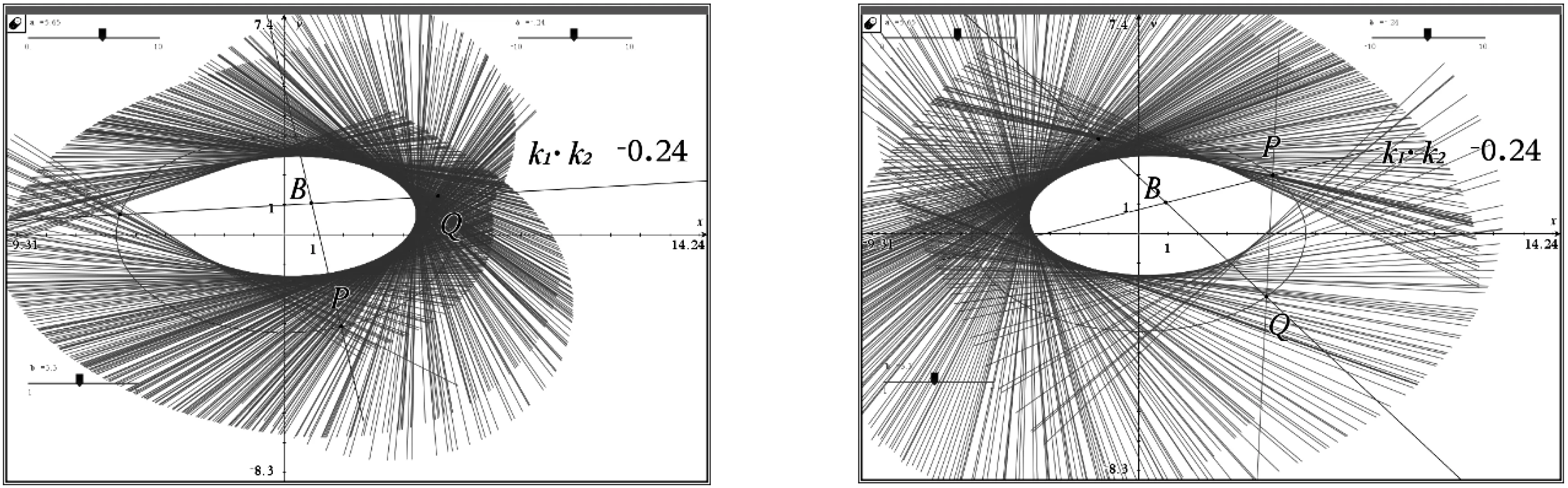
图9 图10
至此,我们已经对这道试题及其推广形式有了比较完整的认识. 在双曲线中也有类似的结果,限于篇幅我们就不再赘述了.

