着力一题多解 引领学生思考——以一道高三质检题为例

蔡海涛 (福建省莆田第二中学 351131)

本文以一道高三质检题为例，提供了多种解题思路，兼顾了解题的通性通法和特殊解答技巧，引领学生进行解题反思，归纳并提炼解题思想和方法，同时在解题教学层面进行了深入思考，旨在培养学生的数学核心素养．

1 试题呈现

(2020年莆田市高三第三次质检·理21)设函数f(x)=xlnx，g(x)=aex(a∈R)．

(1)若曲线y=f(x)在x=1处的切线也与曲线y=g(x)相切，求a的值．

(2)设函数G(x)=f(x)-g(x)存在两个极值点． ①求a的取值范围；②当ae2≥2时，证明：G(x)<0．

2 解法探究

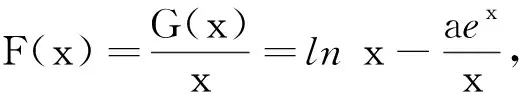
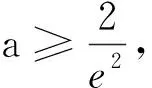
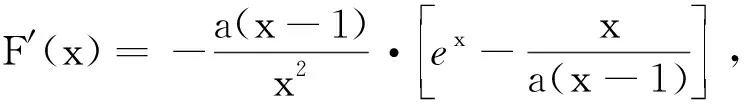
因为H(m)·H(2)≤0，所以H(x)存在唯一零点x0∈(1,2)， 故F(x)有唯一的极大值点x0∈(1,2)．

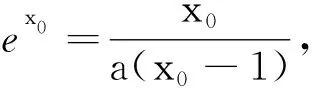
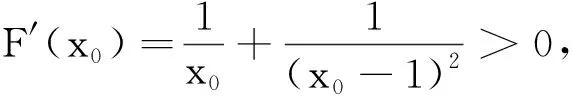
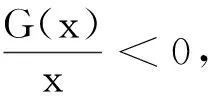
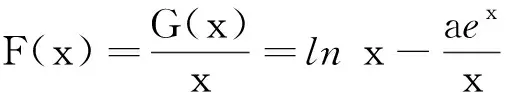
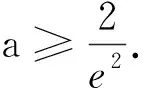
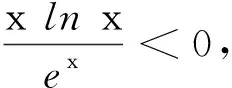
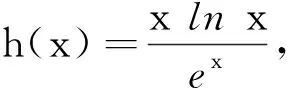
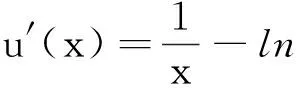
又u′(x)在区间[1,+∞)上单调递减，故u′(x)≤u′(1)=0，即u(x)在[1,+∞)上为减函数．

又u(2)=1-ln 2>0，u(3)=1-2 ln 3<0，故存在x0∈(2,3)，使得h′(x0)=0，即lnx0+1-x0lnx0=0 (*)．

于是当10，h(x)为增函数；当x>x0时，h′(x0)<0，h(x)为减函数．

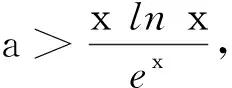
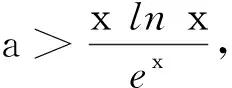
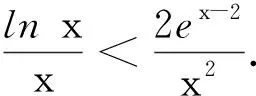
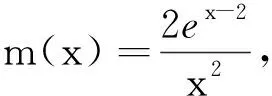
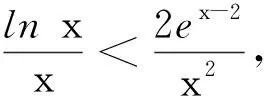
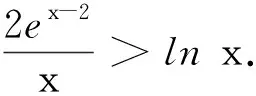
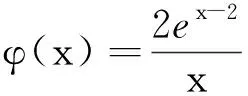
3 变式拓展

(1)求函数f(x)的单调区间；

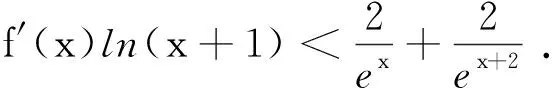
解(1)函数f(x)在(0,1)上单调递增，在(1,+∞)上单调递减. (过程略)

令g(x)=1-x-xlnx，则g′(x)=-1-(lnx+1)=-2-lnx．

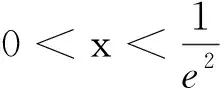
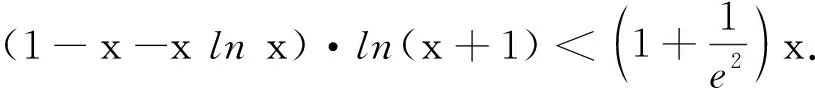
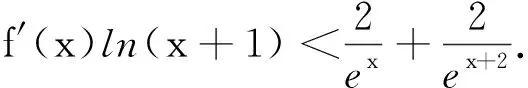
评注对于含有lnx与ex型的超越函数，具体解决时须根据这两类函数的特点，挖掘结构特征，灵活变形，脑中有“形”，特别注意重要不等式lnx≤x-1⟺ex≥x+1的合理代换．

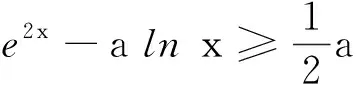
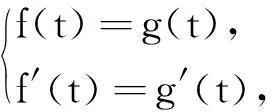
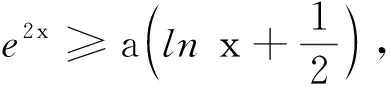
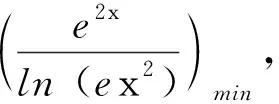
4 教学启示

(1)对解题教学的思考

在解题教学中，教师常常采用一题多解，让学生从多种思维角度来思考问题，既要重视通性通法又要关注特法巧解，解后引导学生对解题方法进行归纳，在数学思想上进行引领． 指数、对数组合型的函数不等式问题，常用的解题方法有三种：一是指数、对数分离并向易于求最值的常用函数转化；二是利用放缩消掉指数函数或对数函数之一，再进行处理；三是隐零点法． 对于具体问题，可根据函数特征具体分析，选择合适的方法求解．

解题教学中还可常常对问题进行变式，让学生通过 “变中发现不变”来学习抽象化并通过“以不变应万变”来学习公理化，以此来解决数学教学中的核心问题——“抽象化”和“公理化”． 基于突出数学本质的解题教学，不应局限在解题方法的展示，更应引导学生在课内、课外注重知识背后的数学思想、方法的贯通，注重形、数之间的结合，引导学生进行学习内容逻辑线索的梳理，强化在数学实践活动中综合运用数学知识的能力，从不同角度思考问题，由此建立起知识体系，从而能以“一览众山小”的姿态来看待数学问题．

(2)精选例题，聚焦高考

教师讲解模拟卷的典型试题，应聚焦高考试题，进行高考试题对点链接，引导学生学会归纳试题的共性，学会应对试题的创新变化，看破迷雾，提升抓住问题本质的能力． 高考压轴题都具有一定的创新性，解题教学中教师应努力培养学生的发散思维，拓宽学生的视角. 只有这样才能让学生做到“以不变应万变”，笑傲考场．

(3)引领学生深度思考

解题教学中教师应引领学生进行深度思考，引导学生从不同视角、不同方向进行观察、类比、联想，引领学生思考一题多解、一题多变、多题一解、多解归一；思考答题难点是什么，为什么不会，这种解法能否推广；思考这道题还可以得到哪些结论，条件结论能否互换. 通过思考，获取问题的内在联系，关注学习内容的有机整合. 注重知识学习的批判理解,着意学习过程的建构反思,重视学习的迁移运用和问题解决，从而领悟数学之美，提升核心素养．