反例在初中几何教学中的应用:以全等三角形的判定为例*

哈尔滨工业大学(深圳)实验学校(518000) 王 伟

香港教育大学数学与资讯科技学系 张侨平

广东省深圳市教育科学研究院(518000) 林 炜

1 引言

在演绎几何的教学当中,要说明一个结论的正确,需要严谨的证明;而要说明一个结论不正确,只需要举出一个反例即可. 这两个方面都体现了数学学科言必有据的特点. 不过在教学中,我们比较多重视前者,着重培养学生演绎推理的能力. 对于举反例,我们强调的不多. 或许有人以为,举反例只是用特殊实例取代一般的正规证明,比不上严谨的演绎推理. 事实上,在数学教学中,教师若能根据教学实际需要,举出合适的反例, 不仅有助于帮助学生加深对概念的理解,也能培养学生的批判性思考能力[1]. 本文以初中平面几何中全等三角形这一课题为例,来说明反例在数学教学中的运用及其教学意义.

全等三角形的学习是初中生从直观认识几何图形到学会根据几何图形的性质进行演绎推理的重要阶段,也是学生第一次比较全面的学习几何的演绎证明. 在义务教育数学课程标准(2011 版)中,关于全等三角形的知识要求为:“理解全等三角形的概念,能识别全等三角形中的对应边、对应角;掌握基本事实: 两边及其夹角相等的两个三角形全等. 掌握基本事实: 两角及其夹边分别相等的两个三角形全等;掌握基本事实: 三边分别相等的两个三角形全等;证明定理: 两角分别相等且其中一组等角的对边相等的两个三角形全等以及探索并掌握判定直角三角形全等的‘斜边,直角边’定理”[2]. 对于这些基本要求,不同的教师会通过不同的方式教学,帮助学生将这些知识熟练掌握. 而考验学生是否真正掌握和理解,他们能否接受这一系列的“基本事实”和“定理”等,从而在解题中熟练运用,一般都只能通过考试来检验.

从全等三角形概念入手,两个“完全重合”的三角形是全等三角形,因此,全等三角形除了对应角相等,对应边相等之外,跟图形的度量相关的三角形的对应的周长和面积也相等.以北师大版(2015)初中数学为例[3],在常规的教学中,学生要理解全等三角形如上的所有性质,一开始是通过将两个三角形进行重合的具体动手操作活动,形成对图形全等的直观认识,这样的直观操作后,学生也比较容易理解“全等”的概念. 接下来就是逐一介绍两个三角形全等的种种性质,包括对应角相等,对应边相等(对应周长,对应面积,对应边上的中线,对应边上的高,对应角的角平分线在之前的全等图形章节中进行了学习). 最后,也是比较重要的一部分,需要向学生教授全等三角形的判定条件,满足怎样的条件两个三角形才是“全等三角形”. 再利用尺规作图验证全等的几个判定条件,最后利用全等三角形测量距离进行实际的运用,学生就算是学完了全等形这一课题. 整个教学流程图可见图1.

图1

顺着这样的教学路径,知识逻辑是清楚的,学生也应明白的. 然而在实际教学的反馈中,我们发现对于两个三角形的全等判定定理的理解,学生掌握的情况并不是太好. 虽然学生也能够熟练的将这五种判定方法“倒背如流”,但在具体运用中,会“张冠李戴”,将全等三角形的性质与判定弄混乱.特别在遇到条件复杂时(判定条件需要自行寻找判断),不知如何选择策略. 究其原因,主要还是因为学生对于判定定理的学习基本停留在表层的再现和复述,没有深入理解几种判定条件的实质,做不到灵活地分析和运用.

如果纵观整个三角形全等的判定学习过程,我们会发现整个教学内容基本都是集中在对应角和对应边的寻求(无论教科书还是练习题都是如此),留给学生自行探索和思考的空间都还比较窄. 那么,能否通过逆向思维,帮助学生更好的理解和掌握三角形的判定定理. 逆向的思考,对学生来说并非第一次经历. 我们知道,定理的逆命题不一定成立,如“两直线平行,内错角相等”的逆命题“内错角相等,两直线平行”是成立的;而对于“对顶角相等”这个定理的逆命题“相等的角是对顶角”是不成立的. 因此,对于全等三角形如上的性质定理,学生也可以通过思考它们的逆命题是否成立,从而探究出全等三角形的判定: 只有哪些条件,并不能证明三角形全等.

2 全等三角形反例教学的过程

2.1 性质定理“全等三角形对应角相等”的逆命题:“对应角相等的两个三角形全等”不一定成立. 具体分析过程如下:

(1)只有一组对应角相等的两个三角形不全等. 通过展示出下图的几组反例均可证明该逆命题不成立, 如图2 中反例,两组三角形中均有对应相等的∠A, 但这两组三角形也明显不全等.

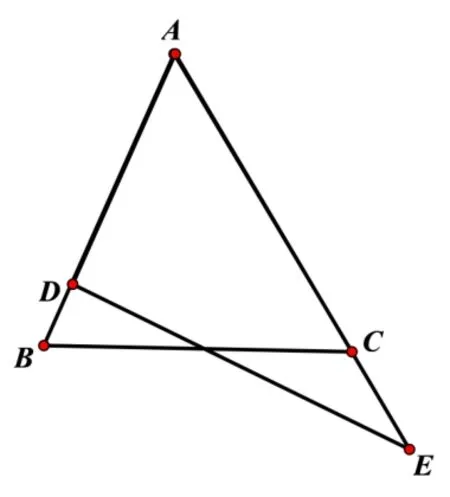
图2

(2)两组对应角相等的两个三角形不全等. 通过三角形的内角和等于180°易知这两个三角形的第三组内角一定也对应相等,通过展示如图3 的反例可以得到证明. ΔABC和ΔAB′C′中,B′C′//BC, 因此两个三角形三组对应角都相等,但这两个三角形并不全等. (课堂上,教师也可以借助于教师用的大直角三角板和学生用的小直角三角板举反例)

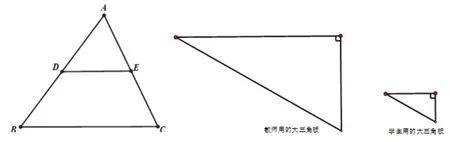
图3

2.2 性质定理“全等三角形对应边相等”的逆命题:“对应边相等的两个三角形全等”不一定成立. 具体分析过程如下:

(1)一组对应边相等的两个三角形不一定全等. 教学中可以展示如图4 的反例: 在几何画板中,构造ΔABC和空间内不同于点A的另一点A′,连接A′B,A′C,构造出ΔA′BC,ΔABC和ΔA′BC有共同的BC边, 但由于A′的随意性,这两个三角形不一定全等. (当且仅当A′为点A关于BC对称点是,两个三角形全等)

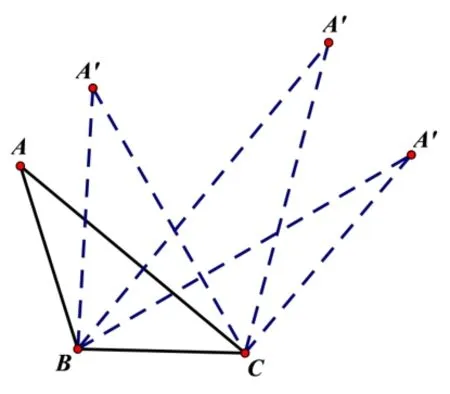
图4

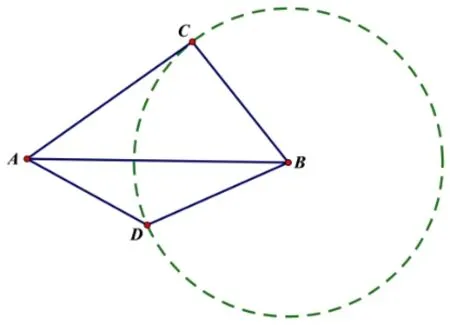
图5

(2)两组对应边相等的两个三角形也不一定全等,展示如图5 反例: 在几何画板中,构造线段AB,以点B为圆心,任意长为半径作圆,在圆周上任取两点C、D,因为圆周上的点到圆心的距离相等, 即BC=BD. 连接AC,AD, 构造ΔABC与ΔABD, 这两个三角形中,AB=AB(公共边) ,BC=BD,满足两个对应边相等,但明显这两个三角形不一定全等. (当且仅当C、D关于AB对称时,两个三角形全等)

(3)三组对应边相等的两个三角形一定全等(SSS).这是一个正确的结论,是教科书中的“基本事实”. 三条边的长度确定了,这个三角形也就唯一确定,这也可以用来说明“三角形稳定性”. 教材的后续内容“用尺规作图做三角形”一节中,会验证这个结论的正确性.

在上述对性质定理的“逆命题”的学习研究中,通过恰当的反例,使学生能够对“在两个三角形中,如果只有一组,两组对应角(对应边)相等两个三角形都不一定全等”这些不成立的逆命题的理解更为清晰明确,也对“三条对应边两个三角形全等”(SSS)的结论有了更直观的认识.

2.3 对应边和对应角组合相等的两个三角形不一定全等. 具体分析如下:

(1)一组对应边,一组对应角相等的两个三角形不一定全等. 可以通过如图6 反例得到证明: 在几何画板中, 构造ΔABC, 在AC边上任取不与A、C重合的点D, 连接BD,构造ΔABD,在这两个三角形中,∠A= ∠A(公共角),AB=AB(公共边),但明显这样的两个三角形不全等.

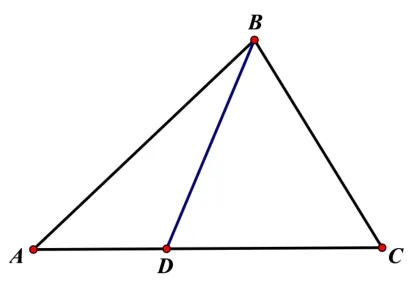
图6

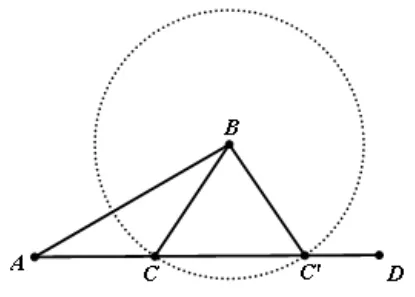
图7

(2) 一组对应边, 两组对应角相等的两个三角形一定全等. 这种组合分两种情况, 两组对应角和它们的夹边相等(ASA)和两组对应角和一个角的对边相等(AAS),其中ASA 这种情况也是作为“基本事实”无须证明,而第二种情况(AAS),则可以通过三角形内角和,将其转化为ASA 得以证明.

(3)两组对应边,一组对应角相等的两个三角形不一定全等. 这种组合同样分两种情况. 其中两组对应边相等,并且这两条对应边所夹的角也对应相等的两个三角形全等(SAS),作为“基本事实”无需证明;另一个两组对应边相等,并且其中一条对应边所对的角也对应相等的两个三角形不一定全等(SSA),可借助如下的反例进行说明.

在几何画板中,构造∠A,在∠A的一边上固定一点B,以点B为圆心,大于点B到角的另一边AD的距离为半径作圆,交AD边与点C与C′,这样就构造了ΔABC和ΔABC′,这两个三角形中,AB=AB(公共边),BC=BC′(圆周上的点到圆心的距离相等),但明显这两个三角形不全等.

至此,教材中关于三角形全等的判定定理戛然而止,学生的逆向思维也到此被强硬的暂停. 其实,全等三角形的性质定理中,“全等三角形对应周长相等”,“全等三角形对应面积相等”这两个的逆命题是否成立,教材中并没有进行探究思考. 那么,能不能延续学生平行线性质定理学习的思维,继续用反例来研究“全等三角形对应周长相等”,“全等三角形对应面积相等”这两个逆定理是否成立. 接下来,我们继续对这两个性质定理的逆命题进行探讨研究:

2.4 性质定理“全等三角形周长相等”的逆命题: 周长相等的两个三角形全等不一定成立. 具体分析如下:

两个三角形的周长相等,只要三边之和相等即可,三边的长度可以不一样,这样的三角形肯定不全等. 如图8 的反例,两个三角形的三边长分别为3,4,5,和5,5,2,周长均为12,这两个三角形不全等.

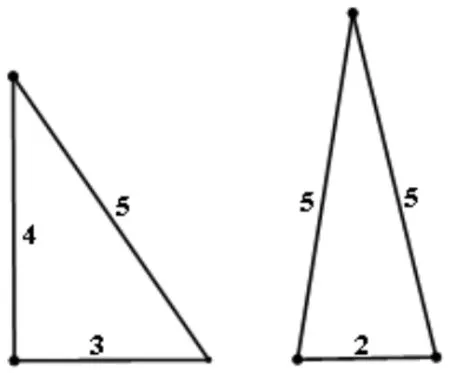
图8

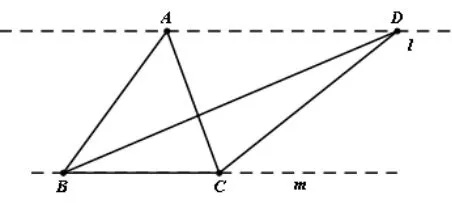
图9

2.5 性质定理“全等三角形面积相等”的逆定理:“面积相等两个三角形全等”不一定成立. 具体分析如下:

三角形的面积是三角形的底和高乘积的一半,只要底和高的乘积一定,面积一定相等,但乘积一定的底和高可以不相同. 如图9 的反例,在几何画板中,构造ΔABC,过点A做BC边的平行线,在平行线上任取不同于点A的点D,连接BD,BC,构造ΔABD,由于平行线间的距离相等,即这两个三角形的高相同,BC=BC(公共边),因此这两个三角形的面积相同,但明显这两个三角形不全等.

2.6 命题:“周长和面积都相等的两个三角形全等”不一定成立. 具体分析如下:

(1)固定周长,调整面积.

在几何画板中, 先构造等边三角形ABC, 若边长为a,ΔABC的周长为3a,在BC边所在的直线上确定一点C′.做C′关于线段BC中点O的对称点B′,若C′O=x,分别以B′,C′为圆心,以(1.5a-x)为半径画圆,两圆的交点记为A′,在C′点的移动过程中,始终保持A′C′=A′B′= 1.5a-x,所以ΔA′B′C′的周长为2x+(1.5a-x)+(1.5a-x)=3a,因此ΔABC和ΔA′B′C′的周长相等. 在C′点的移动过程中,ΔA′B′C′的面积也是从0 变大到变到0,在这个过程中,一定存在一个定点C′′,使得ΔA′B′C′与ΔA′′B′′C′′的面积相等,但很明显这两个三角形不全等.

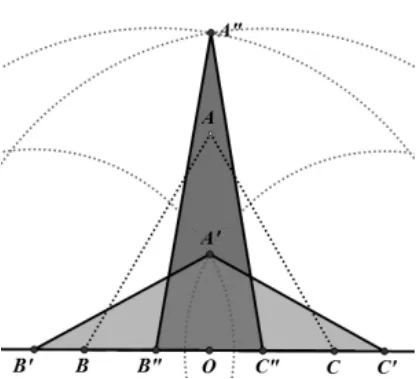
图10

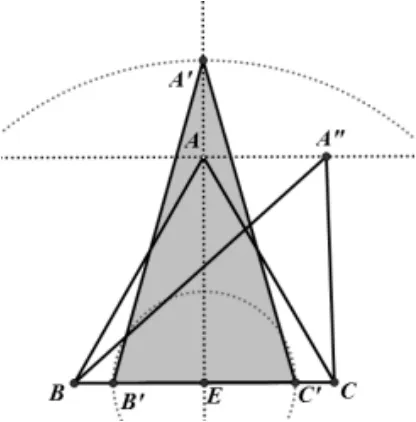
图11

(2)固定面积,调整周长.

在几何画板中,先构造等边三角形ABC,假设边长为a,E为BC边上的中点,设定参数k,以E为圆心,以为半径画圆,交BC所在的直线与B′,C′,则B′C′=k·a(放大或缩小均可). 以E为圆心,k·AE为半径画圆,交AE所在的直线于点A′,连接A′B′,A′C′,容易计算出ΔABC的面积与ΔA′B′C′的面积相等. 利用几何画板度量出ΔA′B′C′的周长.

过点A做BC边的平行线, 在其上取一点A′′, 因为ΔABC和ΔA′′BC等底等高,所以这两个三角形面积相等.可以通过几何画板度量出ΔA′′BC的周长. 拖动A′′在平行线上运动,ΔA′′BC的周长也随之发生变化,在这个过程中,一定存在某一点,使得ΔA′′BC和ΔA′B′C′的周长相等. 但是,很明显这两个三角形不全等.

因此,通过如上两个反例,周长和面积相等的两个三角形也不一定全等.

3 结论

上面的举例中,运用适当的反例,我们依次介绍了在只有对应角、对应边、对应周长和对应面积相等的情况下,两个三角形全等的判定情况. 反例除了能说明我们要回答的问题,还能加深学生对数学概念(全等形)的理解. 在举出反例和对反例的分析过程中,学生的问题探究意识得以增强. 相对正规的演绎几何证明来说,在教学中运用反例并不为教师常用,也并非如人们所认为只是举出一个特殊例子那么简单. 这样的理解是比较片面的. 能够举出恰当的反例,它需要先做出猜想和假设,并对假设进行验证,是一个复杂的过程,其重要性不亚于正面的实例讲解[4]. 一个反例并非只是说明一个问题,举得恰当,解释合理,可以是解决一组或一类问题. 教师在举反例的过程中,也需要借助一定的工具(本文中运用了几何画板,也可以用实物教具展示),让学生能体会到从直观认识到演绎推理分析的过程.

不同类型的反例具备不同程度的解释力(explanation power). 在Peled 和Zaslavsky 的研究中[5],提出两个错误的判断四边形全等的命题(若两个长方形的对角线相等,那么它们是全等的;两个平行四边形有一组对边相等,一条对角线对应相等,那么它们是全等的),请在职教师和职前教师举反例说明. 结果发现,在职教师比职前教师更富有经验,举出的例子也更多. 教师们的反例存在不同的水平. 有的教师的例子只能用来说明这个命题是错误的,却无法给出一般性的解释;有的教师能提供一些例子和方法但不够全面;有的教师给出的反例概括出了一般性原理,亦即不单说明命题是错误的,还指出了这一类反例符合的一般性条件. 反例所具备的这种从特殊(只能说明问题是错误的)到一般(还能说明错误的一般原理)的渐变过程,正是波利亚(Polya)在数学问题解决中所提出的,教师需要鼓励学生在特殊和具体的事例中,能够寻找和发现一般的模式和规律[6]. 当然,作为教师,我们不是为了反例而“反”,任何教学内容的组织和设计,都需要根植于具体的问题和情景,基于学生的已有知识和困惑,恰当地在教学中运用反例,有其教学意义,能够促进学生的学习,这也是教师专业知识和能力的体现,在教师的教学和教师教育中需要引起重视.