变易图式在抽象函数性质教学上的应用研究

广东省广州市大同中学(510545) 袁 安

抽象函数的对称性、周期性对学生的抽象能力、推理能力、观察分析能力及解决问题能力有较高的要求,同时也是抽象函数综合应用的基础,是综合解决函数问题的一个重要内容. 本文通过设计变易图式,利用变易图式的四个功能: 对照、区分、类合、融合,强化教学的目的性,更好的引导学生探究发现抽象函数的对称性和周期性.

1 利用变易图式的“对照”功能,初识抽象函数的对称性

对照(contrast),是为了获得对某事物的经验,必须使用其他事物和它形成对比,对照有助于识别关键特征,学生才能直观地意识到事物之间的不同和联系. 所以在研究函数的对称性之前,要与学生原有的对称知识进行对照.

对于数轴上的两实数,x与-x关于实数0 对称,a+x与a-x关于实数a对称,x+a与b-x关于实数对称. 对于函数f(x),若定义域关于原点对称,且对任意x,都有f(-x)=f(x),则我们说函数f(x)是偶函数,且函数图像关于y轴对称,是轴对称图形. 这些都是学生原有的对称知识,为了引导学生进一步去探究出f(a-x)=f(a+x)的性质,设计变易图式1:

变不变审辨关键特征函数关系由f(-x)=f(x)变为f(1-x)=f(1+x)1、自变量x 系数互为相反数不变2、等式左右函数值相等保持不变函数是否仍为轴对称图形? 若是,对称轴是什么?

根据图式要审辨的关键特征,首先引导学生从图形理解,由于1-x与1+x关于实数1 对称,而f(1-x) =f(1+x),显然f(x)关于直线x= 1 对称;其次,引导学生用整体换元的数学思想进行思考,变式后,只是在原来的式子中增加了1个单位,相当于原函数图像向右平移了1 个单位,从而对称轴也平移了1 个单位,由x=0 变为了x=1.

为了进一步探究,给出图式2:

变不变审辨关键特征函数关系由f(1-x)=f(1+x)变为f(a-x)=f(a+x)1、自变量x 系数互为相反数2、等式左右函数值相等保持不变函数是否仍为轴对称图形? 若是,对称轴是什么?

从上面的两种方法,学生很容易就分析得到f(a-x) =f(a+x)的对称轴为x=a. 还可以继续把上面图式的函数关系换为f(x) =f(2a-x),引导学生可以用整体换元的数学思想进行思考,只需令f(a-x)=f(a+x)中的a+x=t,从而有f(t) =f[a-(t-a)] =f(2a-t),由同一函数定义知f(x)=f(2a-x)与f(a-x)=f(a+x)是等价表达式,也相当于是原函数图像向右平移了a个单位,从而对称轴也平移了a个单位.

通过设计变易图式, 从学生已有的知识入手, 让学生更有目的性地进行思考, 引导学生对照得到新的结论, 通过两个图式探究知: 若f(x) 满足f(a-x) =f(a+x) 或f(x)=f(2a-x),函数f(x)的对称轴均为x=a,在这个过程中,要注意把握图式中的不变的关系: 自变量x系数互为相反数,等式左右函数值相等保持不变.

2 利用变易图式的“类合”功能,总结抽象函数的对称轴

“类合”(generalization)指的是如果不同的事物或情况,都出现某种类似或相同的特征(即不变的部分),那么这一特征便会成为所观察事物的一个具有普遍性的维度,会从其他无关的特征中被审辨出来,成为这几类事物的共同特征. 我们在进行抽象的概念教学时要抓住概念的本质特征,可以采用类合这种方式进行教学, 通过找出数学关系的关键特征,使学习内容由多变少,由繁变简,由难变易,达到简化知识形式,提升课堂教学效果.

为了让学生继续深入理解抽象函数的对称轴,设计图式3:

变不变审辨关键特征函数关系变为f(a+x)=f(b-x)1、自变量x 系数互为相反数2、等式左右函数值相等保持不变函数是否仍为轴对称图形? 若是,对称轴是什么?

学生根据以上图式,小组讨论,同学们可以随意改变关系中的a,b的值来进行小组探讨,通过前面的教学,引导学生通过列表代入特殊值观察,再从图像进行归纳总结. 学生根据图式观察猜想得到对称轴教师再引导学生对其进行证明.

证明方法1: 令x=t+得到化简得到所以得到函数f(x)的函数图像关于x=轴对称.

证明方法2: 令x+a=t得到f(t) =f[b-(t-a)]化简得到f(t) =f[(a+b)-t],所以得到函数f(x)的函数图像关于x=轴对称.

由此可知,f(-x) =f(x),f(a - x) =f(a+x),f(x) =f(2a-x) 等都是f(a+x) =f(b-x) 的特殊形式,特点是自变量中的x系数互为相反数,函数值却是相等的,则f(x)的函数图像关于x=轴对称. 图式可以让学生更加明确自己的研究对象和目的,使学生的讨论有明确的方向,提高课堂的效率.

3 利用变易图式的“区分”功能,区分对称轴、对称中心和周期

区分(separation),与“类合”相反,“区分”是指让学生关注变化的方面, 从整体中把握事物的关键属性和关键特征,从而加深学生对事物的深刻认识. 中心对称函数及周期函数都是学生易混,易错的内容,所以在教学中要充分应用图式的区分功能让学生进行区分学习,从而达到真正的理解.

(1)抽象函数的对称中心

若f(x)的定义域关于原点对称,对定义域内的任意一个x,都有f(-x)=f(x),则函数为偶函数,关于x=0 成轴对称,若改为f(-x) =-f(x),函数从偶函数变成了奇函数,图像从有对称轴变成了有对称中心. 函数是轴对称图形时,对称区间相对应函数值相同,函数是中心对称图形时,对称区间相对应函数值相反.

为了区分函数是轴对称还是中心对称,给出下面图式4:

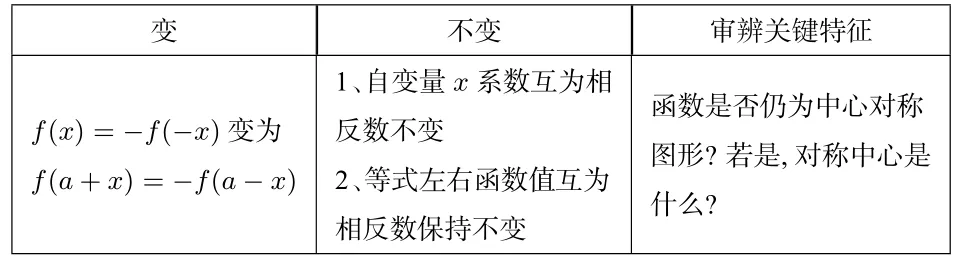
变不变审辨关键特征f(x)=-f(-x)变为f(a+x)=-f(a-x)1、自变量x 系数互为相反数不变2、等式左右函数值互为相反数保持不变函数是否仍为中心对称图形? 若是,对称中心是什么?

学生根据图式4,类比上面的方法,通过列表代入特殊值观察, 让学生从图形理解, 若f(a+x) =-f(a-x),a+x与a-x关于a对称,而函数值互为相反数,则f(x)关于点(a,0)对称,是中心对称图形. 通过区分,虽然函数关系中只多了一个“-”号,函数值互为相反数,但对称性就由轴对称变为了中心对称. 同理,若f(a+x)=-f(b-x),则f(x)关于点对称;若f(a+x)+f(b-x)=c,则f(x)关于点对称. 由轴对称变为中心对称,主要变化就是函数值由原来的相等关系变为了相反关系,其中自变量系数互为相反数是没有改变的.

(2)抽象函数的周期性

为了区分函数的对称性和周期性,给出图式5:

变不变审辨关键特征f(a+x)=f(b-x)关系式变为f(a+x)=f(b+x),即x 的系数由相反变为相等等式左右函数值相等保持不变等距离宽度|a-b|的函数值保持相等,函数有什么性质?

由函数周期的定义知: 若函数f(x) 满足f(x) =f(x+a), 则f(x) 的最小正周期T=|a|. 根据图式, 引导学生思考,函数关系变为f(a+x)=f(b+x),由于x的系数不再是互为相反数,不再具有对称区间相对应函数值相等了,而是等距区间函数值相等,显然函数是具有周期性. 再进一步引导学生根据周期的定义进行换元,找出周期. 把x变为x-b后可变为f(a+x-b)=f(b+x-b)=f(x),根据周期的定义可知f(x)的周期为T=|a-b|. 为了引导学生继续探究函数周期性,根据图式5 继续给出图式6:

变不变审辨关键特征f(a+x)=-f(b+x)函数值由相等变相反自变量的系数相等保持不变等距离宽度|a-b|的函数值互为相反数,函数是否有用周期性?

学生根据图式, 由于x的系数相等, 可知等距离宽度|a-b|的函数值互为相反数,引导学生思考,相反数的相反数就是自身,宽度为2|a-b|的两个函数值就保持相等了. 再次引导学生通过换元找出函数的周期,f(a+x) =-f(b+x),得f(x) =-f(x+b - a), 再次使用-f(x+b - a) =-[-f(x+b - a+b - a)] =f(x+ 2b -2a) =f(x), 所以函数是周期函数,并且周期T= 2|a-b|. 通过图式,让学生区分具有对称性和具有周期性的特点,关键是看x的系数是相反还是相等.

(3)抽象函数的对称轴、对称中心和周期的区分

为了帮助学生区分这三个性质,我们通过下面图式帮助学生理解和记忆,理清知识网.

变不变审辨关键特征函数关系由f(x)=f(-x)变为:f(a+x)=f(a-x),f(a+x)=f(b-x)1、等式左右函数值相等,2、x 的系数互为相反数函数是轴对称图形时,对称区间相对应函数值相同,对称轴为x= 左+右2

函数关系由f(x)=-f(-x)变为:f(a+x)=-f(a-x),f(a+x)=-f(b-x)1、等式左右函数值相反,2、x 的系数互为相反数函数是中心对称图形时,对称区间相对应函数值相同,对称中心为(左+右2 ,0)(其中的“左、右”为等式两边函数关系中的括号内的整体)函数关系由f(x)=f(a+x)变为f(a+x)=f(b+x)1、等式左右函数值相等,2、x 的系数相等函数周期为T =|左-右|函数关系由f(x)=f(a+x)变为f(x)=-f(a+x)f(a+x)=-f(b+x)1、等式左右函数值相反,2、x 的系数相等函数周期为T =2|左-右|

通过图式可以清晰明了地帮助学生区分和理解抽象函数的对称性和周期性,让学生理清知识点,连成知识线,织成知识网,提高学习的效率.

4 利用变易图式的“融合”功能,综合应用并拓展思维

“融合”(fusion)是指“当学习者需要同时理解事物的几个关键特征时,就应该同时体验这几个关键特征的变化”. 通过这个过程,学生能够意识到“变化的这几个方面之间的关系, 以及这些方面与作为整体的学习内容之间的关系”. 解决抽象函数的某些问题时,常常需要根据“对称性”、“周期性”、“奇偶性”中的一个或两个推出另一个. 许多同学望而生畏、一筹莫展,甚至错误地认为三者之间没有必然的联系,为了探究这三者的联系,下面应用变易图式进行学习.

例: 函数f(x)关于x=a对称,同时也关于点(b,0)中心对称,则函数f(x)是否有周期? 若有,周期是多少?

为了更好找出这三者的联系,让学生自己深入探究,引导学生自己设计如下图式,让学生独立思考,相互交流.

图式7:

变不变审辨关键特征有对称中心变为有对称轴原来函数的一条对称轴不变函数图像具两条对称轴,函数是否有周期?

题目变为: 如果函数f(x)有两条对称轴,分别为x=a和x=b,则函数f(x)有周期吗?

图式8:

变不变审辨关键特征有对称轴变为有对称中心原来函数的一个对称中心不变函数具两对称中心,函数是否是有周期?

题目变为: 如果函数f(x)有两对称中心,对称中心分别为(a,0),(b,0),则函数f(x)是否有周期性?

图式9:

变不变审辨关键特征有对称中心变有周期函数原有对称轴不变函数具有一条对称轴和周期,对称轴是否唯一? 有多少条?

题目变为: 如果函数f(x)有一对称轴为x=a和周期T=c(c ＞0),则函数f(x)有哪些性质?

图式10:

变不变审辨关键特征有对称轴变有周期函数原有对称中心不变函数具有一条对称轴和周期,对称中心是否唯一? 有多少个?

题目变为: 如果函数f(x) 对称中心为(a,0) 和周期T=c(c ＞0),则函数f(x)有哪些性质?

利用图式,把抽象函数的对称轴、对称中心和周期三个性质进行组合,有目的地让学生深入探究并进行系统和全面的理解,明确各性质的主要特征和性质之间的相互联系,构建知识网络,对抽象函数的对称性和周期性融合理解,同时又会对照区分,让教学达到事半功倍的效果.

5 教学反思

变易图式的四种功能: 对照、区分、类合、融合,可以帮助学生关注事物“变”或“不变”的部分,审辨事物的关键特征,让学生在复杂的学习环境中理解这几个关键特征之间的关系,以及关键特征与整体之间的关系. 教师通过图式,一步步引导学生对所学知识建立知识网络,形成核心概念图等方式,显示出知识结构和关键特征的变易图式,引导学生对教学过程、呈现过程和思维方式进行反思,提升思维和认知能力,形成自己的学习策略. 将变易图式恰当地运用于高中数学课堂教学,有利于促进学生的有效学习和优化高中数学课堂教学.