从具体到抽象,让思维螺旋上升——一道中考试题的教学设计

江苏省南通市海门区东洲国际学校(226100) 蔡 增

近期,让学生训练了武汉2018年数学中考第24 题,从批阅情况来看,第(3)问的失分较多,主要体现: (1)由于线段CO长含参数m,运算力的要求较高,无从下手; (2)对于符合条件的点有两个无法理解;(3)理解了两个点存在的情况,但只是考虑了当ΔAPD∽ΔBCP时,所得一元二次方程的根的判别式Δ = 0,当Δ＞0,根的存在情况未考虑. 针对以上问题,计划评讲时,考虑给予问题具体数据,逐步呈现能够反映出p的不同个数的不同情况,通过学生比较与归纳发现此类问题的基本规律. 以此为基础,再引入参数,顺势而为,让学生经历拓展与编题,进而完善学生知识发展的厚度.

1 原题呈现

抛物线L:y=-x2+bx+c经过点A(0,1),与它的对称轴直线x=1 交于点B.

(1)直接写出抛物线L的解析式

(2)如图1,过定点的直线y=kx-k+4(k ＜0)与抛物线L交于点M、N. 若ΔBMN的面积等于1,求k的值

(3)如图2,将抛物线L向上平移m(m ＞0)个单位长度得到抛物线L1,抛物线L1与y 轴交于点C,过点C作y轴的垂线交抛物线L1于另一点D.F为抛物线L1的对称轴与x轴的交点,P为线段OC上一点. 若ΔPCD与ΔPOF相似,并且符合条件的点P恰有2 个,求m的值及相应点P的坐标

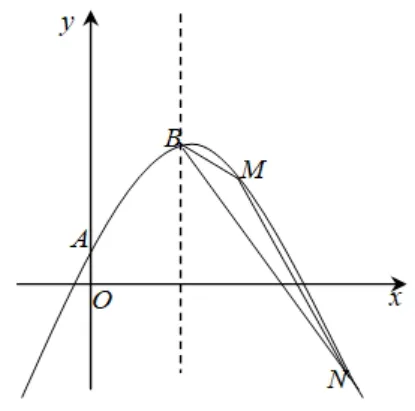
图1

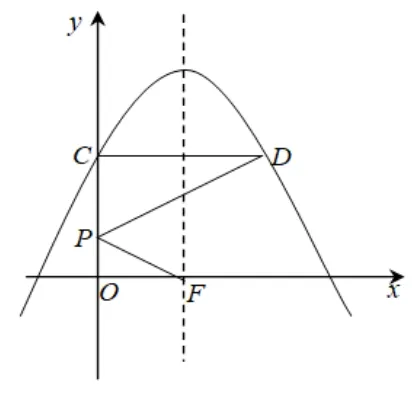
图2

2 教学设计

2.1 题组训练,方法提炼

(1)AD=2,BC=1,AB=4;

(2)AD=2,BC=1,AB=3;

(3)AD=2,BC=1,AB=

(4)AD=2,BC=1,AB=2;

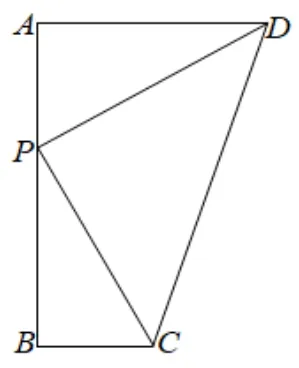
图3

解析: (1)设AP=x,则BP=4-x, 若ΔAPD∽ΔBPC; 则若ΔAPD∽ΔBCP,∴x=2±;∴AP=或

解析: (2) 设AP=x, 则BP= 3- x, 若ΔAPD∽ΔBPC,则;∴x= 2. 若ΔAPD∽ΔBCP,; ∴x1= 1,x2= 2,∴AP=1 或2.

解析: (3)设AP=x,则BP=-x,若ΔAPD∽ΔBPC, 则; ∴x=若ΔAPD∽ΔBCP,; ∴x1=

按：“虋”，涵芬楼、三家本原作“釁”。“虋”字误录。“虋”字罕觏，音mén，义为赤粱粟，乃谷的良种。《尔雅·释草》：“虋，赤苗。”郭璞注：“今之赤粱粟。”明李时珍《本草纲目·谷二·黍》：“赤黍曰虋。”“兇釁”谓祸患、祸乱。《后汉书·隗嚣传论》：“夫功全则誉显，业谢则釁生。”元纪君祥《赵氏孤儿》第三折：“如今削除了这点萌芽，方才是永无后釁。”

解析: (4) 设AP=x, 则BP= 2- x, 若ΔAPD∽ΔBPC, 则若ΔAPD∽ΔBCP,, ∴x无解;

思考: (1)当ΔAPD∽ΔBPC情况下,点P是否必存在? 当ΔAPD∽ΔBCP情况下,点P是否必存在?

(2)在ΔAPD与ΔBPC相似情况下,说说点P个数的变化取决于哪种相似的情况下.

设计说明: 在具体数据背景下, 体验相似的分类及点P个数的变化, 从以上四种情况下, 可以发现当ΔAPD∽ΔBPC时,必存在一个点p,当ΔAPD∽ΔBCP时,点P的存在个数,由所对应的一元二次方程根的情况来决定,尤其对于(2)(3)两种情况,虽然都存在两个不同的点P,但情况是不一样的,一是一元二次方程出现两个等根,二是在一元二次方程出现两个不等根时,出现与前一种情况雷同的位置. 因此当点P的位置有且只有两个时,同样需分两种可能剖析. 在此基础上也可追问学生,当P点位置有且只有一个时,情况有如何?

2.2 参数引入,夯实经验

(5)如图3, 在梯形ABCD中,AD//BC, ∠A= ∠B=90°,AD= 2,BC= 1,AB=m. 点P是AB上一动点,若ΔAPD与ΔBPC相似,符合条件的点p,恰好只有2 个,求m的值.

解析: 设AP=x,则BP=m-x

①若ΔAPD∽ΔBPC,则. ∴必存在一个点P.

②若ΔAPD∽ΔBCP,∴x2-m+2 =0;当Δ=m2-8 = 0 时,则m=(负值已舍)

此时x=与①中x的值不等, 符合题意. 当Δ =m2-8＞0 时, 若满足题意, 则一元二次方程x2-m+2 = 0 的两根中, 必有一根为x=, 代入方程,可求m=3(负值已舍).

综上所述,m=或3.

2.3 类比研究,水到渠成

对于原题中的第(3)问,可以转化为以下问题:

(6) 在梯形ABCD中,AD//BC, ∠A= ∠B= 90°,AD= 2,BC= 1,AB=m+1. 点P是AB上一动点,若ΔAPD与ΔBPC相似,符合条件的点p,恰好只有2 个,求m的值. (过程同上,不再叙述)

2.4 变式拓展,提升思维

(7)如图3, 在梯形ABCD中,AD//BC, ∠A= ∠B=90°,AD= 3BC, 点P是AB上一动点, 若ΔAPD与ΔBPC相似, 符合条件的点p, 恰好只有2 个, 求的值.

设计说明: 把(2)(3)问题中的上下底长由具体数据转化为线段之间的比值,关键考察学生的设参意识及含参一元二次方程的运算能力,进一步提升学生思考问题与解决问题的能力.

2.5 自主编题,动态生成

(8) 如图4, 在矩形ABCD中, 点E,F分别在边AB,BC上,且AE=AB,将矩形沿直线EF折叠,点B恰好落在AD边上的点P处,连接BP交EF于点Q.

①求∠ABP的度数;

③若CD边上有且只有2 个点G, 使ΔGPD与ΔGFC相似,请直接写出的值.

图4

设计说明: 在问题(7)的背景下,以矩形为背景,渗透折叠及面积表示,进而形成梯形中相似存在性问题,让知识得到进一步的综合,形成中档题型,让学生的学会再复杂图形中寻找基本模型.

3 教学感悟

3.1 难点突破需要层层推进

难点问题如何让学生快速内化? 这是每一个教师在教学过程中存在的困惑. 如何把问题知识点靠近学生思维的最近发展区,如何让熟悉知识得到生长,就需要教师精心设计出问题链,让课堂中的每一个学生经历探究、归纳、升华的过程,让每一个学生明白问题的本质,从而达到让每一个学生脑子留痕的效果.

3.2 一题多变,激发学生学习动力

问题的层次性,让不同的学生在学力上得到不同的发展,问题的延续性,易于激发学生探究的热情,在探究过程中,经验积累得到很好的落实. 如本节课中,问题(7)(8)的设置,就能很好地拓展学生思维,让优秀的学生更加优秀. 同时,这样的一题多变体验,更是鼓励学生自主编题,创造性发现问题的最佳时机. 当然,课堂效率的提高、学生自我的成就感、学生学习数学的积极性也就应运而生.

3.3 一题一课的践行

受本节课启发,我们平时的教学过程中,不妨选择一道有价值的题目或材料与学生一起研究,一起挖掘其中的学习线索,一起发现问题的本质. 对于学生来讲,何尝不是一次头脑风暴. 反道而行之,我们也可让问题开放设计,一起体会数学知识的生成与组合,一起欣赏同学应答的精彩,真正让我们的数学课堂充满数学味.