历史视角下的数学活动探究课设计*——“数形结合”进行开平方运算

广东实验中学(510375) 罗 瑾

1 背景

《义务教育数学课程标准(2011 版)》指出:“课程内容要反映社会的需要、数学的特点,要符合学生的认知规律. 它不仅包括数学的结果,也包括数学结果的形成过程和蕴涵的数学思想方法”[1]. 在数学的教学中,教师不仅要注重知识的传授,使学生掌握相关的结论,更应注重数学的发现与形成.有的教师只讲知识,不讲其来龙去脉以及应用;教材中通常注重知识的逻辑结构, 忽视了知识的形成过程和文化背景,数学教学“把火热的发明变成了冷冰冰的美丽”. 作为一线教师,应该将这种“冰冷的美丽恢复为火热的思考”,通过合作探究、数学建模、借鉴数学史等,让学生体验知识的形成过程,享受发现数学的乐趣. 数学史是数学家们发现与创造数学的过程,其中蕴含了丰富的数学思想,体现了数学家们的智慧,教师可以通过数学史与课堂相结合的形式开展数学活动.

数学史融入数学教学的研究是数学教学研究的重要组成部分,是HPM(数学史与数学教育国际研究组)领域的重要方向之一[2]. 数学史在数学教学中的运用通常有3 种方式,一是提供直接的历史信息,二是借鉴历史进行教学,三是开发对数学及其社会文化背景的深刻觉悟. 其中第二种方式就是依据历史发生原理的发生教学法,其实质是指个体数学理解的发展遵循数学思想的历史发展顺序,即“历史相似性”[3].美国数学史家卡约黎(F.Cajori,1859～1920)指出,通过数学史的介绍,教师可以让学生明白: 数学并不是一门枯燥呆板的学科,而是一门不断进步的生动有趣的学科[4]. 既然如此,我们应该将数学史引入课堂,让学生了解知识的产生,甚至处于数学家们最初发现、创造数学的状态,亲身体验做数学,对数学进行再创造的过程.基于上述原理及方法,本文以数学史的视角设计了一节数学活动课.

1.1 问题情境

在人教版八年级上册15.2 节中出现了图1,此图除了教材中提到可作为完全平方公式的几何解释之外,还有何妙用之处?

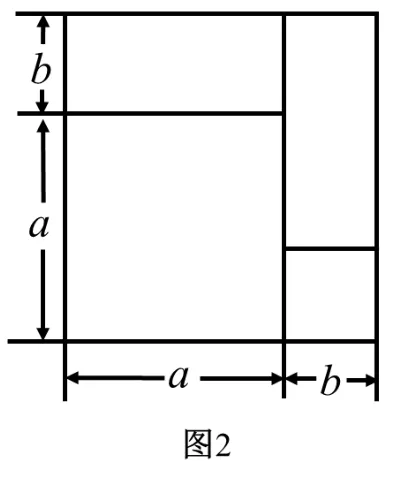
在数学史上,图1 曾经被数学家们用来解决许多与“平方”有关的问题,例如解方程的正根、求一正实数的算术平方根等. 教师可以收集相关资料,借鉴数学史进行教学,提高学生学习数学的兴趣,让学生对数学进行“再创造”,理解数学的本质,培养学生积极探索的科学精神.

1.2 数学史视角

早在公元前3 世纪,古希腊数学家欧几里得在《几何原本》卷2 有如下命题:“任意分一线段成两段,则整段上的正方形等于两分段上的正方形与两分段所构成矩形的二倍之和”. 如图2 所示,若以a、b表示两分段长,则上述命题就是

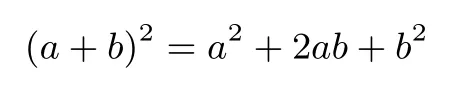
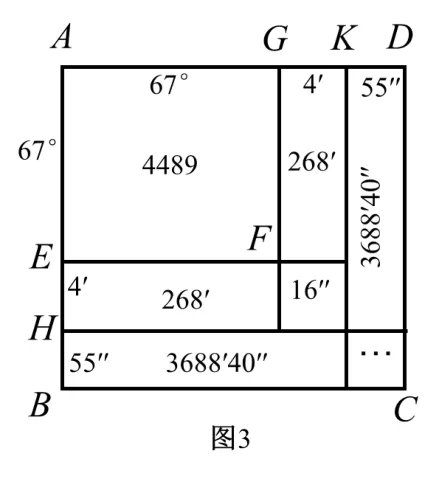
既然图1 与两数的平方有关系,那么它能否解决一个基本的问题——任意一个数开平方呢? 如图3 所示,在亚历山大时期(公元前356年至323年)的数学家西翁给出了关于托勒密结果的几何图示(希腊人采用的是60 进制)[5].

开平方的问题得到初步的解决,那么一元二次方程是否可以利用上述图形来解出正整数解呢? 9 世纪阿拉伯数学家花拉子米(Al-Khwarizmi, 约780～850)解二次方程时附加了几何证明. 在《代数学》第4 章,花拉子米给出了二次方程

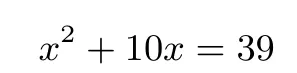
除此之外, 在斐波纳契的《算盘书》中, 图1 被用来求得了如图6, 构造边长为的正方形[5].

在这个简单图形的背后竟然有着如此美妙的应用! 如果能将这丰富的数学知识展现在学生眼前,势必引起他们的好奇心与兴趣. 对此,笔者提出两种处理方式: 一是在学生学到相应的内容时将其融入到课堂中;二是将上述内容单独作为一堂数学活动课,同时给学生提供探究性学习的课题. 此内容在教材中的连贯性不强,如果教师认为在正常的课堂教学上不好处理,那么可以考虑将其作为校本课程等其他非正常教学进度的兴趣课堂上. 下面笔者根据此内容设计一节数学活动探究课.

2 基于数学史的设计

目前我国采用螺旋式上升的教材体系,学生对数学知识的认知逐渐深入,但在学生的数学认知结构中,很难形成完整的知识网络结构体系,知识变得零碎,不系统. 实际上,许多数学知识是相通、联系的. 本节课能让学生经历数学再创造的过程;体会数学知识是关联、相通的;还能体会代数几何法的美妙之处,图形与代数的完美结合. 另外,也可启发学生可以继续探究“图体一说”的数学问题.

2.1 几何图形的引入

问题1 利用几何图形解释完全平方公式.

学生利用在15.2 节中已有的经验,给出图1、图2.

教师向学生介绍此图在《几何原本》的历史,并引导学生将数与形结合起来.“平方”在“形”中可以表现为正方形的面积,让学生体会数形结合的思想,强调可以利用“形”对“数”进行解释.

2.2 合作讨论,展示交流成果

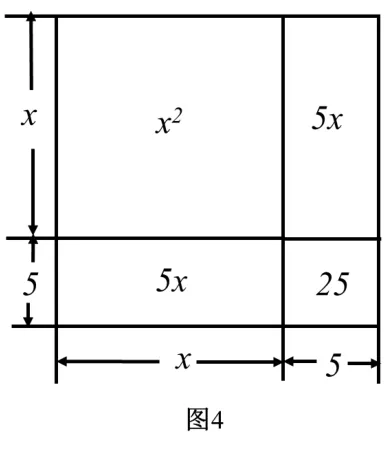
问题2 如何借助图形解一元二次方程x2+10x=39?

学生分组讨论,每组选一名代表汇报,展示所在组的讨论结果.

结果1 从出发: 构造以x2为边长的正方形,以及两个长为x、宽为x的矩形(图4). 可知边长为x+5 的正方形面积为64,即边长为8,x为3.

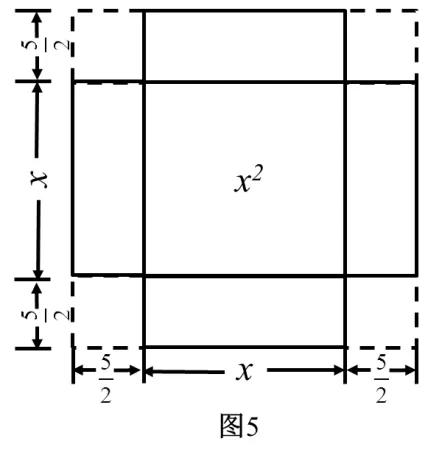
结果2 从x2出发: 构造以x为边长的正方形,以及四个长为x,宽为的矩形(图5). 可知边长为的正方形面积为64,即边长为8,x为3.

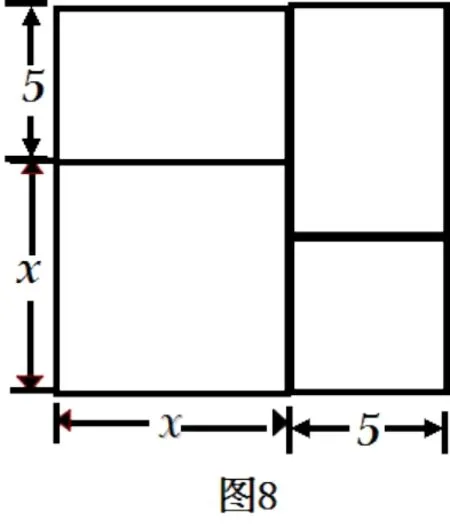
结果3 先进行配方得(x+5)2= 64,从(x+5)2出发:构造以x+5 为边长的正方形(图7、图8). 可知边长为x+5的正方形面积为64,即边长为8,x为3.

问题3 借助图形,求7569 的算术平方根.

学生自行思考,并画出图形;分组讨论,交流结果.

学生展示: 将原问题转化为求一个面积为7569 正方形的边长. 先进行估算,以80 为边长的正方形面积为6400,剩下的面积为1169. 通过计算发现当长方形的宽为7 时恰好符合(图9).

问题4 借助图形,求8436 的算术平方根近似值(保留整数).

学生利用问题3 相似的方法进行思考,但8436 并非完全平方数,引起学生认知冲突,让学生尝试去解决真正的问题. 先自行思考,再进行小组讨论、交流看法.

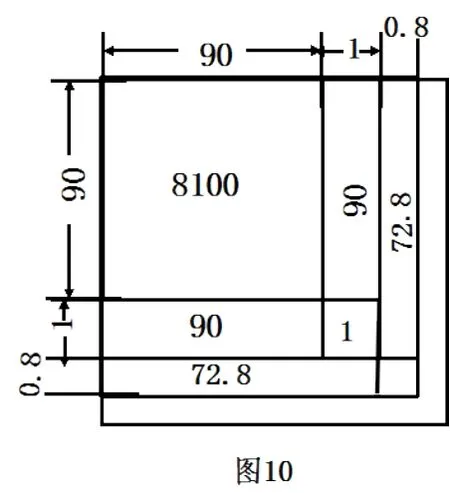
学生展示: 将原问题转化为求一个面积为8436 正方形的边长. 先进行估算,以90 为边长的正方形面积为8100,剩下的面积为336. 通过计算发现当长方形的宽为1 时,两个长方形(长为90)与小正方形的面积最接近336,剩下的面积为155. 计算发现当长方形(长为91)宽为0.8 时,两个小长方形与小正方形的面积为146.24,较接近155,始终无法恰好相等(图10). 因此,8436 的算术平方根取整数后为92.

对于平方根,学生在人教版八年级上册第13.1 节中只学习了用得比较多的较小数的平方根,但对于一般的数,直到高中都没有提及到如何开平方. 这是一个十分基本的问题,却一直到高中教材都没有提及到. 对此,学生必定会产生疑问. 笔者认为,如果将此内容放在学完本文需要的知识基础后,教师利用数学史中数学家西翁的方法,同时给出开平方的除法竖式,并进行讲解,对于学生来说是能接受并且是能理解的.

2.3 总结升华,提出研究问题

教师进行总结并引导学生提出更多问题,作为课后探究.

(1)其他与“平方”有关的问题,如(a+b+c)2、(a+b+c+d)2等的几何证明;

(2)将此图证明与“平方”有关的问题推到立方, 如(a+b)3、(a+b+c)3等的几何证明;

(3)对于存在正根的方程ax2+bx+c= 0(a,b,c ∈R),怎样构造图形?

(4)对于(a+b)2有没有其他的几何证法?

(5)寻找更多图形与代数完美结合的问题等.

上述问题可作为学生研究性学习的课题. 学生完成的方式可以多种多样,可以写一份本节课后的感想,也可以对自己感兴趣的问题,查找资料,形成读书报告或写成一篇小论文等.

本文从数学史的角度,借鉴有关利用图形进行开平方运算的历史进行教学,设计了以上的数学活动探究课,让学生经历做数学、再创造的过程. 这只是数学史这片汪洋大海中的冰山一角,仍有许多可作为课堂教学的丰富素材有待挖掘.教学中融入数学史,既能使学生在掌握知识的同时了解知识的形成过程,加深对数学知识的理解,又能让学生了解到数学是经历演进过程的学科,而不是天上掉下来的东西. 因此,教师应该多了解数学史,积累素材,适当地在课堂教学中融入数学史,渗透数学文化,提高学生学习数学的兴趣.