造境·串问·灵动:从中考题谈情境教学*
——以“直尺作图”为演示案例
江苏省镇江市宜城中学(212028) 张 洁
1 问题的提出
省视当下,尺规作图复习题与中考题都会考查经典的尺规作图问题,结合复习课,目前面临着以下问题: 尺规作图基本概念掌握不牢固、数学复习课堂单向传输、尺规作图到直尺作图创新转化困难. 这些问题使尺规作图复习课堂效率不高,有必要在教学方式上进行创新,下文拟从“情境”与“问题串”的视角作一些探讨.
2 情境教学课堂演示案例
2.1 示例1
(2019年浙江· 嘉兴卷· 改编) 在6×6 的方格纸中, 点A、B、C都在格点上,按要求画图:
问题1: 在图1 中找一个格点D,使以点A、B、C、D为顶点的四边形是平行四边形.
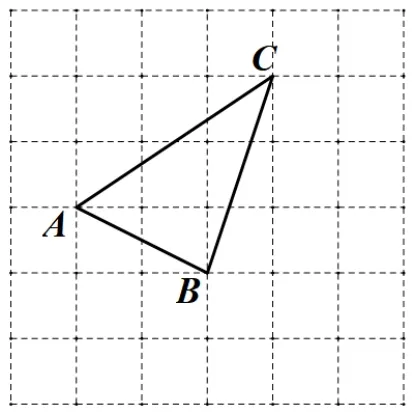
图1

图2
师: 我们学习过尺规作图和网格作图,你能找到对应的点吗,你是如何找到呢?
生: 如图2,根据平行四边形的性质,对边平行且相等,数格子可以找到对应的D1,D2,D3.
问题2: 在图3 中仅用无刻度的直尺,把线段AB三等分(保留画图痕迹,不写画法).
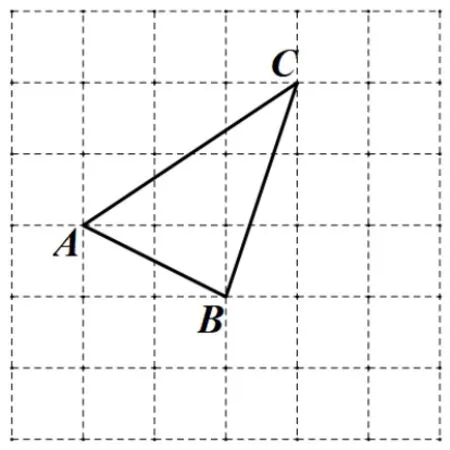
图3
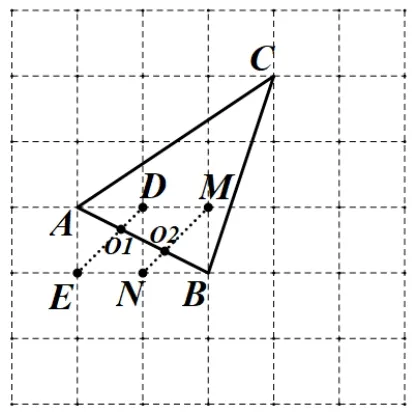
图4
师: 根据我们复习的尺规作图、直尺作图的内容,你会画什么平分线呢?
生: 垂直平分线.
师: 虽然没有复习过三等分点的画法,你能借助直尺与网格以及图形的性质找出三等分点吗?
生: 可以,如图4,我们可以找到格点D、E、M、N,连接DE、MN,与AB交于O1,O2,所以AO1:AO2= 1 : 2,同理得出O1,O2是三等分点.
问题3: (改编题) 在图5 中仅用无刻度的直尺, 画出∠APD的角平分线(保留画图痕迹,不写画法).

图5
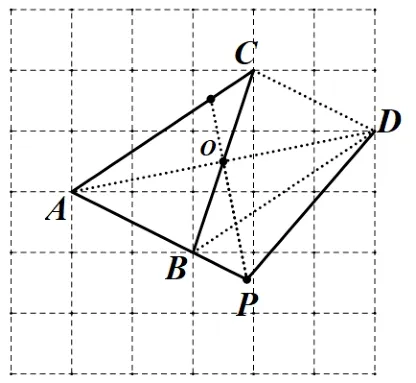
图6
师: 三等分点我们运用了相似三角形的知识,而图5 出现了非格点,你会利用什么工具解决呢?
生: 直尺和圆规.
师: 但是问题3 给出的限定条件是: 仅用无刻度的直尺.你有解决办法吗?
生: 我们探讨发现,D是问题1 中的D2点,我们可以利用问题1 中的平行四边形的性质,连接CD、AD、BD,AD与BC交于O,再根据等腰三角形的性质,连接PO并延长,即PO为角平分线.
评析: 在苏科版八年级上册课本中,提到垂直平分线的尺规作图. 本题三等分点难度较大,借助九年级已学相似三角形的有关知识,从垂直平分线引出三等分点的问题串. 由问题改编加入问题3,因为在直尺作图的情境问题串的条件下,无法用圆规作图,只能利用直尺,所以本题又回到八年级等腰三角形的基本性质的知识点上,问题迎刃而解. 问题3的加入,可以让学生充分利用问题1 与2 的结论思考并解决问题,从“造境”到“串问”,环环相扣,让学生变得灵动.
2.2 示例2
(2019年天津卷· 改编) 边长为1 的正方形网格中, ΔABC的定点A是格点,B是中点, ∠ABC= 50°,∠BAC=30°,经过A、B两点的圆,圆心在AC上.
问题1:AB=____;
师: 如图7,如何利用网格计算线段长度?
生: 根据勾股定理知:AB=
问题2: (改编题)用无刻度的直尺,找出圆心O;
师: 在复习过示例1 的前提下,你会利用直尺作图吗? 你能说出理由吗?
生: 如图8,找到格点E、F,连接EF,与AC的交点即为圆心O.
问题3: 请你在给定的网格中, 用无刻度的直尺, 在ΔABC的内部画P,使其满足∠PAC= ∠PBC= ∠PCB,并简要说明P的位置是如何找到的(不要求证明)_______.

图7
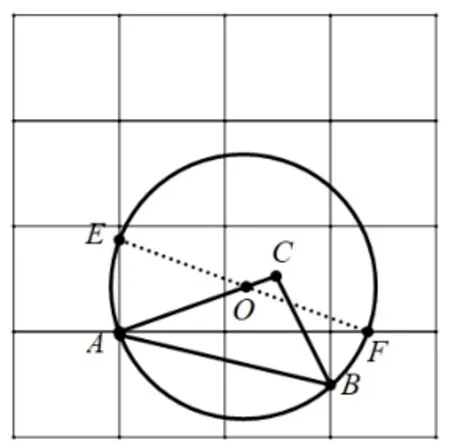
图8

图9
师: 画角相等你会用什么方法呢?
生: 尺规作图画一个角等于已知角.
师: 问题3 的限定条件仍然是直尺作图,你是用什么基本知识解决的呢?
生: 如图9, 设AB与格子交于D点, 连接DO并延长交于Q, 因为D是AB的中点, 所以OD⊥AB,易 知ΔQOC∽= ΔBOC, 所 以QC=BC, ∠QCO=∠OCB= 100°, 所以得∠PCB= ∠PBC= 20°, 由此得ΔAOP∽= ΔQOP,即∠PAC=∠PCB=∠PBC=20°.
评析: 本题难点在于问题,大部分学生不明所以. 本题根据圆的有关性质,改编加入问题2,造境、串问并让学生感到题目不再陌生. 结合三角形全等的性质得出推导过程,重现本题的重难点,让学生读透问题串,掌握问题三角形全等与圆有关性质的本质,让课堂变得如此灵动.
2.3 基础知识的回归——追根溯源
仔细阅读上述3 道中考题及改编题,可以看出,题目中的情境问题串已经指向课本中的三角形、平行四边形、圆的相关知识点,但学生在复习过程中很难看透问题中的知识点.此时,需要教师引导学生复习书本知识,系统整理课本关联知识,找到其知识本源,回归课本知识,以不变应万变.
3 尺规作图情境教学探讨
3.1 引导——从单一到系统
由已学知识转化为对未知问题的解决,需要对知识的整理、消化. 中考复习课,教师可以根据中考真题加入情境以及问题串, 作好知识铺垫, 引导学生不断探讨, 提高学习兴趣.以上文中“直尺作图”为例, 由2 道中考题引申到n个知识点,举一反三. 九年级学生学习习惯已经养成,可以在教师的引导下, 改变过去单纯由教师讲解知识点的传统教学模式,通过题串让学生动起来,把自主权交给学生.
3.2 设问——从单向到互动
九年级学生在掌握了3年的数学知识的基础上,复习时间较长,难度较大,部分学生对数学感到厌倦. 新题型的情境问题串引入,可以提高学生的学习兴趣和学习能力,也使教学不再枯燥无趣. 上文的中考题都是以情境问题串为核心内容,以“直尺作图”作为切入点,以情境问题作为探讨的线索,循序渐进地贯彻到中考题的每一个问题中. 改编题型以课本的知识为情境,围绕三角形、平行四边形、圆的有关性质进行情境层层设问,自然过渡到已经复习的知识点. 为此,教师在复习过程中,需要肯定学生的创造性,引导其透过表象看本质,提高复习效率,促进核心素养提升.
3.3 引申——从旧知到新知
从2019年尺规作图的题型可以看出,“直尺作图”并不是书本上提到的内容,学生遇到新题型感到束手无策,其主要原因在于对书本知识掌握不够牢固. 嘉兴题则是从平行四边形入手,问题串“直尺作图”的切入点则是相似三角形的基本性质、等腰三角形的三线合一基本性质;天津题则是从圆的相关知识作为切入点,问题串的解决是结合三角形全等的基本判定定理. 这些知识是我们中考复习中书本的基础知识,也是复习重点. 直尺作图虽然是新题型,但是教师复习时加入题串可以让学生自然地过渡到新知.
4 结语
中考复习中,教师要根据新课标的要求,引导学生从中考题看基础知识,也就是说,要促使学生在原有的数学活动经验基础上,思考数学知识的发生、发展过程. 中考复习时间紧、任务重,要在有限的时间内提高复习效率,就要系统地复习书本基础知识,回归课本. 教师在中考复习中根据真题设置情境问题串,引导学生牢固掌握旧知,并结合情境的引导,让学生不断从旧知引申出新知,理解、掌握新知,有效提高考试成绩.

