六何引导数学教学 先行组织培养思维*
——以“对数函数及其性质”教学设计为例
广西师范大学数学与统计学院(541006) 林素安 刘存华 周 莹
1 问题提出
《普通高中数学课程标准(2017年版)》明确指出“在数学课堂中要培养学生的逻辑推理能力,将学生思维能力的培养贯彻于整个教学过程中”[1]. 可见高中数学是关注“过程”的教学,注重学生思维能力的培养,传统课堂提问的问题层次太低,过于注重知识的记忆,缺少思维性[2]. 许多一线教师在教授新授课时往往会忽略学生的最近发展区,在课堂中的提问超出了学生的能力范围,体现不出学生思考的过程,导致学生学习新授课时思路不清晰,难以理解新知的本质. 因此,如何在新授课中使学生明晰知识的本质,由浅入深的培养学生的思维能力是一个亟待解决的问题. 本文尝试在新授课中以“六何”认知链指导先行组织者的应用,构建以先行组织者为载体,培养学生思维能力为主线的课堂教学模式,并给出教学设计过程,以期为帮助学生明晰新知的本质、培养思维能力提供新的方法路径.
2 “六何”认知链与先行组织者的整合
2.1 “六何”认知链理论
“六何”认知链是周莹教授基于如何在新授课中培养学生思维提出的一种教学过程理论.“六何”认知链以问题情境出发,从问题意识的角度进行教学设计,展现了知识的来龙去脉,具有问题性、可操作性、层序性以及完整性,具体内容如下[3]:
“从何”: 新知从哪里而来;“是何”: 新知的本质属性和特征是什么;“与何”: 新知与旧知有何区别及联系;“如何”: 所学新知如何学以致用;“变何”: 对新知或问题的条件、结论、方法进行螺旋上升的变式;“有何”: 总结归纳本节课在知识、情感、方法上有何收获[3].
2.2 先行组织者理论
先行组织者由美国的奥苏贝尔于上个世纪60年代提出.“先行组织者”指先于数学知识前,呈现给学习者的一种引导性材料,可帮助学习者建立新旧知识间的联系,进而加强新知识的学习[4].“先行”二字指知识建构过程的先行,引导材料可在学习过程中的任意阶段呈现. 因此,先行组织者的功能是为新知识提供观念上的固着点,通过对学习者原有的知识结构进行加强,从而达到促进学习者的有意义学习和记忆保持的目的. 根据学习者对新知识学习的熟悉程度,先行组织者可分为陈述型组织者和比较型组织者;根据组织者和新的学习内容之间的包容层次和抽象程度可分为上位组织者、下位组织者和并列组织者[5].
2.3 “六何”认知链与先行组织者整合的教学模式
“六何”认知链做为一种理论指导需要应用于具体的教学实践中,而先行组织者作为一种应用型材料则需要系统的理论指导. 将先行组织者进行分类后的“陈述型组织者、比较型组织者、下位组织者、并列组织者”与“六何”认知链有着互通点,都注重知识的来龙去脉、构建认知过程的手脚架. 因此,将“六何”认知链与先行组织者进行有机的整合,并凝结于教学设计当中,可帮助学生搭建认知的手脚架,做好知识间的过渡,明晰新知的本质,逐步培养学生的思维能力[6]. 将分类后的先行组织者与“六何”认知链整合成教学模型(如图1),并依此进行新授课的教学设计.

图1 教学模型
3 先行组织者在“六何认知”指导下的教学设计
先行组织者是为开启学生思维提供的教学材料,在课堂上得到很好的实施需要一定的理论指导. 本文在中国知网近几年与“对数函数”相关文献的研究基础上,尝试运用上述教学模型整合、优化“对数函数及其性质”一节内容,并将教学过程设计如下:
3.1 课例背景
“对数函数及其性质”选自《高中数学人教A 版》(必修一)2.2.2 节,继指数函数的图形与性质的学习之后,是对函数图像的深入认识,也是研究基本初等函数图像及性质的基础,在本章中具有衔接的作用. 本节课的主要内容是通过对比指数函数性质的探究学习方式,进而探究得出对数函数的图像及性质,并将其运用于解决实际问题中. 学生在本节课的学习之前已具有一定的探究函数图像能力. 以“六何”认知链指导先行组织者在各教学环节中的运用,培养学生的思维能力.
3.2 教学过程
(1)追溯从何,引入新知
基于“对数函数从哪里来? ”的思考,通过引入生活中的例子创设问题情境,提出“先行组织者”,在观察具体函数例子的过程中,得出对数函数的定义.
问题1考古学家一般通过提取附着在出土文物、古遗址上死亡生物体的残留物,利用估算出土文物或古遗址的年代. 根据问题的实际意义可知,对于每一个碳14 含量p,通过对应关系都有唯一确定的年代t与它对应,那么t和p有什么函数关系?
问题2大西洋鲑鱼每年都要逆流而上, 游回产地产卵. 研究鲑鱼的科学家发现鲑鱼的游速可以表示为函数单位是m/s,其中o表示鱼的耗氧的单位数,那么v和o有什么函数关系?
设计意图巴金说:“方向比努力更重要”. 故以“从何”为教学的起点,对“对数函数从何而来”进行思考,创设生活中的“问题情境”这个先行组织者,使学生找准本节课的学习目标,激发学生浓厚的学习热情,从观察具体函数中完成对对数函数的首次感知,形成对数函数模型,为探究对数函数的性质做铺垫.
(2)探究是何,把握本质
基于“对数函数的性质有哪些? ”的思考,在学生探究的过程中引出“陈述组织者”,把握对数函数性质的本质.
问题3在数学中如何定义上述问题中形如y= logax的函数? 其值域和定义域的取值范围是什么?
问题4为什么在对数函数解析式y= logax中,a >0,且a ̸=0,x >0?
问题5如何利用函数的性质研究y= log2x和的图像? 绘制并观察这两个函数图像, 可以得到哪些结论?
设计意图“是何”目的是明晰知识点,把握所学知识的本质属性. 从学生的最近发展区出发,使用问题导向法提出问题3、4,使学生明晰对数函数的本质属性,理解每个字母及取值范围的含义. 再基于学生已有的探究能力,引导学生绘制出两个最基本的对数函数图像. 在学生对比观察的过程中引出“陈述组织者”,把握对数函数图像的本质内容,完成对对数函数的二次感知,从中渗透数形结合的数学思想,培养学生的思维能力.
(3)关联与何,拓展概念
基于“对数函数的性质与哪些知识有关? ”的思考,引导学生对比探究“比较组织者”,设计如下问题:
问题6回忆上节课所学习的内容,有哪些知识点与对数函数有联系?
问题7用类似探究指数函数的方法,小组内进行合作探究,选取底数a的若干个不同的值,观察不同底数的对数函数在同一直角坐标系内的图像,你们有什么发现?
问题8能不能把你们的发现整理成表格?
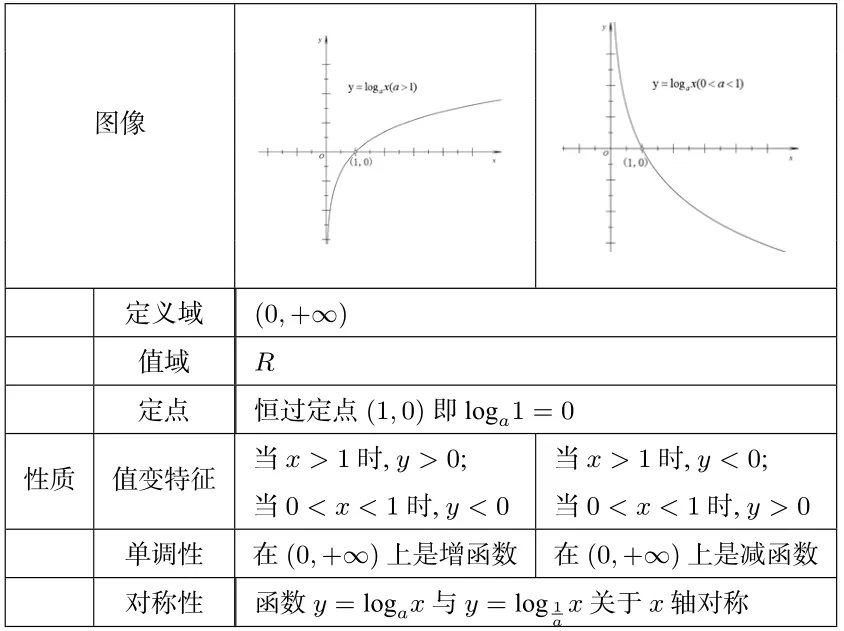
表2:对数函数的性质
设计意图“与何”目的在于联系相关知识,完善知识体系. 教师再次充分利用学生的最近发展区,在学生的能力范围内引导学生进行小组合作,探究“比较组织者”. 通过比较底数在0<a <1、a >1 范围内不同对数函数的图像,将抽象的对数函数直观化,体会不同底数对对数函数性质的影响,从而培养学生的直观感知能力及数形结合思想,完成对对数函数的第三次感知,拓展对数函数的概念. 在问题8 整理归纳中,使学生形成系统的知识框架(如表2),为“如何”打下坚实的知识基础.
(4)操作如何,学以致用
学生探究出对数函数的性质后,掌握的效果如何? 对学生进行当堂检测:
问题9求下列函数的定义域
(1)y=logax2;(2)y=loga(4-x)
问题10比较下列各组中两个值的大小
(1)y=log23.4,y=log28.5
(2)y=log0.31.8,y=log0.32.7
(3)y=loga5.1,y=loga5.9(a >0,且a ̸=1)
(4)如图3 所示,有四个对数函数
①y=logax, ②y=logbx, ③y=logcx, ④y=logdx
试比较a,b,c,d的大小

图3
设计意图“如何”是本节课的关键点. 教师通过强化“并列组织者”,对学生提出了两道简单的求定义域问题和比较大小问题. 目的在于考查学生是否掌握了对数函数的定义域为x >0,以及如何应用图像比较对数值的大小. 在学生的实际操作过程中,体会如何应用对数函数的性质解决简单的问题,再次深化学生数形结合的思想,培养学生的思维,加深对对数函数的理解,完成对对数函数的第四次感知.
(5)拓展变何,深化概念
基于“拓展对数函数的性质”,引导学生拓展“下位组织者”,设计如下问题:
问题11在指数函数y= logax中,x为自变量,y为因变量. 如果把y当成自变量,x当成因变量,那么x是y的函数吗?
问题12运用对指互化公式,绘制y= log2x与y= 2x的图像,你们有什么新的发现?
问题13通过观察可以发现这两个函数关于y=x对称,如何给这样的函数下定义? 还可以绘制出其他类似的函数吗?
设计意图“变何”是本节课的高潮部分.“变式拓展”可以帮助学生多角度地理解知识本质,生长出对对数函数性质新的认识. 教师通过拓展“下位组织者”,学生可发现对数函数的新性质: 与同底的指数函数互为反函数. 通过问题13 让学生自己给函数下定义,体验数学的严谨性,深化对数函数的性质,发散数学思维,完成对对数函数的第五次感知.
(6)反思有何,构建体系
基于“学习本节课后有什么收获”,师生共同进行小结:
问题14今天的课堂即将接近尾声,让我们共同梳理本节课学习的流程有哪些?
问题15有哪位同学可以将今天的收获用思维导图呈现出来吗? (师生共同完成)
设计意图“有何”在一堂课中起到了画龙点睛的作用.先通过梳理本节课的学习思路,加深学生对所学内容的印象.再通过充分运用先行组织者策略关联相关知识,师生用思维导图共同绘制本节课的框架体系(如图4),将所学知识纳入已有认知体系,形成“组织者”整体,完善学生的知识结构,培养学生的系统思维[7].
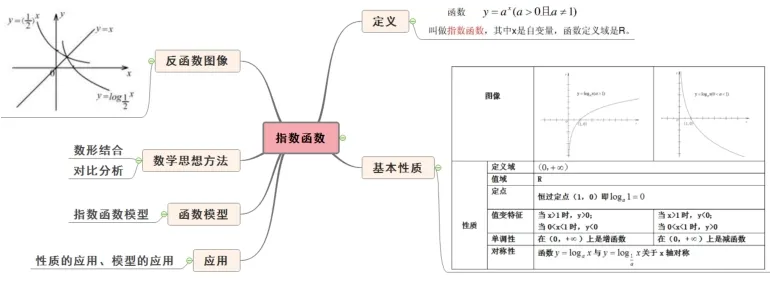
图4 指数函数思维导图
4 教学反思
4.1 在教学目标的设计上,选择组织者
一堂好课离不开教师精心的设计. 要在一堂课中由浅入深的培养学生的思维,教师在教学目标的确定时就要充分考虑学生的最近发展区,利用学生已有的知识经验来设计教学过程. 在哪个教学过程中应用哪个组织者来引导学生进行学习? 怎样通过组织者来培养学生的思维? 都要在教学设计中有所体现,体现出先行组织者的可操作性. 将“六何”认知链与先行组织者进行整合,形成教学模型,使得每个教学过程都有理论指导,帮助教师梳理教学思路,选择合适的组织者进行教学.
4.2 在六何认知的指导中,应用组织者
依据学生的最近发展区,开展教学活动,应用先行组织者: 在“从何”中提出“先行组织者”;在“是何”中引出“陈述组织者”;在“与何”中探究“比较组织者”;在“如何”中强化“并列组织者”;在“变何”中拓展“下位组织者”;在“有何”中形成“组织者”整体. 以指数函数的教学为例,在课堂导入环节以具体的例子呈现“先行组织者”,降低学生的理解难度,并在接下来的学习中依次应用不同的组织者,发挥各自不同的优势,逐步培养学生的思维.
4.3 在教学问题的设计下,培养思维力
在“六何”认知指导下的问题设计由浅入深,逐步带领学生由潜意识的思维进入到深层次的思维,调动学生学习的积极性,并给予学生学习的成就感. 如在“与何”环节的合作探究,由三个由浅入深的引导性问题,引领学生进入数学探究的世界,在探究中发现成就并培养思维. 学生思维的培养不仅体现在一节课中,还需要在整个教学中不断的渗透. 教师对学生思维的培养任重而道远,需要教师不断地进行教学反思,尝试将该教学模型应用于其他类型课程,尝试新的教学方法,探究出一条发展学生系统思维的道路.

