能力立意,素养导航*——赏析2019年北京大学优秀中学生暑期课堂试题

北京市怀柔区京市第一O 一中学怀柔分校(101407) 李加军

2019年北京大学优秀中学生暑期课堂测试早已落下帷幕. 这份试题源于课本又高于课本,试题整体区分度较大,前三题入手较易,却令人耳目一新,后两题需要学生具备适当的拓展知识,如高次方程韦达定理、第二数学归纳法及抽屉原则等内容.

数学课程目标首先要求学生在学习数学的过程中掌握数学基础知识、基本技能、基本思想、基本活动经验(简称“四基”);其次,在应用数学的过程中提高从数学角度发现和提出问题的能力、分析和解决问题的能力(简称“四能”);进而在学习数学和应用数学这两个过程中发展数学抽象、逻辑推理、数学建模、直观想象、数学运算、数据分析等数学学科核心素养;最后,能够会用数学眼光观察世界,会用数学思维思考世界,会用数学语言表达世界(简称“三会”). 数学学科核心素养是课程目标的集中体现,“三会”是数学学科核心素养的外在表现.

这套试题很好地落实了数学课程目标,考查了学生的数学学科核心素养. 下面笔者对试题进行赏析,以飨读者.

1. 已知函数f(x)满足f(f(x))=x-1,问: 是否存在整数n,使得f(n)是整数. 若存在,求出所有的n;若不存在,请说明理由.

分析存在性问题的一般思路是假设存在,然后按照题目条件进行合理推导,最后如果推出矛盾,则得出结论不存在;如果推出结果,则需要进一步对结果进行检验来确定结论是否存在.

解假设存在n,m ∈Z, 使得f(n) =m, 则f(m) =f(f(n)) =n -1, 进而f(n-1) =f(f(m)) =m -1,f(m-1) =f(f(n-1)) =n-2,依此类推有f(n-k) =m-k,且f(m-k)=n-(k+1)(k ∈N).

(1)若n=m,则f(n)=n且f(n)=n-1,矛盾!

(2) 若n ＞ m, 由m=n -(n - m), 知f(m) =f[n-(n-m)]=m-(n-m)=2m-n,又f(m)=n-1,故2m-n=n-1,即2n=2m+1,矛盾!

(2) 若m ＞ n, 由n=m -(m - n), 知f(n) =f[m -(m - n)] =n -(m - n+ 1) = 2n - m -1, 又f(n)=m,故2n-m-1=m,即2n=2m+1,矛盾!

综上可知,不存在整数n,使得f(n)是整数.

说明本例通过假设存在n,m ∈Z,使得f(n) =m,易得知f(n-k)=m-k,且f(m-k)=n-(k+1)(k ∈N),进而分类讨论得出矛盾,从而获得结论是不存在. 解题过程体现了逻辑推理、数据分析等数学核心素养.

2.已知函数f:{1,2,3,··· ,2019} → {-1,1}, 若i,j ∈{1,2,3,··· ,2019}, 证明:不成立.

分析是否成立问题一般适应于反证法. 由于函数f:{1,2,3,··· ,2019} →{-1,1}, 从而问题的本质是1-2019 的函数值可否两两乘积之和为0, 其必要条件是乘积f(i)f(j)的个数为偶数.

证明反证法: 假设由f(i),f(j)∈ {-1,1}, 则f(i)f(j)∈ {-1,1}, 于 是中f(i)f(j) 取值-1 和1的个数一样多, 所以一定有偶数个乘积f(i)f(j). 而事实上中f(i)f(j) 的个数是== 2019×1009(奇 数) , 矛 盾! 所 以

说明通过反证法, 分析出题目本质就是判断中应该有偶数个乘积f(i)f(j), 而事实上个数为奇数,水到渠成,得到问题结果. 解题过程体现了逻辑推理、数学计算等数学核心素养,细思之下,脑海际会浮现一种曲径通幽之快乐.

3. 已知等腰直角ΔABC,∠A= 90°,点D在边AB上,点E在边AC上,满足AD=AE,过点A,D分别作BE的垂线交BC于点P,Q,用平面几何方法证明:PC=PQ.

分析此题证明线段PC=PQ, 但PC,PQ没有直接联系,因此需要将其中一条转移到一个新的图形中,再找到该图形与另一条线段所在图形的关系(如全等),从而使得问题加以解决.

证明延长EA至点F, 使得FA=EA, 连结FB交BC的平行线AG于点G, 连结GD. 因为AG//BC, 所以∠GAD=ABC= ∠ACB= ∠GAF,又AD=AE=AF,GA=GA,所以GAD∽=GAF,故∠ADG=∠AFG.

由∠BAC= 90°, 以 及AP⊥BE,DQ⊥BE, 知∠ADG= ∠AFG= ∠AFB= ∠AEB= ∠BAP=∠BDQ, 所以∠ADG= ∠BDQ, 所以G,D,Q三点共线,所以GAPQ是平行四边形,所以GA=PQ.

再 由∠BAC= 90°, 以 及AP⊥BE,DQ⊥BE, 知∠ABG= ∠ABF= ∠ABE= ∠PAC, 故在ΔABG中与ΔCAP中, ∠ABG= ∠PAC, ∠GAB= ∠PCA= 45°,AB=AC, 所以GAB∽= ∠PCA, 所以GA=PC, 于是PC=PQ.

说明由上述分析, 考虑平移PQ到AG, 此时根据结论可以倒推出ΔABG与ΔCAP全等, 但由于还不知PC=PQ, 反过来却不易证明此全等关系. 于是转变思路,作对称变换,得到与ΔABE全等的ΔABF,进而得到与ΔCAP全等的ΔABG,并证明GAPQ是平行四边形,从而由传递关系得出PC=PQ. 解题过程体现了直观想象、逻辑推理等数学核心素养.

4. 实数满足x+y+z=x2+y2+z2=2,求xyz的最大值和最小值.

分析首先由条件可以解得xy+yz+zx= 1,结合结论可以联想到三次方程的韦达定理处理,进而构造三次函数讨论其有三个零点的条件解决问题. 其次也可以由条件消去z,然后分析消元后x,y的二元结构式可知将t=x+y整体化处理,利用基本不等式找到t的范围,并讲结论化为t的三次函数,利用导数法求其最值.

解方法一: 由题意得xy+yz+zx= 1, 所以x,y,z是关于t的方程t3-2t2+t - r= 0 的三个实数根, 其中r=xyz, 设f(t) =t3-2t2+t - r, 则f′(t) = 3t2-4t+ 1 = 0 的根为t=或t= 1, 结合图象可知

方法二: 由x+y+z= 2, 得z= 2- x - y, 代入x2+y2+z2=2 整理得x2+y2-2x-2y+xy+1=0. 设t=x+y,由x2+y2-2x-2y+xy+1=0 得xy=t2-2t+1,又z= 2-x-y= 2-t, 因此xyz= (t-1)2(2-t), 由t2-2t+ 1 =xy≤解得等号在x=y时取到. 令g(t) = (t-1)2(2- t), 则g′(t) = (t -1)(5-3t) = 0 的根 为t= 1 或t=从而易知g(t) 在上单调递增, 在上单调递减, 又g(1) =g(2) = 0,所以当g(1) =g(2) = 0 时(如取x=y= 1,z= 0),r=xyz取最小值0,当时(如取r=xyz取最大值

说明方法一逆用三次方程韦达定理,构造出相应的三次函数,结合三次函数存在三个零点的条件找到xyz的范围,进而确定等号取到条件,求出xyz的最值,使得问题迎刃而解. 方法二充分利用消元的思想和整体化的思想将表示为的函数,并用基本不等式确定出的取值范围,把问题转化为函数在给定区间上的最值问题,利用导数判断单调这一工具如鱼得水. 解题过程中体现了逻辑推理、数学抽象、数学运算等数学核心素养.

5. 有10 条长为1 的线段,每一条都被分为若干条小线段. 证明: 总可以选取6 条小线段,使它们可以构成2 个三角形.

分析如果一条线段所分出的所有小线段内部构不成三角形,则可以推出最长那个小线段长度不低于接下来通过分类并对每条线段所分出来的最长小线段结合抽屉原则得出本题结论.

证明假设某一条线段拆出的小线段们不能构成三角形, 不妨设这些小线段的长度从小到大依次是a1,a2,··· ,an, 则ai+1≥ai+ai-1对每个i= 2,··· ,n-1(n≥3)都成立(否则存在ai-1,ai,ai+1三个就能构成三角形了) . 下面用数学归纳法来证明: 对任意2 ≤m≤n,m,n ∈Z,有

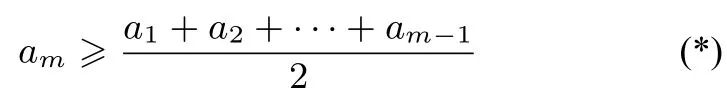
当m= 2 时,显然有a2≥a1＞,所以不等式(*)成立;

当m= 3 时,显然有a3≥a2+a1＞,所以不等式(*)成立;

假设当m≤k(k≥3)时成立,则当m=k+1 时,根据归纳假设2ak-1≥a1+a2+···+ak-2,所以2ak+1≥2(ak+ak-1)≥ak+ak-1+2ak-1≥a1+a2+···+ak-2+ak-1+ak,即ak+1≥,所以m=k+1 时,不等式(*)也成立.

由数学归纳法知对任意2 ≤m≤n,m,n ∈Z, 有

进而可知: 对于“一条拆出的所有小线段不能构成三角形”的线段, 有an≥(n≥2), 即所以(n≥2), 当n= 1 时, 显然有从而说明若某一条线段拆成的所有小线段不能构成三角形,则拆出来的最长小线段

现在来考虑所有的10 条线段,分成三类情况:

(1)已经有2 条线段,它们拆出来的小线段可以各自构成三角形了,则问题得证.

(2)若只有1 条线段拆出来的小线段能自己构成三角形,考虑另外9 条线段, 每条线段都有1 条长度不小于的小线段,于是这些小线段的长度要么位于中,要么位于中,由抽屉原理,9 条线段放入两个区间里,至少有一个区间里有3 条线段. 又因为显然落在这两个区间任意一个里的三条线段是能组成一个三角形,于是问题得证.

(3)若没有1 条线段拆出来的小线段能自己构成三角形,考虑10 条线段,同情况(2)可知选出3 条构成三角形;再考虑余下的7 条线段,同情况(2)能再选3 条构成三角形,从而问题得证.

说明数学的应用性使得数学焕发出无穷的魅力. 这个例子说明有意识地培养灵活的数学观念,深刻认识题目中所蕴含的数学本质,积极利用数学工具解决实际问题,对提高一个人的数学素养乃至综合素养有着极大的帮助. 解题过程体现了数学抽象、数学建模、逻辑推理等数学核心素养.