“基于素养,能力立意”引领下的思维培养——运动轨迹为圆的问题常见类型

浙江省宁波市镇海区仁爱中学(315200) 邓 俊

《普通高中数学课程标准》修订组提出了六大数学核心素养,即数学抽象、数学推理、数学建模、直观想象、数学运算和数据分析. 作为核心素养之一的数学抽象,鲍建生教授曾在《高中数学课程标准修订中若干问题》一文中指出,其有以下四个方面的表现: 形成数学概念和规则、形成数学命题与模型、形成数学方法与思想、形成数学结构与体系. 由此可见形成数学模型是数学学习过程中重要的抽象,它的教学是培养学生抽象能力的重要环节. 如何让学生利用模型解决涉及动点的几何最值问题,这类问题综合性强、难度大,能全面考察学生对平面几何问题的解决能力,各省市中考时常将其作为压轴题. 解决这类问题最常用的一种方法是: 首先寻找动点的运动路径,在一类运动路径为圆的问题中难点往往在于如何发现圆,而有了圆以后问题也可以变得更为丰富. 既可以是线段的最值问题,也可以是角度,面积等常见几何量的问题. 下面就初中阶段常见的圆轨迹做归纳整理.

1 定点定长——圆轨迹

例1 如图1, 等腰直角ΔABC中, ∠ABC= 90°,AB=CB=2,CD=求∠BAD的范围.

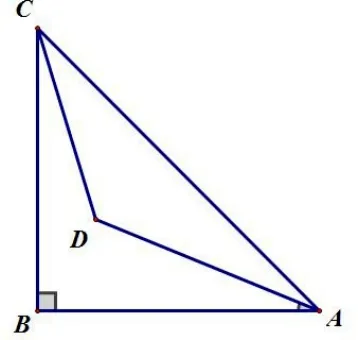
图1

图2

分析: 因为CD=所以点D在以C为圆心,为半径的圆上(如图2). 当直线AD与⊙C相切时,∠BAD取到最值. 又因为2CD=CA所以当∠ADC= 90°时,∠CAD=30°,所以15°≤∠BAD≤75°.

小结: 到定点的距离等于定长的点的轨迹为圆,而题目中的呈现方式往往会给出定点和定长,隐去它的轨迹. 解答时将其轨迹画出,可以使得解题变得更加直观. 当有了圆轨迹之后,问题也可以变得更加丰富,可以求线段AD的最值,也可以求ΔACD面积的最大值等等问题.

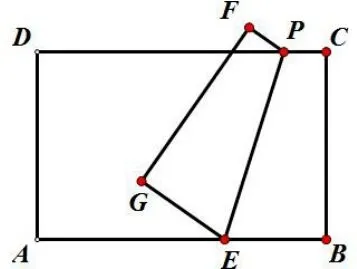
例2在矩形ABCD中,AD= 6,AB= 6+,E是AB边上的一点,且AE=AD,P是线段CD上一点,连接PE,将矩形沿着PE折叠,点B、C分别落在G、F处,当点P从点C移动到点D时,点G经过的路径长为_______.

例2 图

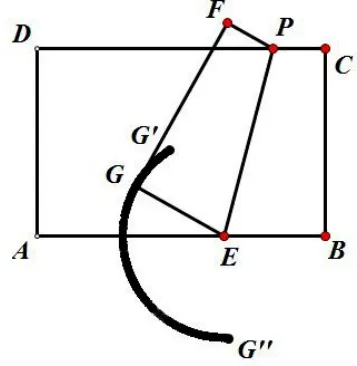
图3

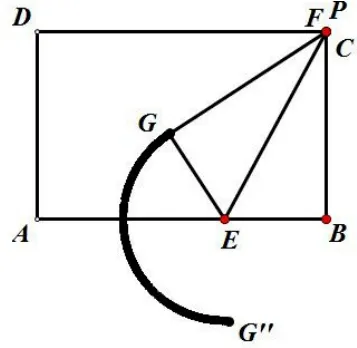
图4

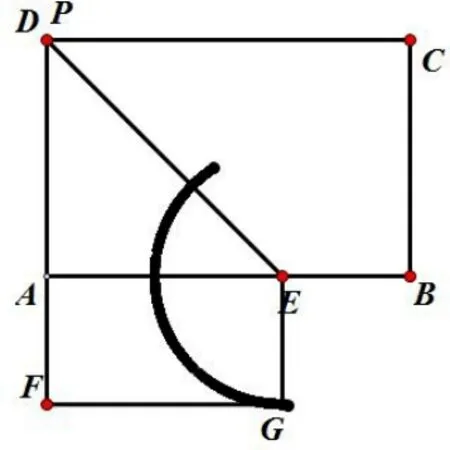
图5

分析: (如图3)因为折叠的过程中GE=BE=所以点G在以E为圆心,为半径的圆弧上. 点P在线段CD上从C移动到点D的过程中,当点P在C点时(如图4) 点G在G′的位置, 由题意得:EB=,CB= 6,∠B= 90°得出∠CEB= 60°, 则∠GEA= 60°. 点P在点D时(如图5) , ∠PEB= 120°, 则∠AEG= 90°, 所以整个弧的圆心角是150°, 那么点G经过的路径长为:

小结: 本题是到定点的距离等于定长的点的轨迹为圆弧而不是圆,主要是要找出圆弧的起点和终点然后求出圆心角,这样圆弧的路径长就迎刃而解.

2 定弦张角——圆轨迹

例3如图6, 在平面直角坐标系中,O为原点, 点A(-2,0), 点B(0,2), 点E, 点F分别为OA,OB的中点.若正方形OEDF绕点O顺时针旋转,得正方形OE′D′F′,记旋转角为α. 若直线AE′与直线BF′相交于点P,求点P的纵坐标的最大值.

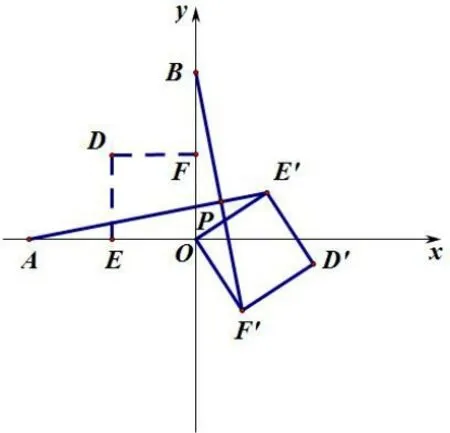
图6

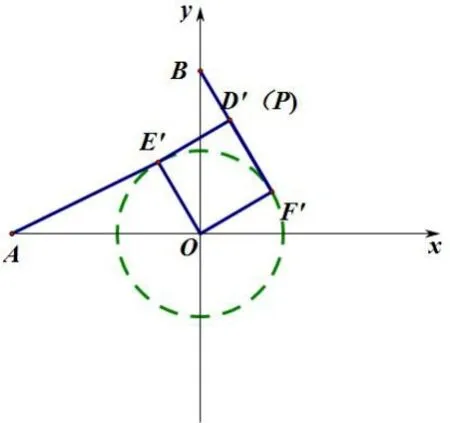
图7

分析: 如图6, 当正方形旋转时, ΔBOF′可以由ΔAOE′绕点O顺时针旋转90°得到, 所以BF′⊥AE′, 即∠APB= 90°恒成立,AB=是定值, 所以点P在以AB为直径的圆上运动. 要求点P纵坐标的最大值, 即求∠E′AO的最大值, 因为E′的以O为圆心, 1 为半径的圆上,当AE′与⊙O相切时,∠E′AO最大为30°,此时点P与点D′重合(如图7),所以AP=点P的纵坐标为

小结: 此题可以看成相似等腰直角三角形(ΔAOB、ΔEOF)的绕直角顶点旋转问题,那么点P为对应点连线的交点,此时点P是两三角形(ΔAOB、ΔE′OF′)外接圆的交点. 此题也可以看成两个全等三角形(ΔAOE′、ΔBOF′)旋转90°的问题,那么点P为对应边所在直线的交点,显然对应边也互相垂直,所以对于线段AB的张角∠APB= 90°,点P在以AB为直径的圆上. 此题点P运动轨迹圆弧所对的圆周角∠PAO有一定的范围,所以点P的圆弧有一定的度数范围. ∠PAO最大为30°,所以此时点P的纵坐标最大.

例4如图8,ΔABC、ΔEFG均是边长为2 的等边三角形,点D是边BC、EF的中点,直线AG、FC相交于点M.当ΔEFG绕点D旋转时,求线段BM长的最小值.

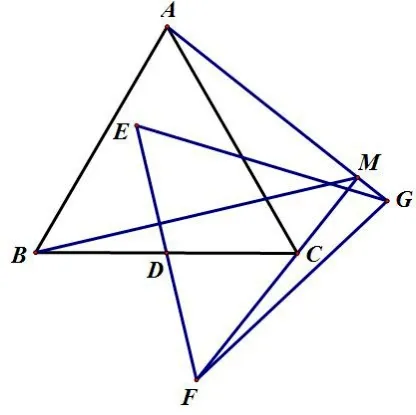
图8

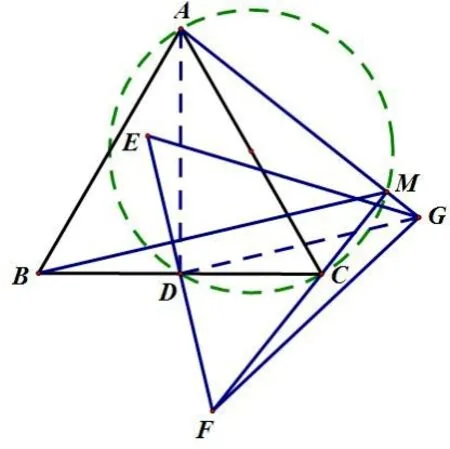
图9

分析: 如图9, 连结DA,DG, 在正ΔEFG旋转的过程中, ΔDFC可以由ΔDGA绕点D顺时针旋转90°, 并缩小倍得到,所以CF⊥AG,即∠AMC= 90°恒成立,AC= 2 是定值,所以点M在以AC为直径的圆上,那么问题就转化为圆外点到圆上点距离的最值问题了, 易得BM的最小值为

小结: 此题可以看成两全等直角三角形(ΔADC、ΔGDF) 绕直角顶点旋转问题, 点M为对应点连线的交点,点M是两个三角形(ΔADC、ΔGDF)外接圆的交点. 此题也可以看成两相似等腰三角形(ΔADG、ΔCDF)绕顶点旋转90°的问题,那么点M为对应边所在直线的交点,显然对应边也互相垂直,所以对于线段AC的张角∠AMC固定为90°,那么点M的轨迹为以AC为直径的圆.

3 定圆变换——圆轨迹

例5在平面直角坐标系内, 点A,B,C的坐标分别为(4,0),(0,4),(-2,0),以C为圆心,CO为半径画圆,点P在⊙C上运动. 如图13,将AP绕点A顺时针旋转90°至AE,求线段BE的范围. 如图15,将线段AP绕点P逆时针旋转90°至PF,求ΔABF面积的最大值.

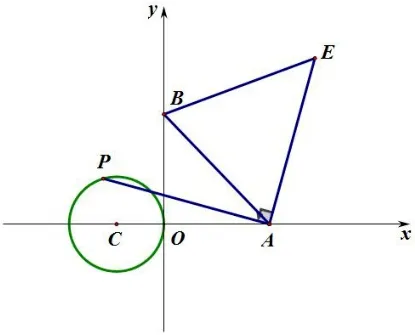
图10

图11

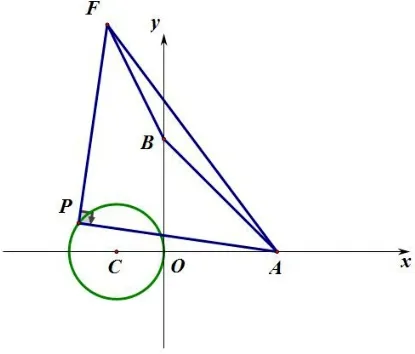
图12

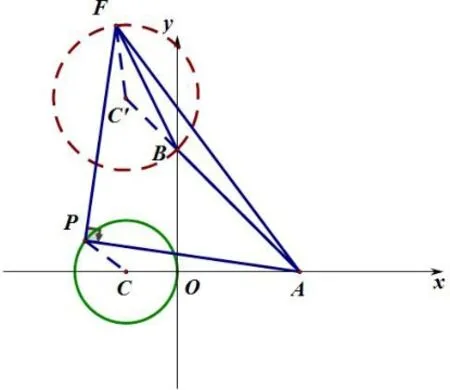
图13

分析: (1)将AP绕点A顺时针旋转90°至AE,所以点E的轨迹由点P的轨迹旋转而来,点P的轨迹是圆,那么点E的轨迹也是圆. 点E的轨迹圆圆心也由点P的轨迹圆心绕点A顺时针旋转90°而来,C(-2,0)绕点A顺时针旋转90°至点C′(4,6),此时连结EC′,PC,因为∠PAC= ∠EAC′,AC=AC′,AP=AE, 所以ΔPAC∽= ΔEAC′, 可得EC′=PC= 2, 所以点E的轨迹为以C′(4,6) 为圆心,2 为半径的圆(如图11),问题就转化为圆外点到圆上点的距离最值问题,所以将AP绕点P逆时针旋转90°至PF,那么AF也可以看成AP绕点A顺时针旋转45°并扩大倍得到. 那么点F的轨迹由点P的轨迹旋转并扩大倍得到,点F的轨迹圆心也由点P的轨迹圆心变换而来,AC绕点A顺时针旋转45°并扩大倍得到AC′,点C′为(-2,6). 此时连结FC′,PC,因为∠PAC= ∠FAC′,所以ΔPAC∽ΔFAC′, 可得FC′=所以点F的轨迹为以C′(-2,6)为圆心,为半径的圆(如图13),那么当FC′⊥AC′时,ΔABF的面积最大为8.

小结: 此类问题通常由圆绕定点旋转,放缩产生新的圆,从而形成一些关于圆的常规问题,隐蔽性较强. 解题者若对于变换后的图形轨迹没有清晰的认识,那么解题会变得异常困难. 解决此类题目的关键在于理解点与轨迹的关系,从对应点变换到轨迹圆变换,再到轨迹圆心变换都是相同的变换,可以利用这样的观点,先找到圆心,再证明变换后的点轨迹是圆. 证明的过程往往是全等,相似等三角形知识的综合运用,再结合圆的定义得到圆轨迹.

例6如图14,在等腰RtΔABC中,AC=BC=点P在以斜边AB为直径的半圆上,M为PC的中点. 当点P沿半圆从点A运动至点B时,求点M运动的路径长.

分析: 点M为CP线段的中点,线段CM可以看成线段CP缩小到原来的一半. 那么点M的轨迹就是点P的轨迹缩小原来的一半. 所以点M的轨迹圆心由点P的轨迹圆心变换而来. 取AB中点E,点E为点P轨迹圆圆心.取CE的中点F,因为M为PC中点,F为CE中点,所以2MF=PE= 2 恒成立. 即点M到定点F的距离始终等于1,所以点M的轨迹为半圆(如图15),路径长为π.

图14

图15

小结: 此类问题可以归结为圆上动点到定点的连线上一个固定比例点的轨迹问题,也可以看成圆的位似变换,解决此类问题的关键就是找到变换后轨迹圆心的位置. 通常情况下,可以连结圆心与定点,在此连线上,再结合固定比例找到圆心位置. 确定好圆心的位置后,在通过三角形知识证明变换后点的轨迹是个圆,问题就迎刃而解了.

本文通过对动点问题中的轨迹为圆的这些常见题型进行剖析,我们深刻感受到轨迹为圆的魅力. 找到隐藏的圆化无形为有形,看透点运动内在联系,培养学生的核心素养.