经历估测 建立猜想 转化验证 提升素养——关于“圆的面积”的教材对比与教学尝试

翟运胜（特级教师）

一、“圆的面积”教材版本对比

圆是学生在小学阶段学的最后一个平面图形，也是在小学阶段唯一要学习的曲线图形。圆在第一、二学段的数学教学中占据着重要地位，具有较高的教育价值。由于圆是曲线图形，探索它的面积公式比直线图形要稍难一些。在探索圆的面积公式的过程中可以使学生进一步体会“转化”的思想方法，渗透极限思想，增强空间观念，发展数学思维，提升核心素养。各种版本的数学教材在编排“圆的面积推导”这部分内容时，都力图充分体现这一知识点的教育教学价值，让学生在经历中成长。纵观人教版、苏教版、北师大版、浙教版小学数学教材中关于“圆的面积”的编排，大致可以分成两类：一类是直奔主题，直截了当，如北师大版、人教版；另一类是估计猜测，推导公式，如苏教版、浙教版。

1.编排类型一：直奔主题，直截了当。

北师大版（图1）在编排“圆的面积”时，直接提问：如何得到一个圆的面积呢？学生以往的经验是数格子，但是由于圆是一个曲线图形，会出现不满整格的现象，这种方法仅能求出一个圆的大约面积，不能迅速准确地求出圆的面积，显然是不方便使用的。基于已有的数学活动经验，学生顺理成章地想到能否把圆转化成以前学过的图形，在这个过程中，强化了学生转化的意识，提升了迁移类推的能力。这样的编排相对直接，教师课堂教学实施相对比较容易，对学生可能想到的探究路径进行充分地预设与应对，符合学生的认知规律，容易引发学生的探究兴趣。

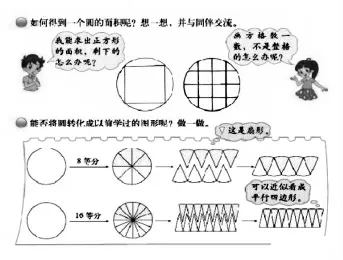
图1

人教版教材在编排“圆的面积”教学时，与北师大版教材类似，创设了这样一个问题情境：每平方米草皮8 元，这个圆形草坪的占地面积是多少平方米？引导学生提问：怎样计算一个圆的面积，引发学生探求圆面积的内在需要。在教学中，教师引导学生想一想能否把圆转化成以前学过的图形，从而推导出圆面积的计算公式。这样的编排在常态化的实施过程中，有的教师会直接演示把圆沿着直径切开，拼摆成近似的长方形推导出公式，教学过程中学生有可能会成为“操作工”。教学中，教师应当给学生尝试、遇阻、折回，找最佳切割方式的机会，组织引导学生经历思维曲折的探索过程。

2.编排类型二：估计猜测，推导公式。

苏教版教材在编排“圆的面积”（图2）教学时，设置了两个例题，例7 是引导学生体会圆的面积与半径的平方之间的关系。在此之前，学生没有探究圆面积计算的需求，需要教师另外设计课堂教学，考虑到常态课的教学状况，如果能把创设面积计算的情境隐含在其中，对一线教师能有所暗示就更好了。在例7 中，以正方形的边长为半径画出大小不同的圆，让学生借助正方形来估计圆的面积，通过数格子计算圆的面积大约是正方形的几倍，也就是半径的平方的几倍。从而发现圆的面积与半径的平方之间的关系。例8 则是把圆等分成若干份，然后拼成长方形来推导出圆的面积公式。在这个过程中发展学生有序思考和简单推理的能力。在实际教学时，这两个例题放在一节课中，在家常课的状态下，一节课的教学时间是挺紧张的。从例7 的教学来看，教师引导组织的痕迹比较重，学生多是在教师的指令与点拨下操作与思考。因为一般情况下，学生很难想到以正方形的边长为半径画出大小不同的圆，以此探索圆的面积除以它的半径的平方是否存在规律。人类对于圆面积的研究经历了千百年的时间，想在一节课中帮助学生经历这一过程，自然需要教师精心地预设、点拨和讲授。没有教师点拨引导，学生很难想到借助正方形来尝试求圆的面积，体会圆的面积可能是这样的正方形面积的几倍，也就是半径的平方的几倍，然后再通过例8 的公式推导进行验证。

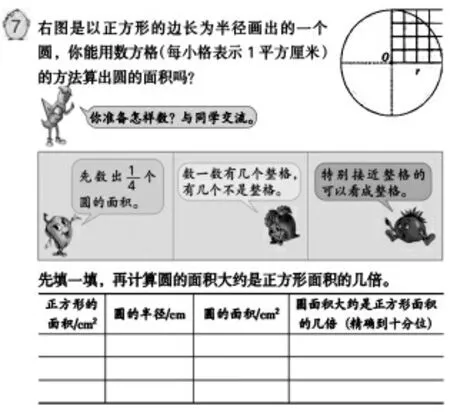
图2

浙教版教材在编排“圆的面积”（图3）这部分内容时，同样也采用了类似估计与猜测的编排，引导学生思辨：圆的面积与小正方形的面积（圆的半径的平方）有什么关系，利用图形中的不同颜色来帮助学生思考。由于有颜色区分的暗示，多数学生能够理解圆的面积大于它半径的平方的2 倍，小于半径的平方的4 倍。不过浙教版没有安排数格子来具体计算圆的面积与小正方形面积之间的倍数关系。教学实践证明，学生在数格子计算圆的面积时，很难把格子数清楚。在计算公式推导的过程中，不仅组织学生把等分后剪开的圆形拼成长方形，还引导学生把等分后剪开的圆形拼成梯形、三角形或者是把圆形等分成32 份后不剪开，把其中的一份看作是一个小三角形，从而推导出圆的面积计算公式。这个编排以数学知识内在的魅力吸引学生，提升学生的数学核心素养，引发学生的数学研究兴趣。此处对学生的操作要求与思维能力，以及教师的课堂驾驭能力提出了较高的要求，学力水平较低的班级不适合采用这种教学方式。

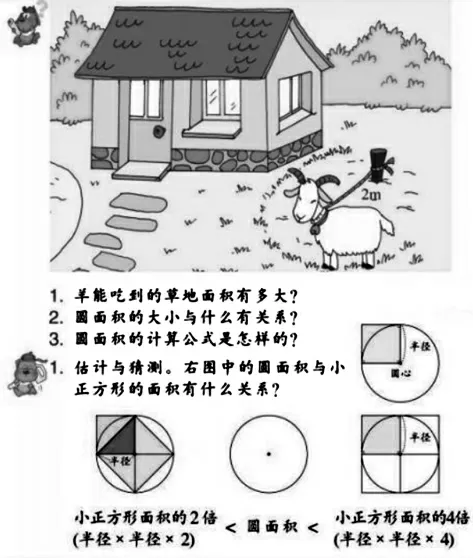
图3

二、思考：估计猜测的环节是否必要呢？

北师大版与人教版在编排中直截了当引导学生把圆的面积转化成已学图形，从而推导出圆面积的计算，此内容较利于家常课的教学开展，而估测环节似乎不是必需的。苏教版与浙教版在编排圆的周长计算时，借助一个圆的外切正方形和一个内接的正六边形，确定了圆的周长与直径之间关系的范围，从而使猜测有据可依，并通过这一过程培养学生的推理能力。遵循这一设计思路，在编排圆的面积探索学习时，也加入了这样一个估计猜测的环节，从提升学生数学核心素养的角度来看显然是必要的，并且渗透了探究方法的习得。不同地域学生的学习背景差异较大，无论采用哪一种编排，在实施教学中都应当结合学生实际情况而定，不可概而论之。不过，即便加入这个猜测过程，也应当重新设计，让学生在真实经历曲折探索的过程中提升数学核心素养。

三、教学尝试

1.创设情境，引起探究欲望。

师：（出示一个自动旋转喷水器动画）它旋转一周所喷灌的地方是一个什么样的图形呢？

生：圆形。

师：关于圆我们已经知道些什么？

（学生依次说出圆心、半径、直径、周长等相关的知识点）

师：根据这个情境，你会提出什么样的问题呢？

生：自动旋转喷水器旋转一周所喷灌的土地面积是多少？

2.建立猜想，引发验证需要。

师：这其实就是求圆的面积，通过对圆的周长的探索学习，我们得出了这样一个结论：圆的周长是它直径的π 倍，也就是三倍多一些。对于圆的面积，你会有怎样的猜想呢？

生：圆的面积是不是与直径之间有固定不变的倍数呢？

生：圆的面积与半径之间是不是有固定不变的倍数呢？

师：（出示半径为3cm、4cm、5cm 的圆）我们怎样知道这些圆的面积，有什么方法吗？

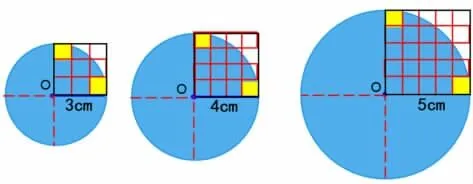
图4

生：我们可以采用数方格的办法来求出圆的面积。

师：为了方便数方格与计算，我们借助了与圆有一定关系的正方形，先数出四分之一圆的面积，再计算出整个圆的面积。

师：由于圆是曲线图形，像图中对角线两端的两个方格，非常接近满格的算作满格，其余不满一格的按半格计算。

（学生填一填，然后依次汇报，完成下表）

?

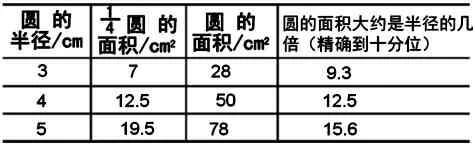
师：你有什么发现呢？

生：我们发现用圆的面积除以半径以后，商并不是一个固定不变的数。

师：用圆的面积去除以相应圆的直径呢？

（学生用计算器计算发现，圆的面积与直径之间也没有固定的倍数关系）

师：看来圆的面积与半径和直径都没有明确的倍数关系，那么它与什么有关系呢？请看下图。

（课件依次出示）

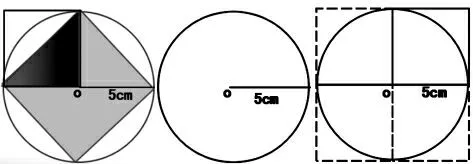
图5

师：从这幅图中，你能得出圆的面积与小正方形之间有怎样的关系呢？先独立思考，再小组讨论。

生：圆的面积一定小于正方形面积的4 倍。

生：圆的面积一定大于正方形面积的2 倍。

师：圆的面积大于正方形面积的2 倍，而小于正方形面积的4 倍。

师：小正方形的边长是圆的半径，这句话还可以怎样说呢？

生：圆的面积大于它半径的平方的2 倍，而小于它半径平方的4 倍。

师：根据这幅图，你又会提出怎样的猜想呢？

生：圆的面积会不会与半径的平方之间有固定不变的倍数关系呢？

（教师出示下面的表格，学生填写）

?

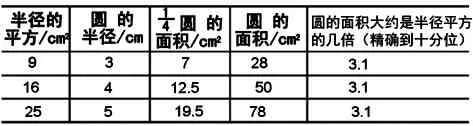
师：观察表格，你有什么发现呢？

生：我发现圆的面积大约是它半径的平方的3.1倍。

生：圆的面积大约是半径的平方的3 倍多一些。

师：据此，你又会提出怎样的猜想呢？

生：都是三倍多一点，这个数会不会就是圆周率呢？圆的面积会不会就是圆半径的平方的π 倍呢？

师：大家真了不起！下面我们就来验证这一猜想。

3.转化推导，经历验证过程。

师：同学们回忆一下，以前我们是用什么方法来推导平面图形的面积计算公式呢？

生：通过剪、拼、旋转等方法把新图形转化成已经学过的图形。

师：圆的面积计算公式是不是也能这样获得呢?

生：我们可以尝试一下，把圆转化成已经学过的图形。

师：好!要注意从哪儿下手剪拼最有可能转化成所学过的平面图形。

生：既然圆的面积和它的半径有关，我们想沿着圆的半径剪开。

师：究竟可不可以，我们来试试看。先把圆4 等分，谁来摆一摆？

学生操作如下（图6）：

图6

师：你还想把圆等分成多少份呢？（8 份）我们把这个圆平均分成8 份，再观察这个图形，你有什么发现呢？

学生操作如下（图7）：

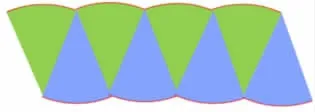
图7

师：你们也想自己动手拼一拼吗？老师在你们的材料袋里放了将圆16 等分的纸片，拿出来拼一拼，贴在《研学单》上。

师：从展示的几组由圆转化而来的图形中你发现了什么？

生：随着份数的增加，平行四边形的底这条曲线看起来就越来越直了。

师：想象一下，照这样再平均分下去会怎样呢？

生：拼成的图形会变成一个长方形。

教师课件演示把圆等分成（64 份、128 份、256份……），学生由衷地发出赞叹声（图8）。

图8

师：你有什么发现呢？谁来代表你们小组汇报一下？

生：长方形的长是圆周长的一半，用字母表示就是πr，长方形的宽相当于平行四边形的高，是圆的半径r。圆的面积公式就是：S=πr×r=πr2。

师：通过这个推导过程，验证了我们的猜想，那就是——

生：圆的面积果然是它半径的平方的π 倍！

师：“果然”一词用得真好。到目前为止，我们发现了圆蕴含着一个规律，圆的周长是它半径的2π倍，圆的面积是它半径的平方的π 倍。回想一下，我们是怎样探索圆面积的呢？

生：我们是从圆的周长是它直径的π 倍，推想圆的面积会不会也是直径或是半径的固定的倍数。

师：然后呢？

生：我们发现圆的面积除以直径或是半径不是一个固定不变的数，借助一个边长是半径的小正方形，我们发现圆的面积小于圆半径的平方的4 倍，而大于圆的半径的2 倍。

生：通过数格子计算得出圆的面积是它半径的平方的3.1 倍，我们就猜想圆的面积会不会是它半径的平方的π 倍。

师：再然后呢？

生：我们把圆转化成长方形，推导出圆的面积，从而验证了圆的面积果然是它半径的平方的π 倍。

师：我们在其中运用了推想、猜测、转化等探究数学问题的方法。

师：其实，16 世纪德国数学家开普勒就对圆的面积进行过深入的探究。

（课件视频介绍，图9）

图9

四、教后思考

在上面的教学过程中，教师首先组织学生猜测：圆的面积可能与什么有关系？学生一般会猜测圆的面积与半径或是直径有关系，这是不容忽视的事实。教师点拨：圆的周长除以它的半径或者直径的商是一个固定不变的数，那么，对于圆的面积你会有怎样的猜想呢？学生通过圆的周长计算的类比推理，自然而然地提出第一个猜想：圆的面积除以它的半径或者直径，是一个固定不变的数。学生再通过数格子的方式得出圆的面积，用圆的面积除以它的半径与直径没有得出一个固定的数。此时研究似乎走进了一个“死胡同”，教师的引导作用就充分体现了出来，组织学生观察圆的面积与那个小正方形之间的关系，学生很容易发现圆的面积与它半径的平方之间的倍数关系范围，提出了第二个猜想：圆的面积与它半径的平方之间的倍数会不会是一个固定不变的数呢？学生再用圆的面积除以它半径的平方，发现了商都是三倍多一点。提问：据此，你又会有怎样的猜想呢？学生提出了第三个猜想：圆的面积除以它半径的平方的商，会是一个固定不变的数吗？这个倍数是三倍多一点，会是圆周率吗？至此，学生三次提出猜想，在迂回中不断接近问题的本质。带着猜想，学生把圆转化成已知图形，从而推导出圆的面积公式，验证了猜想。学生经历了推想、猜测、操作、转化的过程，教师适时引导学生总结探索方法，授之以渔，从而促进推理等数学核心素养的提升。