怎样围面积最大——《用列举的策略解决问题》教学与反思

朱娇洁

【教学内容】

苏教版五年级上册第94 页。

【教学过程】

一、故事引入，提出问题

师：同学们，黑板上有一棵智慧树，但是现在大树上还没有长出知识叶，希望今天这节课学完以后，我们可以让这棵智慧树“枝繁叶茂”。

1.播放微课小视频，用“小欧拉智改羊圈”的故事激发学生思考，引入情境。

师：小欧拉到底是怎么做的呢？或许学完今天的知识可以对你们有点启发。

2.出示例题：王大叔用20根1 米长的木条围一个长方形花圃，怎样围面积最大？

活动一：

师：请一位同学读题，其他同学思考：从题中我们能得到哪些信息？

生：周长是20 米，围成的长方形的长和宽要是整米数。

师：长方形周长是20 米，根据这个条件，我们还能知道什么？

生：长加宽的和是10 米。

师：你能在脑海中想出一种符合要求的长方形吗？

师：再想想，只有一种吗？

二、动手操作，解决问题

活动二：

师：刚刚同学们都想到了几种不同的围法，要想知道怎样围面积最大，可以怎样做？

学生讨论后得出：要想知道怎样围面积最大，就要把不同的方法一一列举出来，计算面积后再进行比较，找到面积最大的摆法。

师：如果不想摆小棒，有更快的方法可以在《学习单》的空白框里写一写，与同桌交流。

1.把这张表格填写完整。

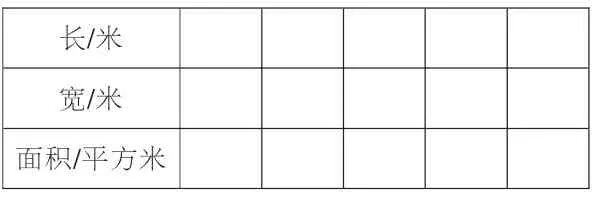
长/米宽/米面积/平方米

2.出示正确答案。

师：这位同学找到的摆法你有什么想说的？长是5 米，宽也是5 米的长方形对不对呢？为什么？

生：对的，因为长和宽都是5米说明这是一个正方形，正方形是一种特殊的长方形。

3.展示学生作业。

（1）比较有序排列和无序排列。

师：你更喜欢哪一种？为什么？

（2）展示不同方法：摆小棒、列表格、画图等等。

请学生上台介绍方法，并相机提问：你是从长是几米开始想的？为什么从长是9 米开始想？

生：因为长加宽的和是10米，那么长最长就是9 米，所以从9 开始想。

师：刚刚这几位同学的想法有什么相同点？

生：他们都是有顺序的。

师：对了，他们都是按顺序列出的，我们的知识大树上长出了第一片树叶。（树叶：有序列出）

师：为什么写到这里就不再往下写了？

生：因为已经列出所有情况了，后面的就开始重复了。

师：真棒！老师请这位刚刚说出关键字的同学上来画上第二片树叶！（树叶：所有情况）

师：你发现符合条件的围法一共有多少种？现在你们能告诉老师怎样围面积最大了吗？

生：长是5 米，宽是5 米。

师：同学们真厉害，最后我们只要比一比就不难看出面积最大的围法（树叶：比较），此时，我们围成了什么图形？

（3）出示错误、遗漏的情况。

师：你对这位同学的作品有什么想说的？

生：他最后一种写的是长4米，宽6 米，跟前面的重复了！

师：你观察得真仔细，那请你把你刚刚说的关键字写在知识树的树叶上。（树叶：不重复）

师：再看看这位同学的作品，你们发现了什么？

生：这位同学少写了一种情况。（树叶：不遗漏）

师：同学们，像这样有序地列出所有情况再进行比较就叫做一一列举，列举是解决这个问题的基本策略。（板贴课题：用列举的策略解决问题）

师：观察几个长方形中长、宽与面积的关系，你有什么发现？

（演示动态方格图，学生直观比较，小组交流讨论）

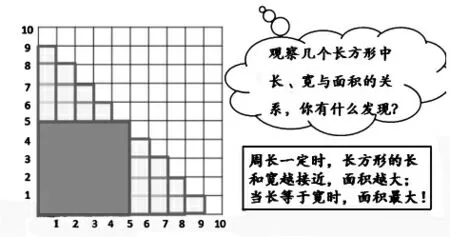
生：周长相同时，长方形长和宽的数值越接近，面积越大。当长等于宽时，面积最大！

师：现在你知道小欧拉是怎么解决这个问题的吗？100 米的篱笆围成的长方形面积最大是多少呢？

生：当围成正方形时面积最大，所以正方形边长是25 米，面积就是625 平方米。

师：同学们，闭上眼睛回顾一下我们刚刚解决问题的过程，你有什么体会？

（学生发言，教师相应板书“含义”“方式”“注意”）

师：回忆一下，在以前的学习生活中，我们曾经运用列举的策略解决过哪些问题？

生：10 以内的分与合、从条件出发解决问题。

三、课后总结

师：同学们，通过今天的学习你有哪些收获？你能像老师一样整理出属于你的智慧树吗？

【教学反思】

1.创设生活情境，激发学习兴趣。

首先在黑板上呈现了一棵“光秃秃”的知识树，引发学生的好奇心；然后给学生看了一段微视频，介绍数学家欧拉和他小时候的一个故事。引入本节课例1，我放手让学生独立思考解决问题，在学生比较自己的探究成果与同伴探究成果中，一步步加深提问。每当学生答出关键词后，如“有序”“不重复”“不遗漏”等，我都会让学生上讲台为知识树添加树叶，当新课讲授完后整棵知识树跃然于黑板之上，在视觉和思维上帮助学生加深理解。

2.探寻多种方法，发现规律。

当学生用自己的方法找出所有情况后组织交流，学生通过列表、画图、摆小棒、列算式等方法很顺利地解决了问题。然后我采用数形结合的方法，让学生观察动态的长方形演变图，在讨论后发现规律，即：周长不变，长和宽越接近，面积越大；反之，长和宽相差的越大，面积就越小。最后首尾呼应，回到本节课开头的故事引入，找到小欧拉围羊圈的方法。

3.回顾过程，总结方法。

通过提问“你有什么体会？”和“在以前的学习中，我们曾经运用列举的策略解决过哪些问题？”让学生知道其实在以往的学习中我们对列举的策略早有接触，体会列举是解决问题的有效方法，并逐渐掌握这种策略。