追根溯源，推动教与学的改进和发展——对一道『超纲』题的分析与反思

管小冬

数学期末考试刚结束，五年级数学组组长就向我反映，教师们认为试卷“解决问题”部分有一道题超纲了（题目如下），学校在组织阅卷时能否“手下留情”。

学校组织五年级部分同学到社区参加“迎端午”活动。分组情况如下：每组3 人，最后一组少2 人；每组4 人，最后一组少3 人；每组5 人，最后一组只有1 人。参加活动的最少有多少名同学？

教师们认为“超纲”，是因为这道题涉及“三个数的最小公倍数”和“同余”两个知识点，而课标、教材对此均未作要求。

考虑到评分标准需校际一致，所以最终阅卷时并未对这道题“手下留情”。但阅卷结束后，我第一时间就查阅了这道题的答题情况：全年级922 名学生，正确率73.3%，不高，但整体情况比教师们的预估要好。这一点其实也不难理解，这样的“超纲”题，在平时练习中也出现过，甚至还不止一次。只是，在翻阅试卷的过程中，学生们的解答过程引发了我对这道题及相关教学进一步的分析与反思。

一、为什么会这样？

翻阅中我发现，近乎所有学生，无论解答正确还是错误，过程都非常“简洁”且“一致”。以下是我摘录的学生的典型解答过程，其中图一为正确解答，图二为错误解答。

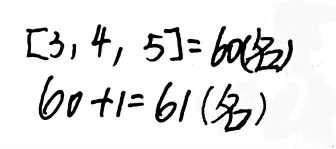
图一

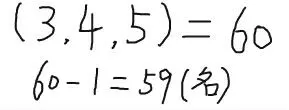
图二

显然，学生们在阅读、分析后，都是先求出3、4、5 这三个数的最小公倍数——60，然后再根据自己的理解做进一步的处理。错误大多出在对问题中“三数同余”的正确分析与理解上。但922 名学生中，仅3 名学生在解题时使用了列举的方法，且都出现了错误。这有些出乎我的意料。

我们知道，在“公因数和公倍数”这部分内容的教学中，几个版本的教材都是引导学生通过列举找出两个数的公因数或公倍数，借此进一步理解公因数和最大公因数、公倍数和最小公倍数的含义。那么，是什么原因导致学生在解题时鲜用列举法呢？那些解答过程特别“简洁”的学生，是在草稿本上列举了？还是有别的原因呢？

为此，我在学校执教过五年级的教师中进行了一次问卷调查。问题如下：

问题一：在公因数、公倍数相关内容的教学中，你重点指导学生使用的是什么方法？

问题二：你教过学生如何求三个数的最小公倍数吗？重点指导的是什么方法？

共37 位教师参加了问卷调查。问题一中，37 位教师均提到了列举法与短除法，但33 位教师重在使用短除法，仅4 位教师重在使用列举法；问题二中，37 位教师均教学过如何用短除法求三个数的最小公倍数，其中10 位教师还介绍过列举、大数翻倍等其他方法。

在随后的访谈中我发现，不少教师都经历过旧版本教材的教学，那时“分解质因数”“短除法求最大公因数、最小公倍数”等都属教材内容。教材改版后，虽删减了这部分内容，但教师们在教学中都会自觉补上。显然，教师们大都没有很好地理解教材删减这部分内容的原因。对此，北师大版教师用书上明确指出，“‘短除法’虽高效简便易用，但技巧性较强，学生不易理解其算理，容易形成机械性练习，故此将之放到‘你知道吗？’板块中，学生做一般性了解即可。”这样的编排，也是重在引导学生进一步掌握“列举”这种常见的解决问题的数学思考方法，并在此过程中不断增进对公因数、公倍数相关知识的概念性理解。而在实际教学中，教师们不但着重补充介绍了“短除法”，甚至将之作为解决这部分内容相关问题的最佳方法进行了强化指导。进而就忽视、弱化了学生对“列举”这一常用方法的体验、理解与掌握。

如此，仅3 名学生在解决上述问题时使用了列举法，且都出现了错误，其原因不言而喻。正是教师们“超纲”地教，“过度”地教，导致了学生们过早、过“充分”地感受到了短除法的“易学易用”，进而抛弃了“过程繁琐”的列举，转投短除法的怀抱。

由此，当学生遇到上面这道“超纲”题时，最直接的反应便是先要求3、4、5 这三个数的最小公倍数，无形中弱化了对问题中数量特征、相互关系的深入思考，进而导致出现错误。

二、这道题“超纲”了吗？

从教与学的角度分析了上述题目出错的原因后，我又仔细地翻阅了人教版、苏教版、北师大版等几个版本的数学教材。再次学习之后，一个追问在我脑海中悄然浮现：这道题“超纲”了吗？

按我们惯常的理解，“超纲”是指题目超过了教学大纲的要求。“大纲”是课改前的说法，对应当下应该是指《义务教育数学课程标准（2011年版）》（以下简称“课标”），这是各版本小学数学教材编写时的指导与依据。“课标”对这部分内容的要求，主要有两点：1.了解公倍数和最小公倍数；2.能找出10 以内两个自然数的公倍数和最小公倍数。显然，这两点主要是从基础知识与基本技能的维度提出的要求。对照这样的要求，这道题出现在期末考核中显然是超纲了。

但继续查阅课标及各版本教材，我发现，小学阶段学习“公因数与公倍数”这部分内容，更多是服务于后续的分数四则运算。即学生在进行分数四则运算时涉及到的通分与约分，均涉及公因数、公倍数的相关知识与技能。同时，通过对后续小学及初中数学教材的查阅，我还发现：1.三个数的公倍数、最小公倍数均未作为正式教学内容在后续教材中出现过；2.与此相关的分数加减运算，教材呈现的例题与练习中，三个异分母分数中总有两者的分母是倍数关系。如苏教版五年级下册第五单元“分数加法和减法”例2后的“试一试”即为在义务教育阶段的数学教材中，“同余”从未作为教学内容出现过。

对此，我又进一步思考，究竟什么是“超纲”？如果只是因为解决问题中涉及到的相关知识、技能从未作为正式教学内容在教材中出现过，便可称之为“超纲”，那教学的意义与价值何在？学生在数学上的发展何在？往更深远处思考，数学发展、社会进步、文明日新月异又该从何谈起？

如果我们暂时抛弃紧守的基础知识与基本技能，从基本思想感悟与基本经验积累的角度来看待这道题，那便会发现其实它也谈不上“超纲”。因为，从解决问题的角度来看，这道题恰可考查学生能否使用合适的方法寻找出契合题意的答案，而非考查其是否掌握了“三个数的最小公倍数”及“同余”相关的知识与技能。

我想，如果教师们没有重在“超纲”教学，而是侧重于指导学生掌握列举这一常用的解决问题的方法，侧重于引导学生思考、交流如何根据题意优化列举过程，那么，当上述题目出现时，教师们反映的将不再是“这道题‘超纲’了”，而是“我的学生一定行！”。

三、后续教学如何改进？

分析至此，我想，最重要的还是“在后续教学中，我们应该如何改进”。以下是我的一些思考，与大家分享，希望能起到抛砖引玉之效。

1.重视在基本方法的运用中积累经验、深入思考。

很多时候，作为教师的我们在教学中往往会自觉或不自觉地突出一些数学的公式、定理、算法。因为只要学生掌握了，带来的便是解决问题的高效。然而，正如曹培英老师所强调：“只知怎样算，不知为什么这样算，充其量只是搬弄数字的操作技能。”我们应该充分认识到，对学生而言，更重要的是在基本方法的运用过程中不断积累数学活动经验，深入数学思考。小学阶段，读题、分析数量关系、画图、列举等等，都是学生应掌握并乐于使用的基本方法，也都是我们应重视的。

以“公因数和公倍数”部分的教学为例，教学中我们更应突出引导学生在理清问题要求的基础上，就“如何正确列举”“怎样优化列举过程”等问题展开思考与交流。在这样的过程中，进一步增进学生对基本概念的理解，对“列举”这一基本方法的价值认同。同时，应避免如“短除法”之类的相关算法的提前出现与过度教学。因为，这往往会导致学生不加思考地理解与运用。更因为，对于学生的数学学习而言，经历过程、学会思考要远比掌握一种虽简洁却不甚理解的方法重要得多。

回到期末试卷中的那道题，我想，作为教师的我们，更应期待学生能够呈现出以下思维状态：（1）在审视问题后，确定可以通过列举寻找到正确答案；（2）根据题意，或一一列举，寻找答案；或思考怎样列举更便捷高效；（3）得出答案后，作进一步的审视与反思，确定答案是否正确，并能根据发现的错误及时进行调整。因为，解决问题没有“通法”，数学知识的深度理解、解决问题能力的不断提高，有赖于学生在基本方法运用过程中积累经验与深入思考。

2.重视在解决问题的过程中培养反思、 质疑等良好的学习习惯。

从前文呈现的图二中我们可以发现，学生在求出3、4、5 的最小公倍数60 后，仅仅是根据自己的理解，再将60 减去1，便不加甄别地认为这就是正确答案。在3 名使用列举法解决问题的学生中，也出现了类似情况（如下图）。

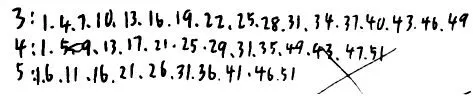
显然，前者缺少答案得出后需及时进行检验的意识，仅仅满足于获得答案；后者更是在列举未能找到符合要求的答案后不了了之。其实，稍加回顾与反思便会发现：（1）第二行在列举到29 后，出现了错误；（2）只要列举过程无误，继续列举下去便能找到符合要求的答案。但两者恰恰都缺少了这样的意识与习惯。

试想，如果学生初步具备了及时检验、反思、质疑等良好的学习习惯，那么，在遇到类似的题目时，也能在获取初步答案后，经由检验、反思、质疑等环节形成自己的初步判断，并借此获得更为深入的思考与领悟。而这种基于过程，经由深入思考、分析所获得的收获与发展，也将促成学生在经验积累、数学思考等方面更进一步的发展。

以上是基于对学生错误解答过程的审视而获得的启示。虽然我们一直都在强调培养学生反思、质疑等良好的学习习惯，但显然做得还不够。教学中，我们应引导学生充分认识结果检验、过程回顾、反思质疑等环节的作用与价值，使之成为其解决问题过程中的自觉行为。

3.重视从素养发展的角度进行命题设计。

除从“教与学”的角度进行分析与反思外，我们也应从如何更好地进行数学命题设计这一角度进行反思，使考核不仅具备评价功能，更能推动学生数学素养的进一步形成与发展。

就这道期末考题而言，在问题呈现后我们不妨增加如下几个引导环节：（1）你能根据题意，使用列举的方法解决这个问题吗？（2）回顾你的列举过程，再结合题目想想，有哪些地方列举得可以再简洁些？（3）你得出的答案正确吗？试着在下面进行检验。（4）通过检验，你发现“每组3 人，最后一组少2 人；每组4 人，最后一组少3 人；每组5 人，最后一组只有1 人”这些不同说法之间的联系了吗？

如此，将这道题从教师们认为的知识与技能“超纲”，转为对学生使用列举这一基本方法解决问题、对所得答案进行检验、对解决问题过程进行回顾与反思等多方面能力的考查与评价。同时，也使评价兼具了引领学生积累数学学习经验，促成数学思考发展的功能。

以上是我对期末一道“超纲”题的分析与反思。一道题似乎微乎其微，但只有我们真正从教与学的角度出发，不放弃对每一个问题的追根溯源，坚持以成因剖析推动教与学的改进和发展，方能积少成多，聚沙成塔，使每一位学生都能在数学上获得更好的发展。