在合理推想与完整建构中提升课堂品质——以《小数的意义》教学为例

朱秋虹

【课前思考】

本课教学应让学生充分体验小数的产生过程，在形象操作与合理推想中推进教学。同时，让学生经历“数”概念抽象的一般过程，获得有效的方法体验，提升学生数学学习的品质。

在具体教学过程中，应立足“教会学生想”，从一位小数的意义起，让学生完整表达自己的想法，到两位小数的意义，让学生能将“想的方法”进行结构迁移，再自主推想到三位小数的意义。让学生在自己的思考与表达中，学会归纳、概括，自主建构新知。

首先，结合米尺的产生过程感知小数产生的需要及小数的计数单位产生的过程，从而理解小数的意义。其次，抓住从“具体的量”的认识转向对“抽象的数”的意义的理解，从学生熟悉的有单位的长度、价格、质量，到无单位的图形中的小数及数轴上的小数，让学生经历数的概念抽象的一般过程。

【教学过程】

一、复习一位小数，初步感知一位小数的意义

1.引入。

出示：1 米长的纸条，用纸条去测量练习册的长。

提问：练习册的长有1 米吗？估计一下，大约是几米？（0.3 米）0.3 是一个小数，这样的小数是怎样产生的？能结合1 米长的纸条来说一说吗？

提供帮助，出示被平均分成10 份的纸条米尺：

小结：把1 米平均分成10份，其中的3 份，就是0.3 米。因为1 米=10 分米，所以3 分米是1 米的，3 分米=米=0.3 米。

2.练一练。

提问：1 分米和6 分米的点，说说用分数和小数表示分别是多少？

3.读一读，数一数。

引导：上面的每一个点都可以用分数或小数来表示吗？自由地读一读这些分数和小数。

提问：结合纸条米尺想一想：1 米里有（）个0.1 米？

4.说一说。

提问：这些小数是怎么来的？

小结：因为把1 米平均分成10 份，才得到分母是10 的分数，可以写成这样的小数。

（板书：1 米 平均分10 份）

【设计意图：结合纸条米尺进行数数，初步抽象，感知数轴上的点。在数的过程中感受小数的序列，感知1 米里有10 个0.1 米。】

二、认识两位小数，理解两位小数的意义

提问：用纸条米尺测量练习册的宽，你发现了什么？0.2 米多一些，又不到0.3 米，到底多长，怎么解决这个问题？

更新纸条米尺：把0.1 米再平均分成10 份，也就是把1 米平均分成100 份，每份是1 厘米。

1.小组研究。

出示要求：看着米尺想一想，1 厘米等于几分之几米？用小数表示是多少？说说你们是怎么想的？

2.迁移练习。

（1）跟同桌说说练习册的宽。

提问：练习册宽几厘米？是1米的几分之几？是几分之几米？写成小数是多少？

要求学生能完整表述：如1米=100 厘米，21 厘米是1 米的，21 厘米=米，可以写成0.21 米。

（2）自主练习：米尺上找一个点，先说说是几厘米，再让同桌用刚才的方法说一说，写成分数是多少，小数是多少。

3.对比归纳。

师：观察现在的这些分数和小数，跟刚才说的有什么不一样？

（分母是100 的分数，小数点后面有两位）

（介绍两位小数和一位小数）

4.数一数。

提问：看着米尺，你能从0.01米数到0.10 米吗？发现了什么？

小结：0.10 米里有10 个0.01米，1 米里有100 个0.01 米。

推想：这些两位小数是怎样产生的？

（将1 分米再均分10 份，1米均分成100 份）

小结：把1 米平均分成100份，得到了许多分母是100 的分数，这些分数可以写成两位小数。

引导：刚才我们认识了一位小数、两位小数，这时你想到了还会有……

（学生举例三位小数，如0.001米，0.039 米）

【设计意图：结合纸条米尺制作过程，经历两位小数产生的过程，感受两位小数产生的需要。从一位小数与分数的联系去感知两位小数与分数的关系，理解其意义。】

三、合理推想，迁移认识三位小数的意义

1.同桌观察米尺进行讨论。

提问：在米尺上找到你说的这个三位小数，跟同桌说一说，你是怎么想到的？

练习：140 毫米，用米作单位是多少呢？

2.推想。

提问：你还会像刚才那样来数一数这些三位小数吗？推想一下1 米里有几个0.001 米？

4.回顾小结。

提问：对比你们的米尺和黑板上的1 米纸条，说一说这1000份是怎么分出来的？

（将1 厘米再均分10 份，1米均分成1000 份）

师：如果继续推想，你想到了什么？

【设计意图：在前两次的教学基础上，学生自然而然地推想到三位小数的意义，从制作纸条米尺转向结合实际的米尺去推想制作过程，感受将1 厘米再平均分成10 份，每份是1 毫米，也就是将1 米平均分成1000 份，得到了千分之几可以写成三位小数。】

四、拓展对比，建立小数的内在含义

过渡：米尺上的几分米、几厘米、几毫米用米作单位时都可以用小数来表示，那么3 角、2 角9分、49 千克，换一个单位是不是也可以用小数来表示呢？

1.拓展到其他的数量。

交流：填的时候你是怎么想的？2 角9 分和0.29 元这两种表示方法，你喜欢写哪一个？

小结：把1 元平均分成100份，每份就是1 分，所以几分也就是1 元的百分之几，写成两位小数。把1 吨平均分成1000 份，每份是1 千克，有几千克，也就是1吨的千分之几，写成三位小数。我们发现用小数来表达更为简洁。

2.抽象到将“1”平均分。

引导：将1 米、1 元、1 吨进行平均分，可以得到许多小数，那如果是“1”呢？用正方形或正方体表示整数“1”，涂色部分可以用小数表示出来吗？

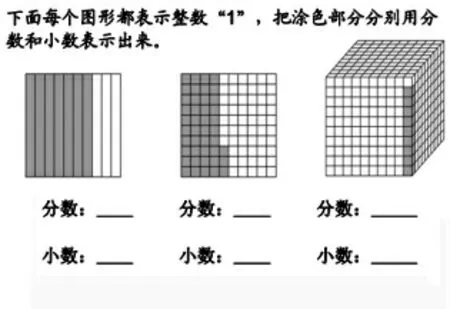
3.归纳小数的意义。

提问：小数是怎么来的？它与什么有关？一位小数、两位小数、三位小数分别表示什么意义？

小结：知道小数是怎样产生的，就知道了小数的意义。十分之几、百分之几、千分之几……可以写成一位小数、两位小数、三位小数……

【设计意图：这既是丰富学生的学习素材，更是一种学习情境的变化和学习能力的迁移。从长度单位转向其他的单位，从具体的量到正方形，逐步抽象，从而形成对“抽象的数”的意义的理解。】

五、全课小结，巩固提升

1.数轴上的小数。

（1）数轴上标上0、1，让学生找出0.8 和0.08。

提问：上面有小数吗？0.8 大约在哪里？怎么确定他指的是否正确呢？

（根据学生回答，把1 平均分成10 份，0.8 就是十分之八）

提问：0.08 大约在哪里？为什么？在0 和1 之间你可以找到几个小数？

（2）数轴上标出2，引出比1大的小数。

提问：这个点大约是多少？它跟我们刚才说的小数有什么不同呢？

小结：除了整数部分是0 的小数，还有许多小数的整数部分是1、2、3……比1 大的数。

2.生活中的小数。

（1）手机长（）。A.0.9 米 B.0.09 米 C.0.009 米

（2）生活中的1.555 升是多少？

（3）一粒药片0.15 克，表示什么意思？

【设计意图：结合数轴上的数及生活中的小数让学生进行估计与分析，发展数感，同时也再次考量学生对一位小数、两位小数、三位小数意义的理解。由此，将小数的认识纳入学生原有的知识结构，同时也延伸到后续的学习探究活动中。】

【教后反思】

小数是学生生活中接触比较多的一类数，理解和掌握小数的意义有助于学生运用数学知识去分析与解决生活中的现象和问题。

1.把握知识本源，铺陈教学内容。

小数的本质是十进制分数的一种表现形式，它的产生基于生活实际的需要——当整数无法帮助人们顺利完成生活中的计量时，小数就产生了。正是由于小数就是十进制的分数，它和整数计数系统是统一的。因此，在教学中既关注小数与分数的内在联系，又引导学生感受小数与整数一样蕴含“十进”“十分”关系。安排了测量情境，在情境中让学生体验小数产生的需要。这样的安排有利于学生发现数学的实际价值，学会用数学的方法解决问题。

小数在形式上就是分母是10、100、1000……的分数改写而来。这种小数与分数之间形式上的联系，既体现了小数的本质意义，又给学生提供感知的抓手，教材内容的编排也充分运用了这一联系。教学中紧密结合小数与分数之间形式上的联系组织教学内容，逐步将学生对小数意义的理解引向深入。

2.启迪学生合理推想，展开教学过程。

教材安排学生在两次认识分数后逐步认识小数的意义，其目的就是合理降低学生体验小数意义的难度。分数是“数与代数”知识中形象与抽象的飞跃，学生对于分母是10、100、1000……这样的分数很难用形象的操作去体验，计量与计量单位换算的引入有效克服了这一挑战，让学生在单位进率的基础上有了推想的依据。这种半形象半抽象的操作与推想符合中高年级学生的思维能力，是学生“跳一跳”可以实现的。因此在教学中让学生经历了米尺上分米、厘米、毫米的构造过程，帮助学生理解操作中三次平均分的内涵，从而为相应分数的产生打下推想的基础。

有了分数的铺垫，学生对于相关小数演变的推想就成为了必然。此时结合学生生活经验安排比较小数形式的发展，让学生在一般逻辑的指引下从一位小数推想到了两位小数、三位小数、四位小数……这样的教学活动组织有利于发挥学生学习的主动性，在活动中不断收获成功的体验，逐步完成对小数的意义的整体感知。这样的感知不仅提升了学生的数感，还培养了学生逻辑推理的能力。

3.经历概念抽象过程，形成知识的自我建构。

小数的概念最终是抽象的结果，学生只有在多层次的体验基础上，逐渐脱离感知中所依赖的现实对象才能完成抽象概括。在教学中，首先让学生在长度计量和单位换算中初步体验小数的产生过程；接着组织学生在人民币单位、质量单位等换算中进一步体验小数与十进制分数之间的内在联系；而后启发学生将图形看成整数“1”进行平均分得到相应的分数和小数，让学生经历“具体的量”的认识到“抽象的数”的意义的过程，逐渐摆脱对计量单位以及进率的认知依赖；最后引导学生对小数的意义进行抽象的概括。这一过程体现了数学概念学习的一般规律，为学生今后的数学概念学习奠定了基础。

为了帮助学生顺利完成最终的抽象概括，用“这样的小数是怎样产生的”这一大问题引导学生在每一个学习阶段进行有意义、有目的的反思，最后用“知道小数是怎样产生的，就知道了小数的意义”这样的总结性提示，帮助学生在第一时间将知识抽象整合，实现对小数意义的完整建构。