球载临近空间载荷服务舱的动力学分析

田春敏，黄 旻，钱路路

（1.中国科学院计算光学成像技术重点实验室，北京100094；2.中国科学院光电研究院，北京100094；3.中国科学院大学，北京100049）

1 引言

临近空间一般指高度位于（20～100）km 的空域，是指介于航空与航天空域之间的一个特殊位置。由于临近空间位置的特殊性[1]，近年来世界各国愈加重视其开发与利用。随着临近空间飞行器的飞速发展[2-3]，越来越多的设备正不断应用于临近空间中。临近空间载荷服务舱正是在临近空间中完成相应科学任务的。

临近空间载荷服务舱是光机电一体化设备，它会搭载高空气球到达临近空间进行科学实验。为了保障科学实验的后续处理，载荷服务舱在临近空间中完成科学任务后会以特定的速度返回地面，考虑到在落地的瞬间，与地面的碰撞会对载荷服务舱的稳定性有影响。因此，为了回收载荷服务舱内相关设备，需要对载荷服务舱落地时的安全性进行分析，这里采用有限元的方法对载荷服务舱进行力学分析。首先简要介绍了载荷服务舱的结构设计，分析了建立有限元模型的外部条件，然后利用ANSYS workbench 对临近空间载荷服务舱进行动力学分析。其中，重点在于分析落地时减震机构的力学性能，给出了有限元分析出的结果，其分析结果对于临近空间载荷服务舱的回收具有指导意义。

2 载荷服务舱的结构

临近空间载荷服务舱是由主舱体、下投式探空仪、减震拉杆、减震器、减震底座、天线模块和探空箱构成的，如图1 所示。载荷舱主舱体内设有上下两层，其中包括电源模块、热控模块、数据传输设备、探空载荷等部件，在主舱体的上方还承受来自外界的100kg 的载重。为了保障主舱体内部设备的安全回收，这里设计了减震装置，该装置能有效减小主舱体落地时所受到的冲击作用。为了确保减震装置的真实有效，重点对减震装置的力学性能进行分析

图1 临近空间载荷服务舱模型Fig.1 The Model of Load Cabin in Near Space

3 力学模型

载荷服务舱的力学分析主要利用ANSYS Explicit Dynamics模块，这里是运用显示动力学有限元方法来进行分析求解的，其基本方程[4]为：

式中：M—质量矩阵；C—阻尼矩阵；F—内力矢量；R—外载荷矢量；—节点速度和加速度矢量。

在ANSYS Explicit Dynamics 模块中采用显示算法中的中心差分法对运动方程进行积分求解。在此方法中，任意t 时刻的速度矢量和加速度矢量可以用位移u 来表示：

将式（2）、式（3）代入到式（1）中，则可以得到这种算法的各个时间点的递推公式为：

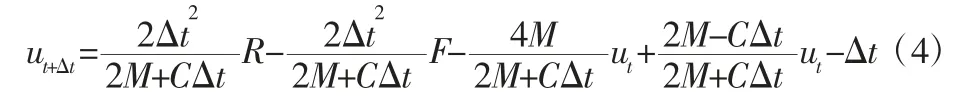
式（4）表明只要设置合理的初始分析条件，利用此方法是可以求解出每个离散点的位移值。因此采用此方法对临近空间载荷服务舱进行动力学分析，通过前期对载荷服务舱的特征属性分析，设置合理的初始条件，从而得出真实有效的仿真数据。

4 有限元模型的建立

有限元方法的基本思想是将结构离散化，用有限数量的简易单元来表示复杂的对象，单元与单元之间通过结点连接，再根据边界约束条件来综合求解。由于方法中的单元和结点的数量是有限的，所以称之为有限元方法。这种方法中单元之间组合方式灵活多变，并且单元本身又可以有不同形状，比如四面体、六面体等，因此在实际中可以对几何形状不规则的模型来进行模拟求解[5-7]。

采用有限元的方法对载荷服务舱进行力学分析，是将载荷服务舱内部结构离散化，划分为有限个单元，主要是对载荷服务舱主体结构进行单元格的划分，其中主要涉及载荷服务舱主舱体和减震结构，然后通过ANSYS 软件对载荷服务舱落地安全性进行仿真求解，得出载荷服务舱变形情况和应力分布情况。

4.1 简化模型

为了仿真实验的有效性和准确性，首先对于其中载荷服务舱的舱体进行简化处理，保留主体框架结构，简化舱内外箱体设备，以质量点代替，封闭模型通孔。既保证分析载荷服务舱下落过程时惯性力的准确性，也减少仿真分析时的计算量。在减震拉杆下部的减震器简化为弹簧，其刚度系数大小设为107N/m。载荷服务舱简化后的模型，如图2 所示。

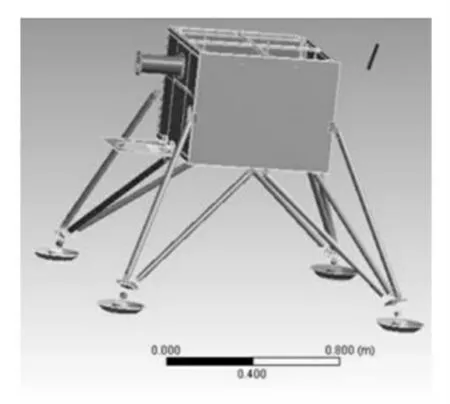
图2 载荷服务舱简化模型Fig.2 The Simplified Model of the Load Cabin

4.2 材料特性

考虑到系统整体重量的要求，这里基本材料设定为镁合金。其中，减震器的材料设定为45 钢，而对于载荷舱主舱体下方的减震拉杆，可采用碳纤维T800 这种高强度新型材料。其余未加说明的均按照镁合金来分析。碳纤维是一种含碳量在95%以上的高强度、高模量纤维的新型纤维材料。它是由片状石墨微晶等有机纤维沿纤维轴向方向堆砌而成，经过碳化处理而得到的微晶石墨材料。碳纤维密度小，强度高。同等条件下，质量比铝轻，但强度比钢铁还要高，因此在国防军工和民用方面都是重要的材料[8-10]。考虑到本次科学实验的特殊性，此载荷服务舱将搭载高空气球前往临近空间进行高空实验。实验结束后载荷服务舱将以一定的速度自行下落至地面。考虑到下落后与地面碰撞的剧烈，这里采用碳纤维复合材料，既能满足高空中实验需要尽量降低重量的要求，也能满足高强度的要求。为了更加准确地仿真载荷舱下落时减震装置的力学性能，以下给出载荷服务舱的组成部件的材料及其部分参数，便于后续准确地进行仿真分析。材料特性参数对照表，如表1 所示。

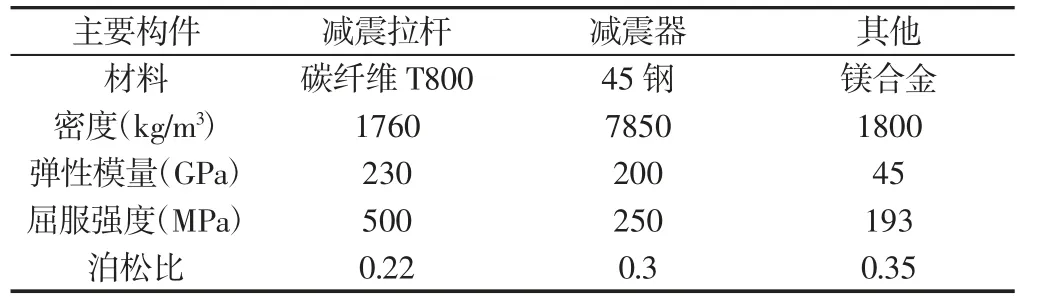
表1 材料特性参数对照表Tab.1 Material Characteristic Parameter Table

4.3 约束条件

为避免载荷服务舱在临近空间的科学实验后落地时载荷服务舱体发生剧烈碰撞而导致设备损坏，将利用有限元的方法针对载荷服务舱的拉杆模型进行力学仿真。主要是针对落地时冲击响应的仿真分析。对于载荷服务舱的力分析条件，通过实际工况条件分析，得出以下几点：（1）速度：给物体一个初始速度，是动力学仿真的常见约束条件。载荷舱服务舱就设定有初始速度。（2）重力加速度：在载荷服务舱下落的过程中，由于地球引力的作用，需要添加重力加速度以尽可能逼真地反映下落情况。（3）力和加速度：在这里，将载荷服务舱内外部分设备简化为质量块，作为底板的受力条件，即以等效力代替原来的结构。通常力和加速度也是需要求解的自由度。（4）接触关系：接触关系有绑定接触、摩擦接触、无摩擦接触等关系，根据实际情况，这里从理想情况考虑，即各结构不分离，因此分析中采用绑定接触。

5 有限元分析

5.1 边界条件

根据前面对于载荷服务舱模型，如图3 所示。可以得出软件中设置的边界条件参数有：（1）载荷服务舱以重力下落，并以7m/s速度冲击地面；（2）载荷服务舱上表面负载100kg；（3）舱内设备均简化为质点，作为重力施加于承载面上；（4）设置固定约束，分析时间设为3s，步长为自动控制。

图3 有限元边界条件Fig.3 The Finite Element Boundary Conditions

5.2 仿真实验

5.2.1 网格划分

对载荷舱进行网格划分，网格后的有限元分析模型，如图4所示。网格划分后，产生1082108 节点，2809324 个单元，可满足冲击分析的需要。

图4 网格划分模型Fig.4 The Model After Meshing

5.2.2 仿真结果及分析

根据前面有限元模型的分析，可以得到有限元仿真的结果。首先对于载荷服务舱整体变形进行分析，得出结果，如图5 所示。由图可知载荷服务舱最大变形为0.67551mm，变形较小。对于变形后的载荷服务舱，为了更加准确地判断其力学性能，在此对其进行应力分析。载荷服务舱舱体整体应力分布云图，如图6 所示。其中，最大应力为384MPa，出现在底座与地面接触的区域。载荷服务舱舱体及减震装置的应力均不超过170MPa。载荷服务舱下侧的减震拉杆的应力分析云图，如图7 所示。由图可知，减震拉杆中最大应力为71198Pa。综上可知，最大应力发生在底座与地面接触的位置，其大小为384MPa，超过镁合金的屈服强度，发生不可恢复变形。但考虑其影响，载荷服务舱舱体应力小于193MPa，即小于镁合金的屈服强度，因此载荷服务舱舱体的变形是在材料允许的变形范围内。最后，仿真实验中减震拉杆内的应力均小于72MPa，远小于小于碳纤维T800 的屈服强度500MPa，因此在落地过程中减震拉杆能很好地发挥减震性能，保障载荷服务舱安全落地。

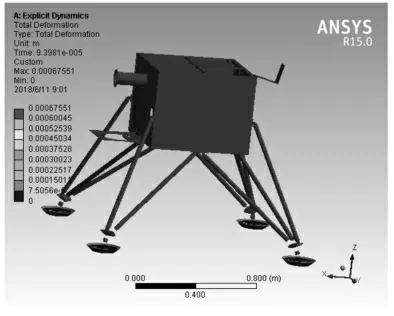
图5 载荷服务舱总体变形云图Fig.5 Total Deformation Nephogram of Load Cabin

图6 载荷服务舱应力分布云图Fig.6 Stress Nephogram of Load Cabin

图7 减震拉杆应力分布云图Fig.7 Stress Nephogram of Shock Absorber Linkages

6 总结

通过对载荷服务舱落地时受到的冲击的过程的仿真，得出了载荷服务舱以7m/s 的速度下落并与地面的碰撞后的形变和应力分布。由结果可以看出，载荷服务舱主体结构并没有因为受到冲击而被破坏，载荷舱结构总体上稳定可靠。主要减震结构能很好地承受地面冲击，为载荷服务舱安全落地提供了保障，有利于载荷服务舱内部分设备的安全回收，为临近空间科学实验奠定了基础。