飞机发动机吊挂多目标拓扑优化研究

苏长青，杨 蕾，郝万里，邓 庆

（1.沈阳航空航天大学安全工程学院，辽宁 沈阳 110136；2.胜利油田物华管业有限公司，山东 东营 257500）

1 引言

随着经济发展和科学技术的不断提高，飞机性能逐步提升，结构更加复杂，承受载荷越来越大。飞机发动机吊挂作为重要的承载和连接装置，既要传递动力，还要承受发动机及飞行过程中自身产生的载荷，是全机的高温影响区和集中受力区。因此，发动机吊挂要具有较高的强度和可靠性。飞机的重量对飞行性能有直接影响，结构优化可以大大减轻结构重量，在保证机械性能的前提下对飞机发动机吊挂进行结构优化，寻求材料最佳布局，不仅可以节约成本，还可以提高飞机的飞行性能。

目前连续体拓扑优化主要集中在单目标拓扑优化，吊挂模型结构在多工况环境中工作，每种载荷工况会产生不同的最优刚度拓扑优化结果，为解决此问题，可以将静态度工况拓扑优化问题即可转化为多目标拓扑优化问题。有关飞机发动机吊挂拓扑优化的研究大多将多工况问题转化为单目标问题。科研人员将多工况下的加权应变能作为目标函数，进行吊挂结构拓扑优化；科研人员采用加权组合将多目标问题转化为单目标优化，多工况下以结构柔度的加权最小为目标函数建立优化模型，并进行灵敏度分析。这两种结构优化均未考虑吊挂的动态振动性能和飞行过程中冲击载荷的作用，很难得到最优的拓扑优化结构。采用有限元分析软件，在现有的盒式梁式结构吊挂的基础上，进行飞机发动机吊挂的拓扑优化。选择带惩罚系数的变密度SIMP 插值法，以吊挂整体柔度和固有频率为目标函数，约束位移和体积，用移动渐近线法作为优化算法。在吊挂拓扑优化设计中，结合各工况设计载荷，采用带权重的折衷规划法进行拓扑优化，得到满足静态多工况下刚度最和和动态振动频率最大要求的吊挂拓扑结构。

2 多工况刚度和固有频率要求的拓扑优化目标函数

拓扑优化方法中最常采用变密度法，将结构的拓扑优化问题转换为材料的最优分布问题。变密度法中常用的插值模型SIMP 是一种带惩罚因子的相对密度法，计算效率高，应用广泛。

结构多目标优化以体积和位移为约束，优化目标同时满足模型多工况静态刚度和平均振动频率的要求，采用折衷规划法得到多目标拓扑优化的综合函数：

式中：F（ρ）—综合目标函数；w—柔度目标函数的权重；wi—第i 个工况的权重系数；ci（ρ）—第i 个工况的柔度目标函数—第i 个工况柔度目标函数的最大值和最小值；Λ（ρ）—固有频率目标函数；Λmin、Λmax—频率函数的最小值和最大值。

对模型进行结构优化时，若将几个低阶频率作为目标函数，几阶频率相互影响，有些到达频率波峰，有些则会降到较低值，很难同时达到频率最大值，为了克服此问题，采用平均频率公式来定义固频率拓扑优化的目标函数：

式中：Λ（ρ）—平均功率；λk—第k 阶特征频率；λ0、s—给定的参数，用来调整目标函数；wk—第k 阶频率的权重系数；f—需要优化的低阶频率的阶次。

多目标拓扑优化综合函数中，对于每种工况权重系数的确定，传统方法是设计者根据设计经验给出每种工况的重要程度值，此时的权重系数为定性判断值，无法精确，存在较大误差。为解决上述问题，参考运筹学的层次分析法，构建一个决策矩阵A=（aij）n×n，n 代表决策的数目（这里为工况数目），将i 和j 工况两两配对比较，aij为要素i 和要素j 重要程度比较结果。决策矩阵可以写成：

决策矩阵的特征向量即为各工况所对应的权重系数。

其中，aij的数值参考，如表1 所示。

表1 配对决策矩阵重要性比值Tab.1 Pairing Decision Matrix Importance Ratio

根据层次分析法确定权重系数时，决策矩阵的一致性检验是不可或缺的一节。为了度量决策矩阵是否满足一致性要求，Saaty 定义了一致性指标。

式中：CI—一致性指标；

λmax—矩阵的最大特征值；

n—矩阵阶数。

当CI=0 时，决策矩阵完全一致，CI 越大，不一致程度越大。Saaty 引入了一致性比值CR 确定不一致程度的接受范围，当阶数大于2 时，若一致性比值。

则一致性可以接受。

式中：RI—随机产生矩阵的一致性指标，如表2 所示。

表2 随机矩阵一致性指标RI 参考值Tab.2 The Reference of Random Matrix Consistency Indicator RI

3 多工况综合目标飞机发动机吊挂拓扑优化设计

3.1 有限元模型的建立

将盒式梁式结构吊挂导入有限元分析软件中进行预处理，定义材料为7050 铝合金板，采用四面体网格进行划分，有限元建模，如图1 所示。

图1 飞机发动机吊挂的有限元模型Fig.1 The Finite Element Model of Aircraft Engine Pylon

在吊挂的前接头、后接头和剪切销柱孔施加约束。根据吊挂在不同飞行状态下，承受载荷最大的三种工况，即两种应急着陆和侧移，在前、后安装架分别施加载荷，根据总过民航总局制定的运输类飞机适航标准条例，得到发动机吊挂包络载荷、数值，如表3 所示。

表3 发动机吊挂包络载荷Tab.3 Engine Pylon Envelope Load

将表3 中发动机吊挂包络载荷折算到吊挂前后安装架下表面中心点，得到载荷，如表4、表5 所示。

表4 吊挂前安装架所受载荷Tab.4 Load of Pylon Front Mounting Bracket

3.2 确定加权和目标工况

借助软件中用户自定义方程来定义多目标拓扑优化的目标函数，将其作为一个目标响应，关联多种工况。综合目标函数式，如式（1）所示。

对飞机发动机施加的静态载荷工况为应急着陆1、应急着陆2 和侧移三种工况，n=3，参照表1，对工况重要度进行两两比较。得到工况重要度决策矩阵：

矩阵的最大特征值为3，根据式（4），CI=0，判定该矩阵完全一致。最大特征值对应的特征向量为（0.4826，0.4826，0.1428）T，因此，三种工况的权重系数分别为0.4826、0.4826、0.1428，将其带入目标函数。刚度的权重系数w 取0.6，频率的权重系数则为0.4。

3.3 优化结果

经过多次迭代的优化结果，如图2 所示。吊挂体积缩减为原来的35%，结构整体呈左右对称性布置，载荷传力路径较为清晰。得到的拓扑优化模型同时满足多工况刚度最大和固有频率最大的要求。拓扑优化前后，飞机发动机吊挂不同工况下位移云图和应力云图，如图3～图8 所示。数据对比结果，如表6 所示。优化后模型的最大位移有所增加，但都小于最大允许位移20mm，各工况下最大应力明显增大，但均小于材料的屈服强度470MPa，拓扑优化结果满足设计要求。

表5 吊挂后安装架所受载荷Tab.5 Load of Pylon Rear Mounting Bracket

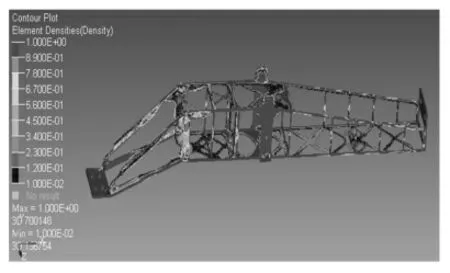
图2 飞机发动机吊挂拓扑结构Fig.2 Topology of Aircraft Engine Pylon

图3 优化前吊挂急着陆工况1 位移云图及应力云图Fig.3 Displacement and Stress Nebuligram of the Optimized Forehang Emergency Landing Condition 1

图4 优化后吊挂应急着陆工况1 位移云图及应力云图Fig.4 Displacement Nephogram and Stress Nephogram of Emergency Landing Condition 1 After Optimization

图5 优化前吊挂应急着陆工况2 位移云图及应力云图Fig.5 Displacement Nephogram and Stress Nephogram of Emergency Landing Condition 2 of Optimized Forehang

图6 优化后吊挂应急着陆工况2 位移云图及应力云图Fig.6 Displacement and Stress Nebuligram of Emergency Landing Condition 2 After Optimization

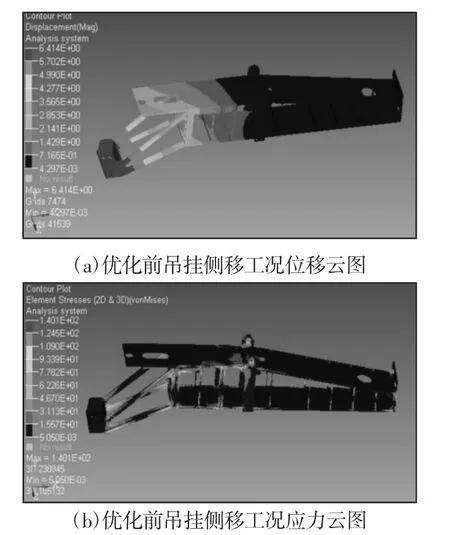
图7 优化前吊挂侧移工况位移云图及应力云图Fig.7 Displacement Nebulizer and Stress Nebulizer of Optimized Front Suspension Lateral Movement Condition

图8 优化后吊挂侧移工况位移云图及应力云图Fig.8 Displacement Nebuligram and Stress Nebuligram of the Suspension in the Optimized Lateral Movement Condition

表6 拓扑优化结果Tab.6 Results of Topology Optimization

柔度目标和频率目标的函数迭代曲线，如图9、图10 所示。各工况柔度目标迭代曲线由相同的波动趋势，整体呈下降趋势，而固有频率函数呈上升趋势，可以看出柔度和频率是相互制约的，迭代过程曲线虽有小幅度震荡，但吊挂的两种性能同时得到了提升。

图9 各工况柔度迭代曲线Fig.9 Compliance Iteration Curve for Each Condition

图10 频率优化迭代曲线Fig.10 Iteration Curve of Frequency Optimization

4 结论

（1）将采用折衷规划法对多目标函数模型进行拓扑优化的方法，应用于盒式梁式结构飞机发动机吊挂的轻量化设计，建立了多工况刚度和固有频率的综合目标函数，基于层次分析法，得到了吊挂各工况的权重系数，进一步完善了优化模型。

（2）在满足设计要求的前提下，多目标拓扑优化后的模型由原来的230.5kg 减小为80.7kg，各工况柔度均有明显下降，从3.0×105N.mm 左右减小到1.0×105N.mm 左右，增大了动态低阶频率，频率值从3.7×10-5Hz 增加到8.0×10-5Hz，传力路径更加合理，保证结构具有良好的动静态性能。结果表明采用折衷规划法对飞机发动机吊挂进行多目标拓扑优化是可行且有效的。