交流接触器动作值仿真计算

苏秀苹，田海波，付 哲，程浩峰

（1.河北工业大学电气工程学院省部共建电工装备可靠性与智能化国家重点实验室，天津300130；2.河北工业大学电气工程学院河北省电磁场与电器可靠性重点实验室，天津300130）

1 引言

交流接触器主要用于控制电机并和继电器或其它保护装置组合对电机进行保护，也可用于控制其它的电力负载[1]。设计一种新的交流接触器产品或者改进一项生产工艺，其方案是否可行，需要通过试验来验证[2-3]。交流接触器能否在电网电压下准确地吸合和释放需要通过动作值的测量测试来验证。由于电网电压的波动，有时电压低于交流接触器的额定电压，如果吸合电压过高，就会导致交流接触器的动静铁心吸合不上。另外，当接触器的线圈断电时，虽然电磁系统的励磁磁势和线圈电流都减小到零，然而，动铁心和静铁心中的磁感应强度不会减小到零，而是会沿着硅钢片的退磁曲线减小到固定值，因此电磁系统的气隙中存在剩余磁通，即剩磁现象[4-5]。当动静铁心吸合后，如果硅钢片的剩磁磁感应强度和矫顽力越大，铁心之间的气隙越小，则气隙中的剩余磁通就越大，如果由于剩余磁通所产生的电磁吸力大于动静铁心闭合位置的反力时，励磁线圈断电后动铁心和静铁心不能释放，这将导致严重的事故[6]。因此，交流接触器正常工作的首要条件就是其电磁系统能够可靠地吸合和释放，而不至于停留在中间。动作值的测量的目的是通过测量接触器的吸合电压和释放电压，来检验产品是否符合产品的技术指标要求或低压电器的产品标准规定，以保证接触器的正常工作。

利用电磁场仿真软件创建交流接触器电磁系统的吸合电压测试的有限元模型和释放电压测试的有限元模型。对接触器的吸合过程进行仿真，根据动静铁心间的气隙随时间的变化情况和动铁心的速度随时间的变化情况，判断动静铁心是否刚刚吸合，测量吸合电压值。对其释放过程进行仿真，根据动静铁心间的气隙随时间的变化情况和动铁心的速度随时间的变化情况，判断动静铁心是否刚刚释放到初始位置，测量释放电压值。再通过二分法在需要的精度范围内搜索接触器的准确吸合电压值和释放电压值，并利用公式进行换算得到标准规定的测试条件下的吸合电压值和释放电压值。

2 交流接触器的动作范围

根据标准中的要求，交流接触器准确无误吸合的电压范围为（85%～110%）UN（UN为励磁线圈电压）[7]，测试的条件是在环境温度上限（40℃）于热态时进行。热态是指被测试的电器在额定工作制下工作，然后将其线圈通以标准规定的电压发热至稳定温升的状态。对于研究的交流接触器来说，将励磁线圈通以额定工作电压，使其温升达到稳定值的状态。

交流接触器的能够完全释放的电压范围为20%UN～75%UN。测试的条件是在环境温度下限（-5℃）于冷态时进行。

3 电磁系统动态特性数学模型

电磁系统的功能是将线圈产生的电磁能转换为机构运动的机械能，并驱动动静触头和动静铁心的闭合和打开。为减小动静铁心产生的热量传递给线圈，电磁系统内部具有线圈骨架，在其上缠绕励磁线圈。励磁线圈通电后在线圈内部产生励磁电流进而在其周围形成一定强度的磁场，铁心被磁化后受到电磁吸力作用开始做机械运动。

电磁系统的动态特性由两部分组成，其中一部分是电磁吸力和反作用力对动铁心运动参数的影响；第二个是电磁参数对作用在动铁心上的电磁吸力的影响[8]。这两个问题相互联系且相互影响。可由电压平衡方程和达朗贝尔运动方程表示，电磁系统动态过程状态方程组[9]，如式（1）所示：

式中：Ψ（t）—通过电磁系统的磁链（Wb）；u、i—电路中的电压值（V）和电流值（A）；Fx—电磁系统中的电磁吸力（N）；Ff—动铁心受到的反力（N）；x—动铁心在任一时刻的位移（m）；v—动铁心在任一时刻的速度（m/s）。

4 电磁场理论及电磁系统有限元模型的建立

4.1 三维瞬态磁场计算原理

麦克斯韦方程在低频瞬态磁场的情况下可以写成式（2）的形式[10]。

式中：H—磁场强度（A/m）；E—电场强度（V/m）；B—磁通密度（T）。

通过式（2）得出两个恒等式，如式（3）所示。

式中：σ—电导率（S/m）。

以电压源作为励磁线圈中的激励源，采用绞线型的线圈绕组，其电阻值是已知的。对于动铁心的吸合过程和释放过程，需要对位移进行离散计算，离散的格式[11]，如式（4）所示。

式中：x—动铁心的位移量。

4.2 电磁系统有限元模型的建立

分析电磁系统的瞬态电磁特性是通过软件中的三维瞬态磁场模块进行的，其有限元模型的创建包括各种实体建模、材料的定义、网格的划分、添加交流电压源激励、设置动铁心的运动属性等。

在瞬态磁场中，必须要建立动铁心的运动求解域（即band域）。因为在软件中的三维瞬态磁场模块添加运动求解域时，必须采用具有真实边界的三维实体（即圆柱体域不能作为band 域），因此根据动铁心的结构型式设定与其相同形状的band 域，且动铁心中间的圆柱形孔应简化为多边形柱体。band 应包围动铁心及其运动区域，同时不能与静止的物体如线圈、静铁心、分磁环等相交。建立的电磁系统模型，如图1 所示。

在材料的定义中，将动静铁心定义为硅钢片材料，线圈设定为铜，且为绞线型线圈，在环形截面上施加交流电压源激励源。设定求解区域和band 域为真空材料。由于励磁线圈中的电流是交变的，组成动静铁心以及分磁环的材料的磁导率较高，交变电流产生的交变磁通会在其内产生闭合回路，交变的磁通在铁磁体内产生磁滞和涡流损耗。因此在对电磁系统中的某些部件进行剖分时要考虑集肤效应，故采用对物体边界（On Selection）进行剖分，剖分时要计算集肤效应的透入深度，计算公式，如式（5）所示。

式中：b—透入深度（m）；ρ—导体的电阻率（Ω·m）；μ—导体材料的磁导率（H/m）；f—电流的频率（Hz）。

其余的部分采用对物体内部（Inside Selection）进行剖分。

图1 电磁系统模型Fig.1 Model of Electromagnetic System

4.3 反力的设置

动铁心受到反力包括反力弹簧的反力和触头的反力，其运动形式是上下直线运动，设定向上运动为正方向。对反力弹簧、触头弹簧的初压力和终压力以及动铁心运动情况进行分析，得出反作用力公式为：

式中：Ff—动铁心受到的反力（N）；δ—动静铁心间的气隙（mm）。

反力特性图，如图2 所示。

图2 反力特性Fig.2 Characteristic of Reaction Force

通过if 函数在软件的运动属性设置中设定动铁心受到的反力。对求解器进行设定，设置求解的时间、步长，最后从仿真结果可以得到动静铁心间的气隙随时间的变化情况以及动铁心的速度随时间的变化情况，从中可以得到动静铁心是否刚刚吸合和刚刚释放。

5 仿真方法

5.1 吸合电压测定的仿真

通过软件对接触器的吸合过程进行分析，寻找动静铁心刚刚吸合时的电压，来进行的吸合电压的测量。吸合电压的测量需要在环境温度上限的情况下的热状态时进行，而在模拟测试中不满足环境温度上限的条件，可以通过串联附加电阻的方法来解决。将线圈处于热态时的电阻与附加电阻串联连接，该附加的电阻阻值相当于周围环境温度增加而引起线圈电阻增加的阻值，也就是计入了环境温度的上限值。在仿真时就是将电阻值一同计入线圈电阻里。其中，线圈的热态电阻是已知的，为142.5Ω。

附加电阻为：

式中：θ1—常温时周围空气的温度，为25℃；R1—在常温和冷态下测量线圈的电阻值，为122.2Ω；θ2—环境温度上限，为40℃；α—导体的电阻温度系数，对于铜，α=1/234.5。

为模拟在电网电压下励磁线圈电压合闸相角的随机性，通过计算机编程随机产生合闸相角值作为每次电压的合闸相角值。首先将线圈电压调到预期动作值即85%UN，验证其是否能够可靠吸合。然后逐渐降低线圈电压值，再进行瞬时接通电路进行仿真，直到某次仿真试验的电压值下动静铁心不能吸合，记下此时的线圈电压值和上次动静铁心吸合时的电压值，以这两个值为初始值进行二分法来查找交流接触器的吸合电压值。通过仿真得出当线圈电压值为85%UN时动静铁心能够可靠地吸合，从而满足了国家标准的要求。通过仿真结果得出动静铁心不能吸合时的线圈电压值为50%UN，上次试验吸合时的线圈电压值为60%UN。即取50%UN和60%UN作为初始值进行二分法。令a=50%UN，b=60%UN，取x0=（50%+60%）UN/2=55%UN，测试得到动静铁心吸合，则令a1=50%UN，b1=55%UN，重复这样的过程，可以得到一系列的电压范围［a，b］⊃［a1，b1］⊃［a2，b2］⊃…⊃［ak，bk］⊃…，每个区间都是前一个区间的一半，当k→∞时［ak，bk］的长度为bk-ak=（b-a）/2k趋于零，即最后的小区间会收缩于一点x*[12]。x*就是测得的吸合电压值。

数值分析的结果允许带有一定的误差，由于：

图3 吸合电压测定流程图Fig.3 Flow Chartfor Measurement of Pull-in Voltage

测试结果，如表1 所示。表中如果动静铁心吸合时，测试值后面标（＋），否则标（－）。表中，xk=（ak+bk）/2。

表1 测试结果Tab.1 Test Result

又因为在产品的型式试验中，交流接触器的吸合电压试验次数不少于20 次，所以在线圈电压为52.19%UN时，通过计算机程序随机产生25 个合闸相角值，又进行25 次试验仿真，在这25次试验中接触器均能吸合，因此测定的吸合电压值为52.19%UN。满足低压电器产品标准的要求：热态的吸合电压不超过85%UN。

环境温度上限情况下于热态时，励磁线圈电压为52.19%UN，动静铁心间的气隙和动铁心的速度随时间的变化曲线，如图4 所示。

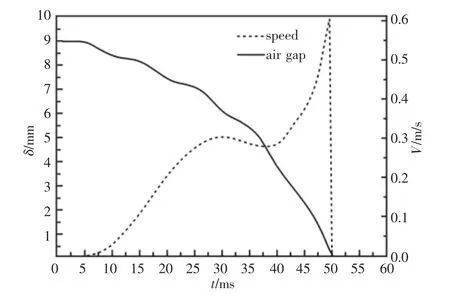
图4 气隙和速度随时间的变化Fig.4 Curves of Air Gap and Speed

从图4 中可以看出，动静铁心在时间t=50ms 时能够刚刚吸合，此时动铁心的速度也降为零，吸合速度V=0.6m/s。

环境温度上限情况下于热态时，线圈所通电压为52.19%UN时，吸反力特性曲线，如图5 所示。

图5 吸反力特性曲线Fig.5 Curves of Suction and Reaction

由图5 可以看出，在面积S1（吸力和反力特性曲线所围成的局部区域）内，F>Ff。在S2内，FS4，S5>S6，S7>S8，S9>S10，S11>0。因此动铁心的剩余动能总是大于零，能够在吸合过程中不停滞在中间，吸合到底。由上面分析知，在吸动值时，每次式（9）等于一个足够小的正数时，即：

则吸合时的速度v>0。

式中：S2i-1—F>Ff期间的动能的存储量；S2i—F

从图5 中可以看出，吸反力配合较好，动铁心的剩余动能较小，可以使动静铁心刚好吸合。此时的励磁线圈两端的电压即为接触器的吸合电压。

5.2 释放电压测定的仿真

对于释放电压的仿真测量，是通过连续地将励磁线圈电压值从额定值降低，一直降到动静铁心刚刚打开时为止，此时的线圈电压值即为交流接触器的释放电压值。释放电压的测定条件是线圈处于冷态时于环境温度下限时进行，但模拟测试条件不满足环境温度的下限，因此先在常温下于冷态时测定释放电压值。然后，通过公式转换的方法得到标准试验条件下的释放电压值。

仿真方法是：首先将线圈电压从额定值起连续降低，一直降低到动静铁心释放为止，记录此时的线圈电压值和上次仿真试验动静铁心不释放的电压值，以这两个值为初始值进行二分法来查找动静铁心刚刚释放时的电压值即为交流接触器的释放电压值。通过仿真测试得出当线圈电压降到30%UN时动静铁心释放，上次试验的线圈电压为40%UN时动静铁心不释放。因此，以这两个值为初始值，进行二分法来查找释放电压值。测试要求结果精确到小数点后的第二位，按照误差估计式则由式得出要二分4 次达到预定的精度。

测试结果，如表2 所示。表中如果动静铁心释放，测试值后面标（＋），否则标（－）。表中，xk=（ak+bk）/2。

表2 测试结果Tab.2 Test Result

从表2 中的二分结果看出，常温下于冷态时的释放电压为39.06%UN，从软件仿真结果中得到常温下于冷态时的释放电流值I1为0.331A。再通过转换公式得到线圈电阻冷态时环境温度下限时的释放电压值。

式中：U0—环境温度下限于冷态时的释放电压值；U1—常温下于冷态时的释放电压值；I1—常温下于冷态时的释放电流值；R1—常温及冷态下测量线圈的电阻值，为122.2Ω；R0—环境温度下限于冷态时的线圈电阻值。

R0的计算公式为：

式中：θ1—常温下周围空气的温度，为25℃；θ0—环境温度下限，为-5℃；α—导体的电阻温度系数，对于铜，α=1/234.5。

通计算得到U0=83.90V=38.14%UN。满足了标准要求：交流接触器的释放电压的范围为（20%～75%）UN。

在常温下于冷态时线圈电压为39.06%UN时，动静铁心间的气隙和动铁心的速度随时间变化的曲线图，如图6 所示。

图6 气隙和速度随时间的变化Fig.6 Curves of Air Gap and Speed

从图中可以看出当t=30ms 时动静铁心能够刚刚释放到初始位置，而此时动铁心的速度也减小到零，释放速度V=0.55m/s。

将常温下于冷态时线圈电压为39.06%UN的吸反力特性曲线画出，如图7 所示。

对于图7 的分析和吸合电压测量时的吸反力特性分析相似，从图中可以看出，S1>S2，S3>S4，S5>S6，S7>S8，S9>S10，动铁心的剩余能量一直在减小，能够使得动静铁心刚好释放。此时的励磁线圈两端的电压值即为接触器的释放电压值。

图7 吸反力特性曲线Fig.7 Curves of Suction and Reaction

6 结论

（1）分析了交流接触器电磁系统的运动特性，建立测试吸合电压和释放电压的有限元模型，完整地模拟了实际动作特性试验。通过仿真和计算的方法测量动静铁心刚刚吸合和刚刚释放的电压值，利用二分法在需要的精度范围内搜索接触器的准确吸合电压值和释放电压值，提高了仿真的精确度。

（2）通过吸合电压下和释放电压下的动静铁心间气隙随时间的变化曲线以及动铁心运动速度随时间的变化曲线来验证吸合电压值和释放电压值。从变化曲线图中可以得出动静铁心刚刚吸合时，动静铁心之间的气隙变为零，同时动铁心的速度也下降为零，动铁心刚刚释放到初始位置时，动铁心的速度也下降为零，从而验证了仿真结果的正确性。

（3）通过以上的仿真和计算，得出交流接触器的吸合电压值为52.19%UN，释放电压值为38.14%UN。此仿真计算方法能够在标准试验条件不满足的情况下准确地测试和计算接触器的动作值，为接触器的动作试验提供了思路。