全矢谱在滑动轴承转子系统裂纹中的应用

周玉平，高 山，陈 磊，马凌云

（郑州大学机械工程学院振动工程研究所，河南 郑州 450001）

1 引言

轴承作为机械设备中最常见、最易损坏的器件之一其运行状态直接影响机械设备的寿命[1]。文献[2]通过ANSYS 仿真软件研究了含基座的滑动轴承转子裂纹系统故障诊断方法。文献[3]采用应变能释放率法计算裂纹单元刚度矩阵，并引入到裂纹转子系统整体有限元模型中，基于时域、频域和在线识别方法对裂纹转子故障诊断做了研究。文献[4]提出基于全矢Hilbert 解调方法和全矢HHT 时域边际谱方法，通过理论阐述和仿真验证了其有效性。

将全矢谱应用到滑动轴承转子系统故障诊断中，在ANSYS中建立滑动轴承双盘转子-滑动轴承系统有限元模型[5]，运用全矢谱得到裂纹故障的全矢HHT 时域边际谱，表明该信号能更好的识别该系统裂纹的故障特征。实例验证，全矢HHT 时域边际谱在该转子系统裂纹故障诊断中的完整性。

2 全矢HHT 时域边际谱原理

2.1 全矢谱技术

设｛xn｝，｛yn｝分别是x，y 方向上的离散序列，其构成复序列｛zn｝=｛xn｝+j｛yn｝（n=1，2，…，N/2-1）其中j 为虚数，进一步提高了计算效率。通过傅立叶变换可以得到｛Zn｝=｛ZRn｝+j｛Zin｝，其中｛ZRn｝和｛Zin｝是｛Zn｝的实部和虚部。由此可快速计算得出：（具体推导过程参见文献[6-7]）：

式中：椭圆长轴Ran—主振矢，短轴Rbn—副振矢；αn—主振矢与x

轴夹角；φn—初始相位角。

2.2 HHT 变换原理

Hilbert-Huang 变换[8-9]是一种处理非平稳信号的时频分析方法，包括经验模态分解（EMD）及Hilbert 变换两部分，假设任何信号x（t），对其进行EMD 分解，得到各个通道的固有模态函数（IMF），对其进行Hilbert 变换求得瞬时频率。

对每个IMF 作Hilbert 变换：

式中：p—柯西主分量。

通过这个变换，xi（t）和yi（t）可以组成解析信号定义瞬时频率为则：

这里忽略了残余项，因为它不过是单调函数或常数值。展开式称为Hilbert 幅值谱，简称Hilbert 谱，记作：

进一步可定义边际谱：

以上EMD 和与之相的Hilbert 谱信号分析方法统称为Hilbert-Huang 变换，简称HHT。h（ω）为Hilbert 谱H（ω，t）对时间的积分，它反映了整个频率段上信号幅值随频率的变化情况，能够准确地反映信号的实际频率成分。某一（瞬时）频率的边际谱的幅值反映了该频率的总能量，是该（瞬时）频率所有时刻的能量的总和[10]。

3 系统仿真

3.1 滑动轴承转子系统仿真模型建立

用ANSYS 建立滑动轴承双盘转子系统，SOLID186 单元用来模拟裂纹，但若整个模型全部采用SOLID186 单元，则会大大增加节点数量，模型计算量大大增加，不利于计算，因此，将整个模型进行划分，裂纹轴端用实体单元SOLID186 进行模拟，其余轴端用BEAM188 进行模拟，同时用MASS21 单元模拟两个转盘，用COMBI214 弹簧单元模拟两个轴承，转子系统质量只考虑两个转盘的质量，且不考虑转轴的变形。裂纹宽H1=1mm，深度H3=5mm，滑动轴承双盘转子裂纹模型，如图1 所示。滑动轴承转子系统参数，如表1 所示。

图1 滑动轴承双盘转子裂纹模型Fig.1 Brief Diagram of Crack Model of Double Disc Rotor of Sliding Bearing

表1 滑动轴承双盘转子系统参数Tab.1 Parameters of Double Disk Sliding Bearing Rotor System

3.2 固有频率及临界转速计算

约束模型Z 方向平动位移和转动位移，并约束模型X、Y 方向转动位移，约束机架所有位移。考虑陀螺效应，设置CORIOLIS为ON。设置分析类型为模态分析，采用DAMP 阻尼法，提取16阶模态。求出多个自转频率值所对应的进动频率值，设置转子的转速分别为0r/min，2000r/min，5000r/min，8000r/min，9000r/min，10000r/min，11000r/min。经模态分析后，系统坎贝尔图，如图2 所示。FW 为正向涡动，BW 为反向涡动。

图2 滑动轴承双盘转子系统坎贝尔图Fig.2 Campbell of Double Disk Sliding Bearing Rotor System

图中1X 激振曲线和一阶、二阶固有频率的交点为系统一阶、二阶临界转速，经计算，一阶、二阶临界转速分别为742.245rad/s 和1073.4rad/s。系统在一阶临界转速下平稳运行，因此选取系统转速为400rad/s 的工况下进行分析。

3.3 模型可行性验证

为证实此模型的正确性，将无裂纹时耦合之后的模型与不采用实体单元SOLID186 的模型进行对比，分别计算两个模型在400rad/s 系统转速时的固有频率，采用ANSYS 模态分析阻尼法，提取前10 阶模态振型，经计算，两种模型所计算的系统前三阶固有频率，如表2 所示。两种模型的转子系统前三阶固有频率基本相同，因此可使用该模型进行分析。

表2 转子系统两种模型固有频率表Tab.2 Natural Frequency Table of Two Models of Rotor System

在裂纹轴端上插入宽1mm，深度为3mm 的裂纹，实体单元采用自由网格划分，梁单元采用线网格划分，并细化裂纹处的网格，计算滑动轴承裂纹双盘转子系统的前三阶固有频率，与无裂纹时的前三阶固有频率对比结果，如表3 所示。可知有裂纹时滑动轴承转子系统的固有频率降低，这与理论值相符。

表3 无裂纹时和有裂纹时的系统固有频率对比表Tab.3 Comparison Table of Natural Frequency of System without Cracks and Cracks

3.4 全矢HHT 解调技术在裂纹故障中的应用

用ANSYS 瞬态分析即时间历程分析来模拟转子转动过程，并采用完全法瞬态分析。设置OMIGAZ 为400rad/s，计算子步数为5120 步，取（0.2～0.5）s 之间的数据，即采样点数为816，相零两点间时间间隔为3.9e-4s，即模拟采样频率为2560Hz。转盘1 中心X 方向和Y 方向位移随时间变化的时域图，如图3 所示。对转盘1 中心X、Y 方向的信号进行EMD 分解，分别将其IMF 分量进行Hilbert 变换，得到HHT 时域边际谱，再分别对单通道的HHT时域边际谱进行FFT 变换，得到其HHT 时域边际谱频谱图，如图4 所示。

图3 单通道信号时域图Fig.3 Single-Channel Signal Time Domain Diagram

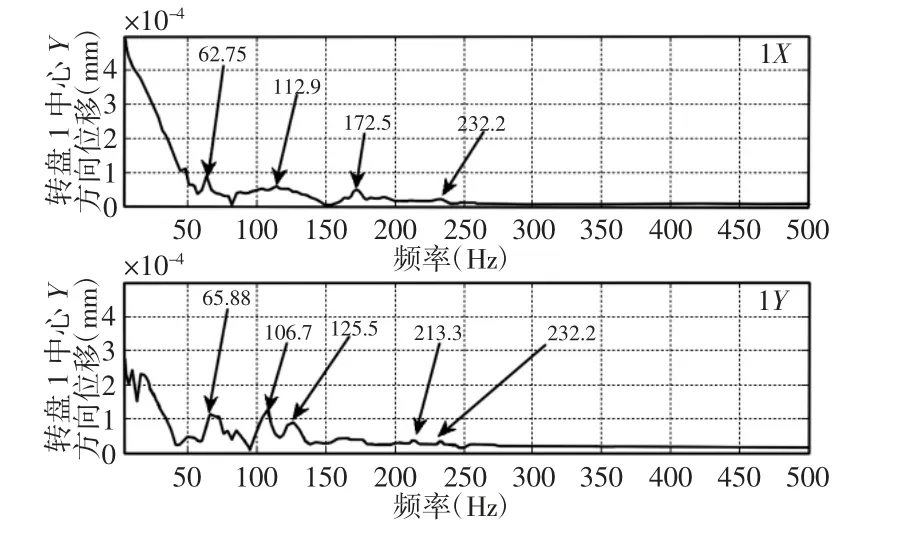
图4 通道信号HHT 时域边际谱频谱Fig.4 HHT Time-Domain Marginal Spectrum Spectrum for Single-Channel Signals

由图4 所示，HHT 时域边际谱频谱能够大致反映系统的振动特性，但是，仅看X 通道信号特征，其特征频率不是很明显，容易被忽略，且X 通道中没有125.5Hz 特征频率。Y 通道中没有172.5Hz 特征频率。因此，仅凭单通道的信号特征进行故障分析，具有局限性，进而对故障诊断结果造成误判。

将全矢谱技术与HHT 时域边际谱技术相结合，得全矢HHT时域边际谱，如图5 所示。全矢HHT 时域边际谱反映了x、y 通道频谱信号的特征信息，其比X 通道信号的特征信号更为突出，其比Y 通道信号的特征频率更为纯粹，能更好的识别裂纹故障。该技术为转子系统发生裂纹故障时的诊断提供了一种新的诊断方法。由全矢HHT 时域边际谱得，当转子系统发生裂纹故障时，除转频外，存在1.5X、2X、3X、4X 多倍转频，且伴随低倍频存在。

图5 全矢HHT 时域边际谱Fig.5 Full-Vector HHT Time Domain Marginal Spectrum

4 实例分析

在某大学振动研究所滑动轴承转子实验台上进行滑动轴承转子系统裂纹故障诊断实验，两组位移传感器分别安装在轴承座横截面互相垂直的两个方向上，实验工作转速为3600r/min，如图6（a）所示。使用郑州恩普特设备诊断工程有限公司生产的PDES-E 仪器进行同源信息采集，采样频率为7680Hz，采样长度为4096，如图6（b）所示。

图6 滑动轴承转子系统裂纹实验Fig.6 Crack Experiment of Rotor System of Sliding Bearing

选取滑动轴承转子系统裂纹信号中间段，即3096 个采样点，X 通道和Y 通道时域波形图，如图7 所示。

图7 单通道时域波形图Fig.7 Single Channel Time Domain Waveform

基于HHT 的时域边际谱是对单通道振动信号做EMD 分解，然后对其IMF 分量进行Hilbert 变换，得到HHT 时域边际谱，如图8 所示。对其做FFT 变换得到X 通道和Y 通道的单通道HHT 时域边际谱频谱，如图9 所示。由图8 和图9 可以看出，系统故障信号已经有比较明显的特征频率，说明HHT 时域边际谱在处理系统故障特征信号中有比较有效的作用。然而，对比X 通道信号和Y 通道信号的HHT 时域边际谱和其频谱，可以发现两个单通道的HHT 时域边际谱有所不同，Y 通道频谱中没有显示99.22Hz 特征频率、148.8Hz 特征频率和200.9Hz 特征频率，而X通道频谱中没有显示74.42Hz 特征频率，说明单通道的信息具有不完整性，仅凭单通道信息判断发生的故障类型，具有局限性。

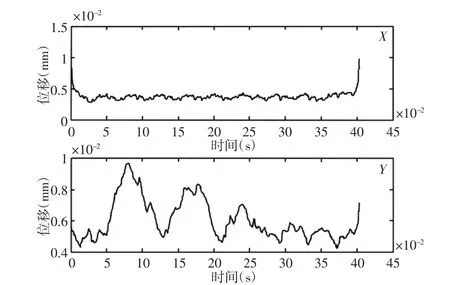
图8 单通道HHT 时域边际谱Fig.8 Single Channel HHT Time Domain Marginal Spectrum

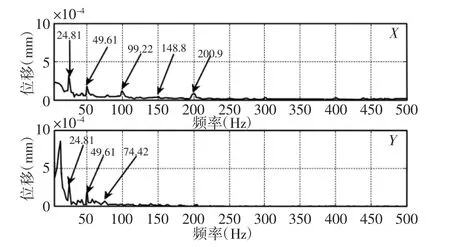
图9 单通道HHT 时域边际谱频谱Fig.9 Single-Channel HHT Time-Domain Marginal Spectrum

融合了X、Y 通道同源信息后的全矢HHT 时域边际谱，如图10 所示。对比图9、10，全矢HHT 时域边际谱特征频率的幅值相对于单通道HHT 时域边际谱特征频率幅值有所增加，这有助于现实中读取裂纹特征频率信号。同时，全矢HHT 时域边际谱显示了121.6Hz 特征频率，这在X 通道和Y 通道单通道HHT 时域边际谱中均没有显示。事实证明，经全矢谱技术融合后的全矢HHT时域边际谱更能反映滑动轴承转子系统裂纹故障诊断特征信号，这为滑动轴承转子系统裂纹故障诊断提供了一种新的方法。由全矢HHT 时域边际谱得，当滑动轴承转子系统产生裂纹时，系统伴随基频会出现转频的1.5X、2X、3X 高频特征频率，并且此时伴随低倍频存在，同时，由于滑动轴承交叉系数存在，在一定转速下，系统仍旧存在1/2X 转频。

图10 全矢HHT 时域边际谱Fig.10 Full-Scale HHT Time Domain Marginal Spectrum

5 结论

在滑动轴承双盘转子系统模型上建立裂纹，采用梁单元与实体单元耦合的方法建立滑动轴承双盘转子-滑动轴承裂纹转子系统，通过ANSYS 完全瞬态分析方法得到转子系统同一截面上互相垂直的两组同源信号，并得到其HHT 时域边际谱；基于全矢谱技术融合两组同源信号得到全矢HHT 时域边际谱，结合实验分析，说明全矢HHT 时域边际谱能更好的应用于滑动轴承裂纹转子系统故障诊断分析中，这为滑动轴承裂纹转子系统的故障诊断提供了一中新的方法。全矢HHT 时域边际谱显示，当滑动轴承转子系统发生裂纹故障时，系统存在1.5X、2X、3X、4X 多倍转频，并且此时伴随低倍频存在。