三节点单拉杆式轴箱定位刚度研究
张 江, 刘高坤, 刘启昂
(1 克诺尔车辆设备(苏州)有限公司, 江苏苏州 215011;2 中铁第四勘察设计院, 湖北武汉 430063;3 西南交通大学 牵引动力国家重点实验室, 四川成都 610031)
三节点单拉杆式轴箱定位刚度研究
张江1, 刘高坤2, 刘启昂3
(1克诺尔车辆设备(苏州)有限公司, 江苏苏州 215011;2中铁第四勘察设计院, 湖北武汉 430063;3西南交通大学牵引动力国家重点实验室, 四川成都 610031)
推导了三节点单拉杆式轴箱定位刚度的理论计算公式,然后利用SIMPACK建立了三节点单拉杆的物理模型,通过该模型验证了理论公式的正确性,同时探讨了拉杆等效刚度的影响因素。结果表明:三节点单拉杆等效刚度的理论计算公式能够反映实际情况,拉杆的横向、纵向和垂向等效刚度误差均在10%范围内;拉杆纵向长度对拉杆的横向和垂向等效刚度影响明显,当长度增加时,横向和垂向等效刚度显著减小;拉杆不对称因素对拉杆的横向、垂向等效刚度无影响,而对拉杆纵向等效刚度影响明显,且随着不对称因素的增加,拉杆纵向等效刚度先增大后减小,最后趋于平稳;拉杆的横向等效刚度随着拉杆横向长度的增加而近似呈线性增加。
三节点单拉杆; 轴箱定位刚度; 拉杆等效刚度
三节点单拉杆(以下简称拉杆)轴箱定位结构如图1,通过拉杆两端3个橡胶关节连接轴箱与构架,通常两个关节与构架安装座连接,另一端关节与轴箱体连接。三节点拉杆轴箱定位结构较为紧凑,可在有限的结构空间内实现较大的轴箱横向定位刚度。轴箱垂向定位刚度主要由一系弹簧提供,轴箱横向和纵向定位刚度主要由拉杆的橡胶关节提供。三节点拉杆式轴箱定位可实现较大的横向刚度和一系悬挂垂向静挠度,对机车车辆来讲增大转向架一系弹簧的柔度有利于降低轮轨垂向力。
根据轴箱弹簧布置型式可分为两类:一系弹簧对置(主要用于机车)和一系弹簧顶置(主要用于地铁车辆)。
目前,我国铁道机车车辆中采用三节点单拉杆式轴箱定位方式的主要是CRH5[1],通过对该种定位方式的定位刚度的研究为我国铁路机车车辆转向架一系定位设计计算提供参考。

图1 三节点单拉杆轴箱结构图
1 拉杆等效刚度计算
针对一般的拉杆进行刚度分析,假设拉杆的三边的长度不同,且三个节点的刚度也不同,拉杆的几何参数如图2所示。节点A与轴箱连结,节点B、C与转向架构架相连。关节参考坐标采用统一的铁路坐标系表示,如图2,拉杆相关参数及符号如表1所示。
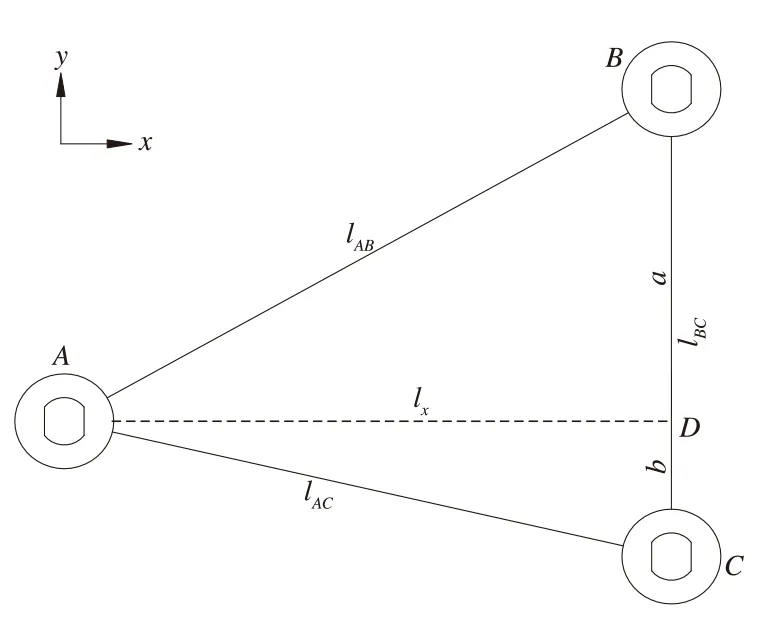
图2 拉杆几何参数
1.1拉杆纵向等效刚度kx
当拉杆的∠ACB或∠ABC不为钝角时,拉杆节点A的芯轴在纵向力P作用下的变形和受力如图3。
拉杆A端芯轴在力P作用下相对拉杆的纵向位移为Δx1,由拉杆转动产生的附加位移为Δx2,拉杆B端相对B芯轴的纵向位移为ΔBx,拉杆C端相对C芯轴的纵向位移为ΔCx,拉杆D端相对构架的纵向位移为ΔDx。则A端关节芯轴相对于转向架构架的纵向位移为Δx=Δx1+Δx2,在小变形情况下,Δx2≈ΔDx,φ为拉杆转动的角度。

表1 拉杆节点参数符号
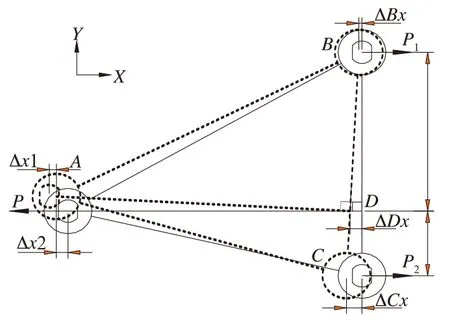
图3 拉杆纵向受力和变形图
根据拉杆的受力与几何关系可得如下关系式:
(1)
由方程组(1)解得拉杆的纵向等效刚度:
(2)
当拉杆的∠ACB或∠ABC为钝角时,拉杆节点A的芯轴在纵向力P作用下变形和受力如图4,这里忽略节点偏转刚度对拉杆纵向等效刚度的影响。
A端芯轴在力P的作用下相对拉杆的位移为Δx1,拉杆在力P的作用下,拉杆B端相对B芯轴的纵向位移为ΔBx,拉杆C端相对C芯轴的纵向位移为ΔCx,则拉杆上虚拟点D相对构架的纵向位移为ΔDx,A端关节芯轴相对于转向架构架的纵向位移为Δx=Δx1+Δx2,在小变形情况下,Δx2≈ΔDx,r1为B点到转心O的距离,r2为C点到转心O的距离,φ为拉杆转动的角度。
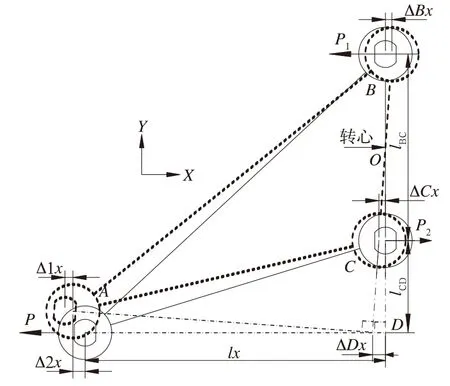
图4 拉杆纵向受力和变形图
根据拉杆的受力与几何关系可得如下关系式:
(3)
由方程组(3)解得拉杆的纵向等效刚度:
(4)
为简化纵向等效刚度计算结果,将上述两种情况进行数学统一,得到拉杆的纵向等效刚度kx,忽略节点回转刚度(由2.1的仿真研究表明,忽略节点回转刚度对计算结果的误差小于1%),可得:
(5)
其中:lBC=a+b,lBD=a,lCD=b,当三节点拉杆的∠ACB或∠ABC为钝角时,b的取值为负。
1.2拉杆横向等效刚度ky
拉杆A端芯轴在横向力P的作用下的变形和受力分别如图5和图6。

图5 拉杆横向变形图
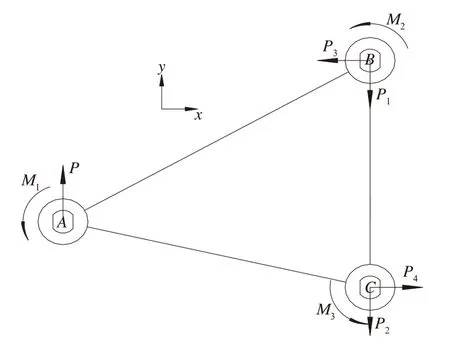
图6 拉杆横向受力图
如图,拉杆在横向力P作用下,A端芯轴相对构架的横向位移Δy可看成A端芯轴相对拉杆的横向位移Δy1,拉杆相对构架的横向位移Δy2,和拉杆A点由拉杆回转运动产生的附加横向位移Δy33部分组成。设拉杆绕力平衡回转中心O旋转的角度为ψ,则Δy3=ψ·r1,由于转动角 较小,r1≈lx。
由拉杆的力平衡和变形协调可得:
由方程组(6)解得拉杆的横向等效刚度:
(7)
1.3拉杆垂向等效刚度kz
拉杆A端芯轴在垂向力P的作用下的变形和受力如图7。
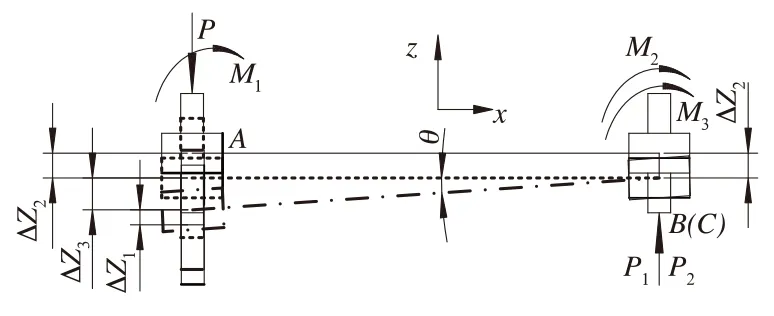
图7 拉杆垂向受力及变形图
拉杆A端芯轴相对构架的垂向位移Δz可看成A端芯轴相对拉杆的垂向位移Δz1,拉杆相对构架的垂向位移Δz2和拉杆A点因拉杆绕y轴的回转运动而产生的附加垂向位移Δz33部分之和。设拉杆的回转角为θ,则Δz3=lxθ,由拉杆的力平衡和变形协调可得:
(8)
由方程组(8)解得拉杆的垂向等效刚度
(9)
1.4三节点拉杆式轴箱定位刚度
轴箱定位刚度可看成拉杆的等效刚度与一系簧刚度并联,因此可得轴箱的三向定位刚度计算公式。
(10)
2 拉杆等效刚度公式验证
利用SIMPACK软件[2]建立拉杆的计算模型,如图8,由于与构架相连的两个芯轴通过螺栓与构架刚性连接,因此这两个芯轴不用单独建模,这样模型由拉杆以及与轴箱端连接的芯轴两个刚体组成。拉杆具有6个自由度,芯轴只具有三向平动自由度,芯轴与拉杆之间用6自由度的力元相连接以模拟橡胶节点的各向刚度,与构架连接的两个节点同样用6自由度的力元来模拟。
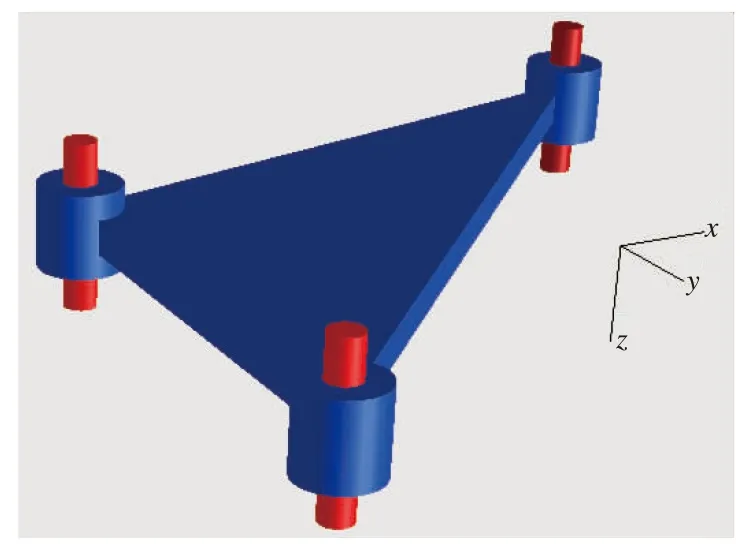
图8 拉杆的力学模型
2.1理论计算与仿真结果比较
通过在芯轴上分别施加x、y、z向的外力得到芯轴对应的x、y、z向位移,从而得到拉杆x、y、z向的等效刚度。同时为了验证不同结构尺寸拉杆的等效刚度计算公式,采用表2的6组拉杆参数来计算相应的拉杆等效刚度。
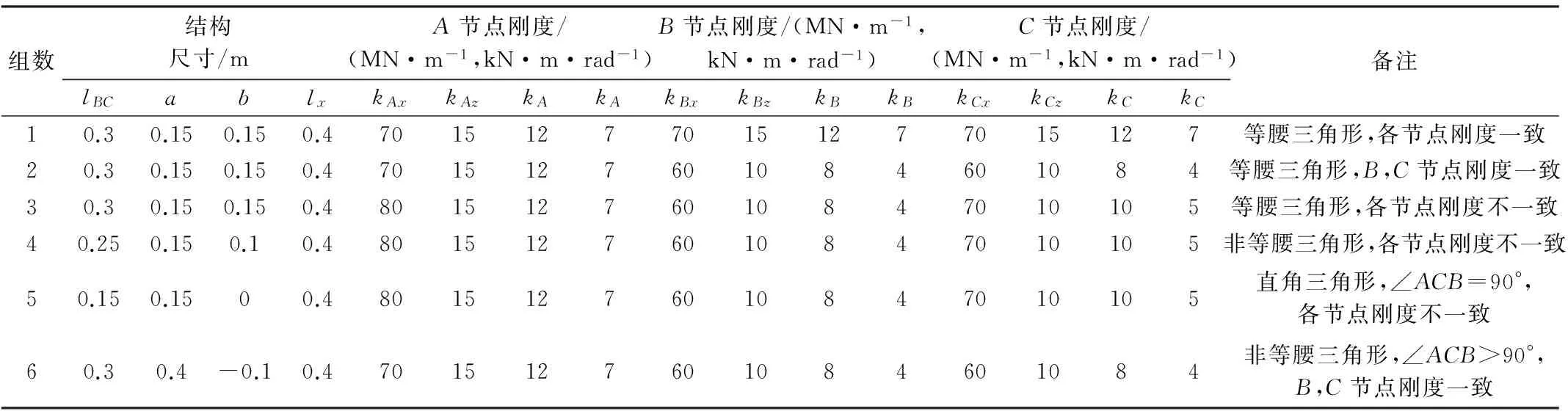
表2 拉杆计算参数
将仿真计算结果与理论公式(5),式(7),式(9)计算结果进行比较,得到仿真值与理论值的误差百分比,进而可以验证理论公式的正确性,如表3所示。
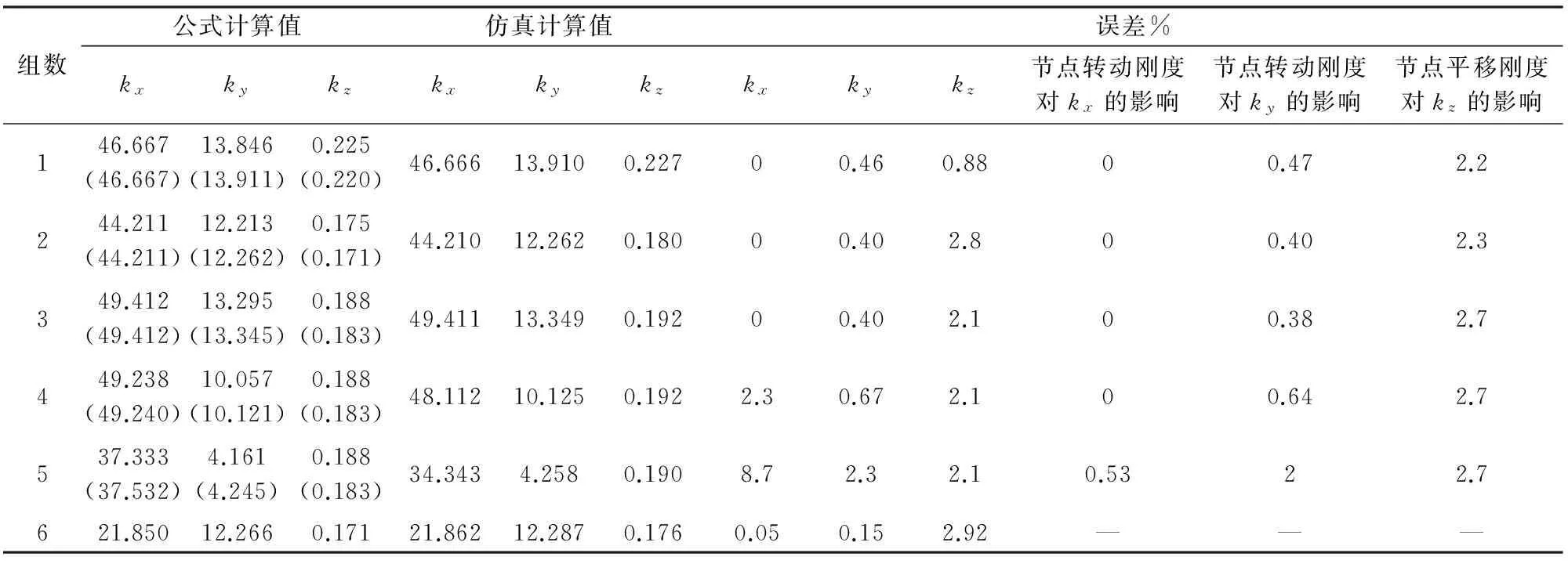
表3 公式计算值与仿真计算值对比
注:上述公式计算结果中,纵向刚度kx一栏,括号内为考虑节点绕z轴回转刚度的计算值;横向刚度ky一栏,括号内为考虑到节点绕z轴回转刚度的计算值;垂向刚度kz一栏,括号内为考虑节点沿z轴的垂向刚度的计算值,计算的误差百分比以非括号数据为准。
通过对表3中的数据进行分析,可得如下结论:
(1)拉杆的纵向等效刚度公式计算值与仿真值基本一致,当栏杆形状为直角三角形时误差较大,其他情况下误差非常小;拉杆的纵向等效刚度受到拉杆的结构尺寸影响明显,公式可以反映出拉杆结构尺寸的影响;节点的回转刚度对拉杆纵向等效刚度影响非常小,误差小于1%,可以将其忽略。
(2)拉杆的横向等效刚度公式计算值与仿真值基本一致,误差在3%以内;节点转动刚度对拉杆的横向等效刚度影响小于2%,可以将其忽略。
(3)拉杆的垂向等效刚度公式计算值与仿真值误差小于3%,拉杆节点的垂向平移刚度对拉杆垂向等效刚度的影响小于3%,可以将其忽略;拉杆的形状对拉杆垂向等效刚度没有影响。
由上可将三节点拉杆的等效刚度计算理论公式进一步简化为式(11)~式(13)。
拉杆纵向等效刚度kx(当∠ACB或∠ABC为钝角时,b的取值为负数)
(11)
拉杆横向等效刚度ky:
(12)
拉杆垂向等效刚度kz:
(13)
2.2拉杆几何参数对其等效刚度的影响分析
该节主要研究以下3个方面,拉杆的计算参数取表2中第2组数据。
拉杆长度lx对拉杆横向和垂向等效刚度的影响如图9、图10所示。
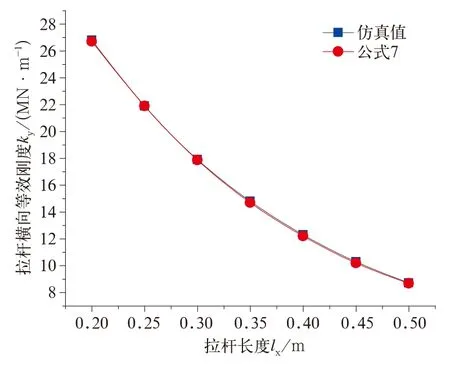
图9 拉杆长度lx对拉杆横向等效刚度的影响
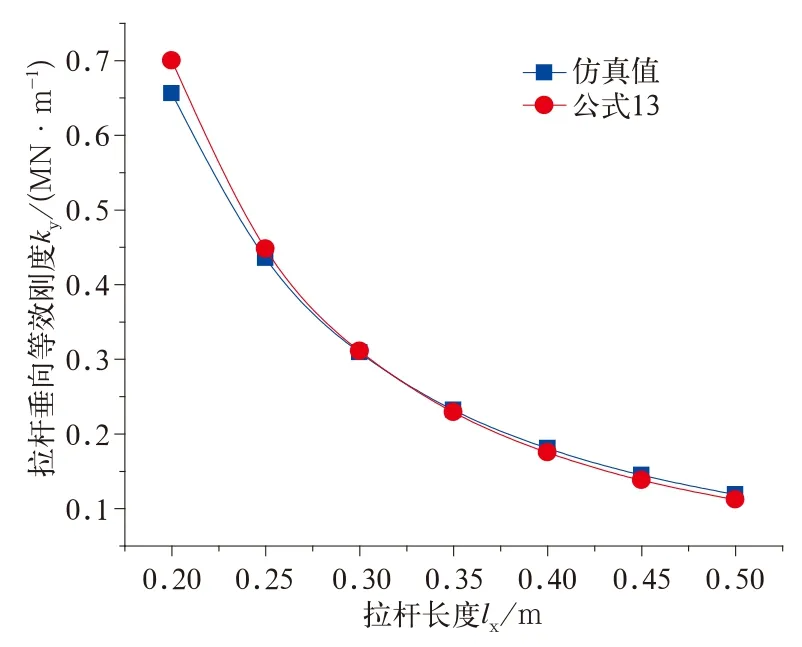
图10 拉杆长度lx对拉杆垂向等效刚度的影响
不对称影响因素b/a(a+b=lBC=0.3 m)对拉杆横向和纵向等效刚度的影响如图11、12所示,当b/a为正时,即∠CAB>90°,当b/a为负时,即∠ACB>90°,当b/a为零时,即∠ACB=90°。
当拉杆对称时(a=b),拉杆BC边长lBC对拉杆横向等效刚度的影响如图13所示。
由上可得:拉杆纵向长度lx对拉杆的横向和垂向等效刚度影响明显,当lx增加时,拉杆横向和垂向等效刚度显著减小;拉杆不对称因素对拉杆的横向、垂向等效刚度无影响,而对拉杆纵向等效刚度影响明显,随着不对称因素的增加,拉杆纵向等效刚度先增大后减小,最后趋于平稳;当拉杆形状为直角时,拉杆纵向等效刚度减小为对称时的一半;拉杆的横向等效刚度随着拉杆横向长度增加而呈线性增加。
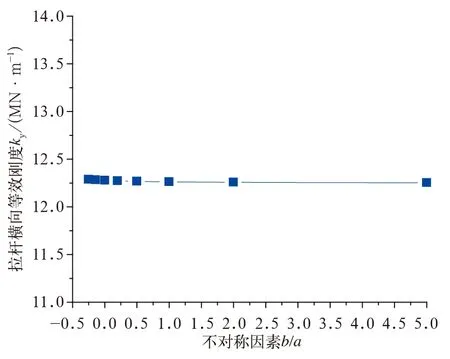
图11 拉杆不对称影响因素b/a对拉杆横向等效刚度的影响

图12 不对称影响因素b/a对纵向等效刚度的影响
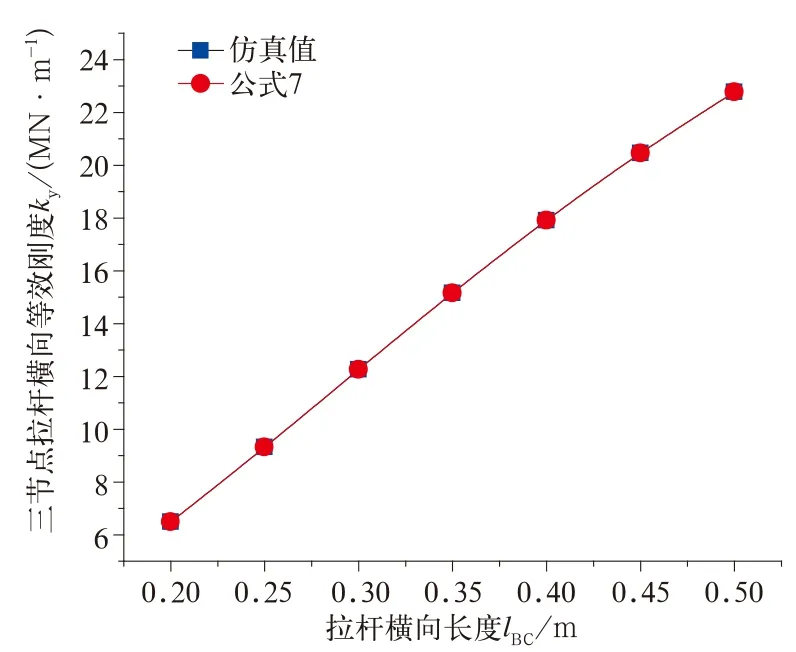
图13 拉杆BC边长lBC对拉杆横向等效刚度的影响
3 结 论
首先推导了三节点单拉杆的等效刚度的理论计算公式,并通过多体动力学软件SIMPACK验证了所得理论公式的正确性,最后对所得理论计算公式进行了工
程简化,得到了满足工程需求的简化计算公式(11)、式(12)、式(13),进而为该类型的轴箱定位设计提供了理论指导。 同时得到如下结论:
(1)拉杆纵向长度lx对拉杆的横向和垂向等效刚度影响明显,当lx增加时,横向和垂向等效刚度显著减小。
(2)拉杆不对称因素对三节点拉杆的横、垂向等效刚度几乎影响,而对拉杆纵向等效刚度影响明显,随着不对称因素的增加,拉杆纵向等效刚度先增大后减小,最后趋于平稳;当拉杆形状为直角时,拉杆纵向等效刚度减小为对称时的一半。
(3)拉杆的横向等效刚度随着拉杆横向长度的增加而近似呈线性增加。
[1]王安国,吕成吉,王靖.CRH5A型动车组转向架一系双拉杆定位刚度及性能影响[J].大连交通大学学报,2013,34(5):33-36.
[2]缪炳荣,方向华,傅秀通.SIMPACK动力学分析基础教程[M].成都;西南交通大学出版社,2008.
Study on Positioning Stiffness of Three-node Pull-rod Axle-box
ZHANGJiang1,LIUGaokun2,LIUQiang3
(1Knorr Equipment (Suzhou) Co., Ltd., Suzhou 215011 Jiangsu, China;2China Railway Fourth Survey and Design Institute Group Co., Ltd., Wuhan 430063 Hubei, China;3State Key Laboratory of Traction Power, Southwest Jiao Tong University, Chengdu 610031 Sichuan, China)
This paper deduces the theoretical calculation formula of positioning stiffness of three-node single pull-rod axle-box at first. Then established the physical model of three-node simplex pull rod, and the correctness of the theoretical formula is verified by this model, and the influence factors of rod equivalent stiffness are discussed simultaneously. It turned out that: The theoretical calculation formula of positioning stiffness of three-node single pull-rod axle-box can reflect the real situation, the deviation of the lateral, longitudinal and vertical equivalent stiffness of the rod were within 10%; the longitudinal length of the rod made a big difference to lateral and vertical equivalent stiffness, and as the length increased, lateral and vertical equivalent stiffness was significantly reduced; Asymmetry factors on the lateral, vertical equivalent stiffness of the pull rod had no effect on lateral and vertical equivalent stiffness, but having significant impact on longitudinal equivalent stiffness, moreover the longitudinal equivalent stiffness increased firstly and then decreased ,at last it leveling out during the increasing of asymmetry factors; the lateral equivalent stiffness increased linear with the increase of rod lateral length approximately.
three-node rod; axle-box positioning stiffness; pull-rod equivalent stiffness
1008-7842 (2016) 03-0011-05
男,工程师(
2015-12-20)
U260.331+.7
Adoi:10.3969/j.issn.1008-7842.2016.03.03

