舱体入水工况参数对冲击特性的影响分析

李建阳,邢伟,宋世鹏,周宇,虞明根

(1.航天工程大学士官学校,北京102249;2.北京特种工程设计研究院,北京100028)

0 引言

载人飞船返回舱可采用陆上或者海上回收,目前,我国神舟号飞船采用的是降落伞和反推火箭陆上回收方式,而美国的载人飞船主要采用海上回收[1-2]。随着载人航天工程的发展,在未来的空间应用中要求调高轨道倾角,返回时陆上着陆场的选择将变得十分困难。随着我国海军力量的增强,未来我国返回舱选择海上回收方式将变为可能[3]。采用海上回收有其固有的优点,首先海洋面积比陆地面积大得多,其次海水是良好的缓冲介质,再者海面相比陆地来说天然危险物和人为危险物明显减少。

神舟号飞船入水冲击试验表明[4],返回舱入水过程中可能会出现高达数十倍重力加速度的冲击加速度峰值,冲击载荷受垂直入水速度、入水角度等因素的影响[5]。超过允许范围的冲击载荷不仅会损坏舱内设备,而且还可能危及航天员的生命安全,关系到整个载人航天任务的成败,因此,在新型舱体的设计阶段需要对入水冲击特性进行充分研究。

为了分析和验证载人飞船返回舱的入水冲击性能,包括“阿波罗号”“神舟号”、“猎户座”等在内的返回舱都进行了缩比模型或样机模型物理实验[4,6-7]。同时以Von Karman[8]和Hirano等[9]为代表的学者在结构入水冲击问题解析计算方面也做了一些研究。截至目前,实验依然是研究入水冲击问题最主要的手段。然而实验需要制造样机、模型,乃至建设专门的场地,成本高、周期长。计算机仿真分析由于其经济性、灵活性和可重复性,能够弥补实验方法的不足,在返回舱入水冲击问题的研究上也逐渐得到应用[10]。

本文运用ALE算法建立舱体-流体有限元模型,并通过理论计算结果验证该模型的有效性,通过有限元模拟舱体入水过程,研究几个舱体入水工况参数对冲击特性的影响,为结构设计及各项指标和方案的科学论证提供理论依据和技术方法。

1 球底结构入水冲击理论计算方法

根据Von Karman基于动量守恒建立的入水问题物理模型[8],得出球形大底的舱体入水时的冲击载荷计算方法。

根据动量守恒原理

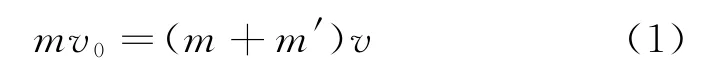
式中,m为舱体质量,m′为附加质量,v0为舱体初始速度。

基于Von Karman理论,舱体入水附加质量为入水物体与静止水面交界的圆盘附加质量的一半,而圆盘的附加质量为

式中,r为舱体触水面圆半径,可表示为

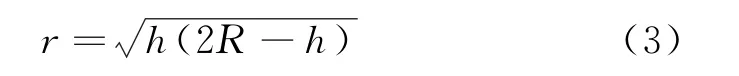
式中,R为球底半径,h为入水深度。

因此,舱体球形大底入水时的附加质量可写成

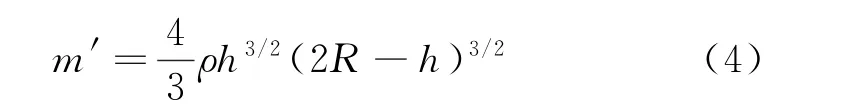
引入量纲为1的参数

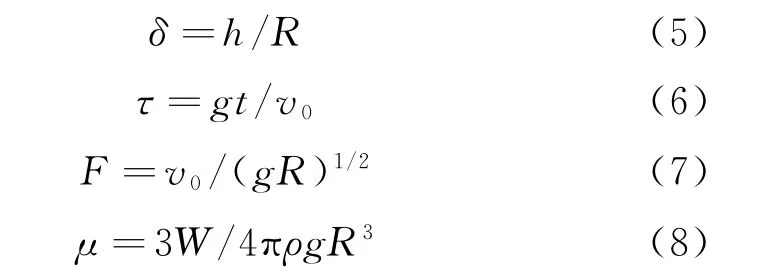
式中,W为舱体质量。

将以上参数均代入动量守恒等式中,得到

由于δ≪1,进行积分可得

也可以求导得出二次导数

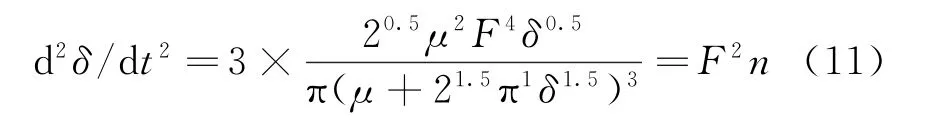
式中,n为加速度过载,是g的倍数。

2 舱体-流体有限元建模

2.1 舱体模型

舱体入水时降落伞和舱体共同起作用,称为降落伞-舱体系统。本文研究的舱体质量不超过5.5t,舱体高度约为4m,底部回转半径约2m。为了简化数值仿真模型,这里仅仅分析舱体在给定速度下入水过程,将舱体简化为刚体,因此只考虑舱体结构外形,建立舱体三维实体模型,采用4节点壳单元对舱体进行网格划分,网格尺寸底部最大为230mm,舱体网格数量为1424,舱体有限元模型如图1所示。

图1 舱体有限元模型Fig.1 Finite element model of recovery module

2.2 流体有限元模型

对于入水过程中的空气部分,需要考虑气动升力对舱体的影响,水的部分需要考虑不同水深时的静水压强,准确的材料本构与状态方程的定义是关键。RADIOSS中有可用于模拟三相材料的本构模型,可用来定义固体、液体、气体和爆炸物等,其允许在一个网格中存在多种物质材料,材料参数的调整可选择相应的状态方程来描述压力与体积的关系。

将流体模型的网格区域划分为两部分,上部分为空气域,下部分为水域。为了模拟无限水域,在流体单元的边界上定义无反射边界条件。空气域尺寸为9m×9m×4.3m,网格数量为737280,水体尺寸为9m×9m×7.5m,网格数量为2359296,都采用solid单元划分网格。舱体-流体有限元模型如图2所示。

图2 舱体-流体有限元模型Fig.2 Finite element model of module＆fluid

2.3 接触类型选择

采用专用的流固耦合接触类型TYPE18进行定义,流体、固体可在空间上重叠,其中舱体需设置为“master”,流体部分设置为“slave”。接触刚度St的定义非常重要,尤其是网格比较稀疏时,可遵循式(14)的经验公式。

式中,Gap为推荐按照接触区域法向方向上的流体网格尺寸的1.5倍,ρ为最重的流体密度,S el为拉格朗日描述处的一个网格的面积,V为所考察的问题速度。

3 舱体入水过程模拟及有限元模型验证

3.1 舱体入水过程模拟

通过定义舱体与流体域相互之间的接触,施加边界条件,为了提高计算效率,在舱体与水面之间设置很小的距离,并且给舱体设置一个入水初速度,舱体入水过程模拟采用显式有限元方法进行求解。

以某工况为例,舱体质量为5.5t,入水初速度为8m/s,仿真获得的包括舱体质心位移、速度和垂向冲击加速度在内的舱体入水冲击特性曲线如图3所示。

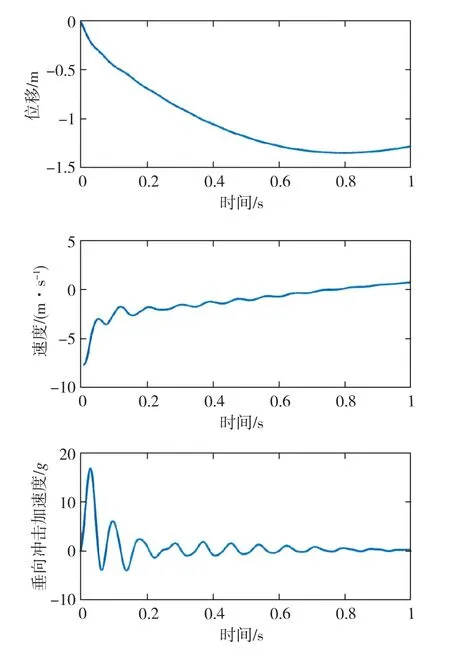
图3 舱体入水冲击特性曲线Fig.3 Impact characteristic curves of water entry

图4给出了舱体入水过程仿真中的几个典型时刻水体压力云图截图,其分别对应着:(a)0ms,仿真开始时刻;(b)10ms,舱体接触水面时刻;(c)27ms,垂直方向加速度最大时刻;(d)70ms,加速度曲线第2个峰值时刻;(e)90ms,加速度曲线第3个峰值时刻;(f)800ms,舱体质心位移最大时刻。

通过仿真计算结果可知,舱体入水最大深度1.4m,出现在入水后800ms时刻,此时舱体质心速度降为0,舱体由于自身浮力开始向上运动;舱体质心垂直方向冲击加速度峰值为16.9g,出现在27ms时刻,第2个峰值6.2g,出现在70ms左右。

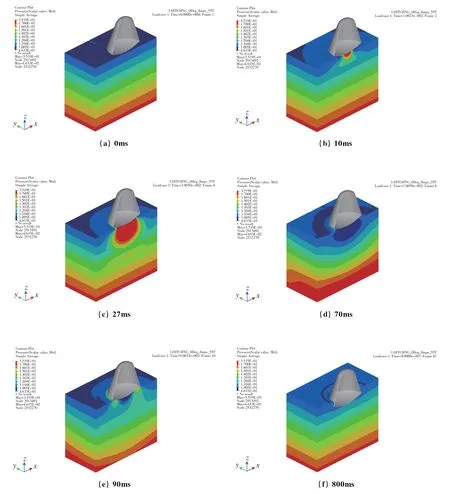
图4 几个典型时刻水体压力云图Fig.4 Pressure contour of water at typical moments

3.2 舱体-流体有限元模型验证

采用有限元和理论计算方法进行了入水初速度分别为6m/s、8m/s和10m/s的入水过程模拟,其中舱体质量为5.5t、入水角度为0°。两种方法得出的冲击加速度峰值如表1所示。

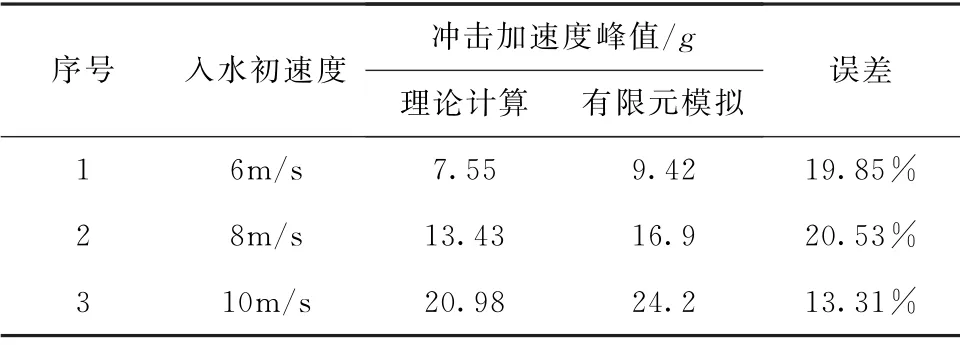
表1 有限元模拟与理论计算结果对比Tab.1 Comparison of finite element simulation results and theoretical calculating results

从表1可以看出,3个工况的计算结果对比误差最大不大于21%,在可接受范围内,说明所建立的舱体-流体有限元模型计算结果具有一定的可信度。其中理论计算结果要小于有限元模拟结果,这是由于Von Karman法没有考虑液面隆起现象,促使沾湿面比实际情况小,故计算得出的冲击加速度偏小。

4 舱体入水工况参数对冲击特性的影响

在实现舱体入水动态仿真的基础上对影响舱体入水冲击的因素进行分析和比较。本文选取舱体的入水冲击加速度值作为分析和比较的目标值。首先,最大冲击加速度点是舱体入水过程中工况最为苛刻的,比较具有代表性;其次,相对于冲击压力等,有限元的建模计算对加速度的模拟更为真实准确。

关于可能影响舱体入水冲击的影响因素,根据试验以及研究的经验,大致有3个影响因素,包括垂直速度、水平速度,以及入水角度。其中水平速度是由舱体落点区域的风速决定的,其余2个因素均是人为可以控制的。因此,本文对垂直速度和入水角度对冲击特性的影响进行研究。

4.1 垂直速度对冲击响应特性的影响

对于垂直速度,选取6m/s、8m/s、10m/s 3种工况,舱体以入水角度为0°、质量为5.5t进行模拟,得到的冲击特性曲线如图5所示。

图5 不同入水速度舱体入水冲击特性曲线对比Fig.5 Comparison of the impact characteristic curve in different water entry velocities

舱体垂直速度6m/s时冲击加速度峰值为9.4g,8m/s时冲击加速度峰值为16.9g,10m/s时冲击加速度峰值为24.2g。最大入水深度6m/s时为1.2m,8m/s时为1.4m,10m/s时为1.5m。由此可见,随着垂直速度的增大,冲击加速度峰值明显增大,最大入水深度也变大,舱体速度降为0即达到最大入水深度的时刻随着垂直速度的变大而略微提前。

4.2 入水角度对冲击响应特性的影响

舱体在入水前的姿态不同,会对舱体入水过程产生不同的影响。选取4种不同的舱体入水角度:0°(大端入水)、20°、40°、60°,入水姿态如图6所示。

通过上述不同入水角度模拟,考察其对舱体入水冲击特性的影响。图7给出了不同入水角度舱体入水冲击特性对比。

从图7中的对比结果可以看出,由于舱体在初始冲击时速度最大,冲击入水的深度也最大,后期舱体浮动的幅值会逐渐减小。入水角度为0°、20°、40°和60°时,舱体的最大入水深度分别为1.4m、1.6m、2.1m、2.9m。随着入水角度的增大,舱体的入水深度也越大。舱体的入水角度越大,水更容易沿着舱体表面发生飞溅,舱体在入水过程中受到的水的阻力就会减小,入水深度也就越大。

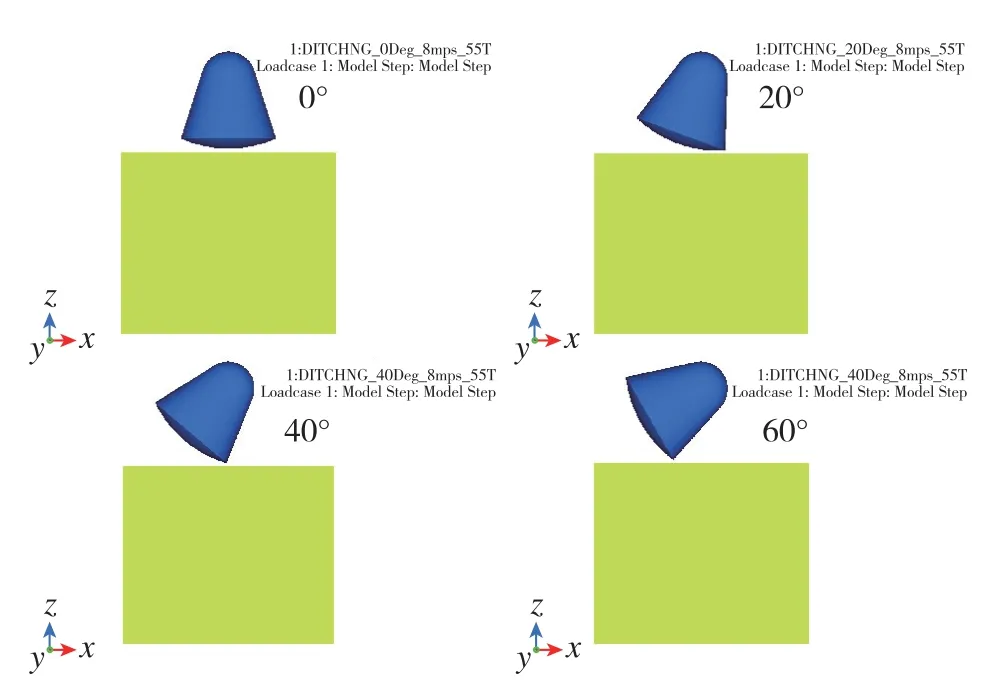
图6 舱体不同入水角度示意图Fig.6 Schematic diagrams of different water entry angles

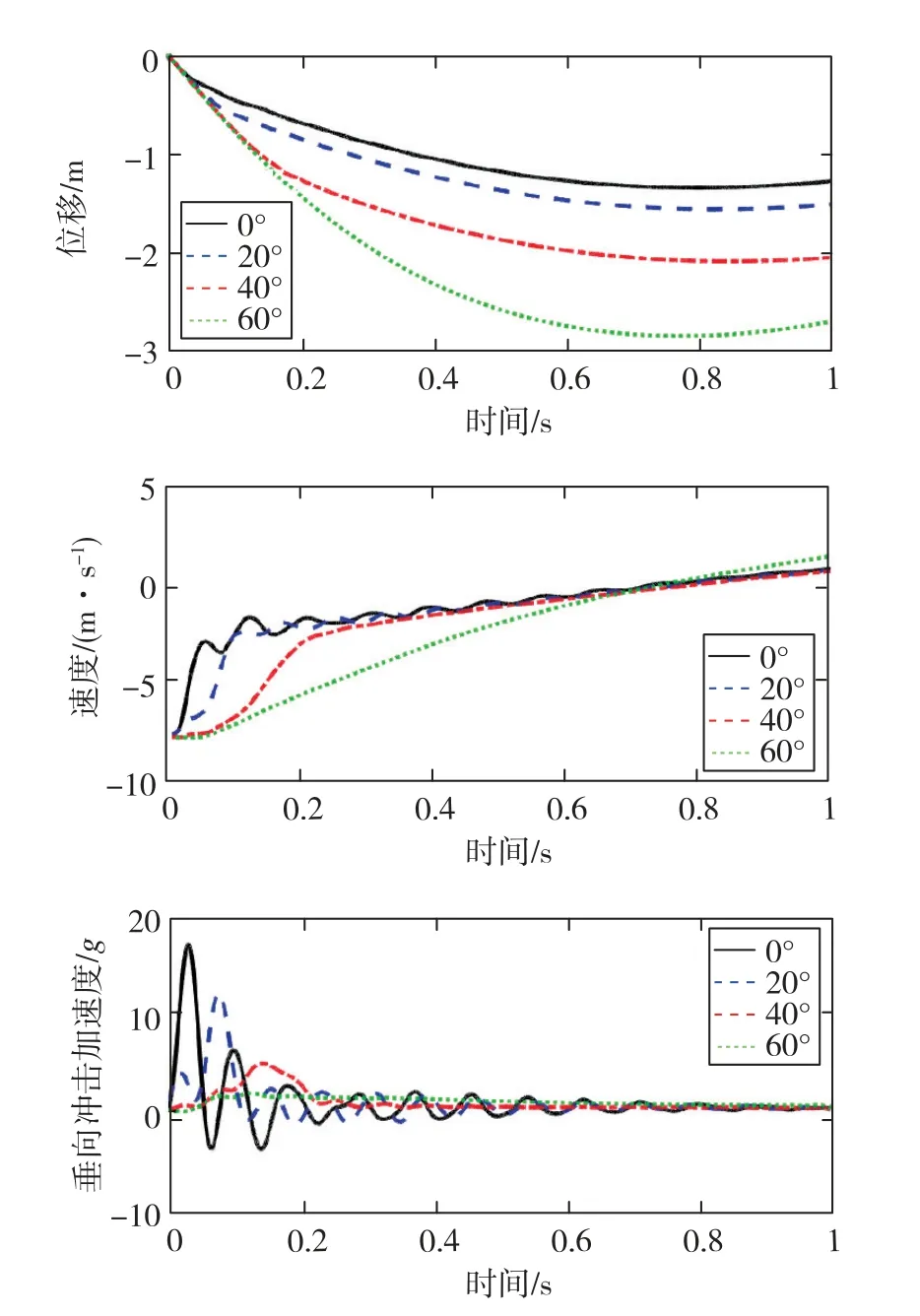
图7 不同入水角度舱体入水冲击特性曲线对比Fig.7 Contrast of the impact characteristic curve in different water entry angles

由于刚入水时舱体受到的冲击力会比较大,速度减小幅度较大,随后舱体遭受的冲击力逐渐减小,速度较小的趋势渐缓,当减到0m/s时达到最大入水深度,然后上浮,随后速度在0m/s附近上下浮动,幅值逐渐减小。不同入水角度对舱体质心速度的影响主要是入水的初始阶段,角度越小,速度减小得越迅速。

当舱体接触水面后,加速度会迅速增大,达到峰值后就逐渐减小。入水角度为0°、20°、40°和60°时,舱体垂向冲击加速度峰值分别为16.9g、12.0g、4.8g和1.8g。这是由于舱体入水角度越大,水更容易沿着舱体表面发生飞溅,舱体受到水的阻碍越小,冲击加速度峰值也就越小。

5 结论

基于ALE方法建立舱体-流体有限元模型,通过理论计算方法验证该模型的有效性,最后通过对比研究不同垂直速度和入水角度对冲击特性的影响。结果表明,舱体垂直速度与冲击加速度峰值、最大入水深度成正比;舱体以一定角度入水时,在入水初期,加速度会迅速增大到最大值,随后逐渐减小,速度在此过程中会迅速减小,角度也有明显的变化。本文的研究可以为新型舱体结构设计及各项指标和方案的科学论证提供理论依据和技术方法,为物理试验提供指导,缩短开发周期。