基于特征值拟合优度的频谱感知算法研究

李 贺， 赵 文 静， 罗 雪 松， 刘 畅， 邹 德 岳， 金 明 录

( 大连理工大学 信息与通信工程学院, 辽宁 大连 116024 )

0 引 言

随着无线宽带和多媒体用户市场的迅速扩大以及高数据速率的应用，固定的频谱分配策略导致的可用频谱资源使用效率低和频谱资源匮乏给无线通信网络5G甚至是6G带来了很大挑战.认知无线电作为5G关键技术，允许次用户使用授权主用户的空闲频谱进行机会通信，这是缓解频谱资源紧缺的一项有前途的技术[1].频谱感知是认知无线电技术的一项基本任务，它的目的是在特定地理维度获取授权频谱使用和主用户存在的认知信息.当主用户处于激活状态时，认知用户必须以较高的概率检测到主用户的存在，并在一定时间内清空信道或降低传输功率.然而，错综复杂的实际场景给频谱感知带来了很大挑战，也促进了认知无线电技术的不断发展[2-4].

在过去的10年中，人们提出了许多频谱感知算法.在这些算法中，因计算复杂度低和硬件实现简单，能量检测(energy detection，ED)算法得到较为广泛的使用[5].能量检测算法不需要知道主用户信号参数特征信息，对独立同分布(i.i.d)信号检测具有最优检测性能，但对相关信号的检测性能较差.为了克服能量检测算法的这一缺点，Zeng等[6]提出了基于样本协方差矩阵最大特征值检测(maximum eigenvalue detection，MED)算法.由于协方差矩阵能够捕获信号样本间的相关性，该算法对相关信号的检测优于传统能量检测算法.MED算法也被应用于其他场景，并获得了较好的检测性能[7-9].

ED算法和MED算法不需要已知信号的先验信息，但都需要已知噪声功率作为检测前提.在实际系统中，噪声随时间的变化而变化，导致了信噪比墙现象的存在和虚警概率的增加.为此，人们广泛研究了不需要已知噪声功率的全盲检测算法，包括最大最小特征值检测(maximum-minimum eigenvalue，MME)[10]、算数几何平均算法检测[11]和特征值加权检测[12].使用所有特征值的检测算法在矩阵维数较大的情况下具有较高的计算复杂度，因此需要采用最大最小特征值的频谱检测算法.在这些基于特征值的检测算法中，MME算法检测效果相对较好且具有较低的计算复杂度.

另一方面，频谱感知可以表述为一种拟合优度(goodness-of-fit，GoF)检测问题[13]，它不需要主用户信号的任何先验信息，只需要已知噪声的统计分布，通过检验观测到的样本是否服从该噪声分布来进行判决.在GoF理论框架下，人们提出了许多检测算法，如Anderson-Darling(AD)检测[14]、单边右尾AD(unilateral righttail Anderson-Darling，URAD)检测[15-17]、Cramer von Mises(CM)检测[14]和Kolmogorov-Smirnov(KS)检测[18].对于拟合优度检测问题，人们研究的关注点在于拟合度量和拟合统计量.

这些已有的算法大多以信号样本或能量作为拟合统计量，在检测动态相关信号时，性能会急剧下降.如果利用基于特征值的统计量来捕获信号的相关性，可以进一步提高检测性能.贺亚晨等[16]提出了一种新的基于样本协方差矩阵最大特征值的拟合优度检验频谱感知算法.该算法利用随机矩阵理论分析样本协方差矩阵最大特征值的分布，通过GoF检验检测主用户的存在，在动态信号下能表现出良好的检测性能.

但是基于最大特征值拟合优度的检测仍然存在噪声不确定性问题，实际应用受到限制.为此，本文着重研究特征值域的拟合优度检测问题，采用基于最大最小特征值之比作为拟合统计量的全盲拟合优度检测算法，以便克服噪声不确定性问题.在随机矩阵理论框架下，基于最大特征值的Tracy-Widom分布，分析所提算法的检测概率、虚警概率和判决门限.最后，通过仿真实验说明新算法的有效性和性能提升.

1 系统模型和拟合优度检测

图1是一个典型的多天线频谱感知场景，其中随机分布一些单天线主用户和一些多天线次用户，次用户可以根据接收到的信号样本进行频谱感知.如果主用户开始广播信号，那么次用户就能够接收到主用户信号和噪声信号，否则只接收噪声信号.

设每个次用户配备M个阵元的线天线阵，设有D(D≤M)个不相关的PU信号分别来自不同方向的发射机，则在次用户接收天线处的频谱感知问题实际是对某一授权频段是否可用的判断，可以表示为如下的二元假设检验问题[14]：

(1)

同一时刻的采样数据可以表示为如下的向量形式：

x(k)=(x1(k)x2(k) …xM(k))T
hj(k)=(h1j(k)h2j(k) …hMj(k))T
n(k)=(n1(k)n2(k) …nM(k))T
s(k)=(s1(k)s2(k) …sD(k))T

(2)

则式(1)的频谱感知问题可以表示为如下的二元假设检验问题：

H0：x(k)=n(k)
H1：x(k)=H(k)s(k)+n(k)

(3)

其中H(k)=(h1(k)h2(k) …hD(k)).如果假设信道为慢衰落，则信道矩阵为常数阵，表示为H.

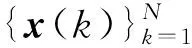
假设FX(x)表示观测值xi(k)的经验累积分布函数，可以定义为

FX(x)=|{(i，k)：xi(k)≤x，1≤i≤M，1≤k≤N}|/MN

(4)

其中对任意的有限集合S，|S|表示集合S的基数.

在零假设下，随着拟合对象数的增多，接收信号经验累积分布函数FX(x)会逐渐收敛于噪声信号的实际累积分布函数F0(x)，即当MN足够大时，在零假设成立的情况下，FX(x)会非常接近F0(x)，如果FX(x)显著偏离F0(x)，则认为零假设H0不成立，说明存在主用户信号.怎样度量两种分布F0(x)和FX(x)之间的距离，是拟合优度检测算法的关键.随着数学统计理论的发展，人们提出了许多度量分布F0(x)和FX(x)之间距离的优秀算法，统称为拟合准则.常用的GoF检测的拟合准则包括KS准则、CM准则和AD准则等.拟合优度假设检验问题可以表示为如下的二元假设：

H0：FX(x)=F0(x)
H1：FX(x)≠F0(x)

(5)

基于拟合准则计算得到FX(x)与F0(x)的判决统计量T，通过与判决门限γ进行比较，当T<γ时，就接受H0假设，认为不存在发送信号；否则拒绝H0(即接受H1)，认为存在发送信号.

除了信号样本之外，还有样本能量和其他量(如特征值)都可以作为拟合统计量.一般情况下，设T(L)={t1，t2，…，tL}为L个时间样本的观测统计量，其累积分布函数记为F0(t)，则零假设可以表示为

H0：T(L)～F0(t)

(6)

因此，主用户存在(H1)等价于T(L)不是服从分布F0(t)的序列.

拟合优度检测算法的设计除了拟合统计量的选择之外，重要的是拟合度量(拟合准则)的选择.基于文献[16-17]的考虑，本文也选择URAD拟合准则.在URAD拟合准则下，判决统计量定义为

(7)

其中L为样本数.另外，FT(t)表示拟合统计量tl，l=1，2，…，L的累积经验分布函数.对于有限数量的拟合统计量，TURAD可以写成

(8)

其中Zl=F0(tl).因此，通过比较TURAD和判决门限γ进行检测判决.如果TURAD>γ，拒绝零假设H0，即主用户信号存在；否则，该通道未被使用.

2 基于最大最小特征值的GoF检测

首先介绍样本协方差矩阵特征值的分布，然后简单介绍基于最大特征值的拟合优度检测算法，最后提出改进的基于特征值的拟合优度检测算法.

2.1 样本协方差矩阵特征值分布

协方差矩阵能够捕获信号样本间的相关性，且广泛应用于信号检测领域，为此许多协方差矩阵的估计方法被提出，其中样本协方差矩阵是最大似然估计.考虑N个采样序列，接收信号的样本协方差矩阵可以表示为

(9)

其中(·)H表示共轭转置.在H0假设下，即当不存在发送信号时，Rx(k)=Rn(k)，如下式所示：

(10)

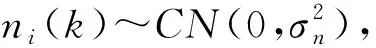
(11)

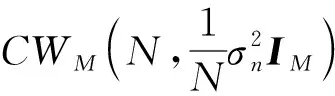
根据随机矩阵理论可知，Wishart随机矩阵特征值的联合概率密度分布函数(PDF)有着非常复杂的表达式，并且其特征值边缘PDF也还没有找到一个合适的表达形式.幸运的是Johnstone和Johansson等已经对Wishart随机矩阵的最大特征值分布做了一定的研究[10-11]，研究成果描述如下：

由定理1可知，在主用户信号不存在的情况下，样本协方差矩阵最大特征值的归一化值服从Tracy-Widom分布，表现出了一种特定的统计特性.

对最小特征值则有如下的结论：

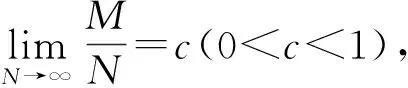
2.2 基于特征值的GoF检测算法

由定理1可知，在假设H0下，样本协方差矩阵最大特征值的归一化值服从TW分布FTW1(t)，因此根据URAD拟合准则可以得到基于最大特征值的拟合优度检测算法.

(12)

其中Zl=F0(tMED)=FTW1(tMED).

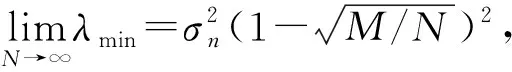
(13)

因此，根据定理1和定理2，可以得到最大最小特征值之比的分布函数如下：

F0_MME=Pr{λmax(Rx(N))≤βλmin(Rx(N))}=

(14)

其中F1(·)是一阶TW分布的累积分布函数(CDF)，β为门限.

根据式(8)的URAD拟合准则，可以得到基于最大最小特征值的拟合优度检测算法.步骤如下：

步骤1数据处理.将长为N的接收数据均分为长为Ns的L段(Ns=N/L)，即

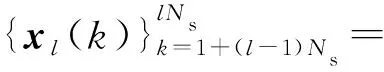
x(2+(l-1)Ns)，…，

x(lNs)}

(15)

步骤2计算各部分的样本协方差矩阵.

(16)

步骤3计算每个样本协方差矩阵的拟合统计量.

(17)

步骤4按升序排列拟合统计量.假设已排序的拟合统计量是

tMME(1)≤tMME(2)≤…≤tMME(L)

(18)

步骤5计算判决统计量.

(19)

其中Zl=F0(tMME)=FTW1(tMME).

步骤6判决.如果TMME-GoF>γ，那么信号存在；否则，信号不存在，γ是判决门限.

注意到，当数据分组数L=1时，即数据不分割，判决统计量为TMME-GoF=-1-ln(1-Z1).由于函数ln( )和F1( )都是单调函数，则MME-GoF算法的判决统计量TMME-GoF是MME的判决统计量TMME的单调函数，此时MME-GoF算法和MME算法等价，MME算法可以看作是MME-GoF算法的特例.这也说明研究基于特征值的拟合优度检测算法有较好的理论意义.

3 性能分析

检测概率(Pd)与虚警概率(Pf)是评价检测方法性能的两个重要指标，可以表示为

Pd=Pr{T>γ|H1}
Pf=Pr{T>γ|H0}

(20)

其中T表示由式(19)给出的判决统计量，γ为判决门限.为了计算检测概率和虚警概率，需要求解判决统计量T在H1假设和H0假设下的概率分布函数.从式(19)可以看到，求解判决统计量T的概率分布函数很难.为此本文利用中心极限定理简化推导所提算法的检测概率、虚警概率和判决门限.

根据式(1)中的系统模型和最大最小特征值拟合优度检测算法，所划分的L个样本协方差矩阵是独立同分布的.因此，tMME(1)、tMME(2)、…、tMME(L)可视为i.i.d序列.在这种情况下，ln(1-Z1)，ln(1-Z2)，…，ln(1-ZL)也是i.i.d序列.利用中心极限定理，TMME-GoF近似服从如下分布：

TMME-GoF～N(-L-L×E[ln(1-Zl)]，L×Var[ln(1-Zl)])

(21)

其中E[·]和Var[·]表示均值和方差；N(a，b)表示均值为a、方差为b的真实高斯分布.注意，ln(1-Zl)的PDF闭式表达式很难求出.因此，均值和方差的近似值可以通过蒙特卡罗方法得到.

Pf_MME-GoF=Pr{TMME-GoF>γ|H0}=

(22)

Pd_MME-GoF=Pr{TMME-GoF>γ|H1}=

(23)

对于任何给定的Pf_MME-GoF，判决门限γ可以通过下式计算：

(24)

4 仿真与讨论

本文给出一些仿真结果对所提算法的性能进行分析讨论.没有特别说明，假设有4个PU源信号通过平坦瑞利衰落信道传输，被具有4个天线阵元的多天线接收机系统接收.假设样本数量N=100，分段数量L=4，虚警概率为0.1.所有结果通过5 000次蒙特卡罗实验平均得到.与一般文献一样，假设主用户信号服从相关高斯多变量分布，相关矩阵系数定义为(Rx)p，q=0.5|p-q|，其中(·)p，q表示第p行、第q列元素[8].为了比较公平，所有算法都采用URAD方案作为拟合度的度量.

比较分析了最大特征值拟合优度算法(MED-GoF)、最大最小特征值拟合优度算法(MME-GoF)、基于样本的拟合优度算法(SAM-GoF)和基于能量的拟合优度算法(EN-GoF)的检测性能.从图2可以看到，对弱相关性高斯信号，EN-GoF算法优于MED-GoF算法，而MME-GoF算法则接近于SAM-GoF算法.

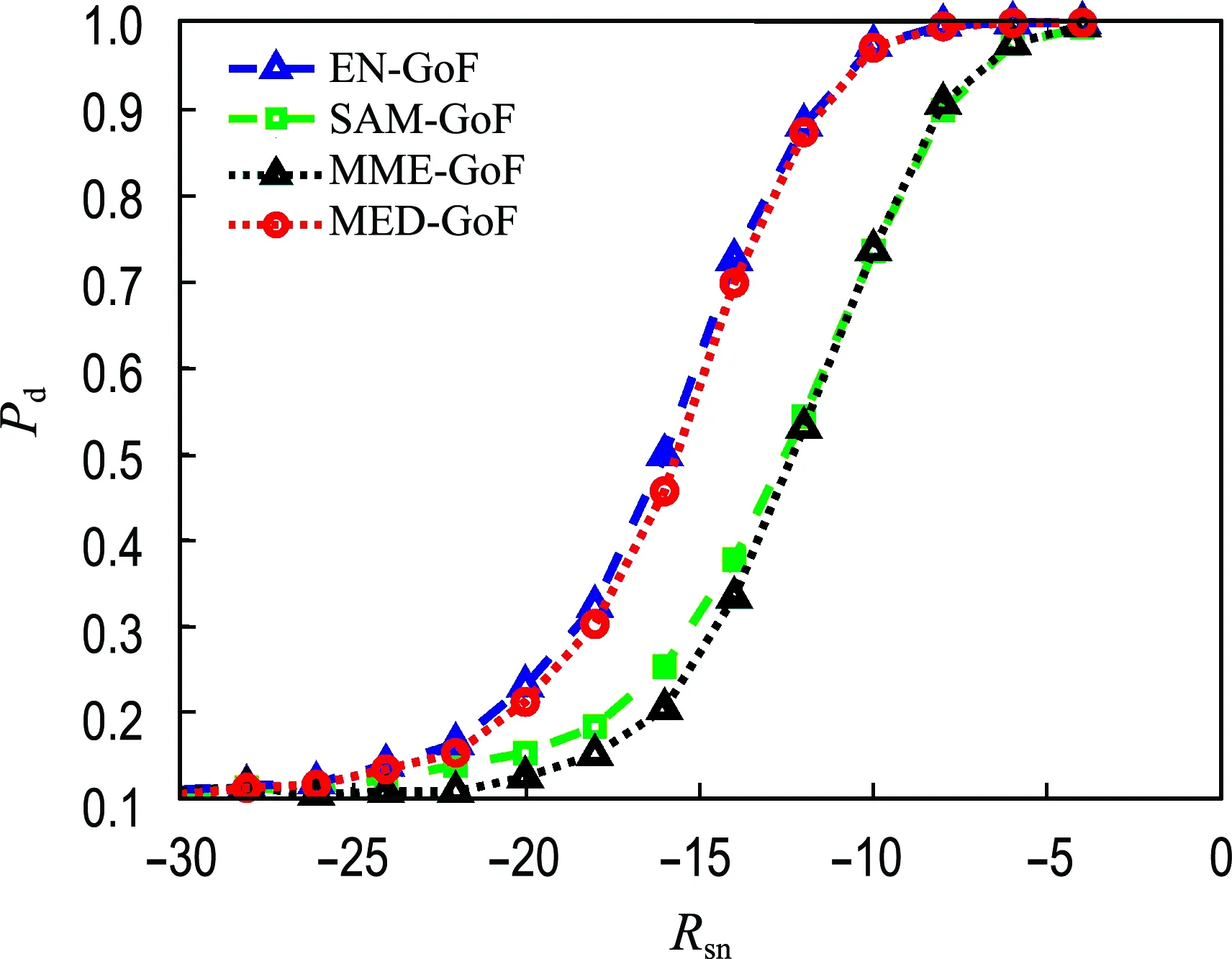
图2 不同拟合优度算法比较(ρ=0.1)

图3给出了在强相关性高斯信号下的检测性能，此时MED-GoF算法优于EN-GoF算法，MME-GoF算法也优于SAM-GoF算法，但是不如EN-GoF算法.

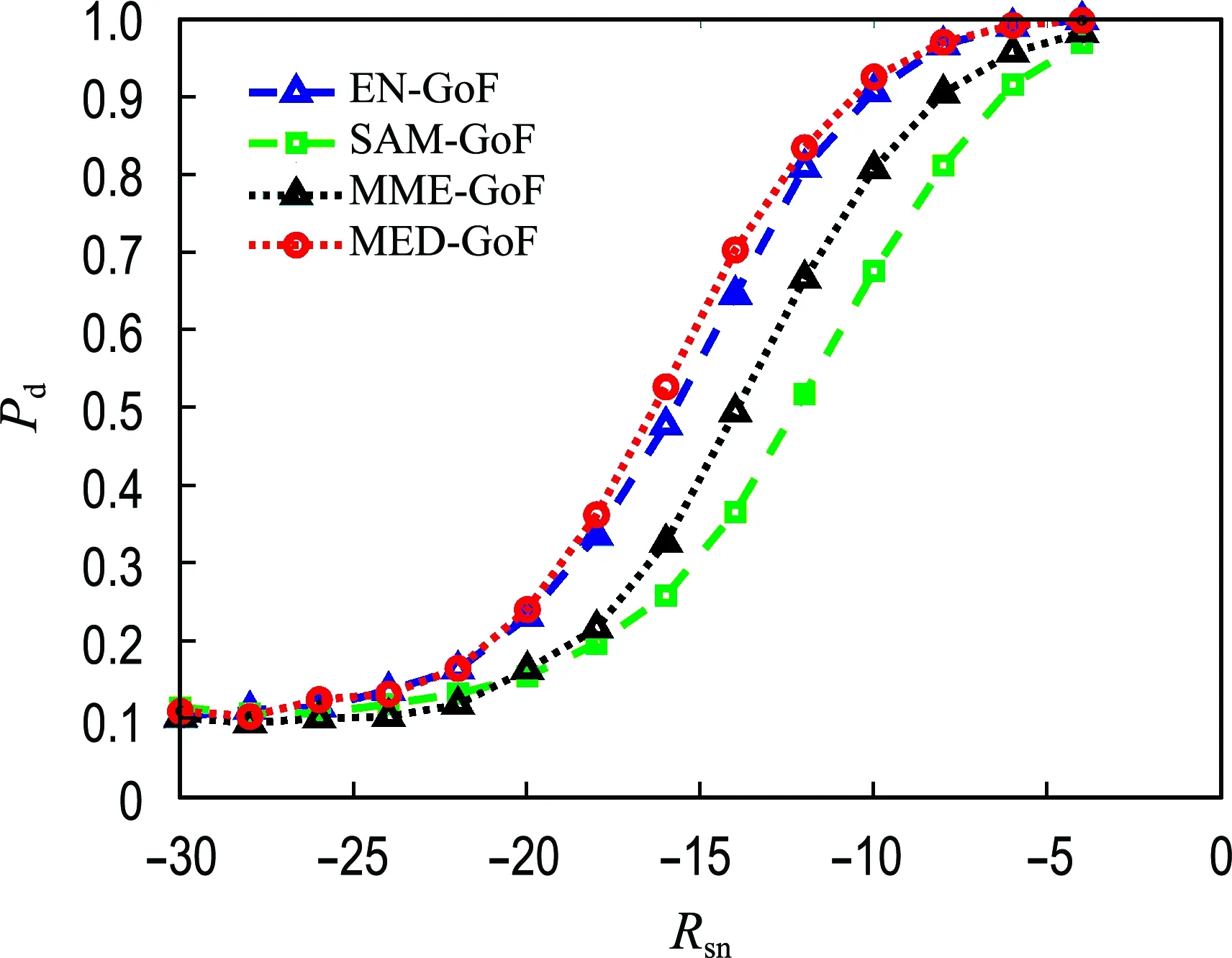
图3 不同拟合优度算法比较(ρ=0.9)

此外，考虑了噪声方差不确定性的影响，将阈值固定为0.1，噪声方差设置为0、1和2 dB，结果如图4所示.可以看到，经典的EN-GoF和SAM-GoF算法与MED-GoF算法都存在噪声不确定性问题，并且在存在噪声不确定性时呈现较高的虚警概率.因此，设计的MME-GoF算法可以实现较高的检测概率，并且对噪声不确定性问题具有鲁棒性.

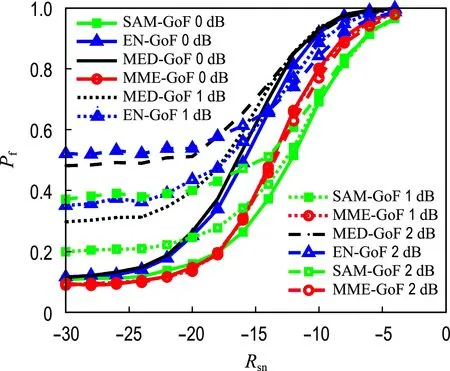
图4 在噪声不确定条件下不同拟合优度算法比较

5 结 语

本文考虑了基于特征值的GoF检测问题，提出了基于MME的GoF检测算法.该算法是一种全盲检测器，能够捕获相关信息以提高检测性能.对所提算法的理论性能进行了相应的分析.最后，仿真结果验证了该算法能够克服噪声不确定性的问题，与现有基于时间样本的GoF算法相比，在高度相关的PU信号情况下，算法实现了性能提高.