基于多约束优化的车门分缝线自动设计方法
靳 春 宁, 周 乐, 谢 悦, 李 宝 军, 王 海 锋
( 1.大连理工大学 汽车工程学院, 辽宁 大连 116024;2.比亚迪汽车工业有限公司汽车工程研究院, 广东 深圳 518000 )
0 引 言
车身零部件设计受到诸多因素的制约,进而成为一个反复尝试、评估与修正的迭代过程.车身零部件总是表现为复杂总成的一部分,与总成内的各种关联附件产生各种约束关系,并形成非常复杂的几何形态.零部件设计与相关附件布置需要考虑较多的内外部因素,既要保证与整车及相关部件的一致性、协调性,还要满足自身的技术与功能要求.国内外的研究者、开发者在这方面也做了很多有价值的工作,Hou等[1]开展了不同级别车型的模块化划分研究,谢晖等[2]基于KBE开发了B柱冲压工艺设计分析系统,但均尚未考虑复杂系统内部不同部件之间的关联设计和约束;丁祎等[3]开发了车门玻璃升降器智能软件,对复杂设计系统正向设计提出的机制和流程大大提高了开发效率;梁礼光等[4]利用参数驱动的方式,建立了车身概念设计参数化车身框架结构系统,基于分层“子结构”的思想对复杂结构进行约束描述;桂春阳等[5]开发了车身薄壁梁形状优化软件,胡斯博等[6]开发了车身主断面测量工具,均以考虑工程制造多约束方法实现特定部件的工程应用,但仅针对单一结构有效,对复杂系统内部较多附件同时设计并不适用.而在复杂车身设计中,对于那些存在较多设计约束的复杂问题,车身工程师更愿意选择常规方式自行解决,其中一个重要原因就是:很多设计工具和设计模块并不能充分描述和解决设计过程中各种复杂因素,虽然计算机的介入带来高效,但这种高效只有建构在复杂工程约束的基础上才有意义.在这类问题上,工程师是万能的,但却是低效的.
总体而言,常规方法面临3个难以克服的障碍:
(1)概念设计中的关联问题.在车身概念设计中由于主体结构设计的不确定性,由设计经验所提出的零部件设计规格和参数会受到其他附件结构尺寸变化以及附件布置方案的影响[3].例如玻璃升降器的系统总成,最终的合理方案直接由玻璃形状、车门形式、车门内外板形状、其他附件尺寸和位置所决定[7];车门分缝线的设计与铰链布置、车门外板及翼子板相对位置、圆角和厚度、车门开度等相关.
(2)二次开发的常见问题.在车身设计相关的设计工具开发中,为避免烦琐的手工迭代,缩短产品设计周期,提高设计效率,二次开发是一种较为典型的手段,但是二次开发缺乏对复杂设计变量和附件间复杂关联与约束的描述.
(3)多约束与多评价指标的问题.车身零部件设计是一个多因素制约和多评价标准的复杂过程.既要满足系统总成中各关联附件设计约束,还应受到自身结构设计中的几何约束、设计意图、工程规则的综合制约.例如:汽车车门玻璃曲面应为具有固定轴线的回转体,而且前后缘应为具有相同导程并且平行的螺旋线[7].
针对以上问题,本文提出一种基于工程多约束的车身零部件设计方法以应对零部件设计过程中的问题.在这个方法中,复杂的设计变量和附件间的复杂关联与约束可以得到很好的描述,与复杂的工程设计更加接近.本文以车门分缝线自动设计工具作为典型案例进行说明.通过Siemens/NX软件平台上的二次开发,完成一个以多约束优化为基础的设计方法,该模块从全局角度考虑更多的约束,与对标的其他车门分缝线设计方法相比,提升能力和适用性.
1 基于工程多约束的设计方法
在车身零部件的概念设计过程中,本文基于多约束优化方法应对车身零部件的各种复杂问题,从一个全局角度考虑更多约束,以优化迭代方法快速进行复杂零部件的关联设计,不仅提高整体开发效率,并且提高实际设计的柔性、可靠性、合理性,本文整体设计流程有以下3个技术关键.
1.1 多约束参数化模型的建立
复杂的车身零部件之间存在不同的内在约束,因此零部件的设计不是独立和笼统的,而是整体和具体的,具体情况需要具体分析.本文尝试基于多约束优化的方法,构造多约束参数化模型,这个参数化模型就结果而言,与给定的设计输入是不匹配的,或者说其参数是不精确的,但从设计逻辑的角度看,其结构合理,表达了系统内部各附件之间的复杂关联和约束,设计意图、几何约束、工程规则都以规则(rule)方式内嵌于其中,已经达成了合理性,如图1所示.后期的优化工作,就是在这个合理性基础上展开的,并在合理性基础上达成精确,实现与给定输入在几何与数字意义上匹配,达成形神兼备的最终设计结果.多约束参数化模型的构建试图追溯设计师原始设计流程,以参数化模型描述不同的零部件结构之间的内在关联,将多种设计约束和评价指标作为约束引入,进而在保持精度的情况下,维持模型的内在关联与合理性.

图1 多约束参数化模型
1.2 优化模型的建立
本文采用Siemens/NX软件平台提供的知识驱动[8]自动化方案中的KF语言来构建这个优化模型.KF语言是一种面向对象的语言,它是一种业界公认的完全基于规则的知识工程[9]编程语言,主要用类来描述,其应用程序无须编译即可运行.利用KF语言,把构建的车身零部件的多约束优化模型写在一个指定的dfa文件中,然后用Siemens/NX提供的优化类ug_optimize[7]改进优化算法进行优化计算.
优化模型的建立就是寻找最佳的优化目标值,因此优化模型的参数设置为优化目标、优化约束、优化变量,具体的零部件设计需要构建具体的优化模型.
1.3 多阶段灵敏度分析
本文基于多约束优化的设计方法,对于复杂的车身零部件结构可能会有几百个工程参数同时进行优化迭代,是一个在多变量、多约束条件下获得最优解的过程,能够保证优化过程合理高效是本文设计方法的关键所在,优化迭代的效率和精度与众多设计参数相关.
首先,在整个优化过程对于兼顾多种约束的复杂零部件模型所包含的众多参数进行多阶段灵敏度分析[10].通过多阶段灵敏度分析确定优化过程中在不同状态下最灵敏的参数[11],优先进行优化.其次,对于多约束优化模型的目标函数收敛速度和优化目标偏差进行预估,如图2所示.
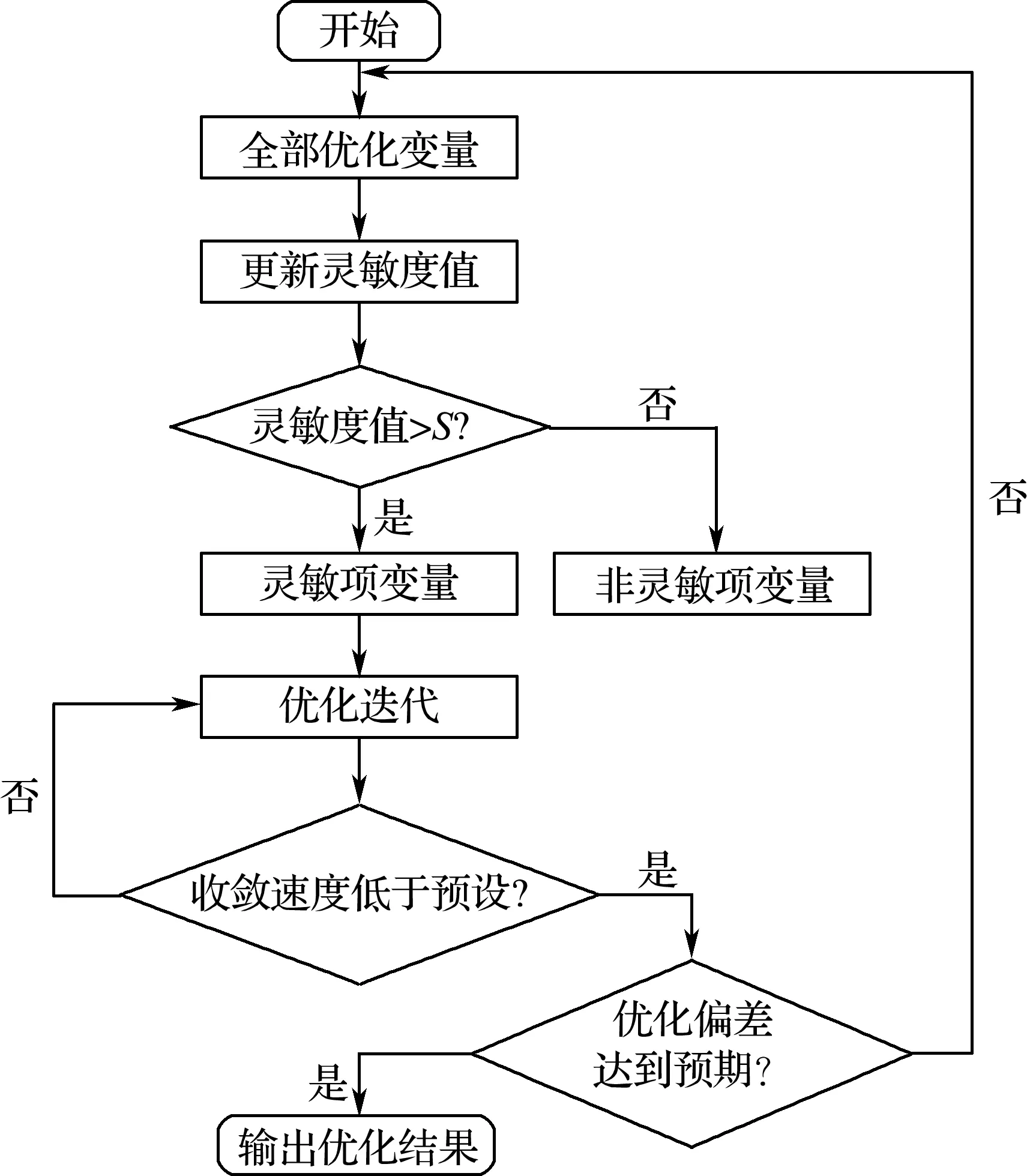
图2 多阶段灵敏度分析流程
2 基于多约束优化的分缝线设计
车门分缝线的设计过程实质是铰链布置、车门及翼子板布置和干涉检查的多约束迭代过程[12].本文方法设计流程包括数据设置、参数获取(同时考虑分缝线设计的多约束工程参数,如铰链的位置参数、车门外板和翼子板的设计参数和位置参数等[13])、断面分析(自动检查车门外板和翼子板、车门外板和铰链的干涉情况;获取断面模型上的前后极限点位置)、分缝线设计(缝合K线、调整分缝线的位置区域),整体设计流程如图3所示;本文主要利用NX Open API、MenuScript、UI-Styler、KF等[3]进行整体架构开发,整体程序设计流程图如图4所示.
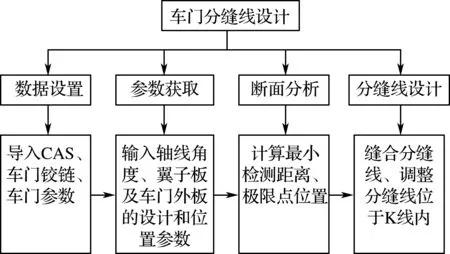
图3 分缝线整体设计流程

图4 程序设计流程图
如果分缝线完全位于位置区域内,意味着该设计合理,反之意味着车门进行转动时会与翼子板和铰链发生干涉,需要调整多约束参数的范围直到分缝线完全位于合理范围内部,但有时需要调整CAS或B柱的结构[14].
2.1 多约束参数化断面模型
对于导入的CAS、车门铰链等构造多约束参数化断面模型,而这个参数化模型是“不精确”的,但是整体结构合理,符合系统内部各附件之间的复杂关联.多约束参数化断面模型内各个附件的参数以及位置关系赋予一个初始值,优化域是根据实际工程设计、制造偏差、装配极限要求进行输入,不同参数的标准参考文献[13,15].在符合优化目标后停止优化,不同的参数都会得到一个最优解,参数化模型的构造过程如下:
步骤1在NX工作环境中构建多约束参数化断面模型.首先构建一系列通过铰链轴线和CAS的多约束参数化断面模型进行优化,考虑到整体设计时间,本文合理选取模型的关键位置,比如上下铰链的安装位置、车身宽度最宽处等16处位置[14].
步骤2使用NX的Expressions编辑功能进行编辑.直接修改编辑断面模型的设计参数,用户可以在表达式间设定各种关联,如图5所示,反映复杂的设计关系.定义多约束参数化断面模型工程参数如下:Xo为铰链轴线到中心位置的X向距离;Yo为铰链轴线到中心位置的Y向距离;Xf为翼子板圆角中心到中心位置的X向距离;Yf为翼子板圆角中心到中心位置的Y向距离;Xd为车门外板圆角中心到中心位置的X向距离;Yd为车门外板圆角中心到中心位置的Y向距离;Tf为翼子板板厚;Td为车门外板板厚;Rf为翼子板圆角圆弧半径;Rd为车门外板圆角圆弧半径;θ为车门旋转角;θin为铰链轴线内倾角;θcas为铰链轴线后倾角.

图5 断面模型中的设计参数
步骤3在侧视图中,定义铰链轴线内倾角θin和后倾角θcas,如图6所示.

图6 铰链轴线内倾角和后倾角
步骤4当设计车门分缝间隙4 mm时,运动过程中车门与车身之间最小间隙要求为1.8~2.5 mm,最小间隙一般出现在车门刚开启时3°~8°及车门外板最大凸弧面处,车门与铰链最小间隙要求为5 mm[15].
在多约束参数化主断面图中利用Expressions 中的Projected Distance Measurement、Minimum Distance Measurement功能检测车门与铰链最小间隙Dd-h、车门与翼子板最小间隙Df-d,如图7所示.

图7 极限位置优化目标
步骤5完成初始多约束参数化断面模型的定义,设计师可以在交互模块界面输入设计参数初始优化域和优化条件,本文主要利用UI-Styler工具结合NX Open API函数构建模块界面和访问Expressions中的复杂设计参数.
2.2 极限位置的优化模型
在多约束参数化断面模型上,粗线表示CAS,Pf和Pd表示翼子板和车门外板的分离点,分离点Pd和铰链轴线确定优化约束条件,分离点Pd作为初始迭代点[14]计算前后极限点,如图7所示.在设计模块中定义优化目标、优化变量、优化约束.本文利用KF语言把多约束参数化断面模型的优化迭代过程写在一个名为section_optimization 的dfa文件中,调用ug_optimize优化类进行优化计算断面前后极限点,本文方法能够同时优化13个参数并且保证车门外板不与周围环境发生干涉,优化模型定义如下:
(1)优化目标:断面图中未发生干涉的最小检测距离Df-d(前极限点)、Dd-h(后极限点).
(2)优化变量:断面模型中影响参数.
(3)约束条件:分离点Pd和铰链轴线的相对位置(前后极限点)、车门最大角度(后极限点).
(4)优化方法:多阶段灵敏度分析的模拟退火算法.
通过多阶段灵敏度分析的优化机制不仅合理保证多个设计参数进行同时优化计算,并且能够合理高效计算车门与周围环境的最小间隙,在确保车门与周围环境不发生干涉的情况下高效获取前后极限点位置.
优化过程在dfa文件中利用ug_optimize实例化的部分代码如下:
(child) section_optimization:
{
Class, ug_optimize;
Optimizer_Controls, {0.001,0.001,5000,5};
Design_Variables, {{self:,Xo,-2,2},
{self:,Tf,1,1.5},…};
Constraints, {{Rel_dis_X:,
DisX_OPd:Upper},
{Rel_dis_Y:, DisY_OPd:
Upper},{θ:,80,Upper}};
Objective, {{Df-d:,target,1.8},
{Dd-h:,target,5}};
};
最后利用NX Open API和C,将优化模型的迭代过程写入整体的分缝线设计模块中.前后极限点的确定是一个多因素影响和反复评估与修正的过程.优化迭代可以有效避免设计师频繁的手工迭代,快速寻找到合理的前后极限点.
2.3 基于多阶段灵敏度分析的断面优化
本文断面优化问题是一个多参数的非线性问题,无论采用哪种方法,迭代步数和优化时间都会比较长,本文采用无灵敏度分析、单次灵敏度分析、多阶段灵敏度分析机制进行对照,常规优化方法极其耗时,表1中的对照实验1实际结果证实了这一点.如表1中对照实验1中,多阶段灵敏度分析迭代次数是352,相对于无灵敏度分析迭代次数4 563大大减少,同时两种方法优化目标的拟合偏差基本接近.
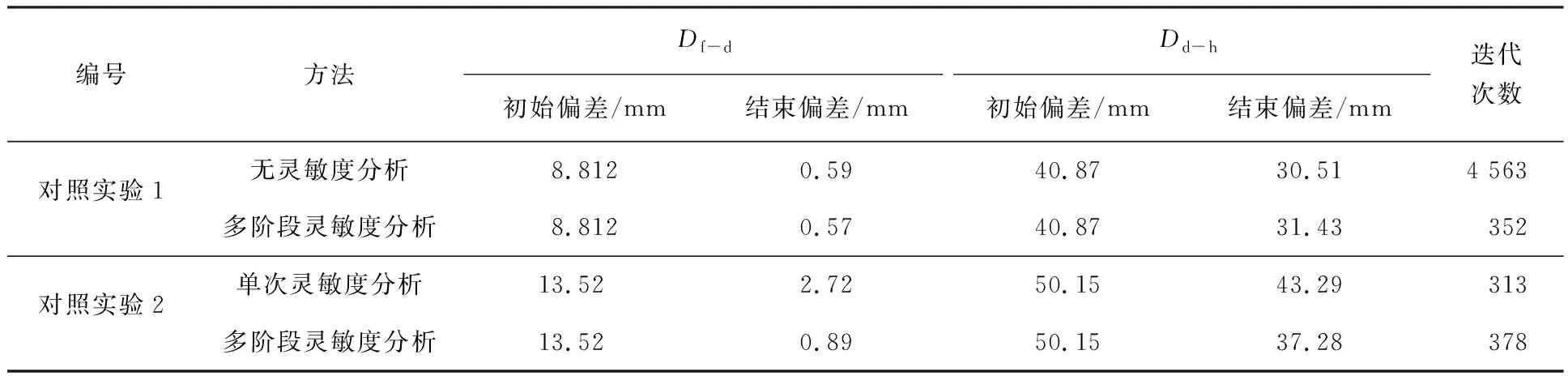
表1 不同优化机制对照
单次灵敏度分析优化机制基于单次的灵敏度分析的优化,初步排除了一些影响不大的设计变量,虽然明显提高了收敛速度,但由于排除了必要的设计参数,其收敛结果无法达到较高精度.如表1中对照实验2中,单次灵敏度分析过程中由于排除必要变量,仅优化部分灵敏变量,迭代次数为313,相比于常规优化大大提高,但是拟合偏差还是相对较高;而多阶段灵敏度分析在达到一次灵敏度值后再次对所有变量进行更新分析,挑选出灵敏变量再次进行优化,虽然迭代次数378较单次分析次数313高,但是优化目标的拟合偏差大大降低,如Df-d初始值为13.52,多次分析后降为0.89,降低率为93.42%;而单次分析后降为2.72,降低率为79.88%.多阶段灵敏度分析以相对较多迭代次数换取最后更低的拟合偏差,在一定意义上来讲是合理有效的,符合实际工程要求.
本文基于多阶段灵敏度分析优化机制有效地避免了这些问题,不仅收敛结果达到预期,并且优化步数相比于常规优化有较大优势,本研究中两组对照实验数据均基于模拟退火法,该方法对本类问题最为有效.本文数据通过设置多次不同初始偏差均得到以上结论,同时本文对其他优化方法比较,均获得相同结论.
2.4 极限点位置的缝合
本文基于多约束优化的方法自动高效求解出每个断面图上的前后极限点位置,每个断面设计模型上前后极限点位置显示分缝线的有效间隔.本文方法构造一系列通过铰链轴线和CAS的断面模型,获取所有断面模型上的极限点,为了保证K线的合理性和光顺性,本文通过使用B样条曲线[16]构造两条包络K线Line A和Line B,公式为
(1)
式中:C(u)为对应节点u在曲线上的点;U为节点向量集合,共有m+1个向量;k代表节点编号,u表示节点k与k+1的节点向量;Pi(i=0,1,…,n)为断面模型中优化获取的前极限点位置,共有n+1个;Ni,2(u)(i=0,1,…,n)为定义在节点向量集合U上的二次规范B样条基函数.
得到每个断面分缝线前后极限点位置后,利用NX Open API中CreateStudioSplineBuilderEx()将各个断面上的前极限点缝合成均匀合理二次样条曲线,从而得到均匀合理曲线的Line A.
对后极限点位置,使用同样的方法构造后极限K线Line B,保证分缝线恰好位于两条包络K线区域中,保证车门在转动时不会与车身结构发生干涉.
3 实例与分析
本文选取多个工程实例进行设计,首先在NX中进行初始数据设置,导入CAS、车门铰链等进行初始位置的布置,构造多约束参数化断面模型,通过构建一系列通过铰链轴线和CAS的多约束参数化断面模型进行优化.考虑到整体设计时间,本文合理选取模型的关键位置,如上下铰链的安装位置、车身宽度最宽处等16处位置.
然后,在工具开发模块Section Parameters模块中进行输入断面模型中的初始参数的最值并且自动访问断面模型Expressions中的铰链轴线、翼子板圆角中心、车门外板圆角中心位置参数,完成多约束参数化断面模型定义,如图8所示.
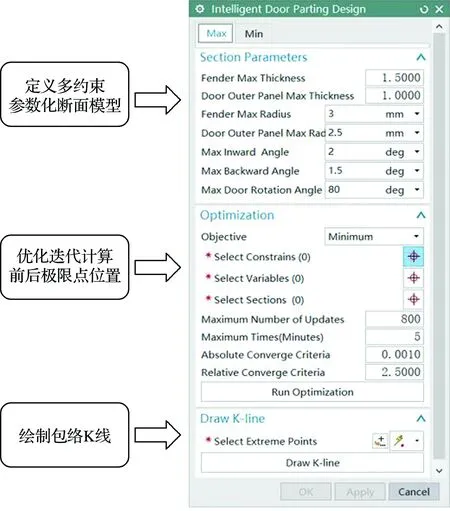
图8 车门分缝线开发工具
其次,在Optimization模块中定义优化条件,以分离点Pd作为初始迭代点完成优化得到不同断面模型上的前后极限点.
最后,在Draw K-line模块分别点选所有断面图上的前后极限点进行两条K线缝合.
本文方法能够求出有效K线,即可进行后续工程设计.以分缝线设计实例1为代表,优化得到车门与翼子板之间最小距离在下铰链中心断面处,为1.846 mm;在计算后极限点时,当车门开度最大80°时,车门与铰链之间的最小距离为16.709 mm,满足上文中理想值要求,如图9所示.
本文选取的大多数车身实例分缝线设计,只需在开发的软件模块中输入不同参数合理的优化域,并不需要进行结构调整,经过上述步骤可以得到合理光顺的K线Line A、Line B,如图10所示.
对于不能够绘制出合理分缝线的情况,如果分缝线始终位于K线区域之外,根据工程师的经验对CAS、B柱等进行微调,再次进行优化设计,如实例2中对车门内板铰链安装处局部凸起调整,如图11所示.

图9 实例1中最小间隙位置
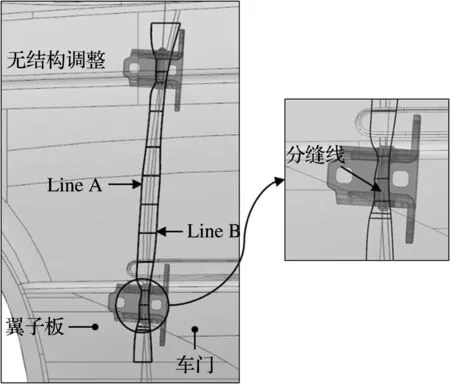
图10 车门分缝线设计实例1
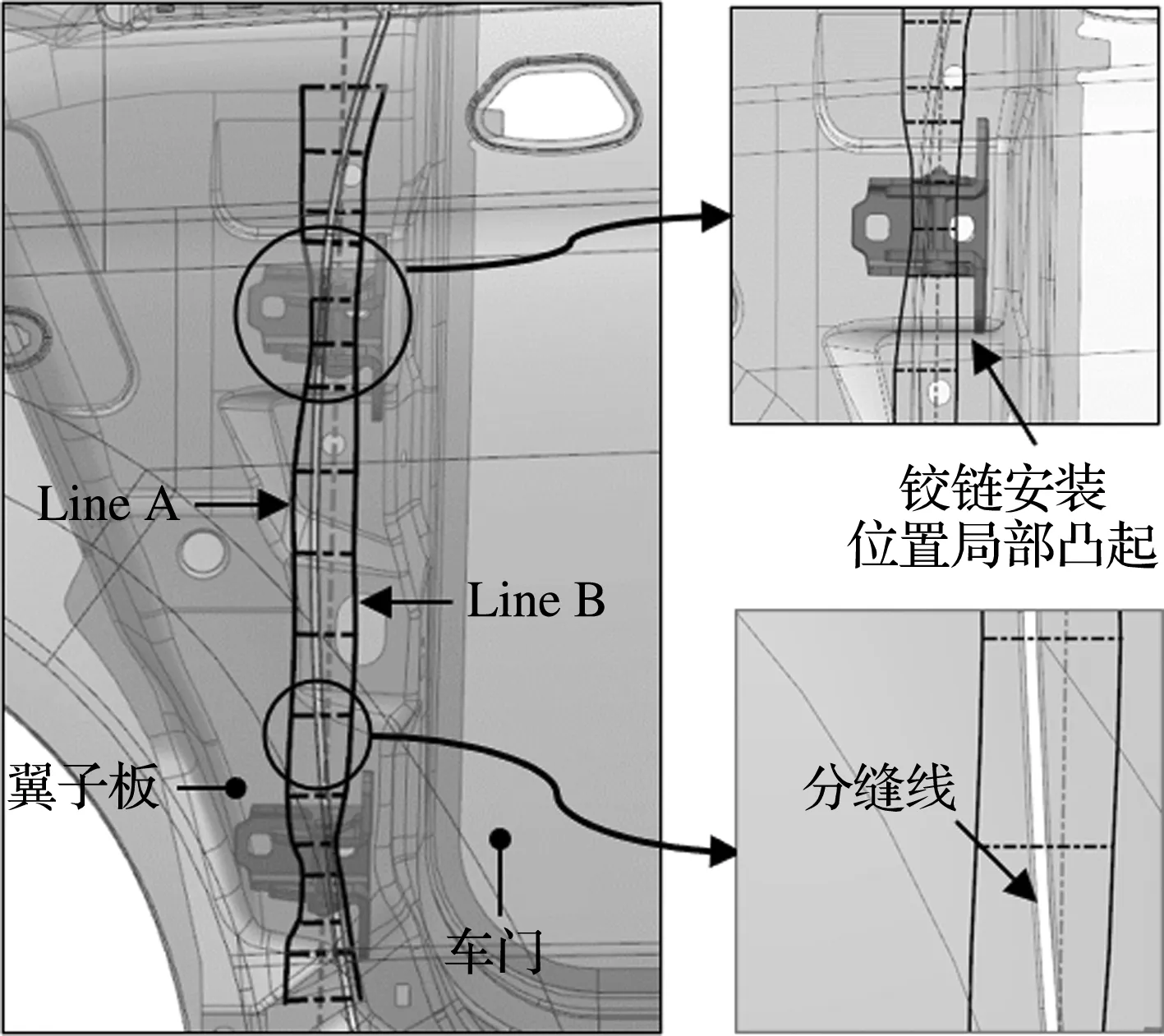
图11 车门分缝线设计实例2
通过以上分析,本文方法开发的车门分缝线模块不仅高效完成分缝线的设计并且考虑实际工程中的复杂约束,避免了手工迭代和常规二次开发的弊端.
手工设计方法可以准确地完成车门分缝线的设计,并且以设计师的经验和工程标准作为零部件设计的标准,但对于复杂车身零部件关联的结构,手工方法效率较低;常规二次开发的方法能够提高整体的设计效率,但是缺乏对复杂设计变量和附件间的复杂关联与工程约束的有效考虑.
本文综合考虑车身零部件设计过程中附件之间复杂的关联与约束以及自身结构中的工程规则、几何约束、设计意图,提高了对于复杂工程多约束问题设计的柔性、可靠性、合理性,与工程设计更加接近,如表2所示.

表2 不同方法的对比
4 结 语
多约束参数化断面模型避免了运动干涉分析,同时综合考虑车门分缝线正向设计中的多种复杂约束,通过高效的优化机制获取极限点位置,完成K线的缝合,并通过多个工程实例证明,实现了车门分缝线合理有效的自动化设计.
本文合理考虑了概念设计中的关联问题,将附件之间的内在关联以及零部件自身结构的多种工程约束和评价指标作为约束引入,以优化迭代的方法合理解决复杂工程问题.本文合理弥补了二次开发弊端,对复杂附件约束和关联有效描述.利用Measure Distance功能描述车门与附件的最小间隙,作为优化目标引入断面优化模型,避免了固有的运动干涉分析.本文有效解决了多约束与多评价指标的问题,综合考虑车门分缝线在实际设计中不同附件的工程设计参数、制造偏差、装配极限等约束,构建多约束参数化断面模型,不仅提高了解决问题的效率,并且拓展了解决问题的维度.
本文所提出的一整套流程与优化机制可以非常方便地移植于其他典型的CAD平台,对于车身复杂零部件设计是一种具有广泛参考意义的方法.

