气波引射前向流道波转子设计及性能研究

李 忠 辉， 赵 一 鸣， 纪 雅 文， 胡 大 鹏

( 大连理工大学 化工学院, 辽宁 大连 116024 )

0 引 言

天然气开采过程中，各气井地质储藏条件和开发程度不同导致井内压力存在差异[1-2].因此在集输压力固定[3]的情况下，为保证开采及输气稳定，工程中通常利用高压气井压力能对低压气井实现增压开采[4-5]，从而延长低压气井生命周期，提升能量及资源利用率.而气波引射技术作为一种新型压力交换方式[6-8]，凭借其转速低、结构简单、可带液运行、效率高等特点[9-10]，有望代替涡轮以及静态引射器，在增压开采领域得到广泛的应用.目前，胡大鹏等已针对直通道波转子气波引射机理进行大量研究，初步验证结构的可行性，并得到不同操作及结构参数对性能的影响规律[11-15].

通过对波转子内气体流动规律研究发现，引射过程中，直通道波转子流道壁面与气流之间存在明显相互作用力，导致进出口处产生旋涡和流动分离现象[16-18]，对设备性能带来不利影响.因此本文提出一种前向流道波转子结构，通过理论分析及数值计算确定流道形式、转子转速、气流运动之间的匹配关系，得到流道最优倾角的设计方法，最后进行实验确定不同工况下前向流道波转子引射性能变化规律，并与直通道波转子实验数据对比，证明结构的合理性.

1 前向流道波转子引射理论及倾角设计

1.1 前向流道波转子理想波图构建

为实现气波引射增压，波转子内需形成合理运动波系[19-21]，依据气体动力学原理和直通道波转子设计经验，将转子三维运动转化为流道二维平动，得到如图1所示的前向流道波转子理想波图.其中流道通过与各压力端口的接通、闭合产生压缩波C1、C2、C3和膨胀波E1、E2、E3并周期性重复此过程，从而实现高压气体对低压气体的气波引射增压过程.

1.2 前向流道倾角设计

根据波转子内气流运动规律，气体轴向射入后，由于压力波作用而逐渐加速，因此为使其与匀速转动转子间相互作用力最小，流道形式应采用后弯式，且后弯倾角沿轴向逐渐增大，进而形成一种前向流道结构.基于上述分析，综合考虑设计加工难度和对性能的影响程度，确定将进出口倾角θi和θo作为核心参数，其定义为相应位置流道切线与端面所夹锐角值.基于控制变量思想，忽略中间段倾角变化带来的影响，统一采用圆弧形式过渡，得到前向流道倾角理想匹配关系如图2所示，其中LP、HP、MP分别为低压、高压气体进口和中压气体出口.

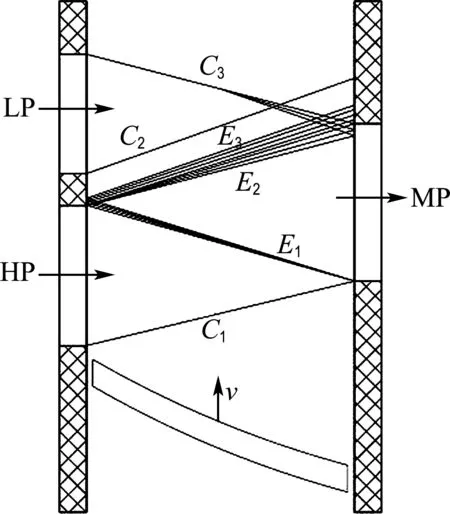
图1 气波引射波图

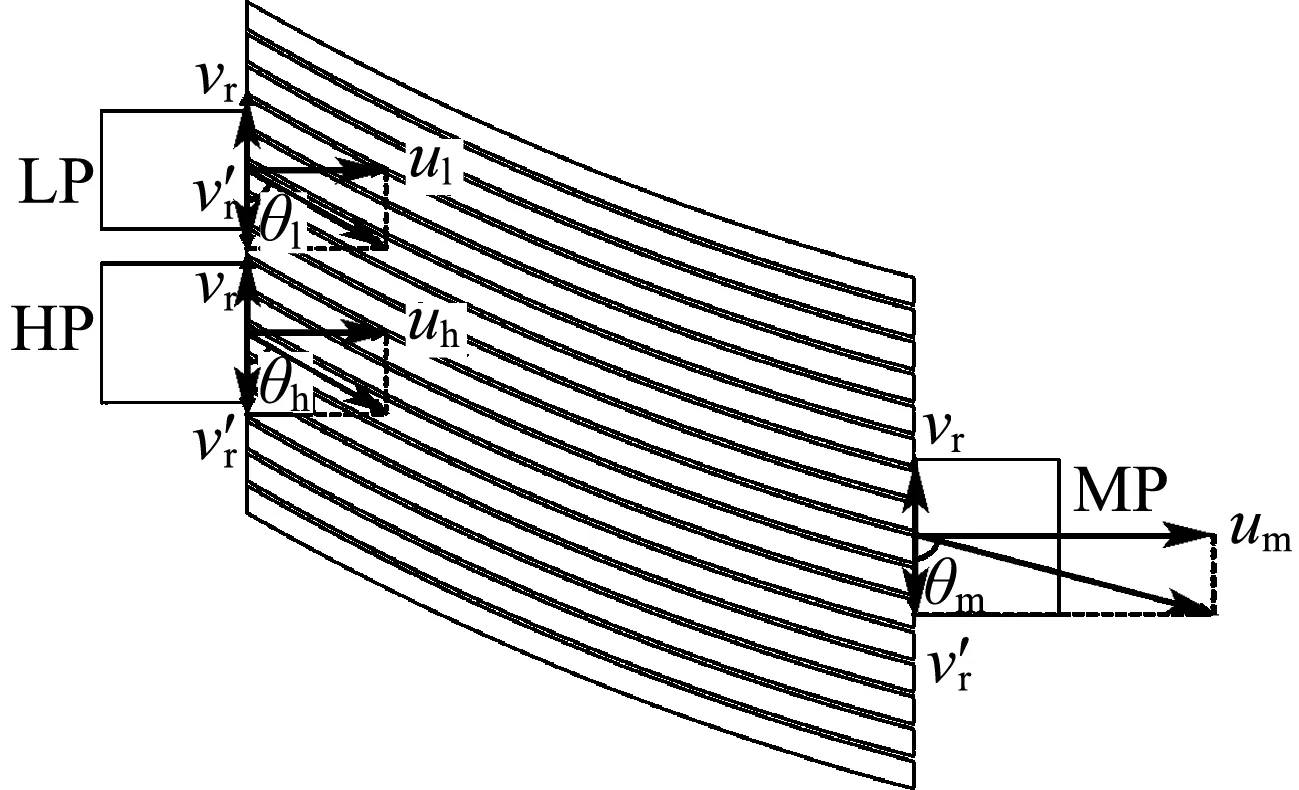
图2 倾角与转速最优匹配

流道与端口相对速度大小和转子转速相等，方向相反，其计算公式为

(1)

根据一维非定常等熵流动及简单波理论计算出气流轴向速度[22-23]，按图2所示矢量三角形，计算得到各端口附近流道最优倾角：

(2)

(3)

(4)

式中：ωr为转子角速度，rad/s；d为转子中径，m；vr为转子线速度，m/s；v′r为流道与端口相对速度，m/s；uh、um、ul为高、中、低压端口处气流轴向速度，m/s；θh、θm、θl为高、中、低压端口处最优倾角，rad.

按上述方法，针对表1所示工况及结构参数，计算得到高、中、低压端口最优倾角θh、θm、θl分别为57.9°、74.6°、63.9°.综合考虑设计加工难度，适当圆整后得到此工况下前向流道波转子进出口理论设计倾角θi和θo分别为60°和75°.

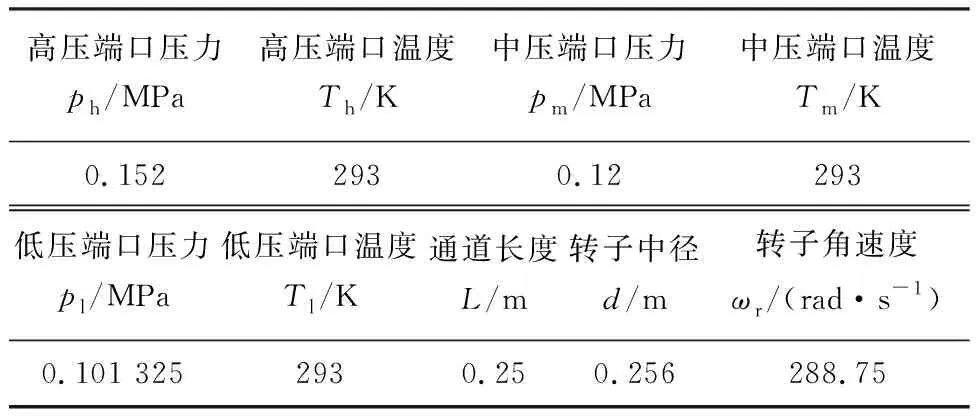
表1 气波引射器典型工况及结构参数

2 数值模拟及流场分析

2.1 计算模型及数值方法

依据理想波图，为直观研究气波引射过程中各端口及波转子内部气流运动状态，验证结构合理性，在综合考虑结果准确和计算效率的前提下，忽略密度较小介质所受离心力作用，如图3将转子三维转动转化为二维平动[24-25].利用Gambit软件进行网格划分，流道区域上下两侧设为周期性边界，端口、间隙及流道内部均采用结构化网格，全局尺寸为0.5 mm×0.5 mm，间隙及其附近网格进行局部加密，最终得到数值模型如图4所示.利用ANSYS Fluent软件进行瞬态计算，介质近似为理想空气；湍流计算采用RNGk-ε模型；选用AUSM+二阶迎风格式进行离散[26-28]，密度基隐式算法进行求解.

图3 三维向二维转换示意图

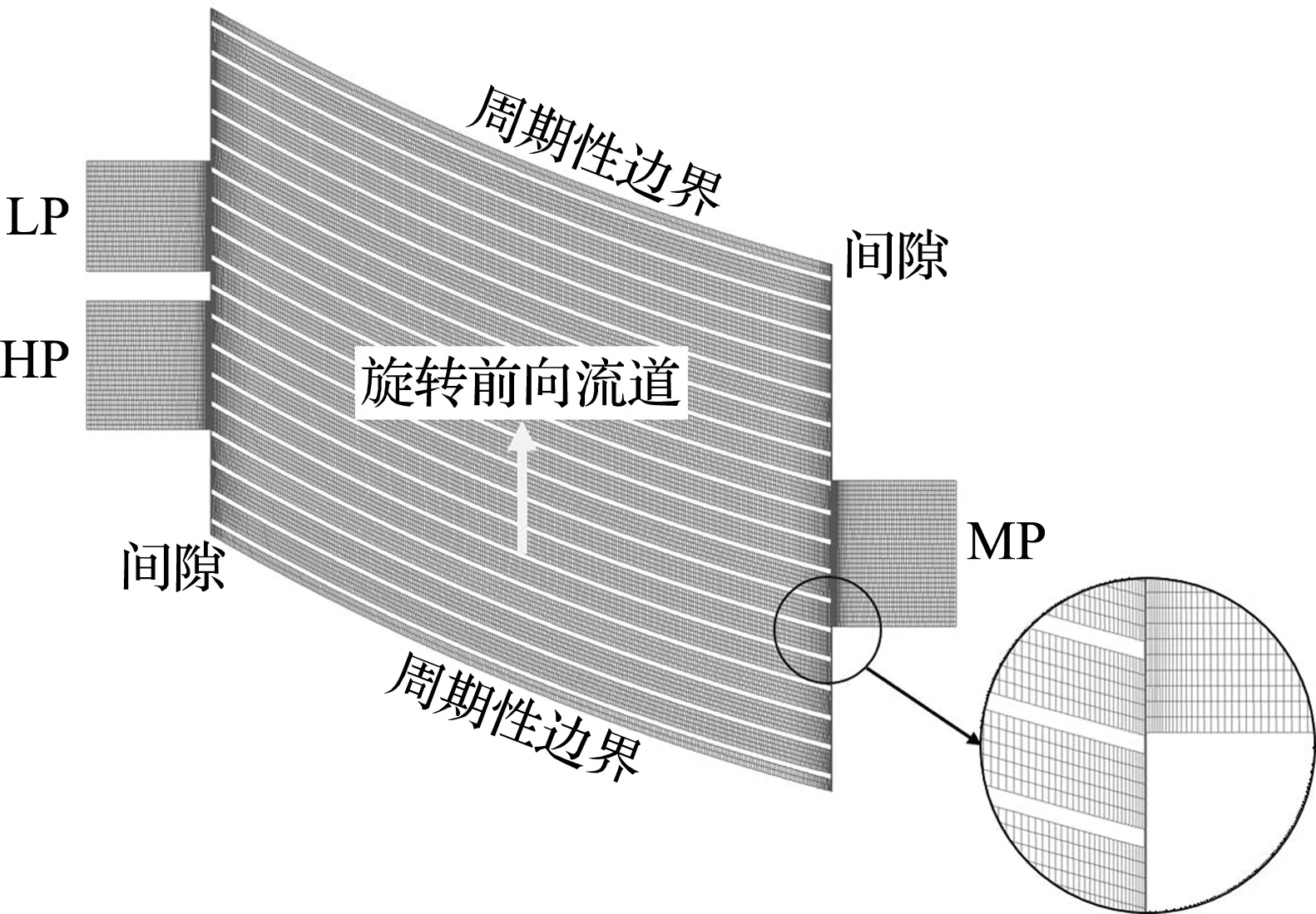
图4 二维网格模型示意图

基于Okamoto等的实验结果[29]，在相同工况及结构参数下基于上述数值方法得到流道内静压波动曲线与实验数据对比如图5所示.分析发现虽然由于忽略壁面传热以及粗糙度等因素导致模拟与实验存在细微偏差，但整体压力波变化规律与实验基本吻合，说明本文采用的数值模型可用于预测波转子内部气流运动情况，误差处于可接受范围.

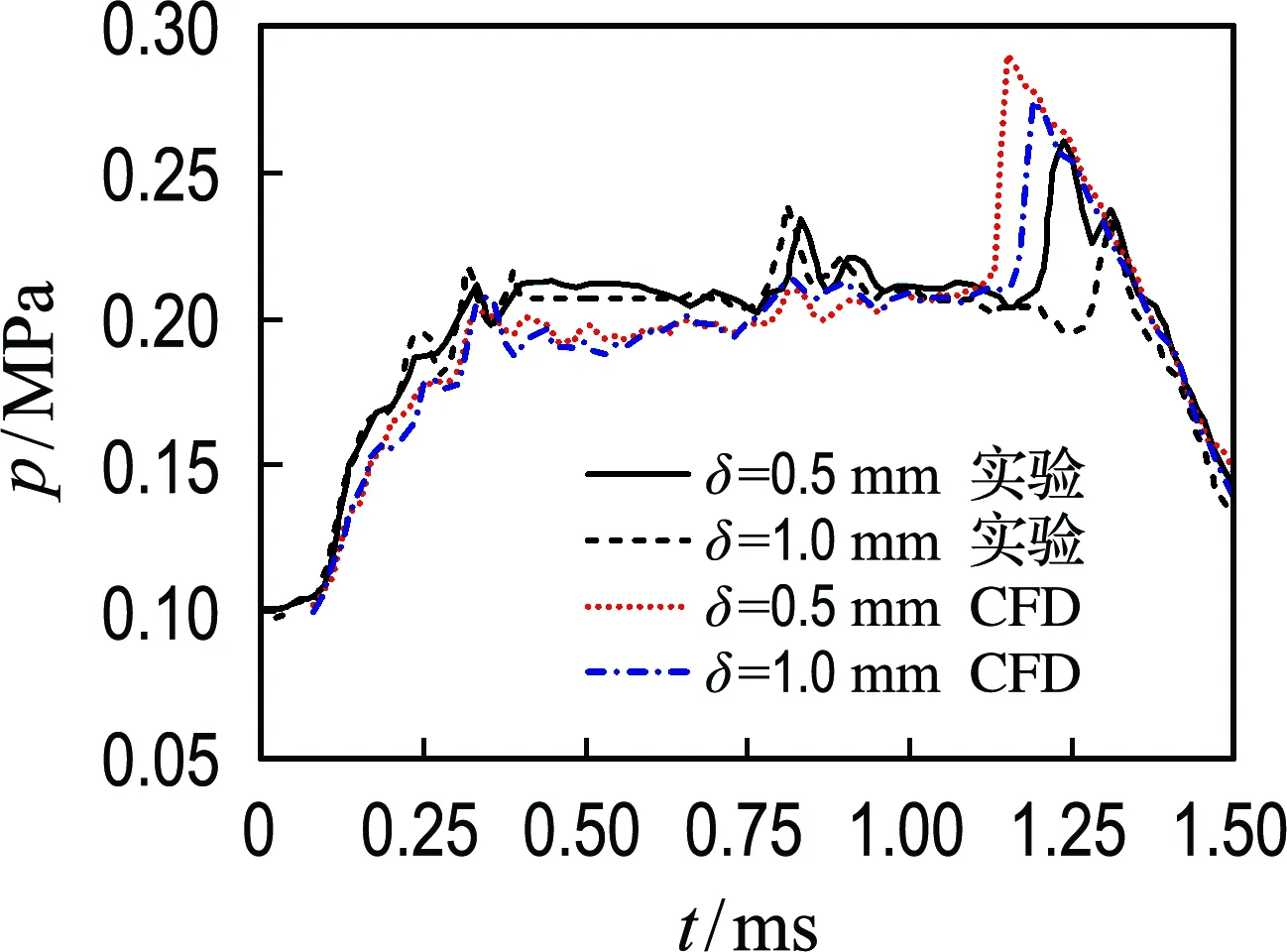
图5 模拟与实验静压值

2.2 不同倾角波转子性能及流场分析

按照上述数值模型，在表1所示工况下，对表2中不同倾角组合的前向流道波转子进行数值分析，得到其引射率和等熵效率如图6所示.

引射率和等熵效率计算公式如下：

(5)

(6)

式中：ξ为引射率；η为等熵效率；mh、ml为高、低压端口处气体质量流量，kg/s；Th、Tl为高、低压端口处气体滞止温度，K；ph、pm、pl为高、中、低压端口处滞止压力，Pa；k为绝热指数.

表2 波转子流道倾角组合

图6 不同倾角组合波转子性能参数

分析图6数据可知，针对表1工况，进口倾角θi为60°、出口倾角θo为75°的波转子引射率和等熵效率最高，与理论设计过程吻合.进一步对比分析各波转子内部流场如图7所示，其中图7(a)为直通道波转子流线图，此时入射气体由于受壁面施加的作用力而产生与通道运动方向相同的牵连速度，从而在进出口处产生明显旋涡和流动分离现象；而图7(b)中所示的60°/75°倾角组合波转子由于经过合理的设计，上述现象明显减少.图7(c)和(d)代表两种偏离最优设计点的前向流道结构，针对图7(c)，在进口倾角不变的条件下，增大出口倾角，发现进气侧流线基本与图7(b)一致，但出口侧气流由于受到壁面的作用，可明显观察到与直通道相同的流动分离现象；图7(d)是在出口倾角不变条件下减小进口倾角，从流线图中可看出进气侧由于匹配不合理导致流道上壁面对气流运动产生抑制，造成能量损失，进而影响出口处的匹配关系，产生轻微的流动分离.

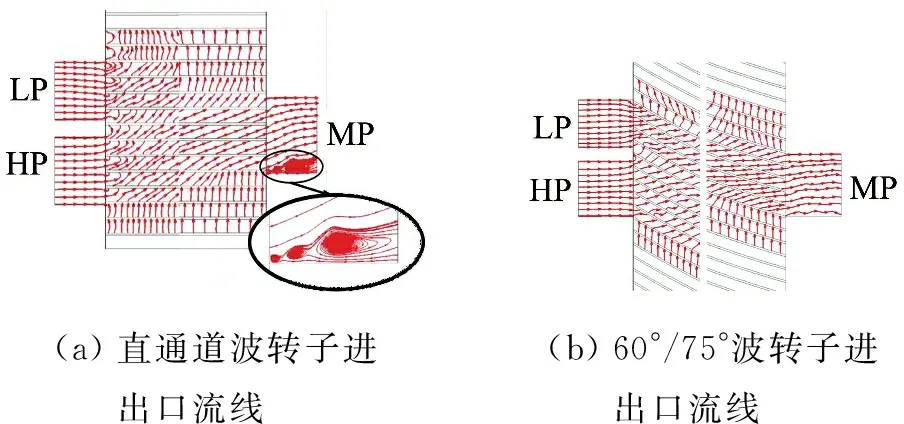
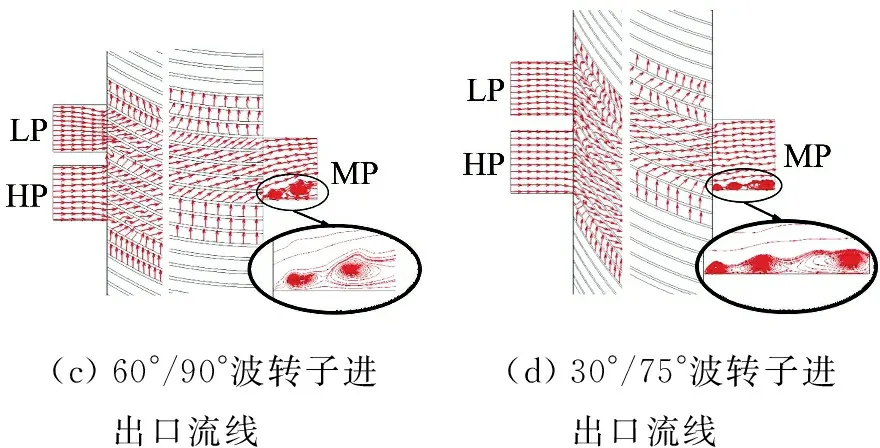
图7 不同倾角组合转子进出口流线图

综上，针对表1所示工况，进出口倾角θi和θo分别为60°和75°的前向流道波转子可有效减少转子与气流间相互作用力，避免旋涡和流动分离等影响设备性能的现象产生，从而提升引射性能，证明前向流道倾角理论设计方法的正确性.

3 性能实验及影响因素分析

基于理论设计及数值模拟结果，为与直通道波转子实验数据进行对比，参照文献[12]所用直通道波转子整体尺寸设计前向流道波转子，仅将流道形式改为进口倾角θi为60°、出口倾角θo为75°的前向流道，得到转子内部实物如图8所示.搭建如图9所示引射性能测试平台，实验中，高压气体由压缩机提供，并经过集气罐C1和稳压罐C2保证气流稳定，阀V3和V4可分别调节高压和中压端口压力，低压气源为大气，采用压力表、温度传感器和风速仪等设备测量各端口压力、温度以及气体流速，进而计算得到不同压缩比α和膨胀比β下设备引射性能.

(7)

(8)

图8 前向流道波转子结构实物图

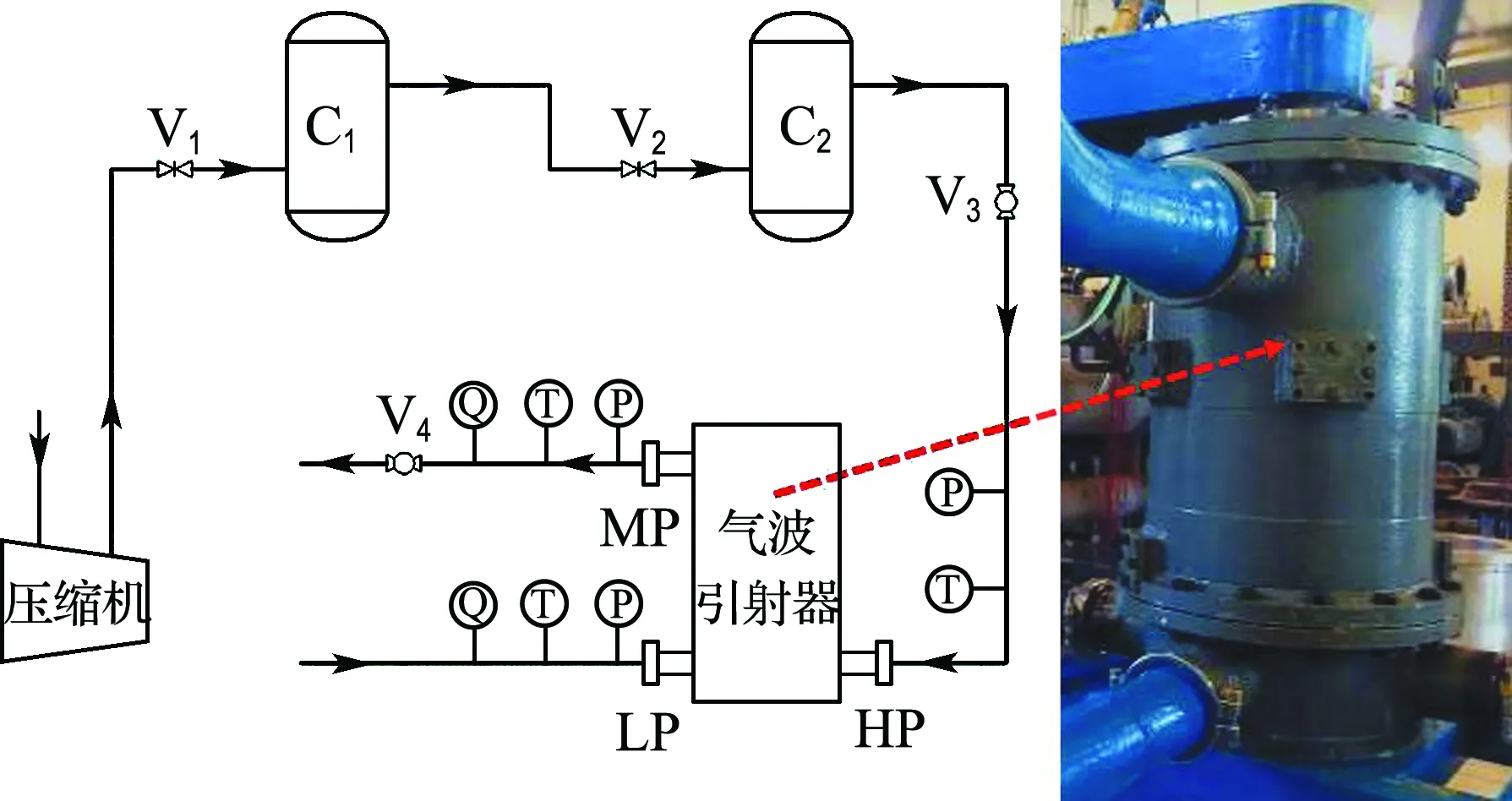
图9 气波引射实验流程图

采用控制变量方法研究压缩比α和膨胀比β对前向流道波转子引射性能的影响规律，实验中转速恒定为288.75 rad/s，通过调节喷嘴位置保证不同工况下波系最优匹配.

首先控制高压端口压力为0.152 MPa，调节中压端口压力，得到固定膨胀比条件下，不同压缩比前向流道波转子引射性能实验数据，并与直通道波转子实验数据对比如图10所示.分析图10中引射率和等熵效率柱状图可看出，当压缩比较小时，由于转子内气体流速较高，反向膨胀波E1较强，因此流道内低压区真空度较高，获得较高引射率，但此时流动损失增大，导致整体等熵效率较低；当压缩比较大时，中压端口附近可产生反向压缩波，影响波系匹配，导致引射率和等熵效率下降.因此，在膨胀比恒定条件下，随压缩比升高，前向流道波转子引射率逐渐降低，等熵效率先升高后降低，但均优于直通道波转子.分析前向流道波转子和直通道波转子引射率及等熵效率差值曲线发现，虽然其整体变化规律基本与对应性能参数变化规律一致，但在压缩比为1.20流道倾角设计工况点，由于转子结构和气流运动间形成最优匹配，导致性能提升幅度明显高于整体趋势.

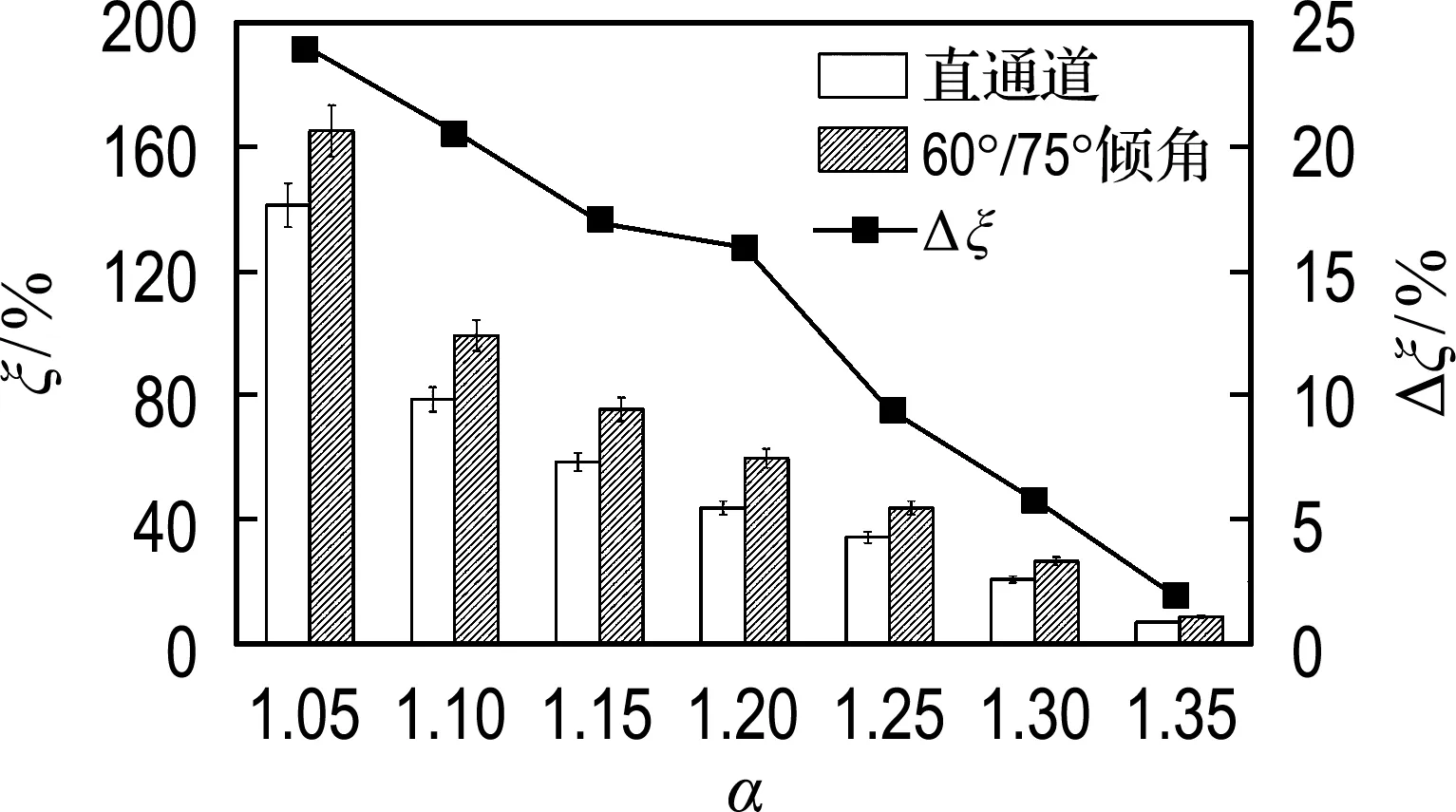
(a) 引射率

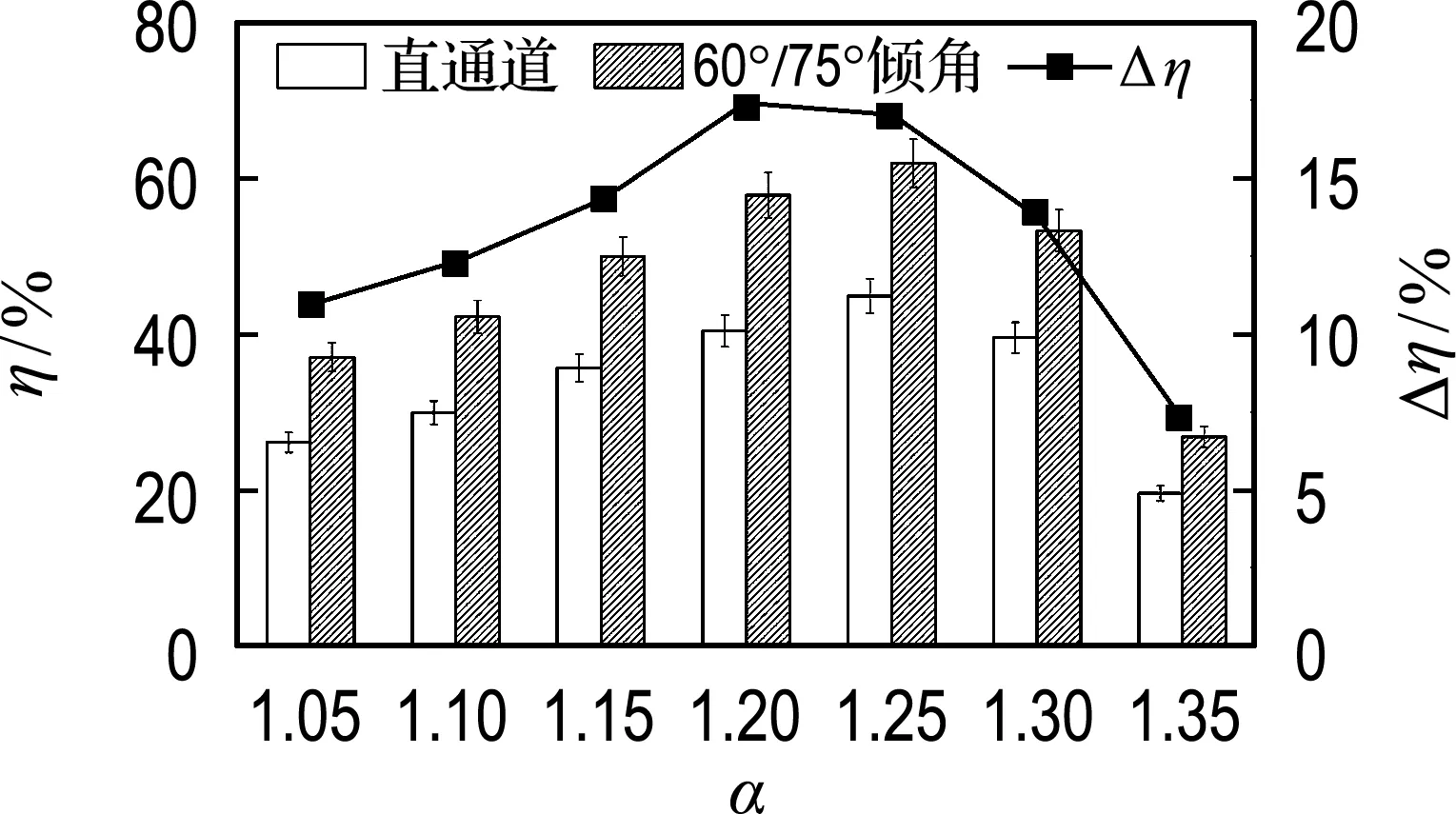
(b) 等熵效率

控制中压端口压力为0.12 MPa，调节高压端口压力，可得到固定压缩比下不同膨胀比前向流道波转子引射性能数据，与直通道波转子实验数据对比结果如图11所示.通过引射率和等熵效率柱状图可看出，小膨胀比时，高压和中压端口压差较小，反向膨胀波E1强度较弱，甚至产生反向压缩波，导致流道与低压端口接通时真空度较低，引射性能恶化；而大膨胀比下，气体流速升高，流动损失增加.因此，在固定压缩比下，随膨胀比升高，前向流道波转子的引射率和等熵效率呈现先上升后下降趋势，但均优于直通道波转子.分析前向流道波转子与直通道波转子性能差值曲线发现，其整体变化规律与对应参数趋势一致，且提升幅度最大点均出现在膨胀比为1.50的设计工况附近.

综上，与直通道波转子相比，前向流道结构可有效减少气体流动损失，提升引射性能，并在倾角设计工况附近提升幅度最大，引射率和等熵效率增幅比例均达到40%，证明此结构的合理性以及倾角设计方法的正确性.

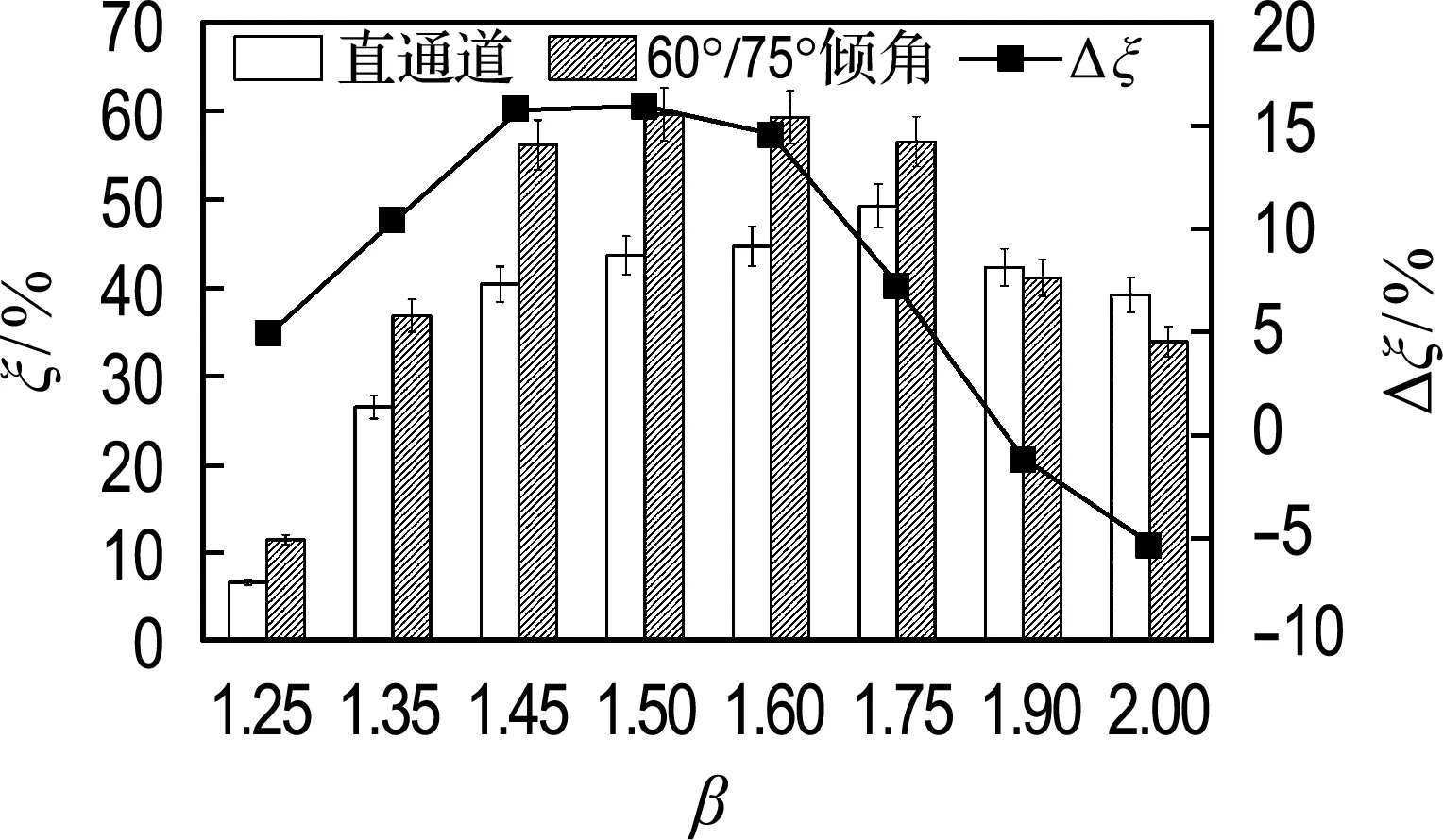
(a) 引射率

(b) 等熵效率

4 结 论

(1)当流道进出口倾角正切值等于气体流速与转子转动线速度比值时，气流与壁面间相互作用力减小，流道形式、气流运动、转子转速三者匹配关系优化，从而有效减少各端口以及流道中流动分离和旋涡现象，降低流动损失.

(2)针对前向流道波转子，当膨胀比固定不变，随压缩比升高，引射率呈现下降趋势，等熵效率先升高后下降；反之，当压缩比固定不变，随膨胀比逐渐升高，引射率和等熵效率均呈现先升高后下降趋势.

(3)与直通道波转子相比，在相同实验条件下，前向流道波转子引射率和等熵效率有明显提升，证明此结构的合理性，并且在倾角设计工况附近设备性能提升幅度达到峰值，引射率和等熵效率增幅比例均达到40%，进而验证了理论设计方法的正确性.