基于支持向量回归的定性-定量因子混合建模方法
冯 翔 宇, 石 茂 林, 马 跃, 宋 学 官, 孙 伟, 田 腾
( 大连理工大学 机械工程学院, 辽宁 大连 116024 )
0 引 言
数据建模是实现数据分析的基础,是完成工程系统设计、分析及优化的重要前提.在众多的数据建模方法中,支持向量回归(support vector regression,SVR)是具有代表性的一种,具有鲁棒性好、泛化学习能力强等优点[1-2],因此在计算机数值仿真及工程设计中得到广泛应用.例如,Lute等[3]通过支持向量回归建立了桥梁设计参数与最大应力应变的映射关系,实现了斜拉桥设计主梁和塔柱的应力应变预测;Edwin Raja Dhas等[4]基于支持向量回归建立焊接电学参数与焊接后部件残余应力相关关系,用于焊接过程的参数分析;Rahman等[5]基于汽车悬架臂的荷载和材料数据,采用支持向量回归预测悬架臂最大位移量及最大主应力;Lostado等[6]利用支持向量回归刻画了轴承预紧力、荷载和位移与车轴表面接触压力之间的关联关系.钱骥等[7]基于支持向量回归建立钢绞线应力预测的数学模型,并用于大跨度桥梁的检测监测;滕军等[8]以结构的动力和静力响应数据作为输入,多个设计参数作为输出,使用支持向量回归构建二者间的映射关系,实现了有限元模型多个参数的修正;狄勤丰等[9]基于有限元模型获得了套管部件的应力数据,通过支持向量回归建立了最大等效应力的预测模型.由以上工作可以看出,支持向量回归在预测、优化及分析等工程问题中均取得了成功应用.然而,以上研究中输入参数均为定量参数,而定量参数与定性参数并存的现象在工程实际中普遍存在[10].例如,机械零件尺寸设计参数可做定量改变,相应材料只能定性选择,设计出的零件应力应变等特性受尺寸定量参数与材料定性参数的共同影响[11-12].由于既有建模方法多基于输入参数间的空间距离描述彼此之间的相关关系,只能实现定量参数的数据建模,以至于既有方法不适用于描述定性参数间的相关关系.因此如何实现定量参数与定性参数的有效建模成为亟待解决的工程问题.
针对定量参数与定性参数混合建模问题,已经有很多学者提出了解决方案,并将定量参数及定性参数统称为定量因子(quantitative factors)和定性因子(qualitative factors)[13].其中具有代表性的是基于高斯过程的定性-定量因子建模方法.Qian等[14]建立了高斯过程模型中定性因子相关结构的一般框架,该框架采用半定规划估计法,保证了相关结构的正定性.Zhou等[15]在Qian等的高斯过程模型基础上,引入了超球参数化对定性因子之间的关系进行建模,量化了定性因子之间的关系.Deng等[16]进一步改进了定性因子之间的相关结构,提出了更灵活的加性高斯过程模型,并通过数值及工程案例证明了所提方法具有更好的预测性能.然而,以上定性-定量因子混合建模方法基于高斯过程,需要对相关性矩阵进行求逆运算,要求训练样本的均布性较高,以保证求解的稳定性,且存在模型易过拟合等弊端[17].支持向量回归可通过将训练数据设置为支持向量及非支持向量提升模型泛化能力,并通过正则化系数控制拟合程度,而其相应的定性-定量因子混合建模方法还未见报道.为此,本文提出一种定性-定量因子支持向量回归算法解决定性-定量因子混合的问题.在该算法中,构建一种新型核函数描述定性-定量因子间的耦合关系,利用优化核函数超参数获取最优模型.本文采用多个数值案例验证所提方法的有效性,核验数个经典工程问题,并通过种植牙中种植体骨应力预测的应用,检验该算法解决实际工程问题的能力.
1 算法介绍
1.1 支持向量回归
支持向量回归源于支持向量机(SVM),其通过在高维空间构建最优超平面来拟合样本,对于一组数据集{(x1,y1),(x2,y2),…,(xm,ym)},有
yi=wTφ(xi)+b;i=1,2,…,m
(1)
其中w=(w1w2…wm)是权重矢量,b是偏置项,φ(x)为低维空间到高维空间的映射函数.在实际的预测问题中,数据很难满足式(1)中所示回归方程.为此,研究人员对于式(1)进行改进,设定模型输出和真实输出之间最多有≥0的偏差,记为不敏感损失参数.为了得到最大间隔的划分超平面,优化参数w和b,求解如下公式:
(2)

s.t.yi-(wTφ(xi)+b)≤+ξi
(wTφ(xi)+b)-yi≤+ξi

(3)

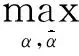


(4)
偏置项b为
(5)
通过核函数R(x,xi)表示数据映射关系φ(x),则支持向量回归的最终表达形式为
(6)
1.2 定性-定量因子支持向量回归
记输入数据中有p个定量因子x=(x1x2…xp)T和q个定性因子z=(z1z2…zq)T,且对于第j个定性因子zj有mj个等级.
对于定量因子输入数据建模,支持向量回归的核函数映射关系为
φ(·)=σ2R(·|θ)
(7)
其中σ2是方差参数,R(·|θ)是由核函数参数向量θ=(θ1θ2…θp)T确定的核函数.对任意两组具有相同维度的定量因子输入量xi=(xi1xi2…xip)T和xj=(xj1xj2…xjp)T,核函数表述如下:
(8)
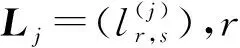
(9)

结合式(8)所示定量因子高斯核函数和式(9)所示定性因子相关性矩阵,选用一种核函数组成结构,用于分析定量因子映射关系和定性因子相关性之间的组合形式[16].此核函数组成结构的映射关系如下所示:
(10)

为了使算法能更加精确地建立映射关系,本文引入灰狼优化算法(grey wolf optimizer,GWO)[19],用于提出算法的参数寻优.
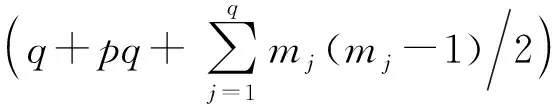
(11)

ψj,r,s∈(0,π)
σj≥0
(12)
除了核函数映射关系中的参数,支持向量回归的不敏感损失参数和正则化参数C也需要优化取得合适的数值[20].在算法模型的建立过程中,将以上需要优化的参数设置在同一个位置向量P中,并根据约束条件设置合适的寻优范围,超参数优化解都由灰狼优化算法经迭代求解得到.
本文提出的定性-定量因子支持向量回归(quantitative-qualitative factors support vector regression,QQ-SVR)算法建立过程的伪代码如下:
输入:混合定性-定量因子的输入数据(x,z);输出数据y
输出:QQ-SVR模型
1: 设置GWO的种群规模数A、最大迭代次数Imax、误差阈值Rmin;设置迭代次数的初始值I←1;
2: 设置待优化超参数向量P的初始值及优化区间;
3: whileR 4: GWO调整P中超参数位置; 5: 将(x,z)和P代入式(10),得到核函数映射φ; 6: 将φ和y代入式(4)~(6),构建QQ-SVR临时模型; 7: 将(x,z)代入QQ-SVR临时模型,计算预测结果; 8: 计算预测结果与y之间的误差R; 9: 迭代次数I←I+1; 10: end 11: return最终的QQ-SVR模型 本文通过多组测试函数验证提出的定性-定量因子支持向量回归(QQ-SVR)算法的预测性能,如表1所示.实验中,采用拉丁超立方抽样方法为定量因子输入采样,定性因子输入为全析因设计,其包含所有的等级组合.输入数据组合了定性因子和定量因子,并通过给定函数获取输出数据,生成训练样本与测试样本.在训练样本输出数据中添加区间为~U[-0.1,0.1]的白噪声.为检验算法对样本均布的依赖程度,设置测试函数(1)~(4)中训练样本的定量因子采样区间与测试样本不同.与此同时,选用来自UCI数据库的基准测试数据集对算法进行数值实验,其输入数据同时包含定性因子和定量因子,各数据集的基本信息如表2所示,训练样本和测试样本皆为随机抽取. 表1 测试函数数据集 表2 基准测试数据集 采用基于灰狼优化算法的支持向量回归(SVR)算法,文献[15-16]中的两种定性-定量因子高斯过程回归算法(UC和AD_UC),以及本文提出的QQ-SVR算法构建预测模型.设定SVR和QQ-SVR中用于参数寻优的GWO种群规模数为20,最大迭代次数为50,误差阈值为0.01.为了减少随机因素影响,每组数据集做30次独立分析,并以30次预测值的均方根误差(Erms)作为算法预测效果的评估指标,如下所示: (13) 计算并统计每次实验得到的均方根误差值,获得四分位箱线图如图1、2所示.可以看出,本文提出的算法相比于SVR、UC和AD_UC能够提供更好的预测结果,对各组测试样本预测的均方根误差的平均值有较为显著的降低,其数值统计结果如表3所示. (a) 测试函数(1) (b) 测试函数(2) (c) 测试函数(3) (d) 测试函数(4) (e) 测试函数(5) (f) 测试函数(6) (g) 测试函数(7) (h) 测试函数(8) (i) 测试函数(9) (j) 测试函数(10) (k) 测试函数(11) (l) 测试函数(12) (m) 测试函数(13) (n) 测试函数(14) (o) 测试函数(15) (p) 测试函数(16) (a) Servo (b) Yacht (c) Auto-MPG (d) ENB 表3 均方根误差平均值 为了统计性地比较本文提出算法与其他算法预测性能,采用t检验对各组测试函数所得结果进行检验,零假设及备择假设如表4所示.检验结果列于表5,可以看出大部分实验结果的t检验得到的p值小于0.05,拒绝零假设,即在多数情况下提出算法的预测误差显著低于对照算法.提出算法在面对不同种类的定性-定量因子混合输入的数据集时,都能获得较为理想的结果. 表4 t检验的零假设和备择假设 表5 t检验分析结果 通过以上数值实验的分析可以得知:与普通的支持向量回归算法相比,式(10)所示的核函数映射关系能有效地描述定性因子与定量因子之间的耦合关系.此外,因训练样本中存在白噪声,且测试函数(1)~(4)中训练样本的数据均布性较差,对相应数据集测试结果进行分析可以得知:与基于高斯过程回归的定性-定量因子算法(UC、AD_UC)相比,本文算法的支持向量回归结构使得它所构建的预测模型具有较好的鲁棒性和泛化性. 将算法应用于3例经典工程问题,分别为弹簧设计[21]、焊接梁设计[22]和压力容器设计[23].这些工程问题中,输入参数同时包含定性因子与定量因子,所以适用于检验算法对于此类工程问题的建模效果.实验中,定量因子由拉丁超立方抽样方法采样,定性因子采用包含所有组合情况的全析因设计,并通过工程函数生成训练样本和测试样本.分别使用基于灰狼优化算法的支持向量回归(SVR)算法、两种基于高斯过程回归的定性-定量因子算法(UC和AD_UC),以及本文提出的QQ-SVR算法建立相应的预测模型,其中算法的参数设置同2.1节所述. 该问题的目标是预测如图3所示的弹簧质量,它受3个变量影响:导线直径(d)、线圈直径(D)以及有效圈数(N),其中d和D是定量因子,而N是定性因子.实验设计如表6所示.各算法预测误差如表7所示,本文提出的算法预测精度最高. 图3 弹簧设计示意图 表6 弹簧设计实验设计 表7 弹簧设计实验预测均方根误差 该问题的目标是预测如图4所示的焊接梁成本,它受3个变量影响:焊缝厚度(h)、杆件附加部分长度(l)以及杆件的型号(P),其中h和l是定量因子,P只能被定性选取.实验设计如表8所示.各算法预测误差如表9所示,本文提出的算法预测精度最高. 图4 焊接梁设计示意图 表8 焊接梁设计实验设计 表9 焊接梁设计实验预测均方根误差 该问题的目标是预测如图5所示的压力容器总成本,它受4个变量影响:壳体厚度(Ts)、封头厚度(Th)、内径规格(R)以及圆柱长度规格(L),其中R和L是定量因子,而Ts和Th被设定为定性选取.实验设计如表10所示,各算法预测误差如表11所示,本文提出的算法预测精度最高. 图5 压力容器设计示意图 表10 压力容器设计实验设计 表11 压力容器设计实验预测均方根误差 通过此3个经典工程算例的实验结果可以得知:相较于其他算法,本文算法在解决受定性-定量因子混合影响的工程问题时,具有更强的建模能力,预测精度也更高.实验结果同时也表明,本文算法适用于解决工程问题,在工程实践的设计与应用中具备一定的参考价值. 将本文算法进一步应用于种植牙中种植体骨应力预测以检验其工程实践意义.如文献[24-25]所示,种植体骨应力在种植体的设计过程中是一个重要的参考指标,通常在设计过程中使用有限元分析生成数据集,再建立代理模型,通过少量采样点获取种植体结构及材料参数与骨应力在全部空间中的相关关系,实现对空间中任意一点骨应力的预测.种植体骨应力主要受种植体结构参数和材料类型的影响,其中结构参数可按设计需求做出改变,而材料类型则相对有限.然而现有的文献中,多数的代理模型忽略材料类型对种植体骨应力的影响,或将材料类型的选取简单等效成材料参数的数值变动,如Roy等[26]基于有限元分析的结果,仅针对种植牙尺寸参数建立骨应力优化的遗传算法模型;Kitagawa等[27]基于有限元分析的结果,将不同材料的皮质骨弹性模量作为输入,建立种植牙骨应力预测模型.这样的建模方式容易忽略材料类型变量中潜在的耦合关系,造成骨应力预测的结果不准确.因此,有必要在建立预测模型的过程中充分考虑两类变量的混合影响.在种植体骨应力分析中,尺寸参数可视为定量因子,材料类型可视为定性因子,在本节中,即通过本文提出的定性-定量因子支持向量回归(QQ-SVR)算法实现种植体骨应力预测. 构建由皮质骨、松质骨、种植体、牙冠、中央螺丝5部分组成的种植牙系统模型,如图6所示. 图6 种植牙系统模型剖面图 本文选取结构参数如下:种植体长度(Li)、螺纹长度(Ls)、螺纹螺距(P′)、等腰三角形种植体牙型底边长度(Lt)、底角角度(β),相应取值范围如表12所示.种植体和牙冠可选材料共有3种,具体参数及相应定性因子如表13所示,模型其余 部分的材料参数如表14所示. 表14 其余组成部分的材料参数 种植牙系统有限元网格划分如图7所示,其中种植体、牙冠、中央螺丝接触方式为Frictional,摩擦因数为0.3;种植体与骨组织接触、松质骨与皮质骨的接触类型均为Bonded.设置皮质骨的底面边界条件为全约束,侧面边界条件为无摩擦约束,在牙冠上加载竖直向下荷载150 N,中央螺丝预紧力加载150 N.经过有限元计算后得到的种植体骨应力云图如图8所示. 图7 种植牙系统有限元网格划分 图8 种植体骨应力云图 实验中,使用拉丁超立方抽样方法对种植体模型中的结构参数进行采样,种植体和牙冠的材料采用包含所有组合情况的全析因设计.将结构参数设定为定量因子,种植体和牙冠的材料类型编号设定为定性因子,结合成为输入数据.将相对应的有限元模型计算得到的种植体骨应力作为输出数据.实验一共得到50组输入和输出数据,随机选取40组作为训练样本,剩下10组作为测试样本.采用基于灰狼优化算法的支持向量回归(SVR)算法、两种基于高斯过程回归的定性-定量因子算法(UC和AD_UC)以及本文提出的QQ-SVR算法分别构建种植体骨应力预测模型,算法参数设置同2.1节所述.计算各模型对种植体骨应力的预测值与测试样本中真实值之间的均方根误差作为算法预测效果的评估指标.实验结果如表15所示. 表15 种植体骨应力预测均方根误差 从表中可以看出,本文提出的QQ-SVR算法相比对照算法可以显著提升种植体骨应力的预测精度.相较于SVR、UC和AD_UC,本文算法对种植体骨应力预测的均方根误差分别降低了43.8%、31.4%和68.6%.实验结果同时也再一次表明,此算法适用于工程实际中基于定性-定量因子混合输入的建模,具有一定的实用价值. 本文回顾了支持向量回归在计算机仿真和数值设计中的应用以及对定性-定量因子混合输入建模的研究现状,并针对现有算法对定性-定量因子难以有效建模的问题,提出了定性-定量因子支持向量回归算法.在该算法中,通过一种新型核函数描述定性-定量因子耦合关系,在此基础上给出了定性-定量因子支持向量回归推导及参数优化方法,实现了定性-定量因子混合数据的有效建模.多组计算机数值实验、经典工程算例分析以及种植体骨应力预测实验表明,所提算法相比较于现有的其他算法,对定性-定量因子混合输入的建模能力更好,能够提供更为准确的预测结果,并具有一定的工程实践能力.2 数值实验
2.1 实验设计

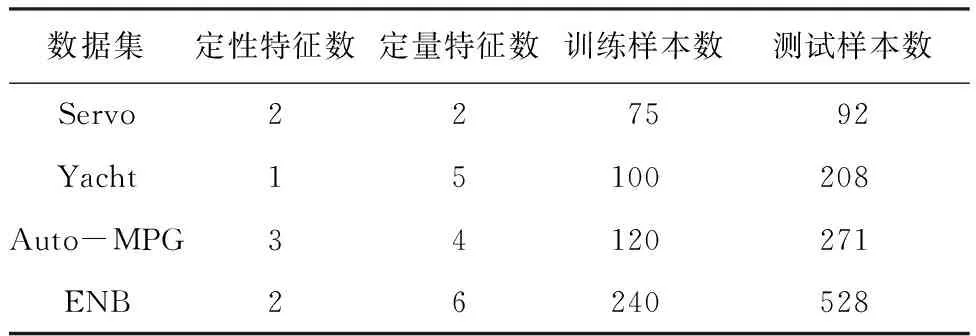

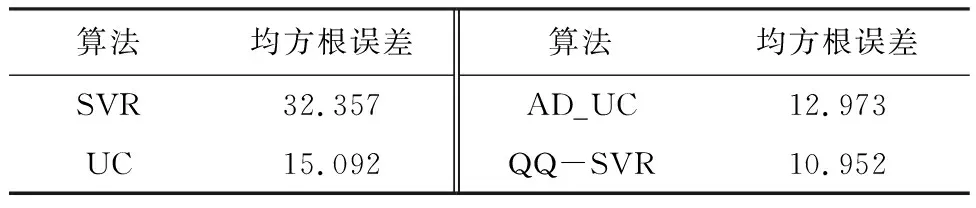
2.2 结果与讨论
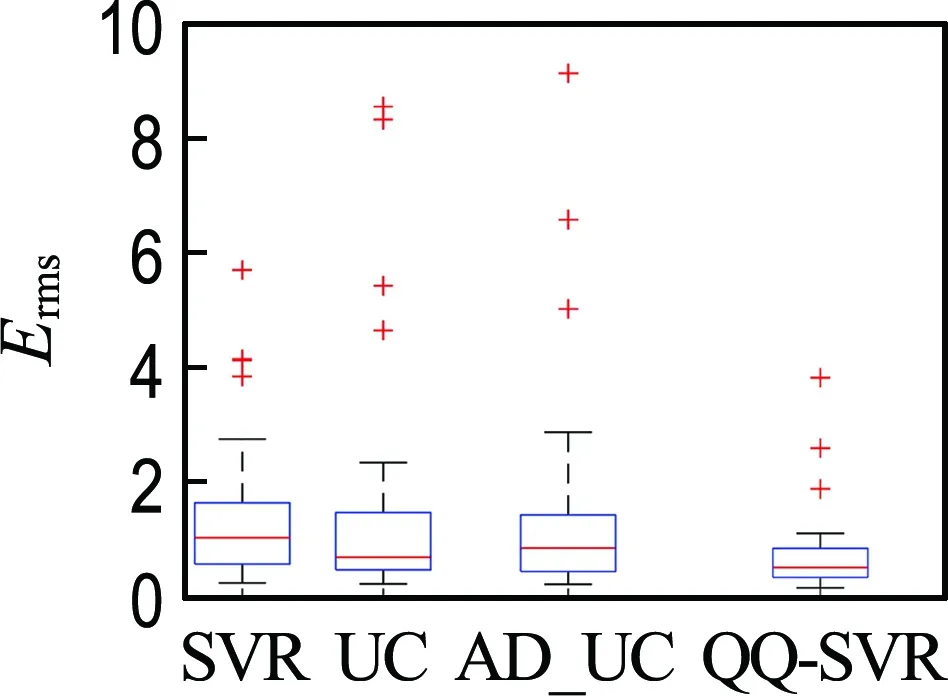

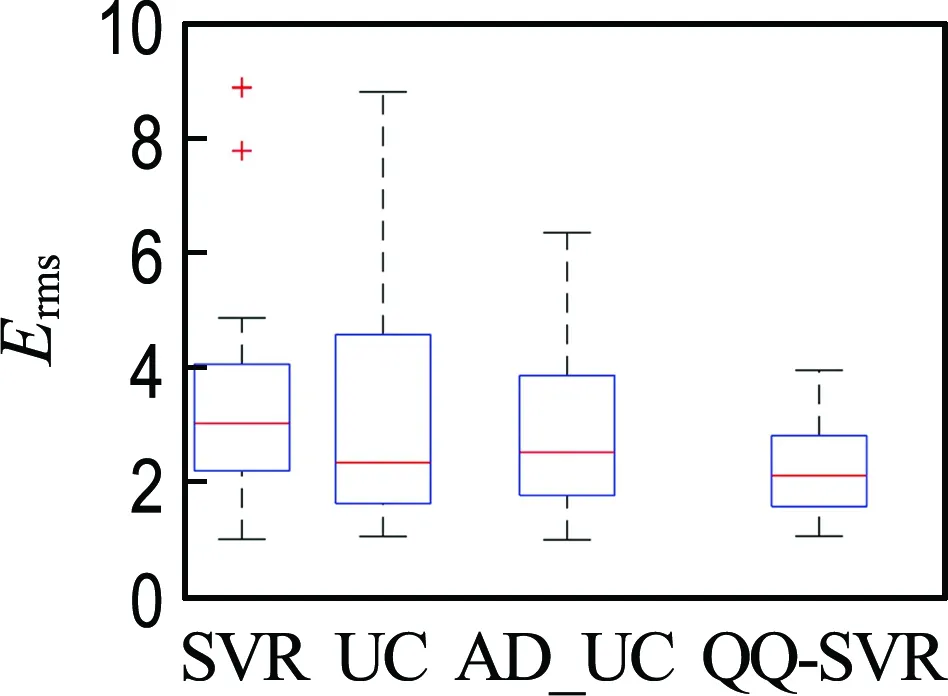
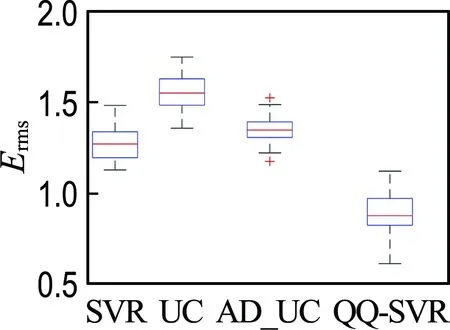



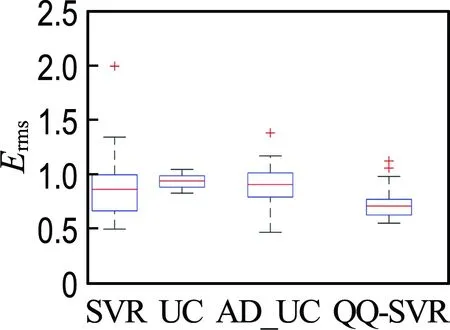
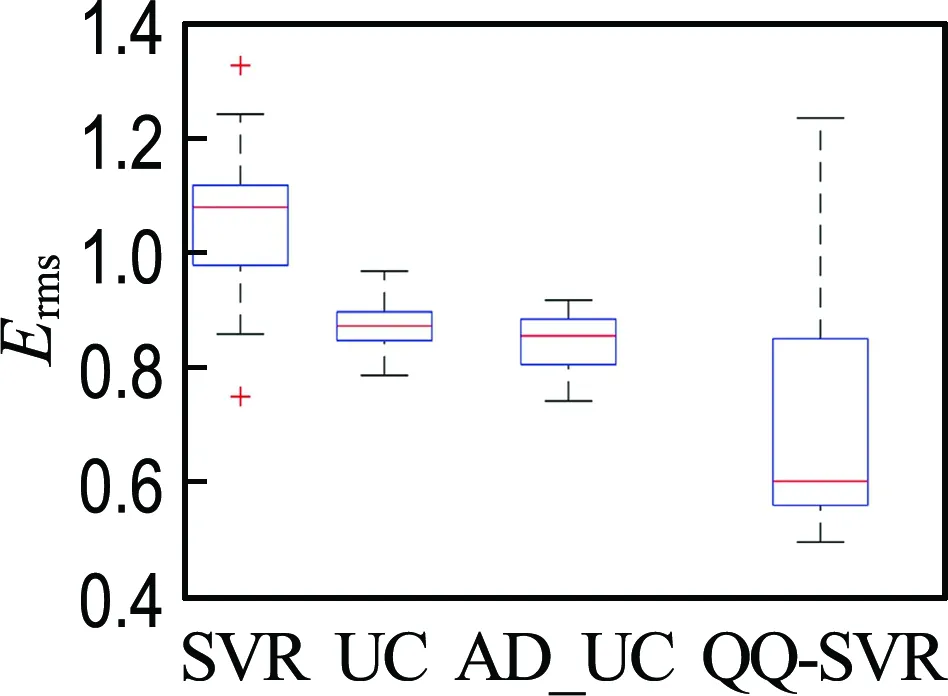


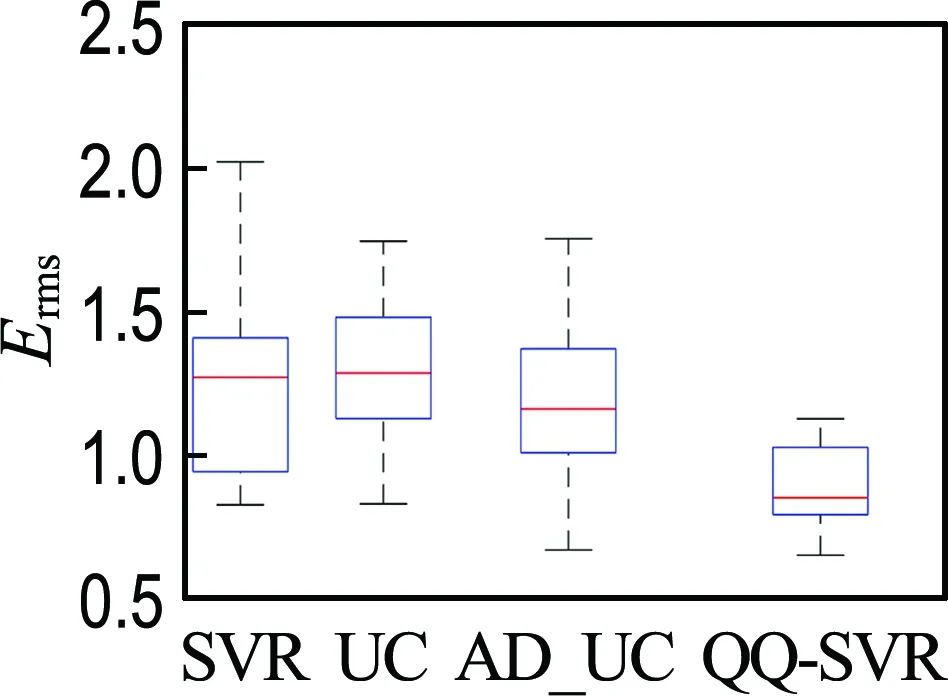
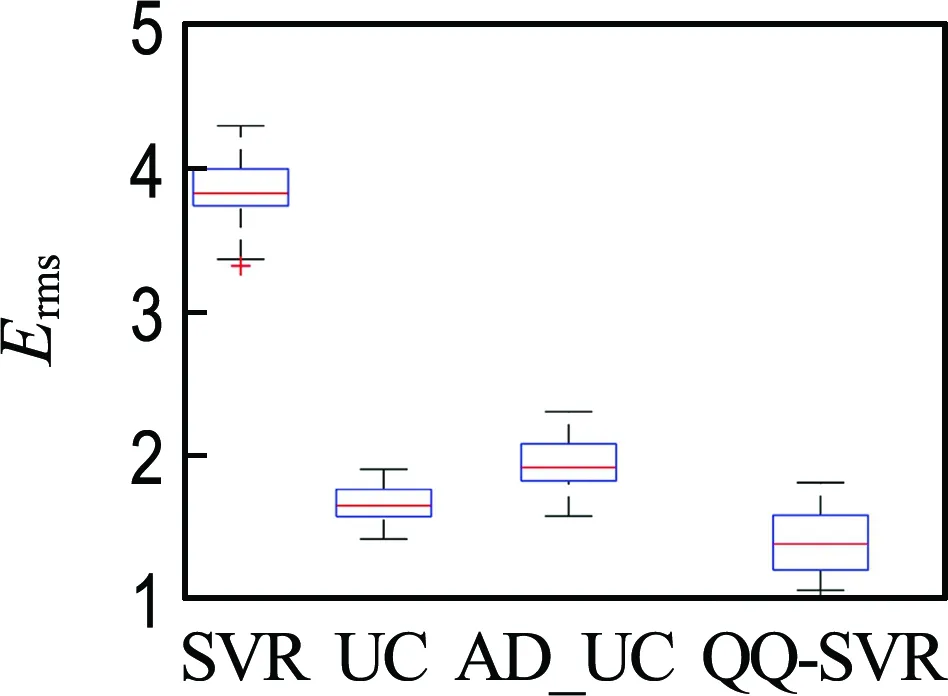



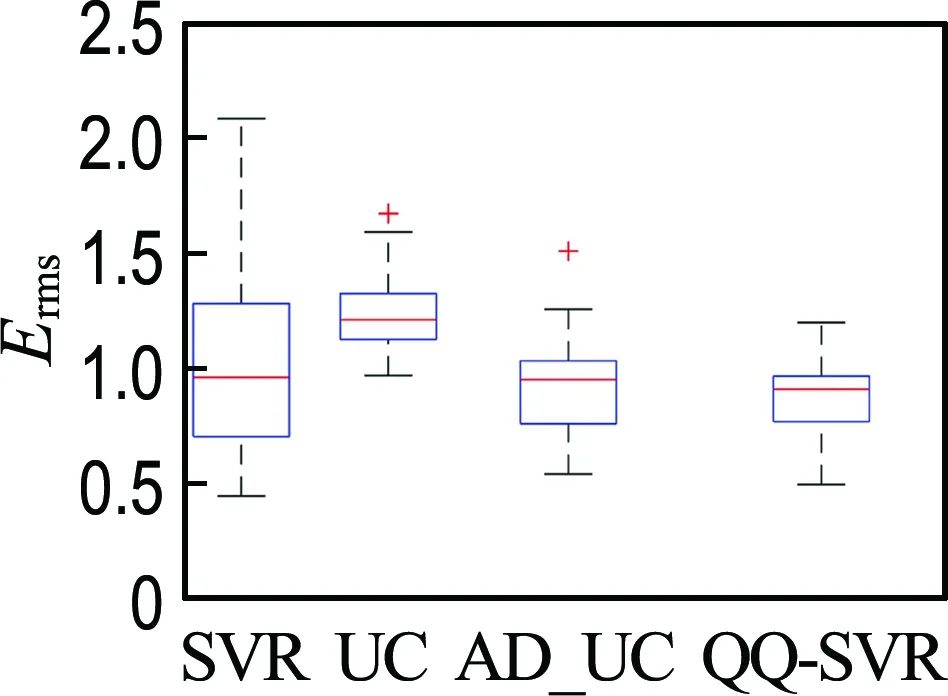
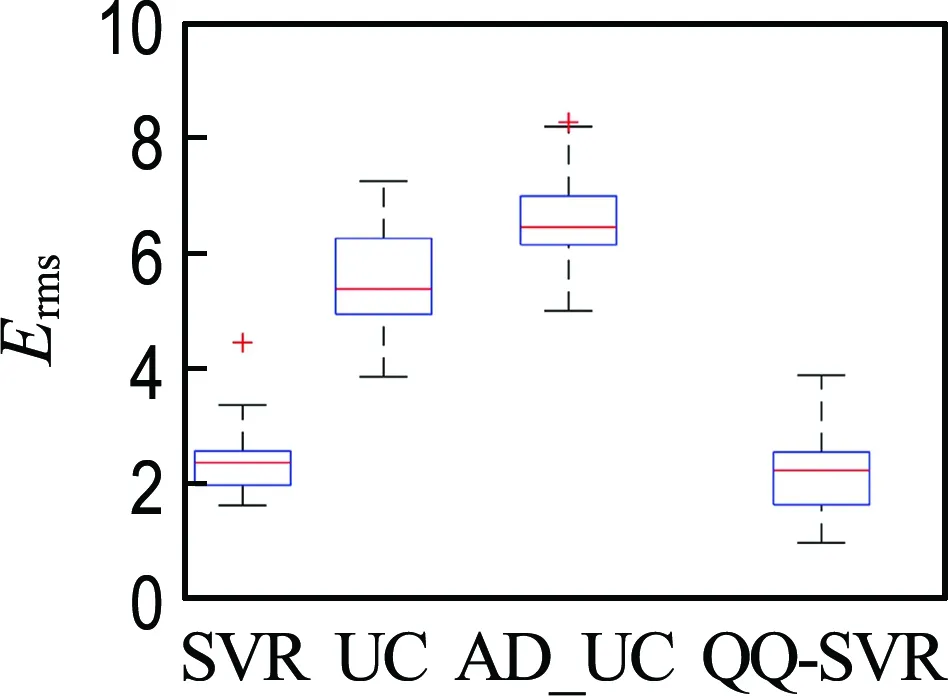

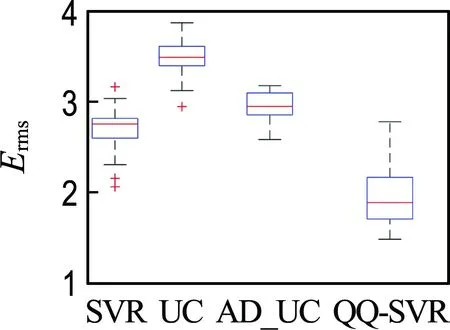



3 经典工程算例
3.1 弹簧设计



3.2 焊接梁设计



3.3 压力容器设计
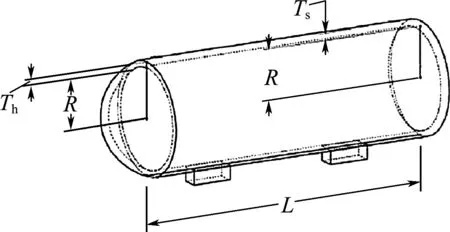

4 种植牙骨应力预测
4.1 问题描述
4.2 有限元模型


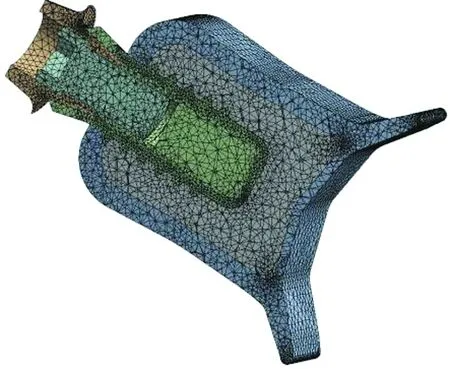
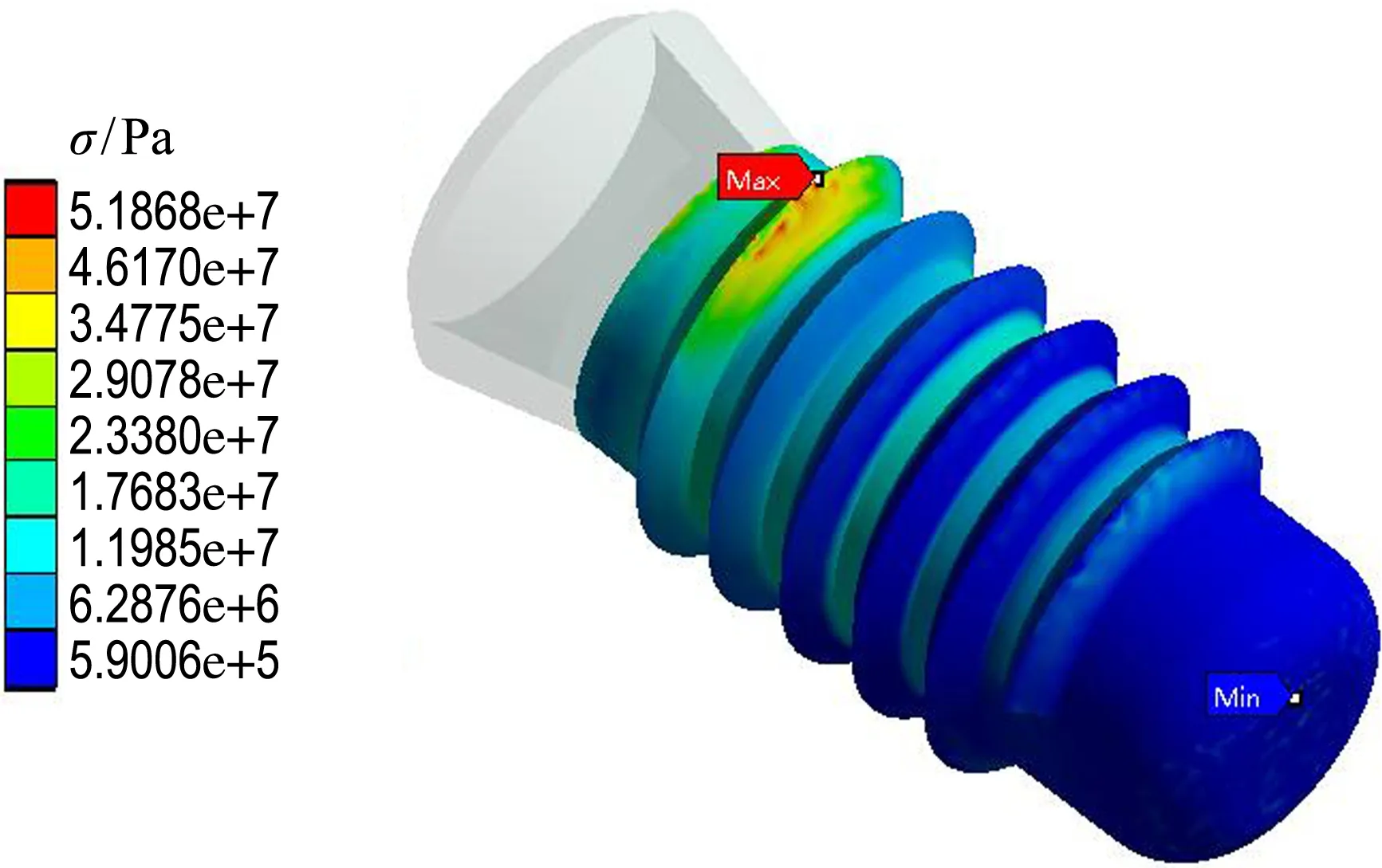
4.3 实验结果
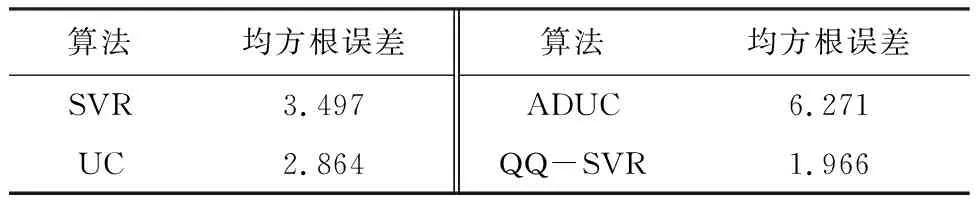
5 结 语

