解信赖域子问题的多折线算法

申理精 ，郭栋栋，王希云

(1.太原科技大学 应科学院，太原 030024；2.山西应用科技学院，太原 030024)

求解无约束优化问题

(1)

的信赖域方法的基本思想是在当前迭代点x(k)的附近用一个二次函数逼近目标函数f，用该二次函数在x(k)的领域内的极小值点作为下一个迭代点[1-4]，该二次函数为：

s.t.‖δ‖≤Δk

(2)

称为信赖域子问题，其中δ=x-x(k)，Bk∈Rn×n是f在x(k)的Hessian阵或其近似，参数Δk>0，则

x(k+1)=x(k)+δ(k)

随着参数Δ的变化，问题(2)的解δ*在空间留下一条曲线称为最优曲线[5-6]，Δ称为信赖域半径。

在Hessian阵正定的条件下，关于子问题(2)的求解，文献[7-13]给出了不同的折线算法，文献[14]构造了双割线折线算法，本文基于双割线折线法构造了多折线算法，通过几何图形，得到多折线算法比割线法求解子问题时更精确，分析了多折线算法的收敛性，通过数值试验与双割线折线法[12]进行比较知新算法更好。

1 折线的构造

B正定时，最优曲线方程为：

δk=-(B+μI)-1g，其中μ≥0

(3)

点δap的切线方向与δnp方向平行[14]，因点δap的切线方向δnp=-B-1g平行，

因此由

d/dμ[-(B+μI)-1g]=B-1g，

即

(B+μI)-1(B+μI)-1g=B-1g，

有Ig=(B+μI)2B-1g，两边左乘B，

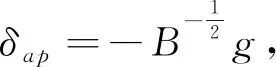
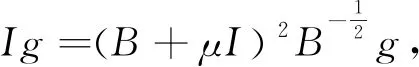
δrp=

(4)

λi是B的特征值。

连接初始点θ，δrp，δap，δnp形成一条多折线路径，在图1中可见，新路径记为Γ3=[θ，δrp，δap，δnp].

图1 折线路径图

其中Γ1=[θ，δzp，δnp]是切线单折线[12]，Γ2=[θ，δap，δnp]是双割线折线[14]，Γ3=[θ，δrp，δap，δnp]为本文算法路径，从图1可看出，本文所得的多折线法路径更接近最优曲线。

2 算法

步1：给定梯度g，正定阵B，Δ；

步3：计算δnp：δnp=-B-1g；

步4：Γ3=[θ，δrp，δap，δnp]；

步5：确定子问题(2)的解

当‖δrp‖2≤Δ≤‖δap‖2，则

δk=δrp+η(δap-δrp)，其中η满足‖δk‖2=Δ；

当‖δap‖2≤Δ≤‖δnp‖2，则δk=δap+η(δnp-δap)，其中η满足‖δk‖2=Δ；

当Δ≥‖δnp‖2，则δk=δnp.

3 收敛性分析

定理1解子问题(2)时，多折线路径满足：

点x从点xk出发沿多折线路径向前行进时，

I：‖x-xk‖=‖δ(τ)‖2单调增；

II：函数值qk(δ(τ))严格单调减。

记多折线为δ(τ)，则：

(5)

要求δ(τ)满足I和II.

证明：0≤τ≤1时，

II：记φ2(α)=qk(δ(α))，α∈(0，1)

当‖B‖2<1时，

对B做谱分解：B=UΤΛU，令g=Uy，z=U2y，则：

当‖B‖2≥1时，

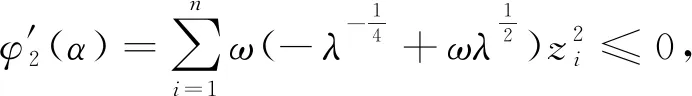
1≤τ≤2时， I：记：

当‖B‖2<1时，

对B做谱分解：B=UΤΛU，令g=Uy，

当‖B‖2≥1时，

对B做谱分解：B=UΤΛU，令g=Uy，z=U2y，则：

II：记h2(α)=qk(δ(1+α))，α∈(0，1)

h2(α)=qk(δrp+α(δap-δrp))=

α(δap-δrp)ΤB(δap-δrp)≤

(δap-δrp)Τ(g+Bδrp)+(δap-δrp)ΤB(δap-δrp)=

当‖B‖2<1时，

当‖B‖2≥1时，

所以1≤τ≤2时，满足I、II；

2≤τ≤3时，

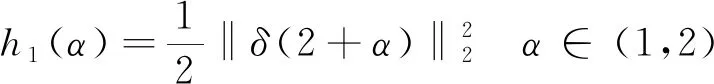
当‖B‖2<1时，

对B做谱分解：B=UΤΛU，令g=Uy，z=U2y，则：

当‖B‖2≥1时，

对B做谱分解：B=UΤΛU，令g=Uy，z=U2y，则：

再证II：记h2(α)=qk(δ(2+α))，α∈(1，2)

h2(α)=qk(δap+α(δnp-δap))=

gΤδap+αgΤ(δnp-δap)+

α(δnp-δap)ΤB(δnp-δap)≤

(δnp-δap)Τ(g+Bδap)+

(δnp-δap)ΤB(δnp-δap)=

当‖B‖2<1时，

=0

当‖B‖2≥1时，

=0

所以当2≤τ≤3时，满足I、II；

综上所述τ[0,3],δ(τ)满足I、II，证毕。

4 数值试验

采用测试函数1与测试函数2对多折线算法进行数值试验[15-16]，同时与DSD算法[14]的数值结果进行比较见表1与表2，表中的Δ为信赖域半径，表中的qDSD-q本文算法指本文的多折线算法与DSD算法的最优值差。

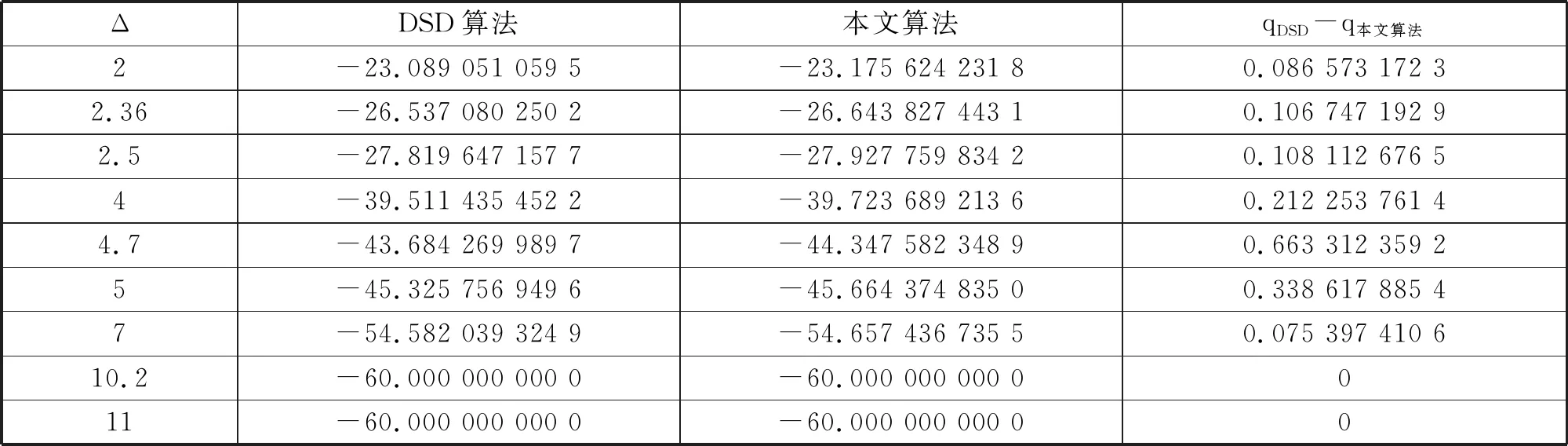
表1 测试函数1数值结果比较表

表2 测试函数2数值结果比较表

测试函数1：

s.t.‖δ‖2≤Δ

测试函数2：

s.t.‖δ‖2≤Δ

由表1与表2的数值结果比较可得出：本文构造的多折线算法无论对测试函数1还是测试函数2当信赖域半径的取值小于10.2时其数值表现都优于算法的数值表现，当信赖域半径取10.2与11时多折线算法与算法表现相当。

因此针对信赖域子问题的求解，本文用多折线来逼近最优曲线，无论是从几何上分析还是从数值试验的表现上都说明本文算法是有效的。